TBM掘進總推進力關鍵參數識別與高精度Kriging模型

李 杰，王林濤，孫 偉，欒鵬龍

（大連理工大學機械工程學院，遼寧 大連 610024）

1 引言

TBM掘進載荷包括總推進力和刀盤扭矩，其中推進力的值對掘進穩定性、破巖過程、施工安全等方面有直接影響。TBM在掘進過程中的總推進力多方面的影響，包括裝備的結構、施工時所處的地質條件，以及掘進過程中的運行參數。圍繞TBM掘進總推進力的問題，研究者做了大量的研究，最初由文獻1]給出了盾構推進力的經驗估計公式（推力F=βD2，β為經驗系數，D為直徑）被用于推進力的預測，其公式中直接顯示了裝備尺寸刀盤直徑對推進力的影響；文獻[2]通過巖石切割實驗，對刀盤刀具破巖過程中的應力做了進一步研究。接著，文獻[3-4]從刀盤結構變化的模擬試驗中，分析了刀盤開口率的變化對掘進載荷的影響，上述從經驗方法、破巖過程、結構變化的角度來研究載荷預測，有利于對TBM的設計和分析。在數值研究方面，文獻[5]分析了盾構掘進扭矩和轉速參數之間的作用關系，并取得較好的結果。文獻[6]分析了TBM掘進貫入參數和巖石特性之間的實測數據庫，建立了掘進貫入度預測模型；文獻[7]對工程實測數據進行總推進力的分析，建立掘進總推進力的力學模型。文獻[8]采用遺傳算法，改進了TBM掘進刀盤的布局，進一步提高掘進效率。此外，在對TBM掘進總推進力建立模型中，參數的選擇一般采用排隊論[9]來實現模型的建立。然而，TBM在掘進過程中，條件復雜，導致識別對推進力有影響的關鍵參數和建立高精度預測模型是困難的。

隨著數據時代的進一步發展，大數據挖掘數據之間關系的技術，為復雜系統建模和參數的識別提供新的思路[10]。從TBM掘進數據中識別對掘進總推進力有影響的關鍵參數，提高推進力預測模型精度是主要目的。在分析工程實測數據的基礎上，利用Kriging模型識別對總推進力有影響的關鍵參數，提高總推進力的預測模型精度，并結合引松工程現場所記錄的實測數據討論該方法的有效性。

2 參數識別和Kriging模型技術路線

通過對引松工程的實測數據分析，采用Kriging模型參數識別影響TBM掘進總推進力的關鍵參數，并建立高精度的Kriging推進力預測模型，其技術路線圖，如圖1所示。

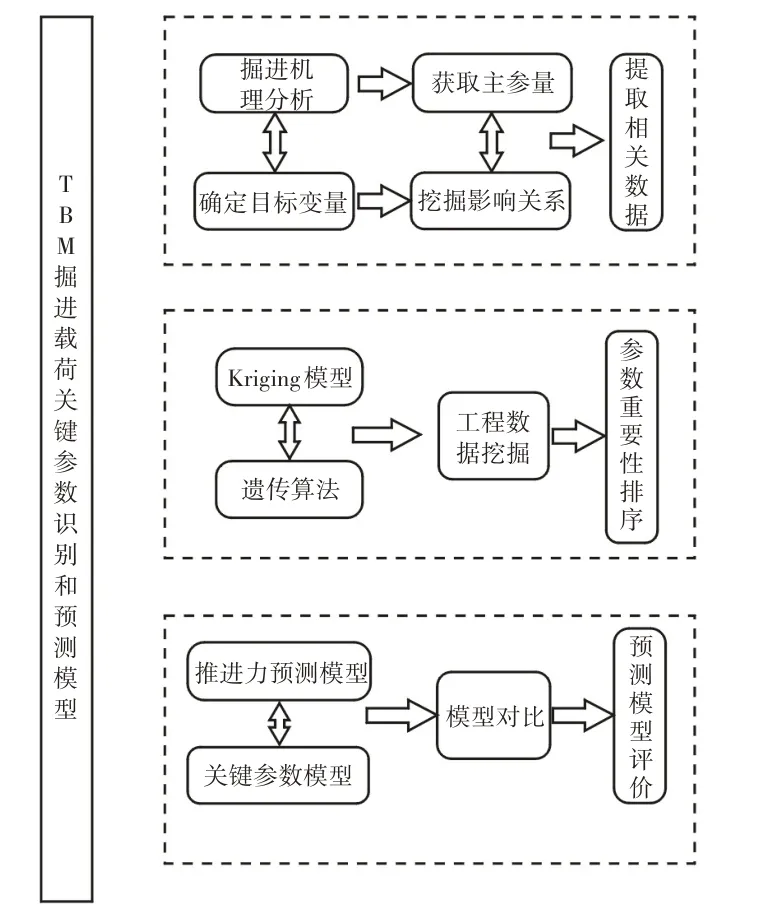
圖1 推進力參數識別和建立模型技術路線Fig.1 Identify Thrust Parameters and Bulid Model Technical Route

3 TBM掘進總推進力和掘進參數分析

對于敞開式TBM，TBM掘進時所需要的推進力為刀盤推力及TBM與洞壁、內外大梁之間摩擦力等之和[11]，如式（1）所示。

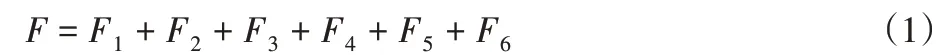
式中：F1—掘進時刀盤各刀具作用在掌子面上沿洞軸線方向的分力之和；F2—掘進時刀盤下部浮動支撐與洞壁之間的滑動摩擦力；F3—頂護盾與洞壁之間的摩擦力；F4—刀盤側支撐與洞壁之間滑動摩擦力；F5—大梁水平導軌間滑動摩擦力；F6—掘進時隨刀盤向前移動部分的后配套對機器的拖動阻力。

分析TBM掘進過程有關影響掘進載荷因素，當TBM在掘進過程中的載荷很大程度是由運行過程參數所反映[12]，例如，掘進姿態可以通過運行參數反映，掘進過程中俯仰角，滾動角等運行參數。因此TBM在掘進過程中由傳感器采集的包括貫入度（λ）、刀盤轉速（v c）、推進速度（v s）等掘進參數，對引松工程項目的開敞式TBM進行研究，選取實際施工過程中地質類型為相同類的相關數據。結合上述分析方法，確定有關影響推進力的參數有21個，如表1所示。目標變量為總推進力。

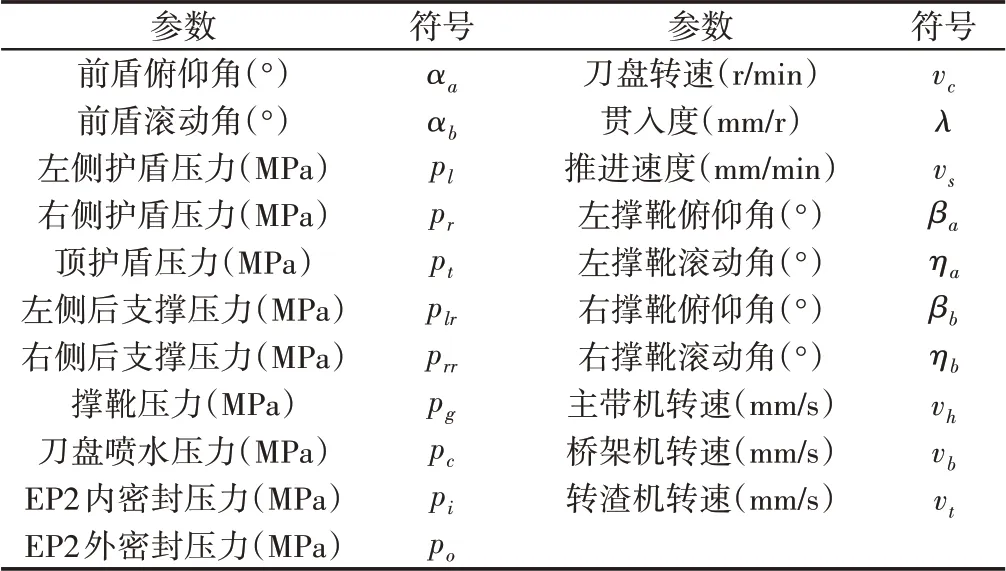
表1 參數變量Tab.1 Parameters Variables

4 Kriging模型的關鍵參數識別方法

Kriging模型的關鍵參數識別方法通過樣本點與已知樣本之間的差異大小來衡量參數與目標變量之間的相關性，適合多變量、多參數的分析，可有效識別影響TBM總推進力預測的關鍵影響參數，確定TBM掘進總推進力模型的參數輸入。因此，Kriging模型識別TBM掘進總推進力預測關鍵參數，從而提升TBM掘進總推進力模型預測精度。

4.1 Kriging模型的原理和參數識別原理

Kriging模型的函數表達式為下式：

式中：x—已知樣本點的數據；y(x)—未知樣本點的函數值；f j(x)—已知的近似函數；βj—它的系數；z(x)—隨機高斯過程函數，其均值為0，方差為σ2。

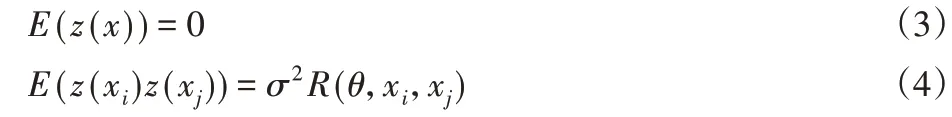
式中：R(θ，x i，x j)是關于x i和x j的相關函數，θ相關系數，是未知參數θi的集合。

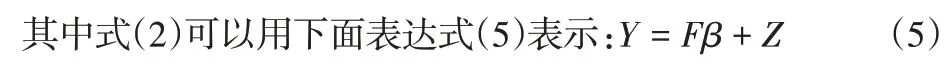
假設所建立的模型沒有偏差，并且已知的擬合函數對已知點的擬合完全正確，響應來自高斯分布，則Y-Fβ服從多維元正態分布，記為：Y-Fβ～N(0，∑)，其中∑=σ2Rθ，參數σ2和β是使用最大似然估計（MLE）獲得的，對應的似然函數并取對數，根據對數似然函數，分別對σ2和β求導，并將其導數置于零，可得σ2，并得到對數似然函數（7）：

參數θi（θi>0）通過最大化上式（7）通過遺傳優化算法（GA）多次迭代得到滿足適應條件的最優解［13］。

其Kriging中所用的R(θ，x i，x j)相關函數一般為徑向基函數組成的相關矩陣組成。

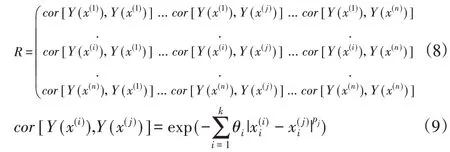
式中：k—參數的個數；p j—參數，p j=2。

通過對遺傳算法最大化式（11），設置參數θi的上下界，從而確定使式（9）取得最大化時的參數θi。參數θi衡量對應輸入參數的重要性，如圖2所示。

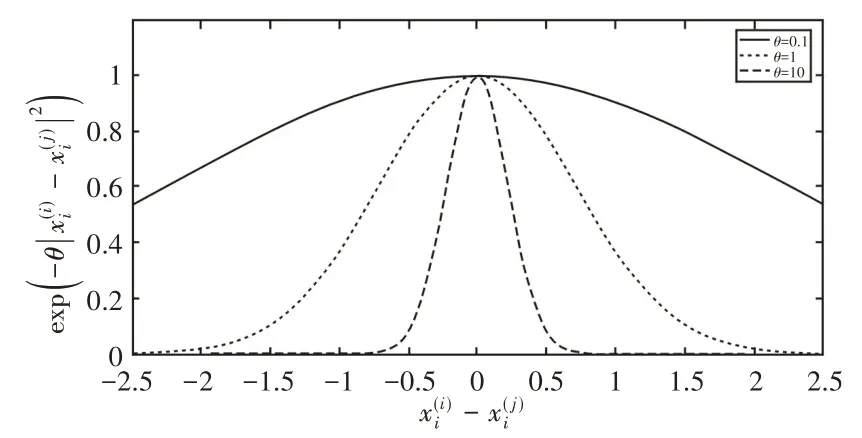
圖2隨θ變化參數相關性Fig.2 Correlations with Varyingθ

θ對相關性的影響，當θ值較低時，表明Y(x(j))跟樣本點有很高的相關性，與已知的樣本相似，然而當θ值較高時，表明Y(x(j))之間存在顯著差異，因此考慮用θi視為衡量所接近的函數的“活躍度”的指標，如圖2所示。即當θi的值較低時，表明其對應的參數對函數影響作用小，當θi值較大時，由于其與已知樣本點有較大差異，表明其對應的參數對函數影響大。

4.2實測數據關鍵參數識別

為了在Kriging模型算法中更好的進行數據的運算，將原始數據變化到［0，1］區間，變換公式，如式（10）所示。

式中：x n—歸一化得訓練集和測試集數據；x i—原始測試集和訓練集數據；xmax、xmin—訓練集和測試集的最大值和最小值。

根據上述識別方法，確定用來確定識別關鍵參數的樣本數據大小為290，變量個數為21個，目標變量為總推進力，進行總推進力關鍵參數識別。由上述式（9）進行遺傳優化算法進行求解，其θ?[10-3，102]，確定對應的θ，其各參數所對應的θi進行權重占比計算，其中θ權重占比的計算公式，如式（11）所示；各參數所對應的參數權重，如圖3所示。

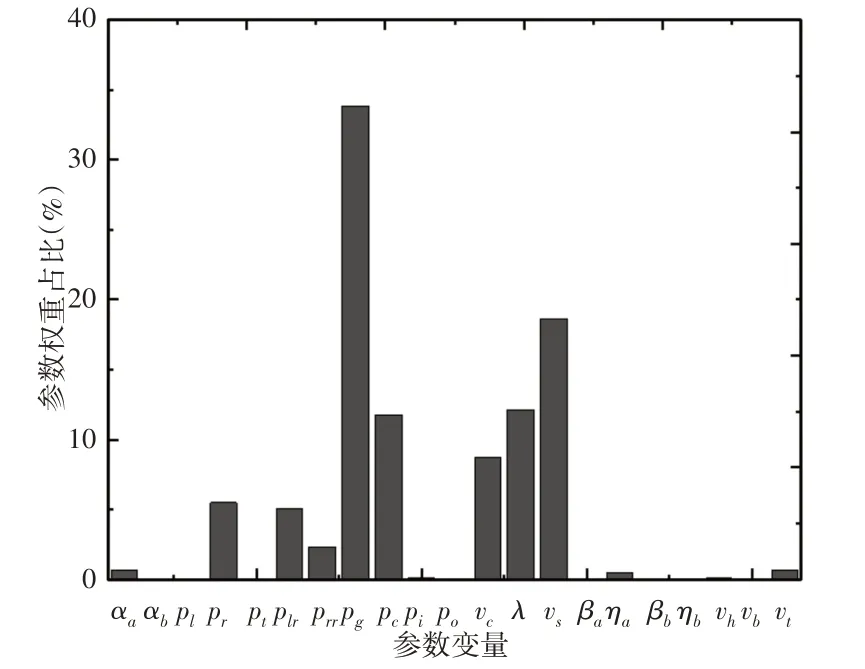
圖3參數權重占比圖Fig.3 Parameter Weight Proportion

式中：k—推進力有關參數的個數。

根據大量試驗，當參數權重占比大于5%時，對應參數對推進力有主要影響，當參數權重占比小于1%時，對應參數對推進力幾乎沒有影響。權重占比越大，對推進力影響越大。

由圖3參數變量權重占比分析可知：

關鍵參數影響順序：撐靴壓力（p g）>推進速度（v s）>貫入度（λ）>刀盤噴水壓力（p c）>盤轉速檢測值（v c）>右側護盾壓力（p r）>左側后支撐壓力（p lr）>右側后支撐壓力（p rr）

綜上可知，對TBM掘進總推進力有主要影響的參數個數為8個，其余13個參數影響小。

5掘進總推進力模型驗證和討論

5.1模型評價標準

對于建立的推進力模模型性能進行評價，所采用的評價準則相關系數（R2），其表達式，如式（12）所示。

5.2建立Kriging推進力預測模型對比

確定TBM掘進總推進力模型的輸入參數，對模型的輸入參數個數不同所建立對用不同的Kriging模型，根據引松工程所記錄的數據，樣本大小為1200，其中75%的樣本為訓練集和25%的樣本為測試集。分別建立了21個變量所對應的Kriging推進力模型和8個關鍵參數變量所對應的Kriging推進力模型，其預測精度，如圖4、圖5所示。由圖4和圖5可知：（1）21個參數所建立的模型精度R2=0.68（2）8個主要參數所建立的推進力模型精度R2=0.81，顯示相關度較高，表明模型預測值與工程實測數據非常接近，關鍵參數建立的推進力模型能較為準確地預估掘進載荷值。

圖4 21個變量推進力模型精度Fig.4 21 Variable the Thrust Model Accuracy

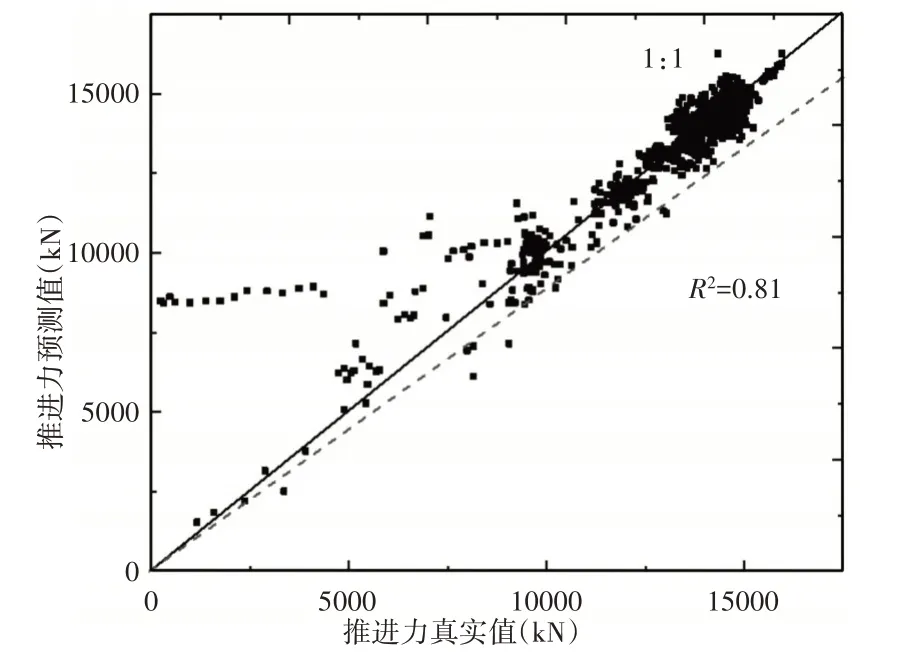
圖5 8個關鍵變量推進力模型精度Fig.5 8 Key Variables Thrust Model Accuracy

6 結論

針對TBM掘進進總推力關鍵參數識別和Kriging推進力模型建立的研究，分析引松工程TBM掘進系統所記錄現場相關數據，識別對推進力有主要影響的關鍵參數，建立高精度Kriging推進力預測模型，得到以下結論。（1）Kriging模型的中參數系數分析是有效的關鍵參數識別方法，能夠挖掘實測數據樣本和目標變量中的作用規律，識別對總推進力有主要影響的關鍵參數。（2）結合引松工程實測數據，通過模型輸入參數占比比較，實現了對掘進參數影響大小進行排序，確定了其對應推進力有關參數的影響順序，識別了對推進力影響小的參數。（3）通過對比分析引松工程實測數據中的總推進力數值與其關鍵參數所構建的高精度Kriging推進力模型預測值，有效的驗證了該模型能預估總推力載荷值，進一步也驗證了對關鍵參數可以實現構建高精度的Kriging推進力模型。