主動諧波消除多電平射頻脈寬調制策略及其性能分析
陳劍斌,周 強,朱 蕾,張 江
(1. 陸軍工程大學 通信工程學院, 江蘇 南京 210007; 2. 國防科技大學 第六十三研究所, 江蘇 南京 210007)
隨著當前無線通信業務類型的快速增長,通信終端在小型化的同時需要兼容更多的功能和標準,從而在帶寬、效率以及可重配置性等方面都面臨更高的要求和挑戰。傳統模擬體制發信機中模擬射頻器件參數固定,且效率、線性和帶寬等主要性能指標在理論上相互制約[1],從而極大制約了發信機的效率、體積以及可重配置等性能。軟件定義無線電(Software Defined Radio,SDR)[2]采用數字信號處理技術完成傳統模擬器件功能,可以實現對不同通信業務的適配,因此得到越來越多關注。其中,全數字發信機(All-Digital Transmitter,ADTx)[3]技術在數字域完成上變頻和功率放大等射頻功能,具有靈活的可重構和可編程性能,被認為是實現SDR系統的理想方案。
ADTx如圖1所示,主要包含數字射頻調制器、開關模式功放(Switched-Mode Power Amplifier,SMPA)以及調諧濾波器[4-6],其中數字射頻調制器完成基帶信號的上變頻和脈沖編碼,生成脈沖序列以驅動后級SMPA實現高效放大。由于脈沖編碼降低幅度分辨率,引入大量量化噪聲,為保證輸出信噪比和頻譜純度,需引入噪聲整形技術,將帶內量化噪聲轉換為帶外噪聲或諧波。因此基于噪聲整形的脈沖編碼算法不僅決定ADTx輸出信號質量,而且直接影響后級SMPA工作效率,是ADTx實現高效率和高線性的核心。
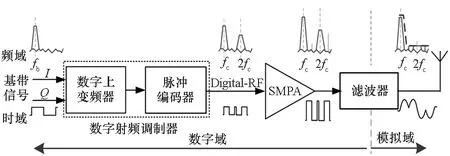
圖1 ADTx系統框圖Fig.1 Structure diagram of ADTx system
Delta-Sigma調制(Delta-Sigma Modulation,DSM)[7-8]和脈沖寬度調制(Pulse-Width Modulation,PWM)[9-11]是目前ADTx系統主要的脈沖編碼技術。其中DSM能夠實現更高的帶內信噪比,但其硬件實現復雜度較高,且輸出脈沖序列的切換頻率數倍于載波頻率,從而大大增加后級功放損耗[7]。同時,DSM輸出脈沖序列在信號帶外存在大量噪聲,需要采用高Q值帶通濾波器抑制,增加了系統實現難度。在傳統PWM基礎上,Raab提出射頻脈寬調制(Radio Frequency Pulse Width Modulation,RF-PWM)技術[9]。相較于DSM,RF-PWM可以有效降低設計復雜度,且其輸出脈沖序列切換頻率僅為射頻載波頻率的2倍,可以有效減少功放損耗。此外,RF-PWM量化噪聲體現為諧波分量,采用低通濾波即可實現信號恢復。因此,RF-PWM被認為是目前最適合ADTx的脈沖編碼算法。
另一方面,在實際系統應用中,由于RF-PWM輸出脈沖序列存在的大量諧波分量不僅影響編碼效率,在寬頻段應用下還對調諧濾波器設計提出較高挑戰。通過增加輸出脈沖序列電平數,多電平RF-PWM方案[12-14]在提升編碼效率的同時,可在一定程度上降低諧波幅度,但仍需引入高Q值濾波器。為降低系統輸出濾波要求,文獻[15]提出將單個脈沖分解為多個窄脈沖的方案實現對諧波分量的抑制。但受采樣頻率以及實際硬件電路非理想特性制約,該方案僅適用于基帶PWM。文獻[16]提出了一種基于固定門限的多電平RF-PWM方案,實現對輸出脈沖序列特定諧波的消除,但僅適用于恒包絡信號。針對非恒包絡信號,文獻[17]提出了一種基于自適應門限與RF信號比較的多電平RF-PWM方案,實現非恒包絡信號下特定諧波的主動消除。在文獻[16-17]基礎上,本文從諧波消除條件下各子脈沖序列的脈沖寬度要求出發,利用脈寬與信號幅度以及比較門限的關系,公式推導了基于3次諧波消除的5電平RF-PWM實現方案。同時根據方案中存在的基波分量與信號幅度間的增益變量,分析驗證了諧波抑制條件下的最佳增益系數。
1 固定門限比較RF-PWM
傳統的RF-PWM方案[9]通過將已調射頻信號與特定參考信號進行比較,得到一個與載波同頻且幅度固定而脈沖寬度可變的脈沖序列,其中原始調制射頻信號的幅度和相位信息分別對應于RF-PWM脈沖的寬度和延時。由于該方案采用變化的比較參考電壓,在高采樣率條件下硬件實現難度較高。為降低開關頻率且易于實現,可通過對輸入已調射頻信號進行預處理后再與固定的門限電平進行比較以產生最終的RF-PWM信號[11]。
固定門限比較RF-PWM輸出脈沖波形的情況如圖2所示。考慮輸入為歸一化的已調射頻信號Sin(t)=a(t)cos(2πfct+φ(t)),a(t)和φ(t)分別為歸一化的包絡和相位信號,且有0≤a(t)≤1。則脈沖序列SPWM(t)可通過Sin(t)和比較門限電平Vth及-Vth的交點來定義。
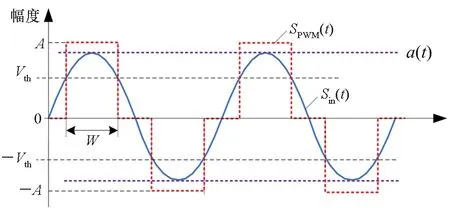
圖2 固定門限比較RF-PWM輸出脈沖波形產生示意圖Fig.2 Sketch map of RF-PWM pulses with fixed-comparison-threshold
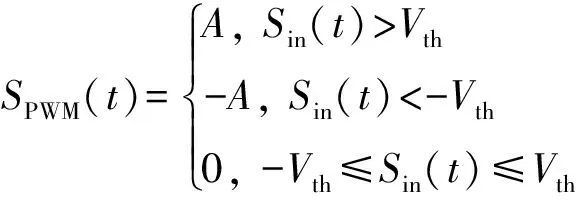
(1)
其中,A為調制器輸出幅度,為便于分析后文令A=1。假設滿足載波頻率遠大于包絡信號的a(t)帶寬,則在一定射頻周期內a(t)可近似為恒定值,對應周期內Sin(t)可看作正弦信號。利用部分傅里葉級數分析方法[18],SPWM(t)可表示為:
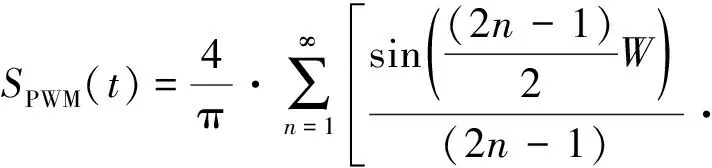
(2)
其中,ωc=2πfc,n為正整數,W為脈沖寬度。
(3)
考慮到SPWM(t)具有半波對稱性,僅含奇次諧波,則由式(2)可得對應的第n次諧波幅值An。
(4)
根據式(3)和式(4)可得SPWM(t)的基波分量幅度為:
(5)
式(5)同時也是非恒包絡信號下固定門限比較RF-PWM的AM-AM傳遞函數。為保證RF-PWM最終實現線性輸出,A1與a(t)需為正比關系。基于此,固定門限電平比較策略在保持門限Vth固定的同時引入預失真技術對基帶信號幅度a(t)進行預處理。定義預處理后的幅度為:
(6)
由式(5)~(6)可知,此時A1= 4A/π·a(t),其中4A/π為調制器增益。由于a(t)不能為1,因此a(t)的動態范圍將受限,推薦其最大值在0.9~0.95范圍內[11]。
為提升脈沖編碼性能,可以通過增加比較門限數量以提升輸出脈沖電平,對應M電平脈沖序列SML-PWM(t)的第n次諧波幅值An_ML為:
(7)
其中,K=(M-1)/2。則M電平RF-PWM的AM-AM傳遞函數為:
(8)
K>1時,式(8)的反函數難以獲得解析表達式,此時可通過軟件預先計算后采用存儲查表的方式獲取用于幅度校正的預失真幅度值。
2 主動諧波消除RF-PWM策略
2.1 策略基本原理
已有固定門限多電平RF-PWM方案通過引入多個比較門限并對a(t)進行式(8)所示的預失真校正,可以確保多個子脈沖波形的基波分量之和A1_ML與a(t)成正比。通過進一步增加量化電平,可以一定程度實現RF-PWM輸出脈沖序列高次諧波分量抑制,但抑制效果有限[16]。注意到式(7)所示的脈沖寬度與諧波幅度的關系,考慮通過控制各個子脈沖的寬度,以實現對特定諧波分量的主動消除。
假設需要消除L個不同次的諧波分量,如X1次、…、Xj次、…、XL次,其中L為正整數且1≤j≤L。根據K個子脈沖基波分量疊加之和正比于a(t),以及L個奇次諧波分量加權之和為零的思路,可得到K個自適應門限的解析公式。基于上述方法,利用K個自適應門限最多可實現K-1個奇次諧波的主動消除[17]。另一方面,為降低輸出濾波的要求,應優先選擇消除離載頻最近的諧波。因此,下文將以3次諧波消除為例,給出對應RF-PWM的具體實現方案。
2.2 次諧波消除RF-PWM實現方案
根據前面的分析,要實現3次諧波消除,至少需要2個自適應門限。另一方面,增加門限數量會使對應解析計算變得困難,同時RF-PWM輸出電平數量增加也提升了后級SMPA電路實現的復雜度。因此,下面分析采用2個自適應門限來實現3次諧波抑制,此時對應兩個3電平子脈沖序列組合生成5電平PWM,如圖3所示。其中,Vth2≥Vth1。則根據前面的分析有:
(9)
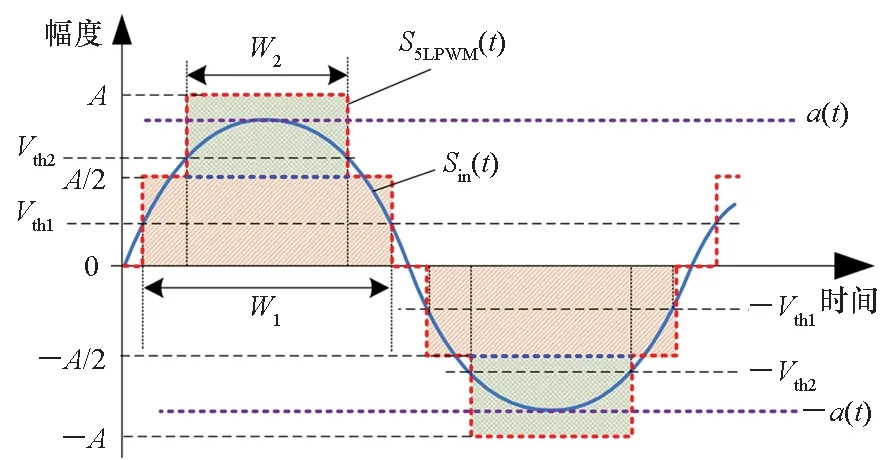
圖3 5電平RF-PWM波形產生示意圖Fig.3 Sketch map of 5-level RF-PWM
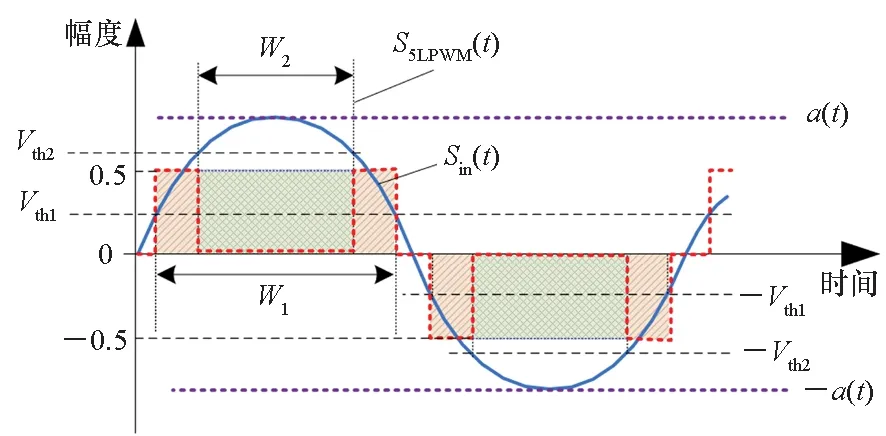
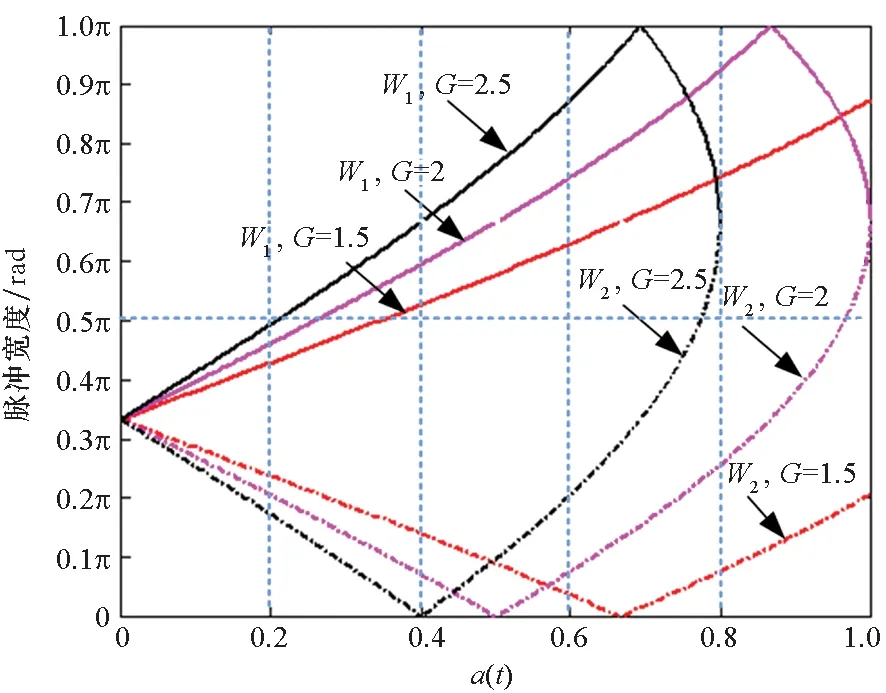
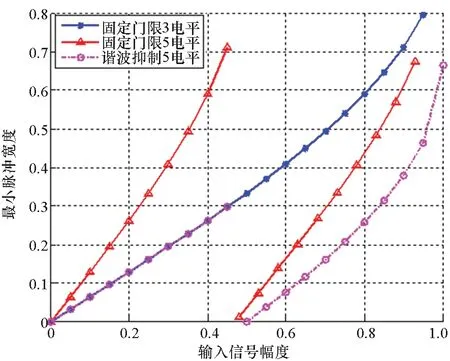
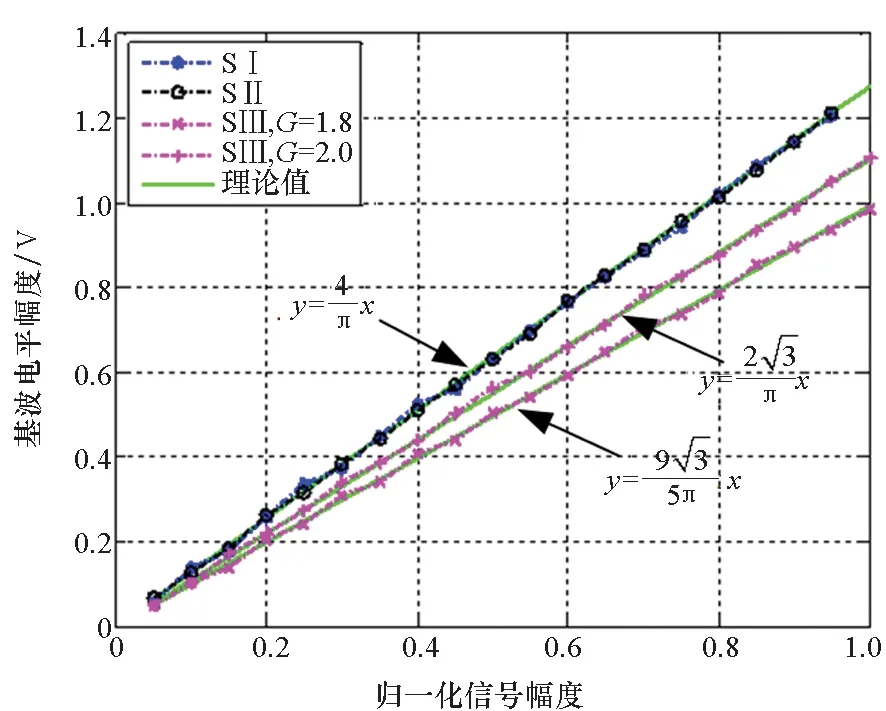
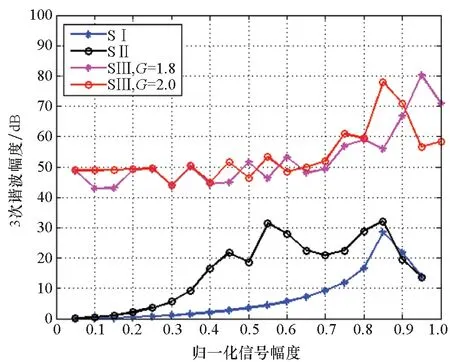
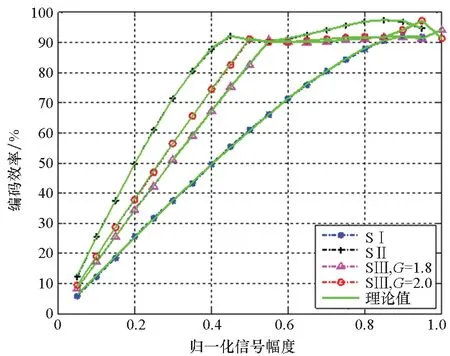
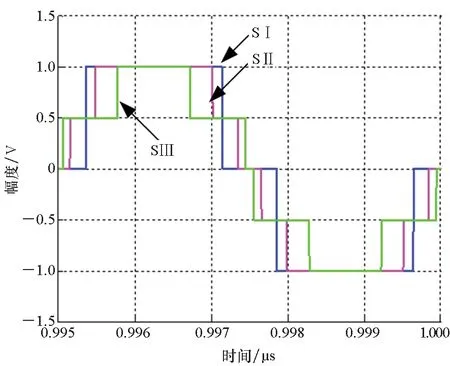
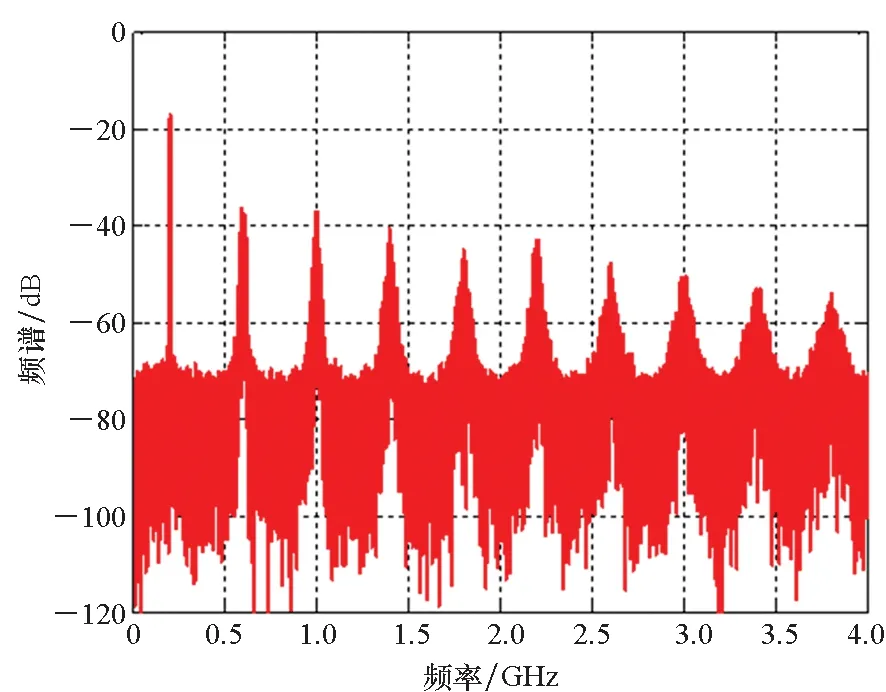
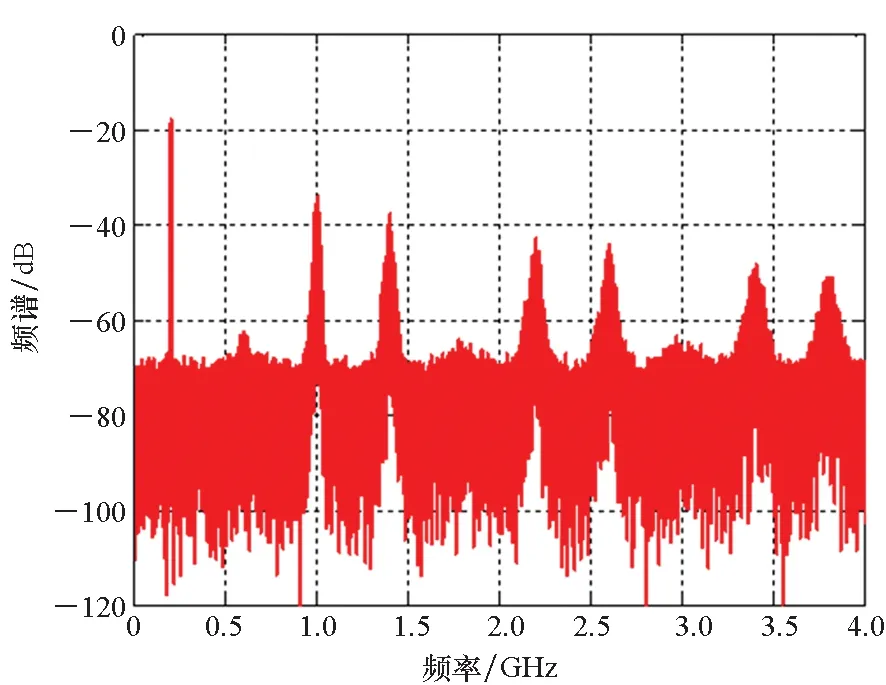
為確保策略的硬件可實現性,調制器增益g有限定的取值范圍,且具體取值與策略調制性能直接相關,下文將進行具體說明。另外,考慮到0 W1+W2=0 (10) 或 (11) 或 (12) 對于W1+W2=0,此時A1_5L=A3_5L=0,不滿足3次諧波消除RF-PWM策略的設計要求。當W1+W2≠0,將式(10)~(12)代入式(9),可以得到基波幅度為: (13) 進一步根據式(3)中門限與脈寬之間的關系可得: (14) 進一步根據式(3)還可得: (15) 另一方面,根據上述推導過程中脈沖寬度W1和W2各自的取值范圍以及兩者之間需滿足的限定關系,可以得到1/G≤a(t)≤2/G。當a(t)<1/G時,聯立式(10)~(11)對應的方程無解,說明此時滿足3次諧波消除條件的2個子脈沖波形之和的基波分量無法與輸入信號幅度保持正比關系。為解決這一問題,當a(t)<1/G時,采用2個子脈沖波形差來實現對3次諧波的消除,同時保證對應的基波幅度與a(t)的線性關系,如圖4所示。 圖4 5電平RF-PWM波形產生示意圖(a(t)<1/G)Fig.4 Sketch map of 5-level RF-PWM(a(t)<1/G) 此時為實現3次諧波消除,脈沖寬度應滿足: (16) 對應基波幅度為: (17) 根據門限與脈寬之間的關系,最終可以得到: (18) (19) 根據當前輸入采樣時刻RF信號的輸入幅度,生成如式(18)~(19)所示的比較門限,并按式(1)執行比較操作,即可生成3次諧波抑制的5電平RF-PWM序列。此外,考慮到正余弦函數的周期性,若sinθ=0或cosθ=0,且x為奇數(輸出脈沖僅含奇次諧波),則對應有sin(xθ)=0或cos(xθ)=0,因此根據式(9),容易驗證所提方案還可以消除特定次諧波的所有奇數倍諧波。 根據2.2節分析可知,主動諧波抑制方案應首先保證12-3G2a(t)2≥0。為使上述條件在所有幅度取值范圍內成立,可得增益系數的取值范圍為0 為進一步理解上述范圍的含義,基于式(18)~(19),利用式(3)可以得到對應的兩個子脈沖寬度W1和W2與輸入信號幅度之間的關系: (20) (21) 增益系數分別為1.5,2.0,2.5時對應的關系曲線如圖5所示。從圖5中可以看出,當增益系數為2.5時,幅度a(t)>2/G=0.8時,對應脈沖寬度W1和W2無實數解。說明在此范圍內,滿足諧波抑制條件的RF-PWM脈沖序列基波幅度與信號幅度無法滿足線性關系,從而實際發送信號中將引入失真,且G越大,對應失真也越大。另一方面,注意到G=2時,恰好保證在幅度a(t)的全部取值范圍內都存在實數解。綜上所述,G≤2是3次諧波消除5電平RF-PWM實現的必要條件。下面進一步分析主動諧波抑制策略的調制性能。 圖5 不同增益系數下脈沖寬度與信號幅度的關系Fig.5 Correlation of pulse-width and amplitude for different gain index 除了諧波抑制,考慮到實際系統中存在的電路寄生電容會增大輸出脈沖的上升、下降延時,當包絡幅度較小即脈沖較窄時,將引起脈沖畸變甚至丟失,從而引入額外失真。因此最小脈沖寬度也是脈沖編碼算法需要關注的指標。首先根據圖5中子脈沖寬度W1和W2與輸入信號幅度a(t)之間的關系曲線,同時注意到當a(t)<1/G時最小子脈沖寬度為W1-W2,容易得到:增益系數G越小,對應的主動諧波抑制RF-PWM序列最小脈沖寬度也越小。因此從增大最小脈沖寬度的角度出發,最佳增益系數值應取2。 在最佳增益系數值下進一步分析主動諧波抑制RF-PWM方案與現有固定門限方案之間的最小脈沖寬度情況。根據不同方案下比較門限與輸入信號幅度的具體關系,進一步利用式(3)可以得到不同RF-PWM方案下的最小門限與輸入信號幅度關系,對應結果如圖6所示。其中,固定門限5電平RF-PWM預失真信號幅度由查表方式得到,對應的兩個比較門限電平分別為0.1和0.35。可以看到,相比現有固定門限RF-PWM,主動諧波抑制RF-PWM使得序列最小脈沖寬度減小,從而一定程度上加劇了信號失真。實際應用中為消除脈沖寬度壓縮的影響,可以引入相應的預失真方案來實現脈沖畸變的補償[19]。 圖6 最小脈沖寬度與輸入信號幅度理論關系曲線Fig.6 Theoretical curve for correlation of minimum-pulse-width and input-amplitude 另一方面,脈沖編碼算法的另一個重要指標是編碼效率,該指標直接影響ADTx系統的整體效率。編碼效率定義為實際發送RF信號功率PS與脈沖編碼序列功率PA之比[12]。 (22) 下面具體分析不同RF-PWM方案的編碼效率性能。對于現有固定門限電平方案,3電平下脈沖序列編碼效率為: (23) k為固定常數,代表仿真中基波電平到實際基波功率的變換系數。由于5電平下對應的子脈沖幅度寬度無法得到對應解析表達式,因此后文將結合仿真分析其編碼效率性能。另一方面,對于主動諧波抑制RF-PWM脈沖序列,根據不同幅度下子脈沖具體組合方式的不同,可以得到序列功率: (24) 結合理論分析,利用MATLAB軟件仿真驗證分析主動諧波抑制RF-PWM的性能。為進行對比,同時仿真固定比較門限RF-PWM策略。其中固定門限3電平為方案SⅠ,采用比較門限0.1。基于固定比較門限5電平RF-PWM為方案SⅡ,采用比較門限0.1和0.3。主動諧波抑制RF-PWM為方案SⅢ,并在仿真中分別令G=1.8/2.0,以驗證增益系數G對策略性能的影響。根據前面分析,具體仿真時,固定門限策略RF-PWM根據輸入信號幅度,先進行幅度預失真再執行比較操作,主動諧波抑制RF-PWM則是根據當前時刻幅度先確定兩個比較門限值,再執行比較。 (a) 基波幅度(a) Amplitude of based harmonic (b) 3次諧波功率(b) Power of 3rd harmonic (c) 3次諧波抑制 (c) 3rd harmonic suppression (d) 編碼效率(d) Coding efficiency圖7 單音輸入功率回退下的RF-PWM性能Fig.7 Performance of RF-PWM for back-off signal-tone input 圖7(b)、(c)給出了3次諧波抑制情況。通過增加量化電平,SⅡ相比于SⅠ,其3次諧波抑制性能有所提升,但提升僅限在一定輸入信號幅度范圍內(0.25≤a(t)≤0.85)。對于SⅢ方案,其3次諧波抑制能力在全范圍內顯著優于SⅠ和SⅡ,即使相比SⅡ也能夠獲得25~50 dB的性能提升,從而驗證了本文方案的有效性。同時注意到,不同增益系數下,3次諧波抑制性能基本相同。這主要是由于時域仿真分辨率受限,無法精確實現諧波抑制所需的理論脈沖寬度。 進一步對比各方案的編碼效率,如圖7(d)所示,圖7(d)中同時給出了相應的理論曲線。可以看到,理論值和仿真值基本吻合,同時得益于量化電平的增加,SⅡ和SⅢ的編碼效率均優于SⅠ。進一步對比SⅡ,雖然SⅢ輸出脈沖序列的總功率要小于SⅡ,但由于此時調制器增益和輸出脈沖基波功率的降低,其編碼效率反而要小于SⅡ。尤其是當信號幅度a(t)<1/G時,此時SⅢ退化為3電平,與SⅡ的序列功率差值減小,而兩者調制器增益差值恒定,使得此時編碼效率出現較大差距。此外,隨著增益系數G的降低,基波功率減小,對應SⅢ編碼效率性能下降。這進一步驗證了增益系數G的最佳值。 在非恒包絡復雜調制信號下對比不同方案的調制性能。采用峰均功率比(Peak to Average Power Ratio, PAPR)為6.35 dB,載波頻率為200 MHz,符號速率為5 Mbit/s的16 QAM信號作為RF-PWM的輸入信號,信號等效采樣頻率為20 GHz,SⅢ方案采用最優增益系數G=2.0。圖8分別給出了方案SⅠ,SⅡ和SⅢ下的脈沖序列時域波形及其對應的輸出頻譜。可以看到,在相同的輸入信號和仿真條件下,方案SⅠ下得到的調制信號具有最大的各次諧波。對于方案SⅡ,其各次諧波皆小于SⅠ。而SⅢ的3、9次等3x次諧波已基本被消除(與底噪基本平齊),因此離射頻信號最近的諧波為5次諧波。 (a) 時域波形(a) Time domain wave (b) SⅠ方案(b) Method of SⅠ (c) SⅡ方案(c) Method of SⅡ (d) SⅢ方案(d) Method of SⅢ圖8 16QAM輸入下不同方案的輸出特性Fig.8 Output feature for different pulse-coding methods with 16QAM input 表1給出了在相同輸入信號和仿真條件下,三種RF-PWM方案的性能對比。可以看出,SⅡ和SⅢ的主要性能指標,如編碼效率、諧波抑制、鄰信道功率比等,幾乎全面優于SⅠ。進一步對比兩種5電平方案,可以看到SⅢ的大部分指標和SⅡ相當,雖然在編碼效率等指標上略差于SⅡ,但SⅢ在諧波抑制上的明顯優勢將對濾波器的設計和實現提供有力支撐,從而有利于提高ADTx的綜合性能。 表1 16QAM信號輸入下不同脈沖編碼方案的性能對比Tab.1 Performance comparison for different pulse-coding methods with 16QAM input 通過對多個子脈沖序列的脈沖寬度進行控制,在確保子脈沖基波分量加權和與輸入RF調制信號幅度保持正比關系的同時,可以實現對特定諧波的消除。同時通過優先消除低次諧波,主動諧波抑制RF-PWM策略能夠有效降低ADTx系統對后級成型濾波器的設計要求,有利于提升寬頻段整體性能。 基于上述思想,以3x次諧波的主動消除為例,本文根據脈沖寬度與輸入信號幅度、比較門限之間的關系,推導了5電平RF-PWM的具體實現方案。在此基礎上,針對信號幅度與基波幅度的增益變量,分析了增益系數對諧波抑制方案的性能影響及其最優值,并通過性能仿真在驗證理論分析結果的同時證明了主動諧波消除RF-PWM策略的有效性。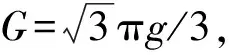
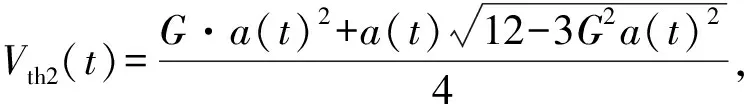
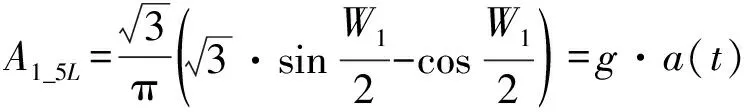
3 諧波消除RF-PWM性能分析
3.1 理論分析
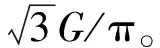
3.2 性能仿真驗證
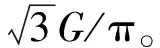



4 結論

