改進cell密度聚類算法在空戰目標分群中的應用
閆孟達,楊任農,王 新,左家亮,嵇慧明,尚金祥
(1. 空軍工程大學 空管領航學院, 陜西 西安 710051; 2. 中國人民解放軍94994部隊, 江蘇 南京 210019;3. 中國人民解放軍94701部隊, 安徽 安慶 246000; 4. 中國人民解放軍94347部隊, 遼寧 沈陽 110042)
空戰目標分群是態勢感知[1]階段的關鍵步驟,其目的在于根據當前空戰環境,綜合分析速度、航向和位置等態勢要素,將敵方參戰力量按一定的層次結構劃分為不同的空間群和相互作用群[2],幫助指揮員將紛繁復雜的目標信息規整為不同類型的目標群組,有助于減少冗余態勢信息,降低態勢評估難度,提高空戰決策準確度[3-4]。
目前,目標分群主要有兩大類方法。一類是基于相似性度量、優化算法和神經網絡的模型法。文獻[5-7]通過建立目標位置、航向等屬性的相似度函數,將相似度較大的目標劃分到同一群組。該方法雖然計算簡單,但需根據屬性的不同設置多種相似度調節系數和決斷閾值,實際應用效果不佳。文獻[8-10]分別利用蟻獅優化算法[11]、自組織特征映射(Self-Organizing Feature Mapping, SOM)神經網絡[12]、遺傳算法和支持向量機(Support Vector Machine, SVM)處理目標分群問題,這四種方法雖然實時性較好,但其穩定性相對較差且SOM和SVM的訓練數據難以獲得。另一類是對目標屬性進行聚類分析的屬性聚類法。文獻[13]首開基于聚類算法處理目標分群問題的先河,此后研究主要集中于如何使聚類算法更好地適用于目標分群問題。文獻[14-15]運用改進的K-means和模糊C均值聚類算法解決目標分群問題,上述算法只適用于編隊數目已知的聚類問題,雖然可以通過算法改進推理出可能的編隊數目,但其準確度相對較差。文獻[16-17]基于Chameleon算法處理目標分群問題,雖然該算法可處理類數未知問題且準確度較高,但其實時性相對較差。文獻[18]通過改進迭代自組織數據分析技術算法(Iterative Self-Organizing Data Analysis Techniques Algorithm, ISODATA)的分裂標準提高了分群效率,但該方法以歐式距離衡量目標相似度,只對球形分布數據有良好的聚類效果[19],而空中目標往往呈流形列隊,故該方法難以適用于目標分群。文獻[20-21]基于流形距離分別改進密度峰值算法和二階段聚類算法,使其能夠處理流形分布聚類問題,提高了目標分群的準確度,但流形距離計算復雜,容易造成實時性較差的問題。因此,發現一種能夠實現流形聚類,且實時性和準確度相對較好的聚類算法,是處理目標分群問題的關鍵。
基于cell的密度聚類(Cell-based Density Spatial Clustering of Applications with Noise, CBSCAN)算法[22]可以在事先不知道簇類數目的情況下,在含有噪聲點的數據集合中發現任意形狀的簇,對流形分布數據有較好的聚類效果。本文通過改進CBSCAN算法的簇類擴展方式,在保證算法準確度的同時,提高目標分群的實時性。
1 目標分群模型
目標分群是空戰態勢評估的首要任務。現代空戰中,敵方往往以多編隊協同空戰的方式向我方目標發起進攻,其主要編隊樣式為圖1所示的流形分布。若對敵方每架飛機逐一進行態勢評估,工作量很大且耗時較長。目標分群技術可以將編隊內部戰機劃分為一個整體,用對整體的評估預測代表對內部每架戰機的評估預測。
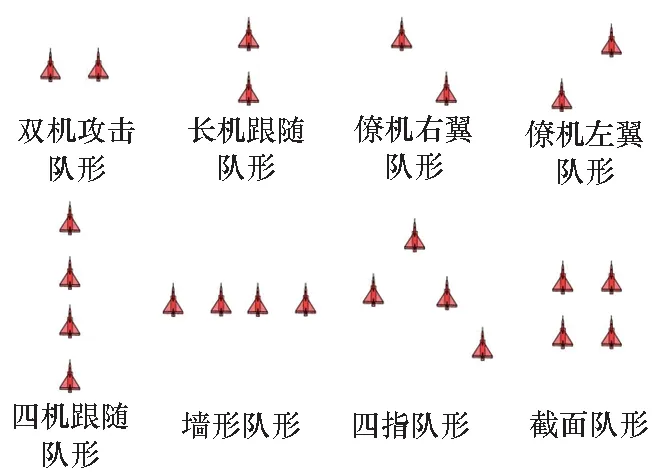
圖1 基本編隊隊形Fig.1 Basic formation style
1.1 分群類型
目標分群抽象層次如圖2所示,空戰目標分群是自底向上的分析推理過程,其主要分為:
1)空戰目標——參與空戰過程的作戰飛機(殲擊機、轟炸機等)及部分導彈。
2)空間群——空間位置相近且類型相同的空戰目標。
3)相互作用群——執行相同任務的空間群。
4)中立、敵、我方目標群——根據敵我屬性進行劃分后的相互作用群。
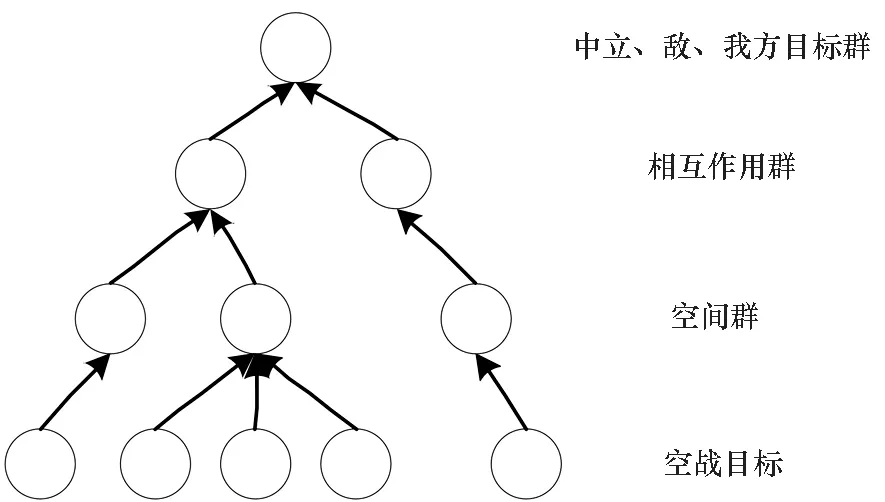
圖2 目標分群抽象層次Fig.2 Target grouping abstraction level
1.2 分群模型
令空戰目標數據集合為D={d1,d2,…,dn},其中di=(Fofi,Typei,xi,yi,θi,vi)(i=1,2,…,n)表示第i個空戰目標。目標各屬性參數如下所示。
Fof:空戰目標的敵我屬性。該參數可以由戰機上的敵我應答機自動判定,是進行目標分群的前提,只有當目標的Fof值一致時,才可將它們歸為一類。Fof=0表示目標為中立方目標;Fof=1表示目標為我方目標;Fof=2表示目標為敵方目標。
Type:作戰飛機類型,主要包括直升機、殲擊機、轟炸機等。不同類型的飛機一般執行不同的任務,處于不同的空間群。
{x,y}:作戰飛機的橫縱坐標。一般情況下,根據目標在xy平面上的分布即可將它們劃分到不同的空間群中。為節省時間開支將忽略目標的飛行高度數據,只根據橫縱坐標進行空間群劃分。
{θ,v}:作戰飛機的航向和速度值。由于航向和速度可以體現戰機執行任務的對象和任務類型,因此劃分空間群后,基于每個空間群的平均航向和速度,利用分群算法劃分相互作用群。
根據如圖3所示的模型框架,利用分群算法,最終可將探測到的空戰目標分為敵我識別群CC1、空間群CC2和相互作用群CC3。對于每種分群類型CCi,都包括多個群體Cj。例如CC3={C1,C2,…,Ck}表示將目標分成了k個不同的相互作用群。
在獲取空戰目標數據的基礎上,尋求一種可以快速準確得到空間群的方式。
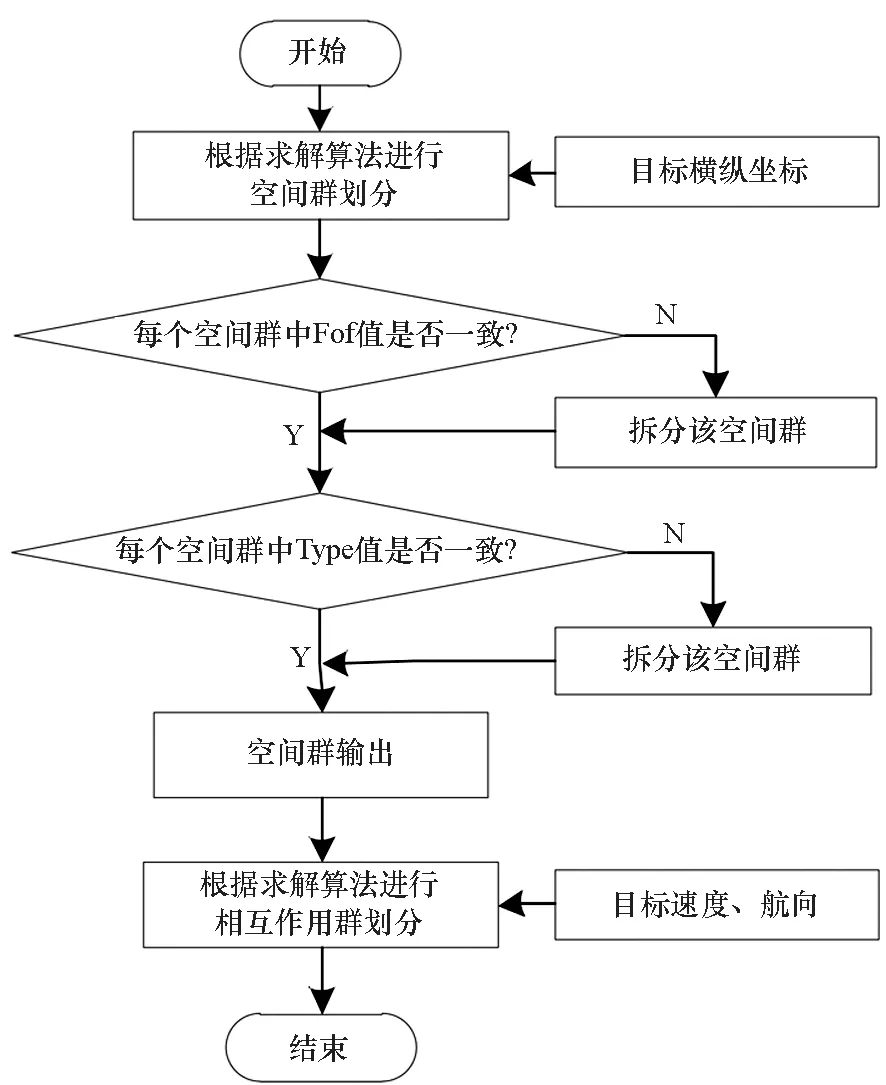
圖3 目標分群模型框架Fig.3 Target grouping model framework
2 改進的CBSCAN算法
CBSCAN是一種基于密度聚類(Density-Based Spatial Clustering of Applications with Noise, DBSCAN)算法[23]進行劃分改進的聚類算法。進一步改進CBSCAN的簇類擴展方法,以提高CBSCAN算法的聚類實時性。
2.1 DBSCAN算法
DBSCAN算法是一種應用廣泛的聚類算法。該算法主要通過鄰域范圍半徑ε和最小鄰域點數目閾值MinPts將數據點劃分為核心點、邊界點和噪聲點,繼而通過數據點之間的密度關系進行簇的劃分。DBSCAN算法的基本概念及其流程如下所述。
2.1.1 點的劃分
DBSCAN算法根據數據點密度及其位置關系,將數據點分為核心點、邊界點和噪聲點。劃分方法如圖4所示。
鄰域Nε(p):以數據點p為圓心,以鄰域范圍ε為半徑的圓形范圍內的數據點。表示為Nε(p)={q∈D|dist(p,q)≤ε},其中D為數據點集合,dist(p,q)為p,q兩點間的歐式距離。|Nε(p)|為p點ε鄰域內的鄰居點個數,以此表示數據點p的密度。
核心點:如果點p的鄰居點個數滿足|Nε(p)|≥MinPts,則點p為核心點。
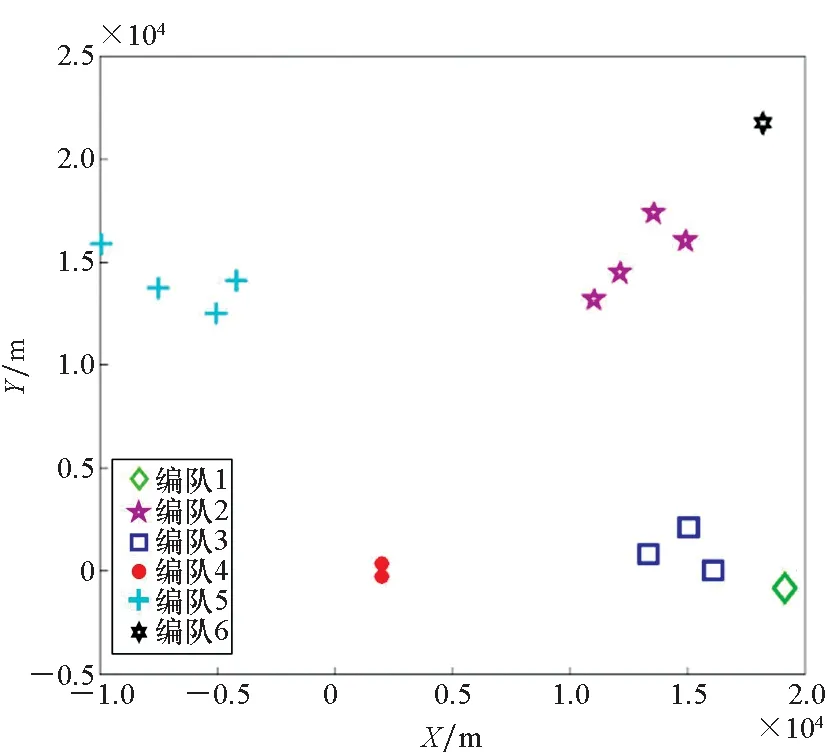
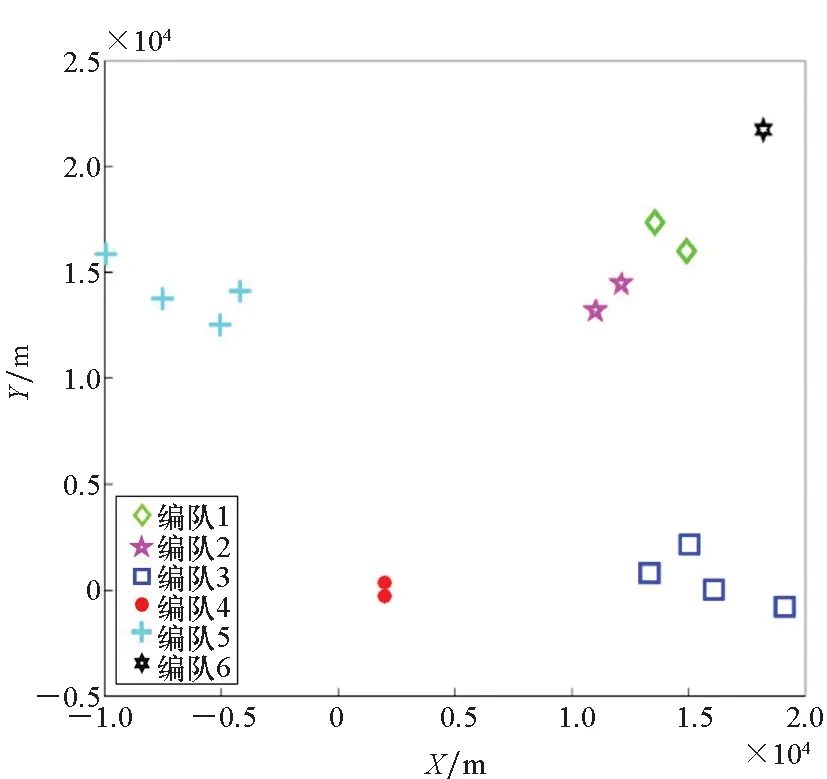
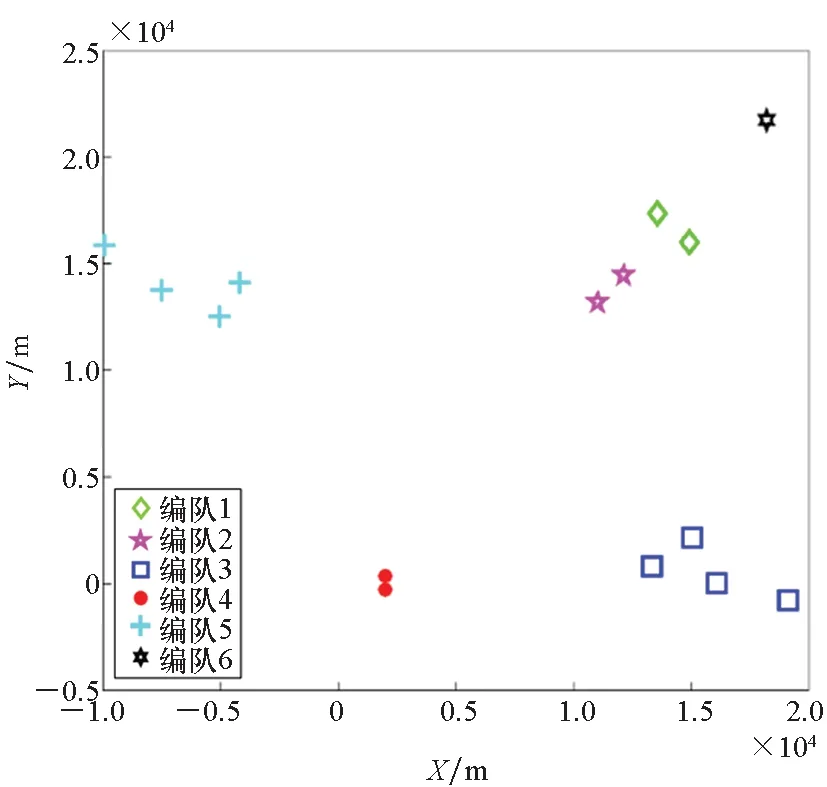
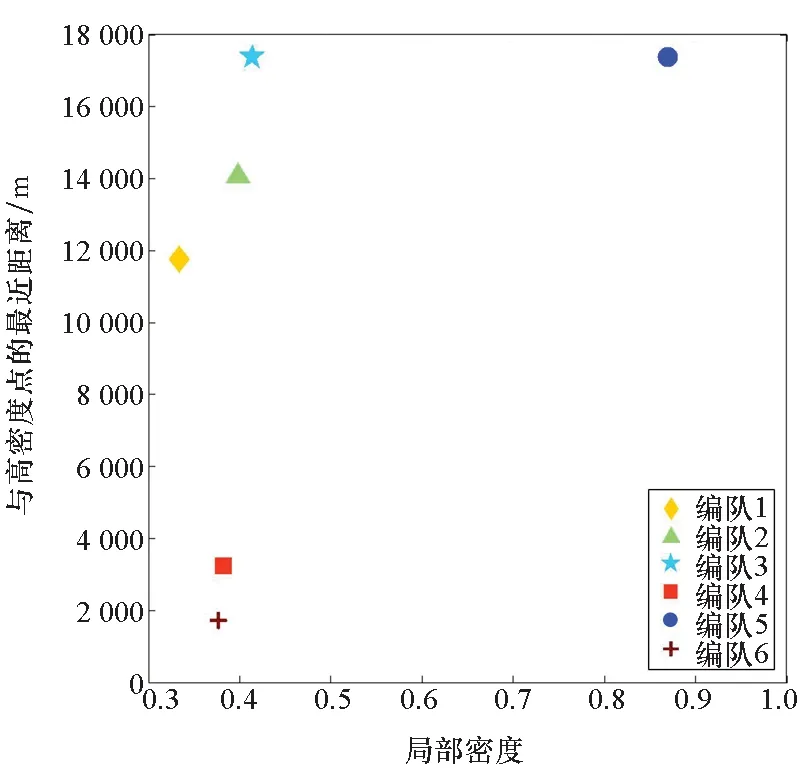
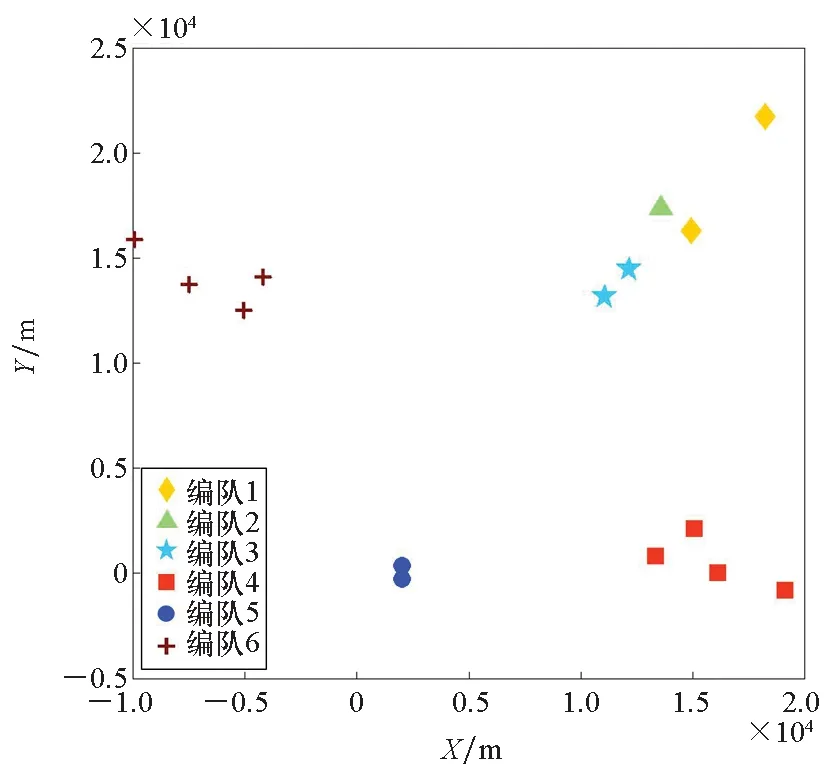
邊界點:如果點p的鄰居點個數滿足|Nε(p)| 噪聲點:如果點p既不是核心點,又不是邊界點,則該點為噪聲點。即鄰居點個數滿足|Nε(p)| 圖4 劃分流程Fig.4 Division process 2.1.2 密度關系 DBSCAN算法將同一簇中任意兩點間的密度關系分為直接密度可達、密度可達、和密度相連三種情況,進而由密度可達關系導出最大密度相連的樣本集合,以此為最終簇。 直接密度可達:如果位置點p滿足p∈Nε(q),且q為核心點,則點p直接密度可達點q,即點p直接密度可達其ε鄰域內的任一核心點。 密度可達:給定位置點p1,p2,…,pn,如果pi直接密度可達pi+1(i=1,2,…,n-1),則p1密度可達pn。 密度相連:如果點p和點q都密度可達點l,則點p與點q密度相連。 密度簇:所有密度相連數據點構成的數據集合。 2.1.3 算法流程 DBSCAN算法流程如圖5所示,DBSCAN算法從數據集合D中的任意一點p開始,檢索其ε鄰域中的數據點。如若|Nε(p)|≥MinPts,則將建立一個新的密度簇C,并對該簇進行擴展。由于DBSCAN算法需計算每個點的鄰域點數目,計算量較大,耗時較多。 圖5 DBSCAN 算法流程Fig.5 DBSCAN algorithm flow 圖6 CBSCAN算法網格劃分Fig.6 Meshing of CBSCAN algorithm 1)包含網格:給定某單元格G(b1,b2)和密度簇C,對于?p(p∈G(b1,b2)),若滿足p∈C,則G(b1,b2)是C的包含網格。 2)XG1型排他網格:若式(1)成立,則G(b1,b2)中數據點都是核心點,此時定義G(b1,b2)是某密度簇的XG1型排他網格。 (1) 由于G(b1,b2)周圍8格中任一點與G(b1,b2)中任一點(核心點)的距離都小于等于ε,根據直接密度可達關系,可以將包括G(b1,b2)在內的9格都劃為同一密度簇,此時G(b1,b2)周圍8格均為密度簇的包含網格。 3)XG2型排他網格:若式(1)不成立,則檢查G(b1,b2)周圍45格中數據點與G(b1,b2)中所有點間的距離關系。若?p(p∈G(b1,b2)),使得式(2)成立,則G(b1,b2)中存在核心點p,此時定義G(b1,b2)是簇的XG2型排他網格。由于G(b1,b2)周圍8格中的點與G(b1,b2)中核心點p的距離均小于等于ε,與XG1型排他網格相同,也可以將包括G(b1,b2)在內的9格劃為同一密度簇。 ∑qk≥MinPts (2) 此后,檢查排他網格的鄰居網格和含有邊界點的網格是否為排他網格,以此進行密度簇的擴展。CBSCAN算法流程如圖7所示。 圖7 CBSCAN算法流程Fig.7 CBSCAN algorithm flow 分析圖7所示流程可知,CBSCAN算法運用網格劃分的方式將數據點劃分到網格中,把數據點的查詢歸類轉化為網格的查詢歸類,較大地減少了DBSCAN算法的時間開銷。但該算法僅通過1個排他網格附帶周圍8個包含網格的方式進行簇類擴展,在高密度區的擴展效率依然相對較低。 1)XG3高密型排他網格:對于單元格G(b1,b2),若式(3)成立,則G(b1,b2)是XG3高密型排他網格。如圖8(b)所示,此時網格G(b1+i,b2+j),(i=-1,0,1;j=-1,0,1)均是XG1型排他網格,可向外擴展25個包含網格。 |G(b1,b2)|≥MinPts (3) (4) (5) (c) XG4中密型排他網格(c) XG4 exclusive grid (d) XG5次密型排他網格(d) XG5 exclusive grid圖8 排他網格示意圖Fig.8 Exclusive grid diagram 由上述定義分析可知,在CBSCAN算法中,當確定某網格G(b1,b2)為排他網格時,最多只能將9個包含網格擴展到密度簇中。通過提出高密、中密和次密型排他網格等概念,一次查詢最多可以擴展25個包含網格。 1)剔除異常值。空戰態勢數據中難免會存在部分異常值,常見的異常值處理方法主要包括刪除元組、數據補齊、缺失值處理和不處理等,采用刪除元組的方式處理異常值。孤立森林算法是一種無監督的異常檢測方法,它可以通過隨機分割數據集的方式,快速發現分布稀疏且離密度較高群體較遠的孤立點,能夠在低維數據集中取得良好的檢測效果。因此,采用孤立森林算法檢測并刪除飛行態勢數據中的異常值。 2)坐標系轉換。為了定量分析戰機間的相對態勢,將各型雷達獲取的目標數據統一到同一坐標系中。 3)歸一化處理。當態勢數據范圍不一致時,需要通過歸一化方法進行數據處理。 (6) 3.2.1 作戰空間網格劃分 分群模型在數據預處理的基礎之上,需要根據目標點di橫縱坐標的最大最小值和單元格邊長,由式(7)和式(8)確定網格的行數與列數。此后模型根據式(9)將所有坐標點分配到相應的單元格中,當坐標點處于網格邊線時,將該目標點歸屬到其右上方的網格中。 (7) (8) (9) 3.2.2 目標空間群擴展 基于改進CBSCAN算法進行空間群擴展的方式與圖7所示CBSCAN算法的執行流程大致相同,其區別在于改進CBSCAN算法有更多的排他網格擴展選擇。圖9所示為基于改進CBSCAN算法的目標分群模型。 圖9 基于改進CBSCAN的目標分群模型Fig.9 Target grouping model based on improved CBSCAN 同一空間群中的目標往往具有相同的敵我屬性和飛機類型。根據圖3目標分群模型框架,通過改進CBSCAN算法進行分群后,需根據敵我屬性和飛機類型的不同,對空間群進行拆分。 仿真硬件環境為:Intel(R) Core(TM) i7-7700HQ 2.8GHz處理器,16 GB內存,Win7 64位操作系統,軟件平臺為MATLAB 2014a。 多任務編隊協同空戰中的參戰飛機較多,涉及大量的飛行態勢數據。給出30組作戰場景想定,利用其中的飛行態勢數據檢驗改進CBSCAN算法處理空戰目標分群問題的適用性。每組想定中參戰飛機的數量不等,共有476個數據元組,每個元組都包括一架飛機的敵我屬性、飛機類型、坐標、飛行速度和航向等態勢數據。由于只針對敵方目標進行空間群分類實驗,所以設定所有數據元組中的Fof值為2。 圖10所示為其中一組典型空戰態勢,敵方共有15架飛機參與戰斗,他們欲通過偵察編隊、掩護編隊、轟炸編隊、伴隨干擾編隊和預警指揮編隊間的協同配合攻擊我方地面目標。 圖10 作戰想定Fig.10 Battle plan 表1數據為圖10作戰想定中的態勢數據。其中,類型 1為無人偵察機,類型2為殲擊轟炸機,類型3為電子干擾機,類型4為預警機,類型5為戰斗機。 表1 作戰想定飛行態勢數據 為驗證改進CBSCAN算法處理目標分群問題的有效性,分別利用K-means、最大期望(Expectation-Maximization, EM)算法、密度峰值、DBSCAN算法、CBSCAN算法和改進CBSCAN算法處理30組作戰想定中的飛行態勢數據。只分析算法處理空間群分類問題的有效性,故只對數據中的坐標位置進行聚類分析。 利用上述6種算法對圖10和表1所示飛行態勢數據進行10次目標分群實驗,將K-means和EM算法的聚類數目設置為6,實驗結果如圖11、圖12和圖13所示。 (a) K-means分群錯誤結果(a) Poor grouping results of K-means (b) K-means分群正確結果(b) Good grouping results of K-means (c) EM分群錯誤結果(c) Poor grouping results of EM (d) EM分群正確結果(d) Good grouping results of EM圖11 K-means、EM目標分群結果Fig.11 K-means, EM target grouping results (a) 決策圖(a) Decision diagram (b) 聚類中心選擇(b) Cluster center selection (c) 分群結果(c) Grouping results圖12 密度峰值算法分群結果Fig.12 Density peak algorithm target grouping results (a) 目標分群結果(a) Target grouping results (b) 平均運行時間(b) Average running time圖13 DBSCAN及其改進算法分群結果Fig.13 DBSCAN and its improved algorithm target grouping results 圖11為K-means算法和EM算法對作戰想定中15個空戰目標進行多次聚類后產生的部分不同結果。通過仿真實驗可以看出,在流形分布數據中,選擇不同的初始聚類中心會使K-means和EM產生不同聚類結果,這就使上述兩種算法的穩定性較差,且正確率較低。圖12為密度峰值算法的分群結果。在10次聚類中,該算法均產生了相同的錯誤分群結果,說明其穩定性較好,但正確率不高。圖11和圖12說明傳統聚類方法難以對流形分布的戰機編隊進行正確分群。圖13為DBSCAN、CBSCAN及改進CBSCAN算法的仿真結果。圖13(a)表明,DBSCAN及其改進算法對圖10所示作戰想定均得到了穩定且正確的分群效果,圖13(b)說明改進CBSCAN算法可以在保證正確率的同時,提高算法的執行效率。 為進一步說明改進算法的準確度和實時性,對30組作戰想定進行10次分群實驗,得到表2所示的仿真結果。 由表2結果可知:K-means算法執行效率較高,但其正確率較低且穩定性較差;EM算法執行效率低、正確率差且穩定性不好;此外,利用這兩種算法進行目標分群時,均需手動輸入類別數目,但目標分群屬于類數未知問題,故K-means和EM算法不適合處理空戰目標分群問題。密度峰值算法的時間復雜度較高,且由于該算法利用歐式距離作為相似性度量,無法準確對流形分布的空戰目標進行正確分類,導致其準確度與DBSCAN及其改進算法相比較差。DBSCAN、CBSCAN和改進CBSCAN三種算法的準確度較高,但改進CBSCAN算法的分群實時性在CBSCAN算法基礎上提高了約30%,達到了算法改進的目的。綜上,改進CBSCAN算法與其他算法相比,穩定性較好、準確度和實時性較高,能夠較好地處理編隊協同空戰中的目標分群問題。 表2 分群算法結果對比 1)K-means、EM和密度峰值算法難以對流形分布目標進行準確穩定的分群操作。 2) DBSCAN、CBSCAN和改進CBSCAN算法都可以對流形分布目標進行準確分群。 3) 通過改進CBSCAN算法的簇類擴展方式,可以在保證原始算法準確度的同時,將分群實時性提高約30%。 4)改進后的CBSCAN算法能夠在多編隊協同空戰背景下,對空戰目標進行準確且更加快速的分群編組。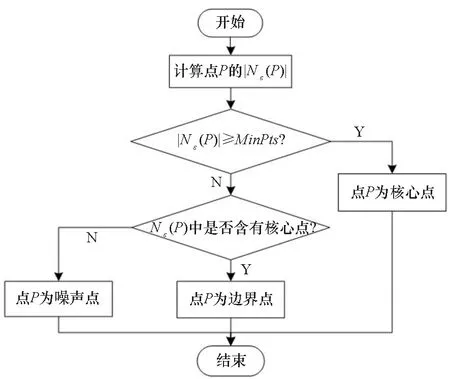
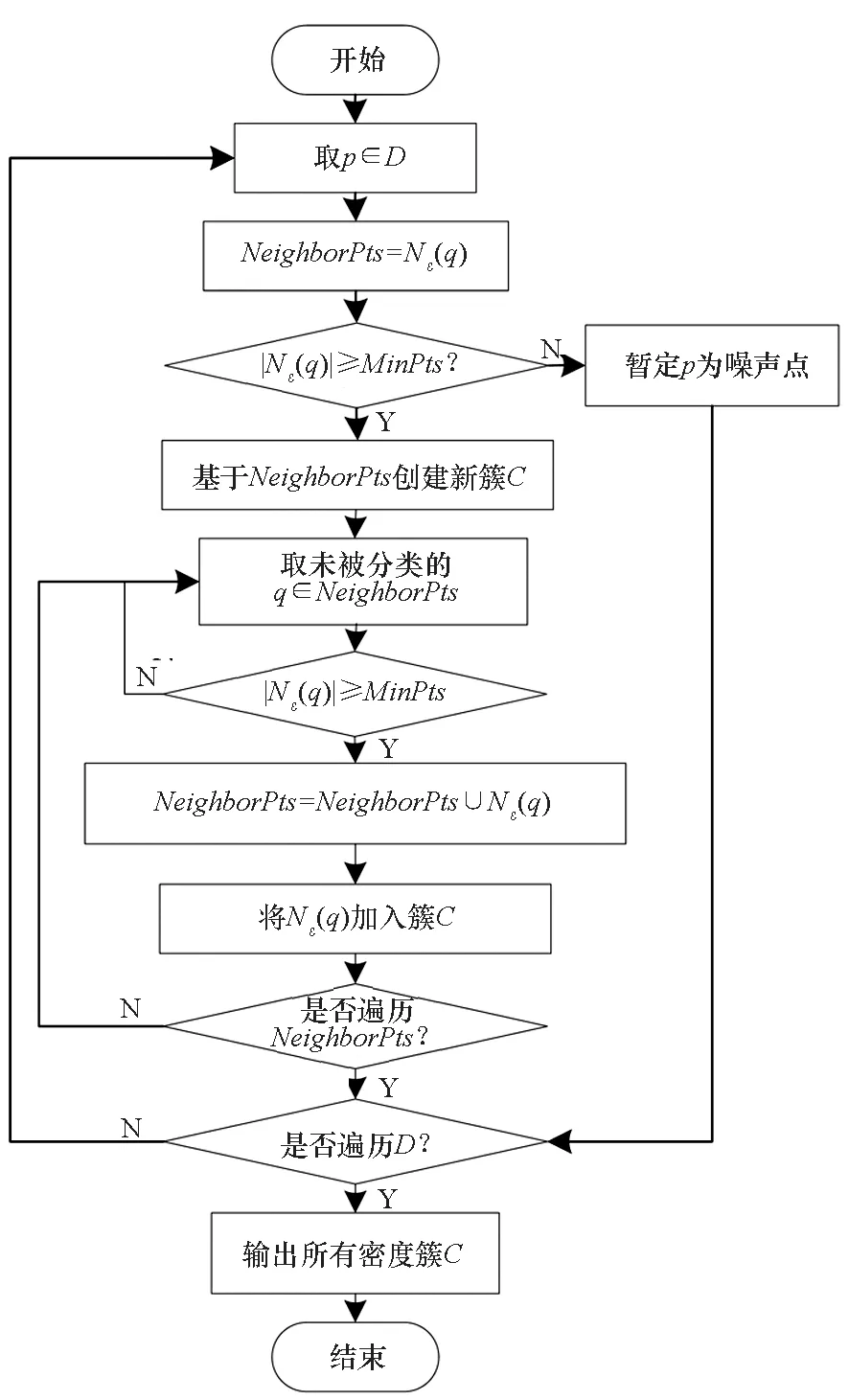
2.2 CBSCAN算法
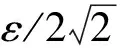
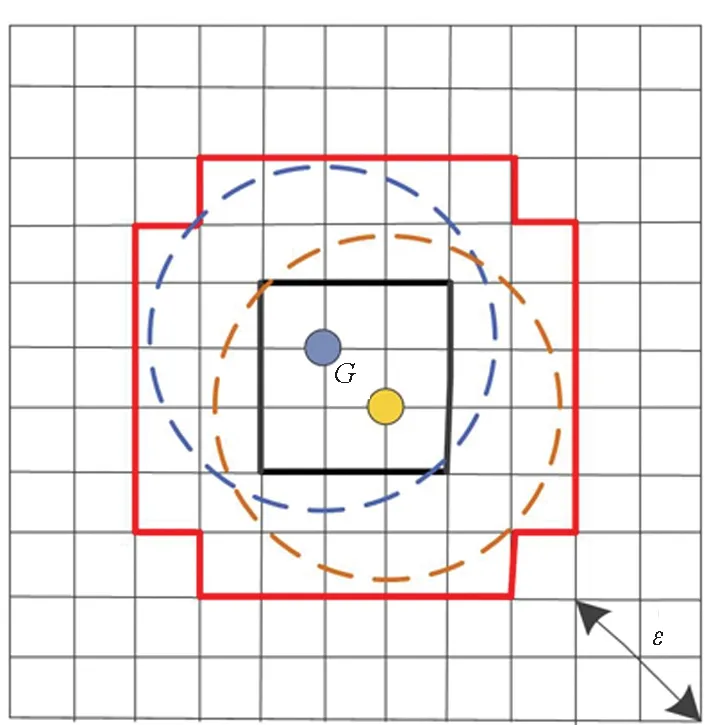

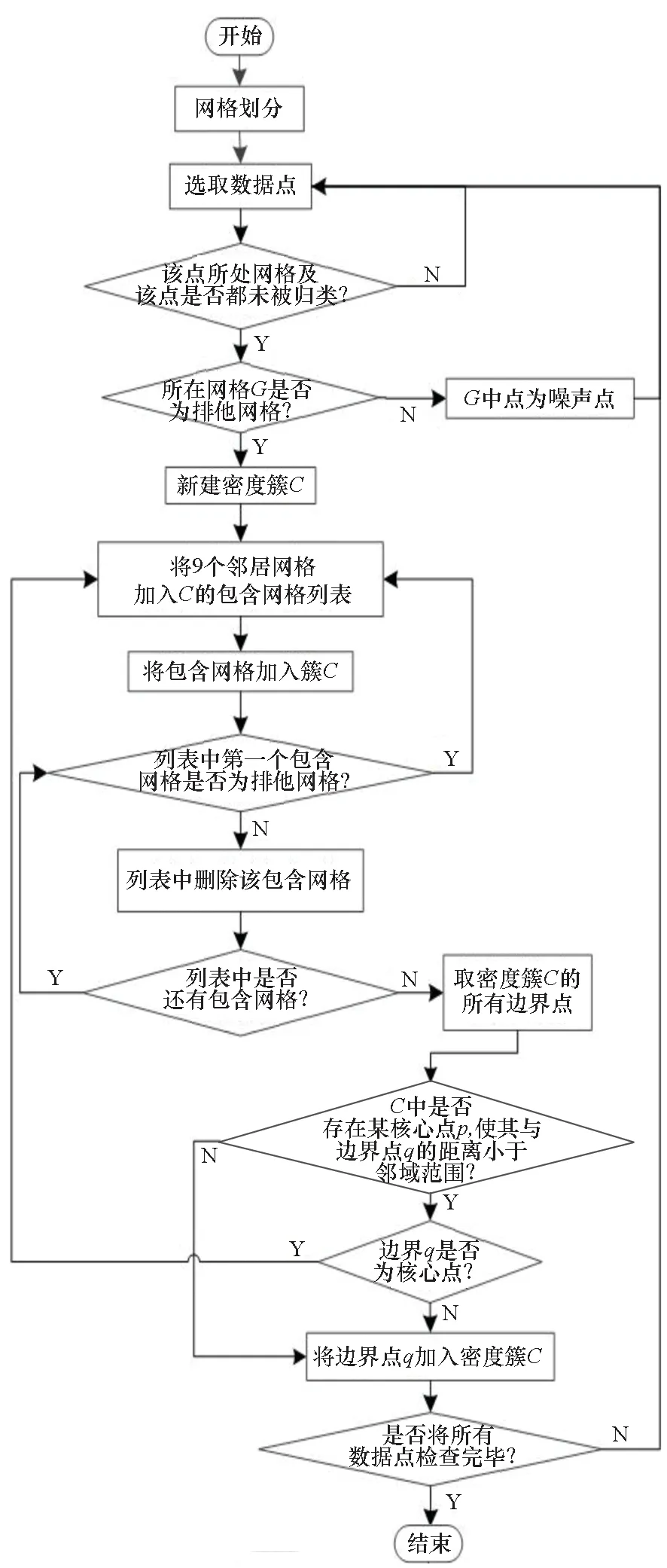
2.3 改進的CBSCAN算法
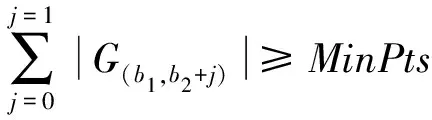
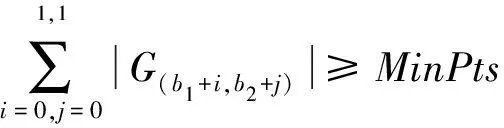
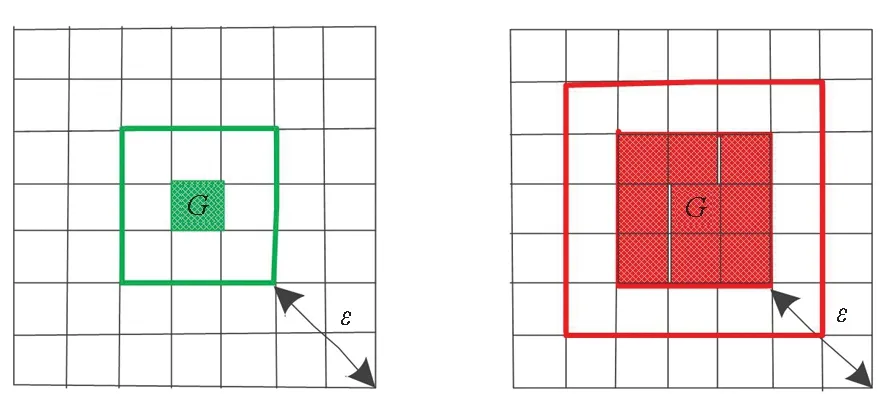
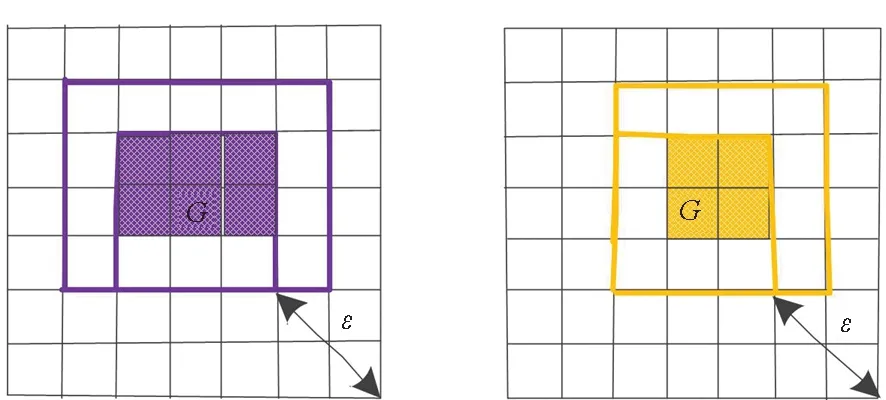
3 基于改進CBSCAN的目標分群模型
3.1 飛行態勢數據處理
3.2 模型的算法處理
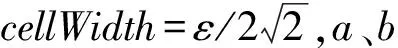
3.3 空間群拆分
4 仿真實驗
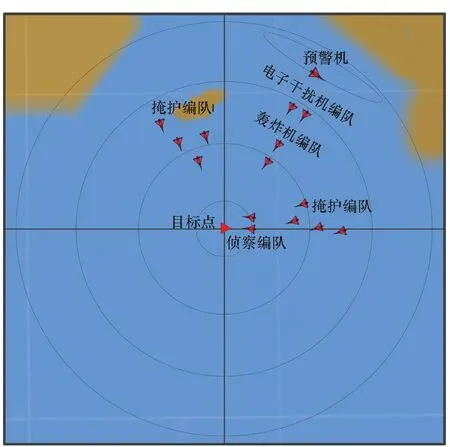
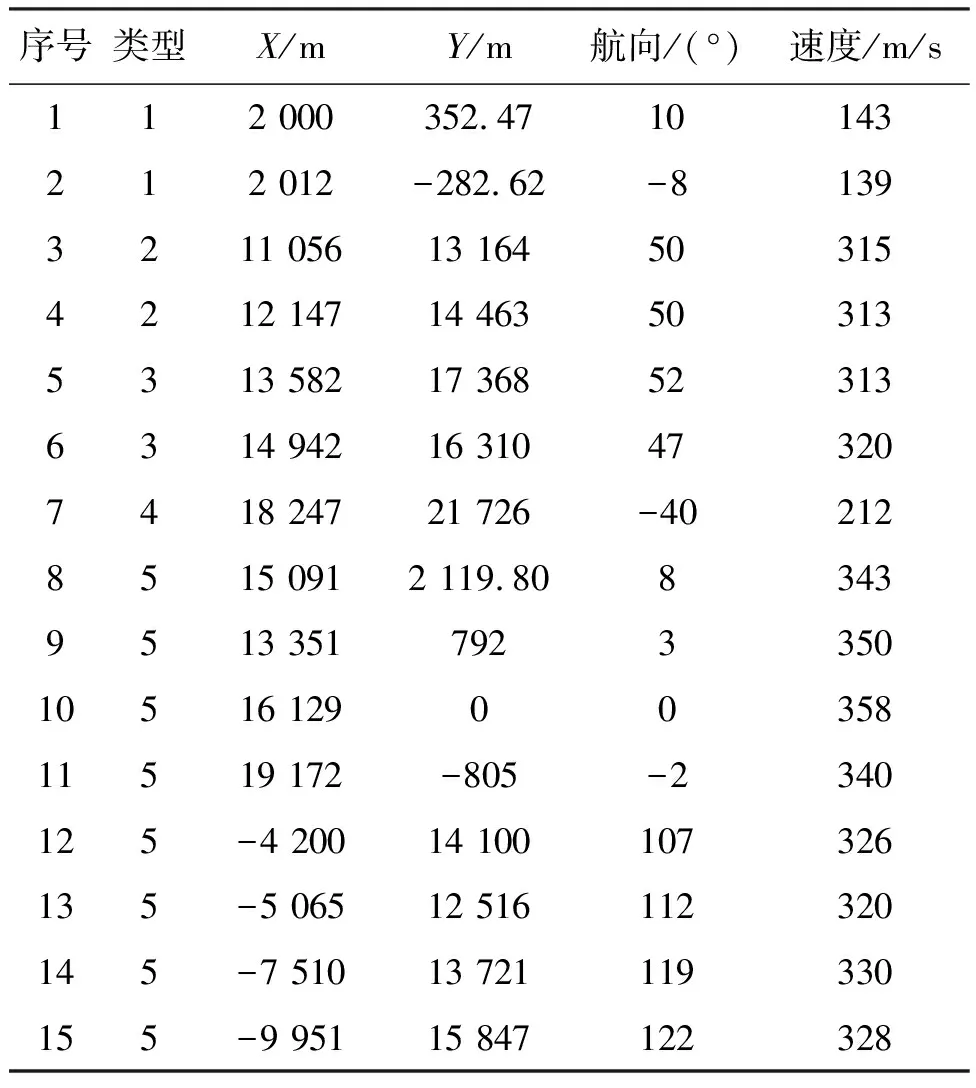
4.1 作戰想定分析
4.2 仿真結果
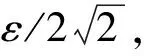
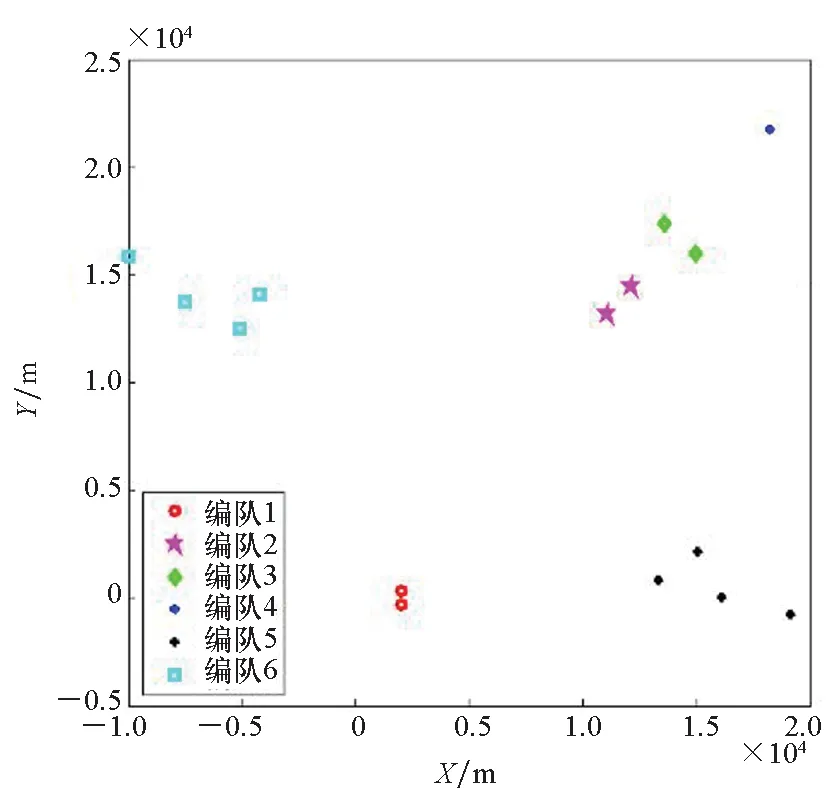

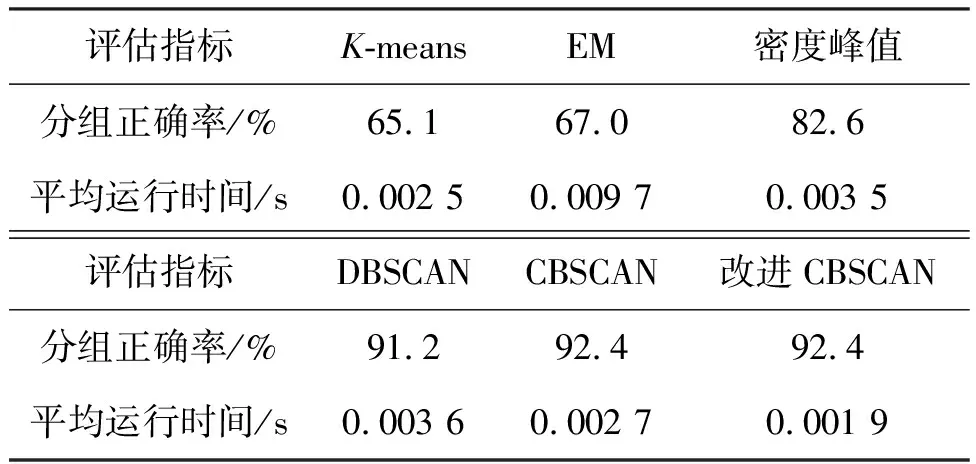
5 結論

