“多邊形的面積”單元整合教學探究

【摘要】本文針對“多邊形的面積”單元整合教學存在的問題，論述“多邊形的面積”單元整合教學的實踐策略：構建思維導圖，讓學生理解概念;以多練精講模式，幫助學生攻克求解難題;探究問題解決的方案，增強學生的自主學習意識。

【關鍵詞】小學數學 多邊形的面積 單元整合教學

【中圖分類號】G 【文獻標識碼】A

【文章編號】0450-9889（2021）21-0130-03

《多邊形的面積》選自人教版小學數學五年級上冊第六單元，這個單元涉及對圖形特點的感知、多邊形面積計算公式的理解與應用等知識點，綜合了三角形、平行四邊形、梯形等多種形狀及其組合的面積計算，具有鮮明的綜合性特征，為單元整合教學奠定內容基礎，既需要學生具備一定的幾何圖形認知及分析能力，還要靈活應用數字展開計算，綜合性較強、涉及面較廣，對教師的教和學生的學來說都具有一定的考驗性。

小學數學“多邊形的面積”這一章節的教學，是基于學生對現存概念認知不清、公式理解不到位、求解方法不善用等問題，這里的“整合”就是將不同單元、不同年級乃至不同教材相關聯的知識點綜合起來，由點到線、由線到面串聯成一個整體。三角形、平行四邊形等圖形的認知與計算，其實都是認識多邊形和進行多邊形面積計算的基礎，也是求解多邊形面積問題的必要條件。教師要整合單元內容，從構建概念導圖、優化練習模式、啟發學生自主探索等教學路徑出發，開展單元整合教學實踐，幫助學生突破“多邊形的面積”這一學習難題，從整體上提高學生的計算能力、拓寬學生的思維能力。

一、“多邊形的面積”單元內容分析

對小學生而言，“多邊形的面積”其實整體難度并不大，其中涉及的關鍵詞“多邊形”“面積”都是學生接觸過和學習過的概念。教師在本單元教學中，首先要帶領學生回顧三角形、平行四邊形、梯形等幾種多邊形的特點，并將這部分內容作為新授課的一部分，又是復習的一個環節。組合圖形由于融合了多類圖形，需要具體分析其特點，但大致離不開三角形、長方形、正方形、平行四邊形、梯形這幾類常見圖形。感知多邊形的特點是進行多邊形面積計算的基礎，教師幫助學生構建起對圖形的幾何回憶與印象，順勢引導后續內容的教學。其次，教師整理多邊形面積計算的各種公式，如S△=[12]ah（a是底邊，h是高，下同），S平行四邊形=ah，S梯形=[12]h（a+c）等，不僅要讓學生知道公式中字母所蘊含的意義，還要讓學生理解公式的形成過程。最后，基于圖形的認知和對公式的理解，要讓學生解決多邊形面積的求解問題，考驗學生的圖形感知、計算檢驗、解決問題、邏輯推理等多重能力，因此教師需要精心組織習題，有針對性地提高學生的學習能力。多邊形面積求解問題充分體現了數學與生活的關聯，有助于加深學生對多邊形面積計算方法和技巧的認識，并能夠將其轉化為解決問題的具體能力，通過探究性學習達成對實際問題的判斷、理解和解答。同時，教師也要把學科教學知識與課堂活動環節緊密結合，以自主探究或合作學習等方式，將求解問題正向遷移到學生的生活中去，讓學生在實際生活中體味數學的有效應用。

二、“多邊形的面積”單元整合教學存在的問題

（一）幾何概念認知不清

筆者在對“多邊形的面積”這一章節的實踐教學中發現，學生容易犯的一個突出毛病就是對幾何概念認知不夠準確，原因在于他們對圖形特點的認知不夠清晰。圖形構成有其固有的相似性，而利用多邊形可以幫助學生有效區分這些圖形類型。比如梯形和平行四邊形，梯形是一組對邊平行，一組對邊不平行，而平行四邊形是兩組對邊都平行，二者概念看似容易理解，但在形成具體的幾何圖形時，很多學生容易犯迷糊。

（二）計算公式理解不透

掌握公式是多邊形計算的中間步驟，學生需要建立幾何圖形直觀地感受與數理模型之間的聯系，觀察能力和計算能力缺一不可。比如三角形、平行四邊形和梯形面積計算公式中的“[12]”，時常會被學生忘記，導致計算錯誤。由于對計算公式理解不夠深入，學生時常“丟三落四”“改造公式”，一步錯，步步錯。在題目問題比較復雜的情況下，學生需要推導計算各個要素，有時即使陰差陽錯算出正確答案，也可能沒有完全理解和掌握該公式。

（三）求解方法運用不當

求解是多邊形面積計算的最后一個步驟，其所呈現的不僅是計算結果，還有計算公式與實際問題之間的聯結，充分考察了學生的實際應用能力。有的學生在直觀幾何圖形的面積計算中十分順利，但套用了“生活的外殼”，比如將三角形化為“紙飛機”、平行四邊形化為“水庫”、梯形化為“花壇”等，一時間找不準所需的計算要素和求解方式，以致容易出錯。還有的學生缺乏解題的創新性，因循守舊，計算結果雖然正確，步驟卻不夠簡便。而這種求解方法運用不當的情況，應回歸對計算公式的理解和對生活化體驗的問題上。

三、“多邊形的面積”單元整合教學實踐策略

（一）構建思維導圖，理解概念系統

《多邊形的面積》這一章節涉及復雜多樣的圖形，各種圖形既可以獨立成型，又可以相互組合、轉化，個性化和連接性的突出特點有助于學生構建思維導圖。教師既要密切各個圖形及其面積計算之間的聯系，又要突出每種圖形的個性特點。由于多邊形是由線和角構成，教師可以通過建立不同多邊形之間的聯系，構建思維導圖，幫助學生理解多邊形的概念。

多邊形之間的關系構建可以從圖形的組合與分割這一方向入手，如平行四邊形以對角線相切可以得到兩個完全相同的三角形，等腰梯形由上底兩端向下底做高線，則可以將之分割為兩個完全相同的直角三角形和一個長方形（或正方形），任何一個梯形都可以分割為一個平行四邊形和三角形等。通過了解這幾類多邊形之間的聯系，學生更加深入地感知多邊形的特點。

教師還可以帶領學生畫出多邊形特點對比的思維導圖或表格（如圖1），通過分析對比不同多邊形的特點，有關多邊形面積的概念也更為生動形象。構建思維導圖正是一個化零為整、相互融合的過程，圖形之間互有聯系，其面積計算公式之間也有關聯。例如，圖1所列的思維導圖，是將本單元中最重要的三角形、平行四邊形和梯形的面積公式及其推導方法明確列出，幫助學生整合單元知識，將面積公式內化于心，系統化地掌握單元所學。

（二）多練精講模式，攻克求解難題

多邊形面積涉及的概念雖然復雜，但本章節的最終目的是培養學生的公式應用和求解能力，練習環節是必不可少的。為了鞏固學生對多邊形面積計算公式的理解，還需要增設練習環節，根據學生的易錯點設置不同的練習側重點。在多練精講模式下，多練即為鍛煉學生對面積公式的理解應用能力，精講則是要從眾多習題中找出易錯、經典題型進行集中、細致地講解。這正是把《多邊形的面積》單元習題匯總在一處進行高效整合，將其中的優題提煉出來，幫助學生攻克求解難題。

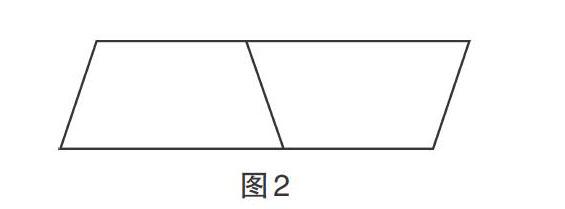
例如：一個梯形的上底是24厘米，下底是26厘米，高是18厘米，把兩個這樣的梯形拼成一個平行四邊形，求平行四邊形的面積？（如圖2）

此題給出計算梯形面積需要的上底、下底和高等信息，而且已經把平行四邊形拼成，無須學生思考拼法，因此重點應放在指導學生形成計算思路上。有的學生直接求得梯形面積再乘以2，有的學生則求出上底和下底之和再乘以高，算出平行四邊形的面積，最終得到的算式都是S=（24+26）×18。可見，對同一道題采用的計算思路因人而異，出現的問題或錯誤也各有不同。教師讓學生練習多邊形面積計算的習題，再對其中的易錯題目進行精細講解，有助于學生突破重難點和易錯點，促進學生對面積計算公式的深入理解和靈活運用，提升多邊形面積計算問題的解題效率。練習精講的模式，練習能夠有針對性地解決學生在“多邊形面積”學習遇到的題意理解、公式套用、計算等問題，可根據學生的易錯點各個擊破，克服求解過程的諸多難題，對學生整體的知識吸收與方法應用大有裨益。

（三）探究問題解決方案，增強學生自主意識

多邊形面積計算通常出現在問題解決的情境中，是以高度綜合的形式呈現在學生面前，教師應當采取科學合理的解決問題策略才能收到較好的教學效果。動手實踐、自主探究是突破障礙的最佳途徑，學生只有親身經歷實驗的過程，才能實現這一單元學習目的。

例如，求解平行四邊形的面積時，教師可以引導學生通過割補法將平行四邊形轉化為已學過的長方形，推導出面積計算公式。結合具體圖形實例，讓學生找出平行四邊形面積的求解與長方形之間的關系，并提供表格進行填寫。學生動手將平行四邊形和長方形互相轉化，如圖3中的平行四邊形都可以變換成為長方形，可知該平行四邊形的面積與長方形相同，面積計算公式同樣將底和高相乘，通過轉化可知兩側的小三角形面積相等，由此轉化前后的面積一致，再讓學生通過觀察圖3填寫表1，有助于啟發學生在探究問題的過程聯系不同的圖形，并通過動手操作聯想圖形之間的關系。

這一教學實踐是為了深化學生解決問題的意識，使其在審題中找出可能需要求解的問題，破解多邊形面積計算的易錯點、重難點，在解題中由被動變為主動，有助于將學生引向有效的“做數學”活動，不僅有效滲透數學轉化思想，而且更好地培養學生的多向思維和發散性思維。

綜上所述，“多邊形的面積”綜合了計算、邏輯思維、推理等多方面數理能力的培養，而且囊括多種圖形的特點，將零散的知識化為整體，單元的系統性和綜合性對小學生數學學習而言有一定的難度，但同時為教師進行知識整合、開展單元整合教學提供了思路。對此，教師應當采取多樣化的教學策略，為“多邊形的面積”這部分內容的教學提供相應的教學指導，結合學生在解決多邊形面積時存在的問題，幫助學生更好地整合所學、強化知識結構、提升數理邏輯思維能力。

【參考文獻】

[1]汪國祥.從內容疊加到融合——以“多邊形面積”教學為例談談對整合的實踐思考[J].中小學數學（小學版），2020（Z2）.

[2]李宇.為學生思維發展而教——以《多邊形的面積》單元教學為例[J].中國校外教育，2018（12）.

【作者簡介】李建軍（1977— ），男，漢族，甘肅張家川人，一級教師，現就職于甘肅省天水市張家川回族自治縣張家川鎮學區，研究方向為小學數學教學。

（責編 楊 春）