多徑條件下米波OFDM-MIMO雷達波束性能及特性分析

熊智敏，王黨衛，李星輝，馬曉巖

(空軍預警學院, 湖北 武漢 430019 )

頻率分集MIMO雷達[1]是MIMO雷達近年來發展的新方向，其所獨具的距離-角度分辨以及運動目標多普勒頻率分集效應為提升雷達多徑抑制和參數估計性能提供了新的契機。作為頻率分集MIMO雷達的應用，米波OFDM-MIMO雷達[2]近期研究已展示了良好的多徑抑制性能和參數估計性能，然而對其的研究尚處于早期探索階段，頻率分集MIMO雷達優勢應用和伴生的問題解決方法還遠未深入：一是現有頻率分集MIMO雷達信號模型研究往往未考慮米波工作時所受的多徑影響[3-4]，尚未考慮運動目標、多脈沖以及轉發式干擾等[5]，對米波OFDM-MIMO雷達回波中各分量時域、頻率、空域特性了解還不充分，制約了該體制雷達系統性能分析與對后續處理方法的研究。二是已有直接相關研究主要從檢測性能[6]和覆蓋盲區的角度[7]刻畫了米波OFDM-MIMO雷達多徑抑制的效果，缺乏抑制效果與陣列參數、頻偏、高度等解析表示，以及回波特性的系統研究。本節重點針對米波OFDM-MIMO雷達回波模型以及回波中不同成分特性進行研究。

1 米波OFDM-MIMO雷達信號回波模型

依據電磁散射理論，當目標有效尺寸與雷達波長大體相當時，目標散射將發生強烈的諧振現象，雷達后向散射(Radar Cross Section, RCS)值將顯著增加。文獻[3]指出，米波段電磁波長與現代用于實戰的空中目標有效尺寸相當，能大幅提高采用外形和材料隱身目標的雷達截面積。此外，相比更高頻段微波雷達，米波段雷達波長較長，地球表面反射系數更大，接近于1，多徑回波通常與直達波處于同一波束，會與目標回波相干疊加。

為了建模分析米波OFDM-MIMO雷達回波分量的特性，首先設定該雷達觀測幾何模型，如圖1所示，其采用M個陣元的等距線陣，陣元間距為d，距離地球表面高度為ha，以其第1個陣元中心建立坐標系，目標徑向距離記為RT，與陣列法向夾角記為θT。同時，設定OFDM-MIMO雷達工作于脈沖體制，陣列各陣元同時發射和同時接收，其第m個陣元發射信號頻率為

fm=f0+(m-1)Bm=1,2,…,M

(1)

其中，f0和B為初始載頻與相鄰兩個陣元發射信號載頻的頻率間隔。

進一步，設第m個陣元發射信號帶寬為B，脈沖寬度為Ts，調頻率μ=B/Ts，發射信號為

sm(t)=u(t)exp(j2πfmt)

(2)

其中，復包絡u(t)可表示為

u(t)=rect(t/Ts)exp(jπμt2) -Ts/2≤t≤Ts/2

(3)

此外，本節設定觀測場景中目標以及多徑反射點均位于陣列的遠場，且主要討論陣列與法向構成的二維平面內關系，其可擴展至二維陣列所形成的三維觀測場景。

1.1 米波OFDM-MIMO雷達目標多脈沖回波模型

設定目標RCS為σ，徑向速度為Vr(可取正值或負值)，則OFDM-MIMO雷達第n個陣元接收的第k個脈沖回波信號可表示為

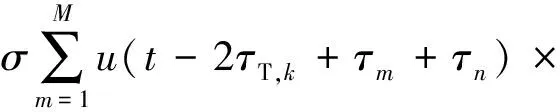
exp[j2πfm(t-2τT,k+τm+τn)]

(4)

其中，τT,k=[RT-(k-1)VrTr]/c為第k個脈沖目標徑向距離時延，τn=(n-1)dsinθT/c為接收時陣元間距時延，τm=(m-1)dsinθT/c為發射時陣元間距時延，Tr為脈沖重復周期。

更進一步，設定第n個陣元接收機結構如圖2所示，包含M個通道，第m個通道混頻器所使用的頻率為fm，經過下變頻和脈沖壓縮處理后，第n個陣元第m個接收通道基帶信號表示為

yT,knm(t)=αsinc[B(t-2τT,k+τn+τm)]×

exp[-j2πfm(2τT,k-τn-τm)]

(5)

其中，sinc(t)為辛格函數，α為脈壓后目標回波幅度。顯然，對于每個脈沖快拍，OFDM-MIMO雷達可形成M×M觀測通道。

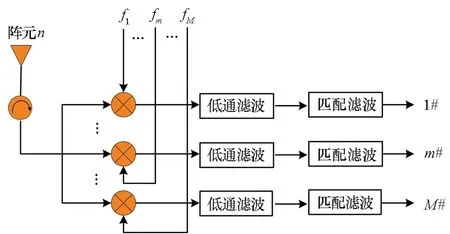
圖2 OFDM-MIMO雷達接收機結構Fig.2 OFDM-MIMO radar receiver structure

窄帶雷達陣元間位置差異對距離主瓣的影響可忽略，且一個相干處理間隔中K個脈沖回波主瓣距離不會走動，則若設λ0為f0對應波長，距離分辨率ρr=c/(2B)，回波信號yT,knm(t)可近似為

(6)

α′km=α′exp{[j2π(k-1)fdTr-R(m-1)/ρr+

fdTr(m-1)(k-1)/ρr]}

(7)

其中，α′=αexp(-j4πRT/λ0)為復系數，fd=2Vr/λ0為目標多普勒頻率。

若令回波相位ΦT,mn=2πfm(τn+τm)，則d?ρr時

(8)

于是，式(6)可改寫為

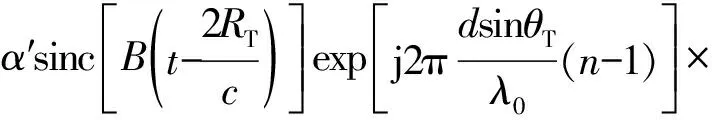
(9)

顯然，運動目標OFDM-MIMO雷達多脈沖回波相位包含3項，第1項對應接收導向信息，第2項對應發射導向信息，第3項對應脈沖維多普勒相位信息。特別是，當ρr值較小，即發射信號帶寬B較大時，第3項呈現出發射陣列空間維與脈沖維耦合特點，這顯然是文獻[8]建立模型沒有考慮的問題。此外，若設發射信號無頻偏，載頻均為f0，則OFDM-MIMO雷達退化為相控陣雷達[9-11]。

1.2 米波OFDM-MIMO雷達多徑回波模型

多徑效應是米波段固有的強電磁散射現象，米波雷達因較寬波束沿俯仰維“打地”，回波存在多種傳輸路徑，各路徑產生的多徑回波常與直達波強相關疊加，極易造成低仰角區域天線方向圖波瓣分裂，形成探測盲區和空域覆蓋不連續問題，已成為嚴重影響米波雷達低仰角區域測角性能的主要因素[12]。本文僅討論不考慮地球曲率的平面反射模型下OFDM-MIMO雷達多徑回波表達式[13]。結合圖1幾何模型，本文建立圖3所示單個地面反射點多徑幾何觀測模型，其中目標直達傳播距離為RT，高度為hT、距離陣列中心的水平距離為R0，直達波相對陣列法向的俯仰角為θT，多徑反射點相對陣列法向的俯仰角為φ，則根據幾何關系可得目標的多徑傳播距離RT、Rs分別為[14]

(10)

(11)

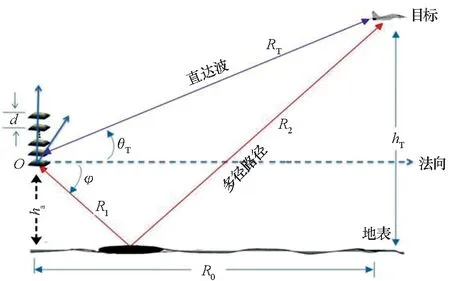
圖3 多徑幾何觀測模型Fig.3 Multipath geometric observation model

當低仰角觀測時，R0?hT和R0?ha，Rs近似為[15]

(12)

(13)

可解得多徑散射點位置為(Ru,-ha)，其中

(14)

因此，若設地面復反射系數為η，忽略空間傳播過程中電磁波的能量衰減，則可知第k個發射脈沖信號到達目標處的信號可表示為

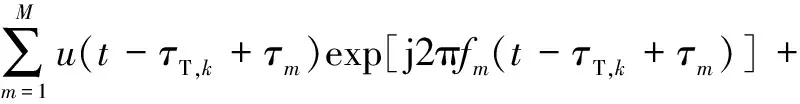
(15)

其中，τT,k和τm與式(4)定義相同，τs,k=Rs,k/c為多徑傳播距離對應時延，Rs,k可由RT,k關系導出。

若進一步設目標RCS記為σ，則第n個陣元接收的第k個脈沖多徑回波可表示為

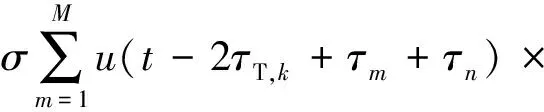
exp[j2πfm(t-2τT,k+τm+τn)]+

exp[j2πfm(t-τs,k-τT,k+τm+τn)]+

exp[j2πfm(t-2τs,k+τm+τn)]

(16)

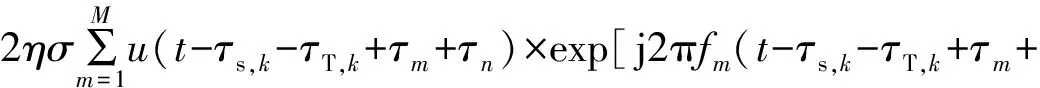
ys,knm(t)≈ε1sinc[B(t-τT,k-τs,k)]×

exp[-j2πfm(τT,k+τs,k-τm-τn)]+

ε2sinc[B(t-2τs,k)]×

exp[-j2πfm(2τs,k-τm-τn)]

(17)

其中，ε1、ε2均為多徑回波分量的系數。ys,knm(t)解析表達式為

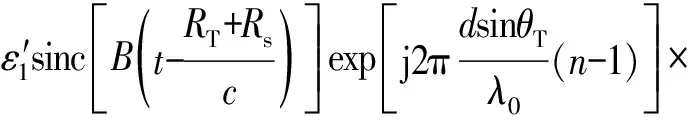
(18)

其中，若令地面復反射系數η=-1，σ′為脈沖壓縮輸出目標等效RCS，則

ε′1=-2σ′exp(-j2π(RT+Rs)/λ0)

(19)

ε′2=σ′exp(-j4πRs/λ0)

(20)

不難發現，多徑效應使得回波中產生了2項附加項，其與直達波目標回波相似，差異主要體現在距離維主瓣時延和陣列位置相關的空間維。同時，多徑回波的多普勒頻率與直達波回波相同，均由目標徑向運動速度決定。本節僅建立了單個地面反射點的多徑回波模型，對于實際波束照射區域內多個反射點多徑回波，可通過改變ha獲得。

2 米波OFDM-MIMO雷達回波特性分析

2.1 米波OFDM-MIMO雷達單次快拍回波特性

OFDM-MIMO雷達第k個脈沖快拍回波具有三維結構，如圖4所示，包含時延對應的距離維、M個發射陣元對應的空間維和各陣元M個接收通道對應的頻率維信息，其中ρr=c/(2B)為距離維分辨率。

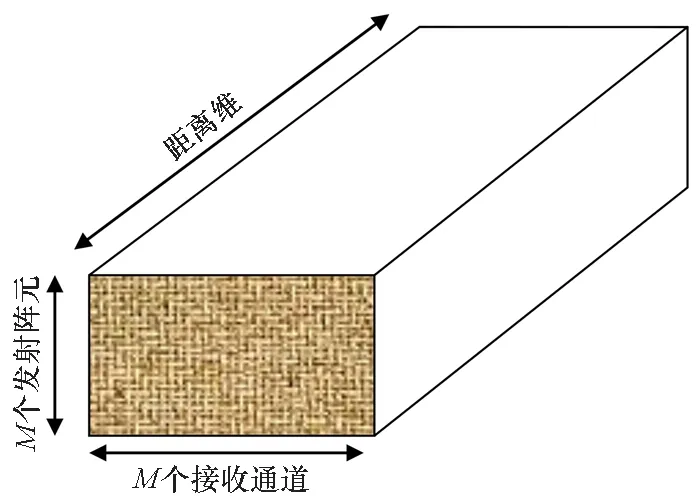
圖4 單次快拍回波結構Fig.4 Single snapshot echo structure

當目標、多徑距離超過距離分辨率對應時間寬度時，主瓣會出現在不同距離單元，而若時延差小于距離分辨率對應時間寬度時，則會在同一距離單元疊加。相位信息中包含了目標、多徑的距離信息，當距離信息給定后，相位信息是與時間t無關的量，差異僅為幅度的不同。

因此，第k個脈沖第l個距離采樣回波ykl=[yk,11,yk,12,…,yk,1N,yk,21,…,yk,NN]T∈MM×1為

ykl=ξT,kla(θT,RT)?b(θT)+

ξS2,kla(θT,Rs)?b(θT)

(21)

其中，ξT,kl、ξJ,kl和ξS1,kl分別為目標和多徑信號復幅度，a(θ,r)∈M×1和b(θ)∈M×1為發射和接收導向向量，分別可表示為

(22)

(23)

(24)

(25)

(26)

(27)

發射導向向量是距離和角度的二維函數，接收導向向量僅是角度的函數。OFDM-MIMO雷達陣列本身的收發雙程方向圖函數為[16]

G(θ,r)=GT(θ,r)GR(θ)

(28)

其中，GT(θ,r)和GR(θ)為發射和接收方向圖，則

(29)

(30)

且ψT(θ,r)=(M-1)π(dsinθ/λ0-r/ρr)，ψR(θ)=(M-1)πdsinθ/λ0。

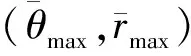
(31)

由sin(πx)的周期性可知

(32)

對應可導出發射方向圖半功率寬度為

(33)

米波OFDM-MIMO雷達陣列具有距離和角度兩維分辨能力，其發射方向圖具有距離角度耦合特性，尤其是在距離維具有周期性，頻率間隔等于信號帶寬，周期對應的距離為ρr，半功率寬度遠小于ρr；接收方向圖則僅是角度θ的函數。

相對地，相控陣陣列的方向圖可表示為

G(θ)=GT(θ)GR(θ)

(34)

其中，GT(θ)和GR(θ)為發射和接收方向圖。忽略共同包絡幅度和相位的影響，徑向距離RT、角度θT處米波OFDM-MIMO雷達陣列增益為

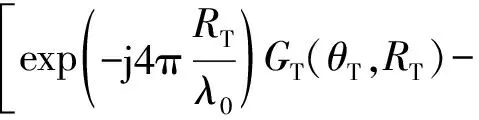
(35)

當存在多徑時該處相控陣雷達增益可表示為

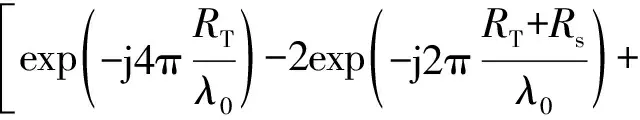
(36)

OFDM-MIMO雷達中，直達波與多徑傳播路徑存在距離差，一次多徑距離差ΔRs1可表示為

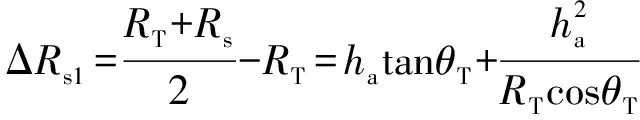
(37)

而二次多徑距離差ΔRs2為

(38)

顯然，若ha和RT取值使得Δr1/2<ΔRs1，則陣列法線方向一次多徑和二次多徑方向圖主瓣在距離維將與直達波方向圖主瓣分離。特別地，當一次多徑距離差ΔRs1滿足

(39)

此時，一次多徑方向圖處于直達波零增益位置，可完全消除一次多徑對直達波的抵消，二次多徑距離差ΔRs2為

(40)

即二次多徑與直達波主瓣位置近似重合，若相位同向，則會增強主瓣增益。

上面分析表明，給定距離分辨率ρr時，多徑距離差ΔRs1和ΔRs2隨ha正比變化，隨RT反比變化，即增大天線高度有可能減小多徑影響，且隨著RT增大，為減弱多徑影響需提高天線高度。此外，給定天線高度，減小ρr增加多徑距離差相對直達波的偏移，也可減小多徑的影響。此外，需要指出的是，本節僅從陣列法線方向單次回波的特性，實際上雷達為了覆蓋觀測空域，常需要改變波束的指向，即進行波束形成處理。而由于陣列方向圖的距離依賴特性，米波OFDM-MIMO雷達波束形成的權值將與傳統相控陣雷達不同。

2.2 米波OFDM-MIMO雷達多次快拍回波特性

前一小節，本文利用陣列方向圖研究了米波OFDM-MIMO雷達單次快拍回波特性，為了實現多脈沖的相參處理，本小節進一步研究其回波多脈沖特性。事實上，目標、多徑回波與脈沖維的關系具有統一的表達式，為此，本節僅研究表征脈沖維關系式的變化特性，而忽略復幅度的影響。由此可知，回波各分量脈沖維關系式可表示為

(41)

其中，(m-1)(k-1)fdTr/ρr為發射頻率分集波形后耦合項。第m個發射通道的等效多普勒頻率為

(42)

即各通道等效多普勒頻率不同，相鄰通道多普勒頻差為fd/ρr，(M-1)fd/ρr為最大多普勒頻差。當ρr較小時，發射頻率分集波形對多普勒頻率值產生放大效應。更進一步，對第m個發射通道沿脈沖維進行離散傅里葉變換，則幅度譜為

(43)

其中，fk為k對應的離散頻率，K為脈沖數。由前文結論可知，幅度譜|Ψ(fk,m)|主瓣中心位于fdm,主瓣半功率譜寬為Bk=0.88/KTr=0.88fr/K。

若相鄰通道多普勒頻差為fd/ρr>Bk，則

(44)

等效多普勒頻率將會在發射通道間出現走動，且隨K的增大越發明顯。這表明，米波OFDM-MIMO雷達遠程探測時，因fr較小，較高徑向速度目標產生的等效多普勒頻率與多普勒頻率差fdm-fd會超過Bk，使得在相干處理時間內各發射通道多普勒頻率出現超過Bk的走動問題。 同時，由離散傅里葉變換性質可知，其可表征的頻率范圍為fr/2，這就意味著fdm較大時，即(m-1)fd/ρr走動超過fr/2，產生頻譜折疊問題。

3 仿真分析

本節主要對米波OFDM-MIMO雷達陣列直達波、多徑條件下方向圖，單次和多次快拍回波進行仿真，設置該雷達載頻為150 MHz，發射信號樣式為LFM信號，頻偏和帶寬取值處于150 kHz～15 MHz范圍，脈沖重復頻率為0.03 s，脈沖寬度為150；陣列陣元數為10，陣元間距為1 m，陣列高度取值100～2 000 m。

3.1 仿真1：直達波方向圖仿真

設定B=1.5 MHz，距離為30～31 km，距離采樣間隔為2 m，角度為-90°～90°，采樣間隔約為1.78°，仿真產生直達波陣列方向圖。圖5給出了發射方向圖與其法線角度切片圖。由圖5仿真結果可以看出，OFDM-MIMO雷達發射方向圖呈現距離-角度耦合特性，在距離維以ρr=100 m為周期等間隔分布，幅度約為9.9，半功率點寬度約為8.79 m，其第1副瓣電平約為-13.2 dB，與理論分析吻合；圖6給出了接收方向圖與其法線角度切片圖。圖6接收方向圖僅與角度有關，幅度約為9.9，半功率點寬度約為0.056π，等于10.08°，其第1副瓣電平約為-12.87 dB，考慮角度采樣偏差，結果與理論分析吻合。圖7給出了收發雙程方向圖及其切片圖。此外，圖7收發雙程方向圖也呈現距離周期特性，周期為ρr=100 m，幅度約為98，距離維半功率點寬度約為9 m，其第1副瓣電平約為-12.98 dB，而角度維半功率點寬度約為7.2°，距離維主瓣寬度和副瓣電平不變，角度維主瓣寬度更窄、副瓣電平更低。

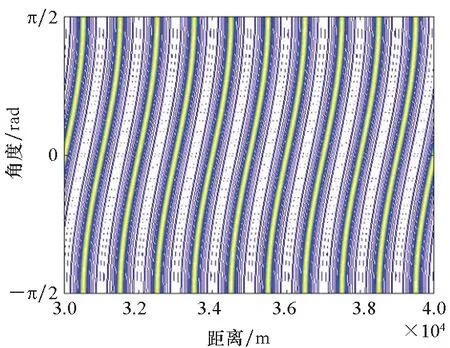
(a) 投影圖(a) Projection

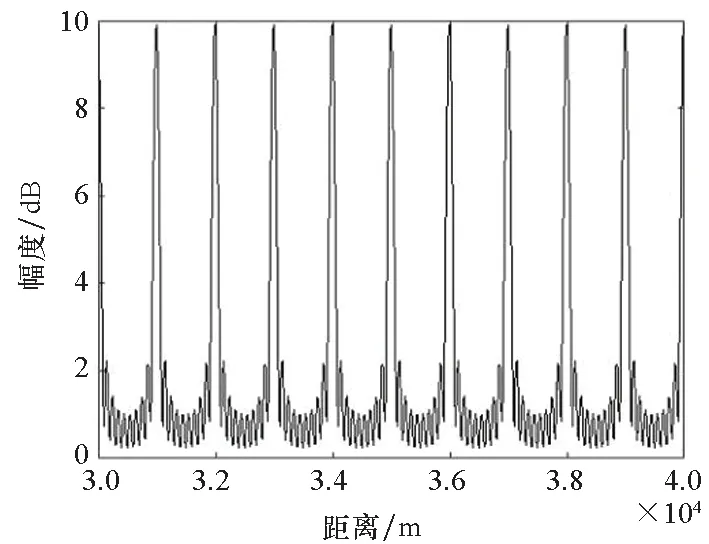
(b) 切片圖(b) Section diagram圖5 發射方向圖與其法線角度切片Fig.5 Slicing of emission direction diagram

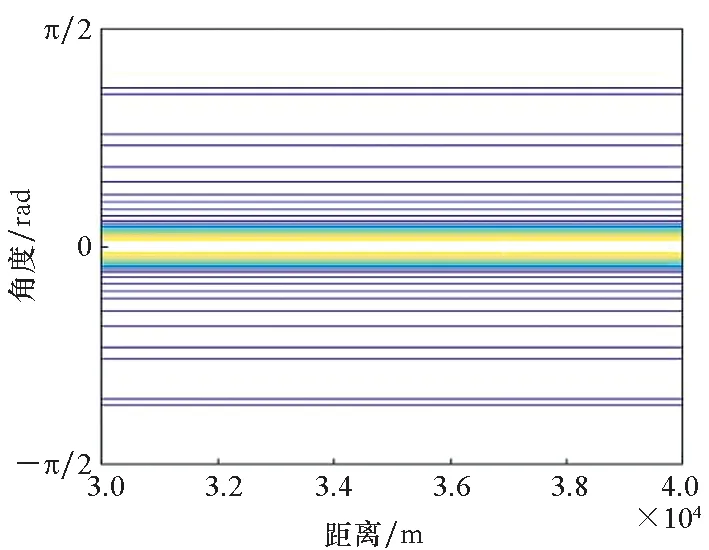
(a) 投影圖(a) Projection

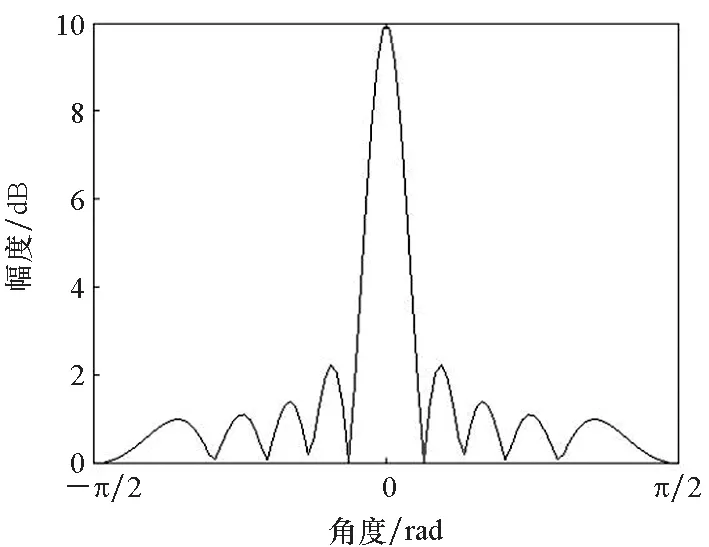
(b) 切片圖(b) Section diagram圖6 接收方向圖與其法線角度切片Fig.6 Receiving pattern and its normal angle section

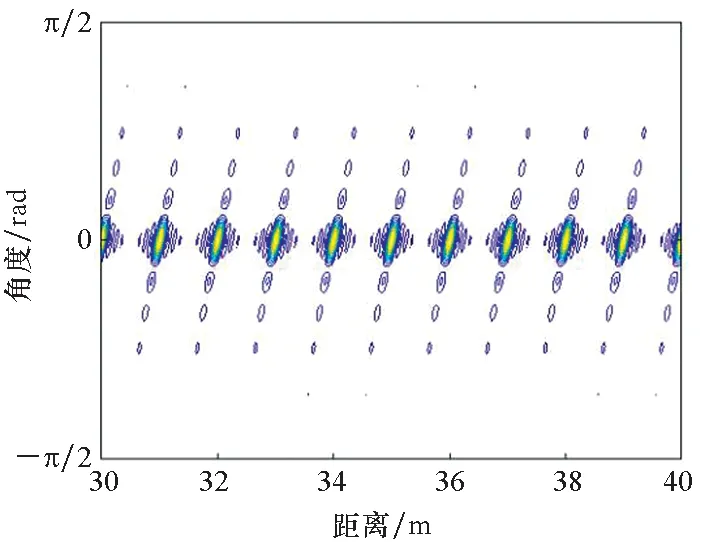
(a) 投影圖(a) Projection

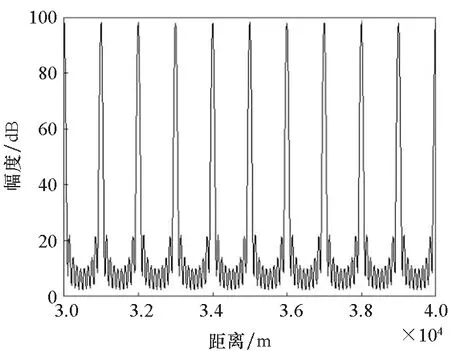
(b) 角度切片圖(b) Angle section diagram

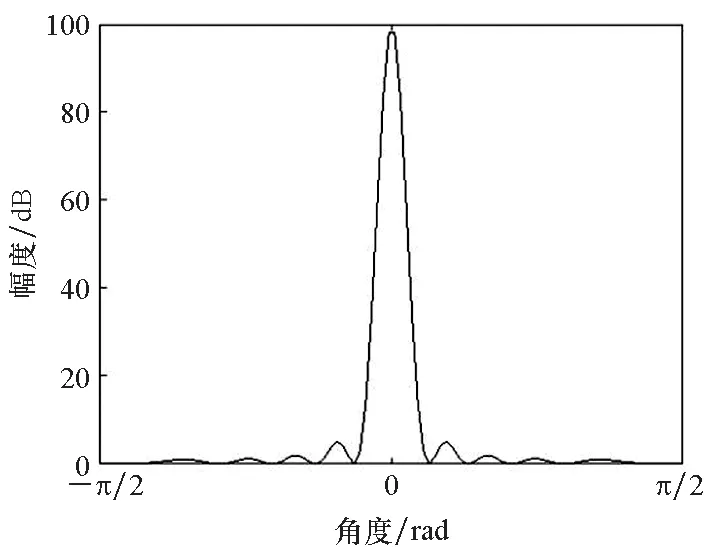
(c) 距離切片圖(c) Distance slice diagram圖7 收發雙程方向圖與其切片Fig.7 Transceiver dual deviation chart

3.2 仿真2：多徑條件下方向圖仿真

為了測試和驗證多徑對米波OFDM-MIMO雷達收發雙程方向圖的影響，主要仿真不同天線高度時米波OFDM-MIMO雷達雙程方向圖法線方向功率，并將同等條件下相控陣雷達方向圖功率作為對比。實驗中首先設定頻偏B=1.5 MHz，直達波主瓣指向(30.1 km，0°)，陣列高度ha取值由100 m增加至2 000 m，其他參數同上，圖8給出了收發雙程方向圖功率隨陣列高度變化曲線。隨著天線高度的增加，米波OFDM-MIMO雷達方向圖多徑條件下更為穩定，天線高度超過510 m后(利用Δr1/2<ΔRs1求得的ha≈514.66 m)，逐漸穩定于40 dB，很好地抑制多徑效果。隨天線高度的變化，多徑條件下相控陣雷達方向圖功率則劇烈起伏，存在較深的低增益區，這反映了方向圖存在明顯的波瓣分裂問題。

分別設定頻偏B=15 MHz，直達波主瓣對應指向(31 km，0°)和(30.01 km，0°)，其他參數同上，多徑收發雙程方向圖功率隨陣列高度變化曲線如圖9所示。增大頻偏能提高OFDM-MIMO雷達多徑抑制效果，在部分高度出現相干疊加效應，且要求的天線高度也隨之降低，如B=15 MHz時，功率穩定在40 dB所需天線高度約162.75 m，在550 m、770 m、945 m等高度方向圖功率約50 dB。

圖9 雙程方向圖幅度隨陣列高度變化曲線(B=15 MHz)Fig.9 Curve of variation of amplitude of dual-path pattern with array height(B=15 MHz)

3.3 仿真3：米波OFDM-MIMO雷達回波仿真

設置該雷達發射信號樣式為LFM信號，頻偏B=1.5 MHz，距離維采樣頻率取40 B，脈沖數為32，陣列高度ha=520 m，徑向速度為210 m/s的目標位置位于(30 km，0°)，其他參數同前。圖10給出了米波OFDM-MIMO雷達第1個脈沖回波壓縮結果與M2個通道回波相干累積結果，同時給出了相控陣雷達回波。受多徑影響，相控陣雷達相干累積回波距離維出現3個峰值，存在明顯的多徑回波，位于30.26 km和30.52 km處，而目標回波幅度為8.54×105，約為小于一次多徑回波的一半；而米波OFDM-MIMO雷達回波距離維僅包含目標回波峰值，位于30 km處，幅度約為9.16×105，較好地抑制了多徑。

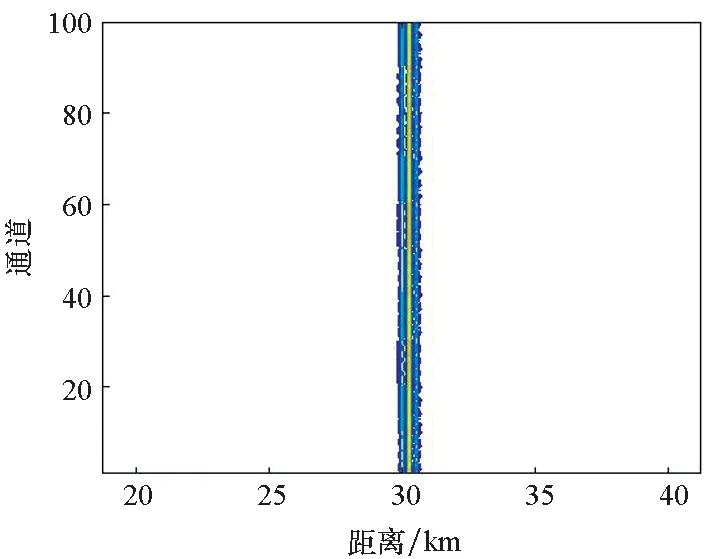
(a) OFDM-MIMO回波投影(a) Echo projection

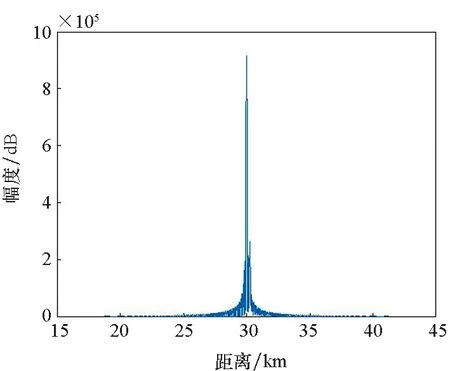
(b) OFDM-MIMO累積回波(b) Cumulative echo

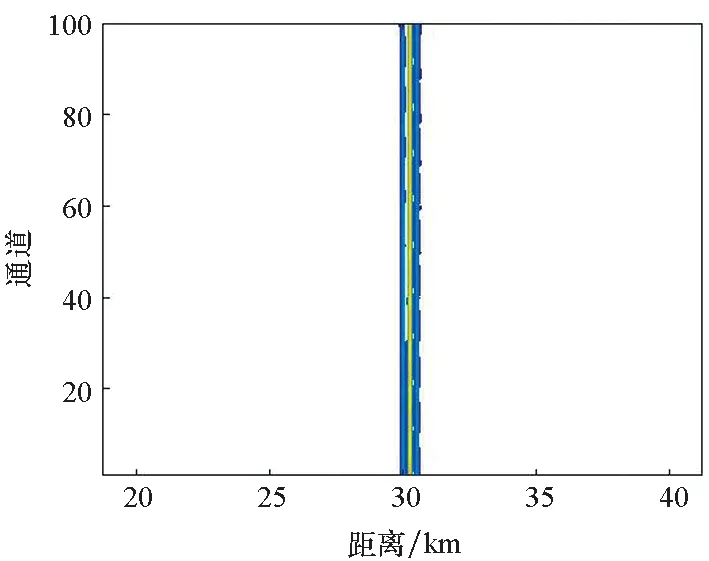
(c) 相控陣回波投影(c) Echo projection

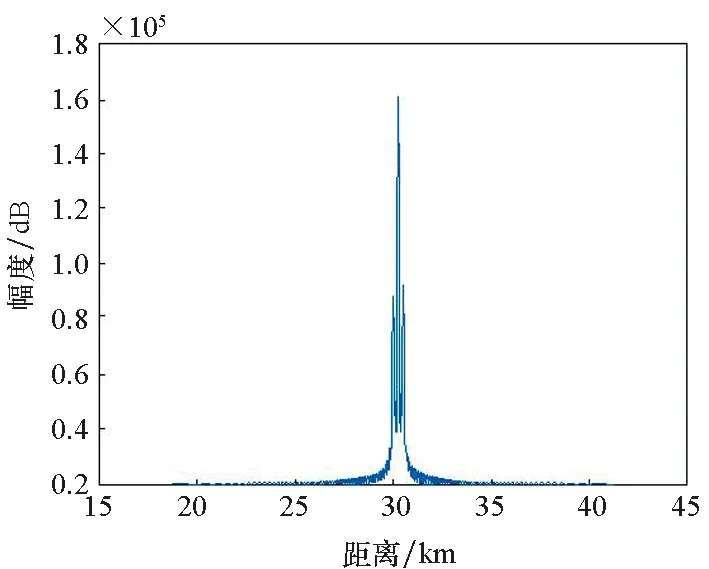
(d) 相控陣累積回波(d) Cumulative echo圖10 兩種雷達多徑回波仿真結果Fig.10 Multipath echo simulation results of two kinds of radar echoes

此外，進一步對圖10仿真的回波和第4陣元M個通道脈沖目標距離主瓣回波進行脈沖維離散傅里葉變換，且對相控陣雷達進行同樣處理。圖11給出了兩種雷達回波多脈沖處理結果。米波OFDM-MIMO雷達回波因發射通道與脈沖維耦合，回波多普勒頻率沿通道存在較大變化，出現明顯的多普勒單元走動現象，而相控陣雷達則無此現象，與前文分析吻合，進一步證實了前文所建立信號模型和特性分析的正確性。

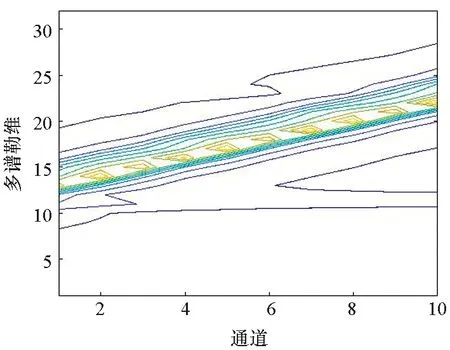
(a) OFDM-MIMO陣元4(a) OFDM-MIMO element 4

(b) 相控陣陣元4(b) Phased array radar element 4圖11 兩種雷達回波多脈沖處理結果Fig.11 Multi-pulse processing results of two kinds of radar echoes

4 結論

本文提出的米波頻率分集MIMO雷達能夠在接收端實現距離依賴波束，從而有效地抑制了多徑，改善了波束覆蓋性能。理論和仿真都表明，米波頻率分集MIMO雷達體制具有更優的低空波束覆蓋性能，所提的固定頻偏設計方法能夠實現有效連續覆蓋，這對低仰角下的目標檢測和跟蹤將大有裨益。理論和仿真實驗研究表明：

1)米波OFDM-MIMO雷達陣列雙程方向圖具有距離-角度二維分辨能力，因發射頻率分集，陣列雙程方向圖法線方向主瓣距離維以ρr為周期分布，半功率寬度(對應于陣列距離分辨力)約為0.88ρr/M；陣列雙程方向圖法線方向主瓣角度維與相控陣雷達一致，半功率寬度(對應于陣列角度分辨力)約為0.77λ0/(Md)。

2)米波OFDM-MIMO雷達具有明顯的多徑回波抑制能力，當天線高度ha和徑向距離RT滿足Δr1/2<ΔRs1條件時，因多徑與直達波路徑存在差別，其可在陣列法線方向實現對多徑回波的有效抑制，且隨頻偏B的增大，抑制能力進一步提升。

3)米波OFDM-MIMO雷達多脈沖回波存在多普勒單元走動現象，因通道維與脈沖維的耦合，使得脈沖維處理時需要考慮這一走動現象。