機械活化對黃鐵礦熱自燃動力學特性的影響*

陳姿霖

(中鋼集團武漢安全環保研究院有限公司，湖北 武漢 430080)

0 引言

煤自燃是目前煤礦安全生產面臨的重大難題[1-2]，自燃引起的火災一直威脅著礦山的安全生產，甚至造成人員傷亡。由于煤層中黃鐵礦含量較高，黃鐵礦易發生自燃[3]以及黃鐵礦中的無機硫使煤更易氧化[4-5]，嚴重縮短了煤自燃發火期，因而易引發煤礦火災。有研究表明,在開采過程中硫化礦石因受到不同形式的機械力作用而被活化，處于不穩定狀態，易發生氧化自燃反應[6]，因此研究機械活化及未活化的黃鐵礦的化學反應動力學機理尤為重要，可為研究黃鐵礦對煤自燃的影響提供理論依據。

熱分析是研究物質反應動力學的重要手段，應用廣泛。陽富強等[7]采用Coats-Redfern積分法求出硫化礦石在不同升溫速率下的活化能及指前因子，為硫化礦石自燃傾向性判定提供了依據；劉明強等[8]運用模式配合法和模式法對煤泥燃燒反應進行了動力學研究，推斷出煤泥燃燒的最概然反應機理函數；陳娟等[9]采用Friedman法得到了不同粒徑褐煤的動力學模型。然而不同的研究得到的動力學參數往往有很大差異，不僅與實驗條件、儀器、試樣有關，還與數據計算方法和反應機理的判別方法有關[10]。目前國際上推斷機理函數的方法很多，其中Malek法是國際熱分析和量熱學協會公認的一種方法[11]。

張燕娟等[12]采用攪拌球磨對鐵酸鋅進行了機械活化，發現鐵酸鋅活化后與硫酸反應的表觀活化能降低，化學反應活性提高；張有新等[13]研究發現，磁黃鐵礦經振動磨機械活化后表觀活化能降低，化學反應活性提高；張超等[14]研究了機械活化后黃鐵礦的儲能，也得到了機械活化后礦物的表觀活化能會降低的結論，但尚未考慮機械作用后礦物粒徑減小對表觀活化能的影響[15]。因此，本文提出了最概然Malek法和Achar-Brindley-Sharp-Wendworth法分析體系，通過計算分析，推斷出相近平均粒徑下機械活化及未活化黃鐵礦的機理函數以及動力學參數，并對得到的反應速率方程進行了驗證，以期為預測及防止煤層中黃鐵礦自燃提供理論依據。

1 實驗

1.1 制樣

黃鐵礦試樣取自安徽銅陵赫爾礦產品有限公司，采用Axios advanced X射線熒光光譜儀對試樣的化學成分進行了分析，結果表明，該黃鐵礦中ω(S)為 42.02%、ω(Fe)為 42.75%。

首先采用16目的標準篩篩分得到黃鐵礦樣品，再用200目標準篩篩分得到未活化的黃鐵礦(樣品1)，另用QM-BP型行星球磨機破碎黃鐵礦樣品5 min制備機械活化的黃鐵礦(樣品2)。

1.2 表征

采用Mastersizer 2000激光粒度儀測試樣品1和樣品2的平均粒徑，得到樣品的粒度累計分布(見圖1)。由圖1可知，樣品1和樣品2的平均粒徑相差不大。

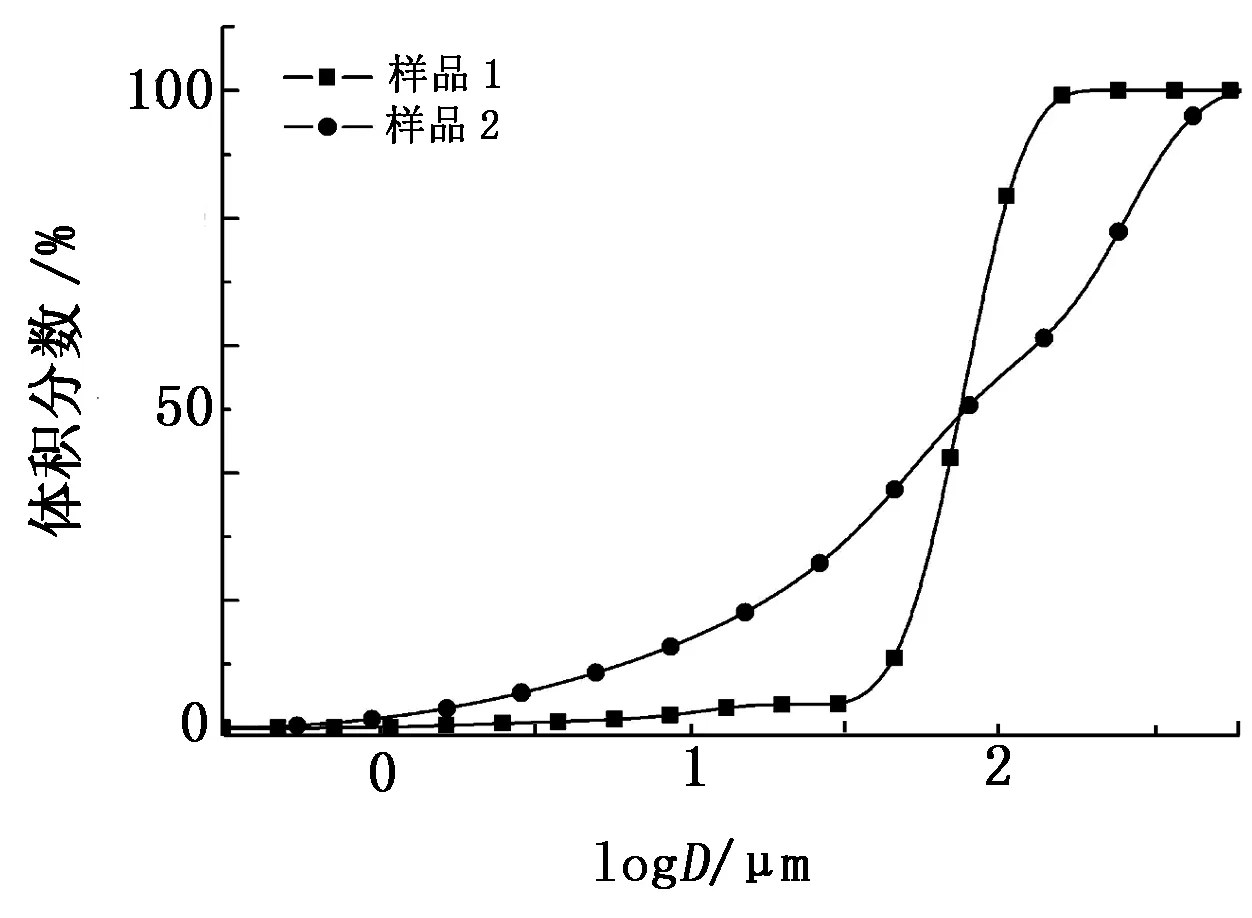
圖1 樣品的粒度累計分布(D為粒徑)

采用X射線衍射儀(D8 Advance型)對樣品的結構進行表征，分別得到樣品1和樣品2的X射線衍射(XRD)圖譜(見圖2)。使用MDI JADE5.0(XRD分析軟件)對樣品1和樣品2 的XRD圖譜的衍射峰進行分析擬合，得到樣品的晶粒粒徑和晶格畸變率(見表1)。由圖2和表1可知，黃鐵礦經機械活化后衍射峰強度寬化和增強，主要原因是機械活化導致黃鐵礦結構改變，活化后的黃鐵礦的晶粒粒徑減小，晶格畸變率增大。

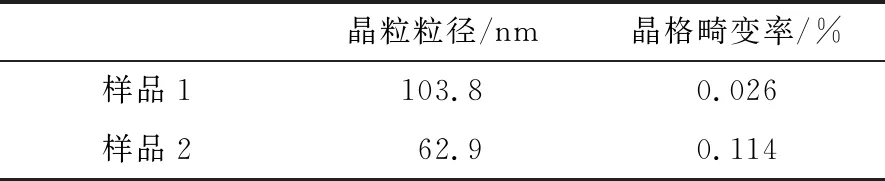
表1 黃鐵礦樣品的結構參數

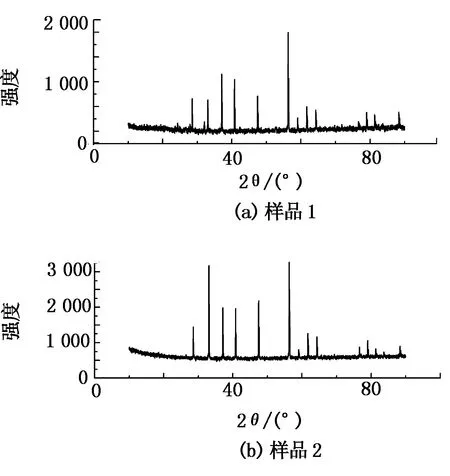
圖2 黃鐵礦樣品的XRD圖譜

運用掃描電子顯微鏡(JSM-5610LV型)對樣品1和樣品2的形貌和微結構進行表征，得到對應的SEM圖(見圖3)。

由圖3可知，機械活化后的黃鐵礦粒度分布不均勻，礦物晶面存在缺陷、畸變，且部分細化后的礦粒附著在大塊礦的表面。

1.3 實驗方法

取10 mg樣品1和樣品2分別在升溫速率為10、15、20 K/min，溫度范圍為50～800 ℃，以氮氣作為載氣，空氣流量為20 L/min的條件下，在STA6000同步熱分析儀中進行非等溫測試。

2 結果與討論

2.1 活化對TG-DSC曲線特性的影響

利用同步熱分析儀溫控程序得到樣品1和樣品2在10、15、20 K/min三種升溫速率下的TG-DSC曲線(見圖4和圖5)。

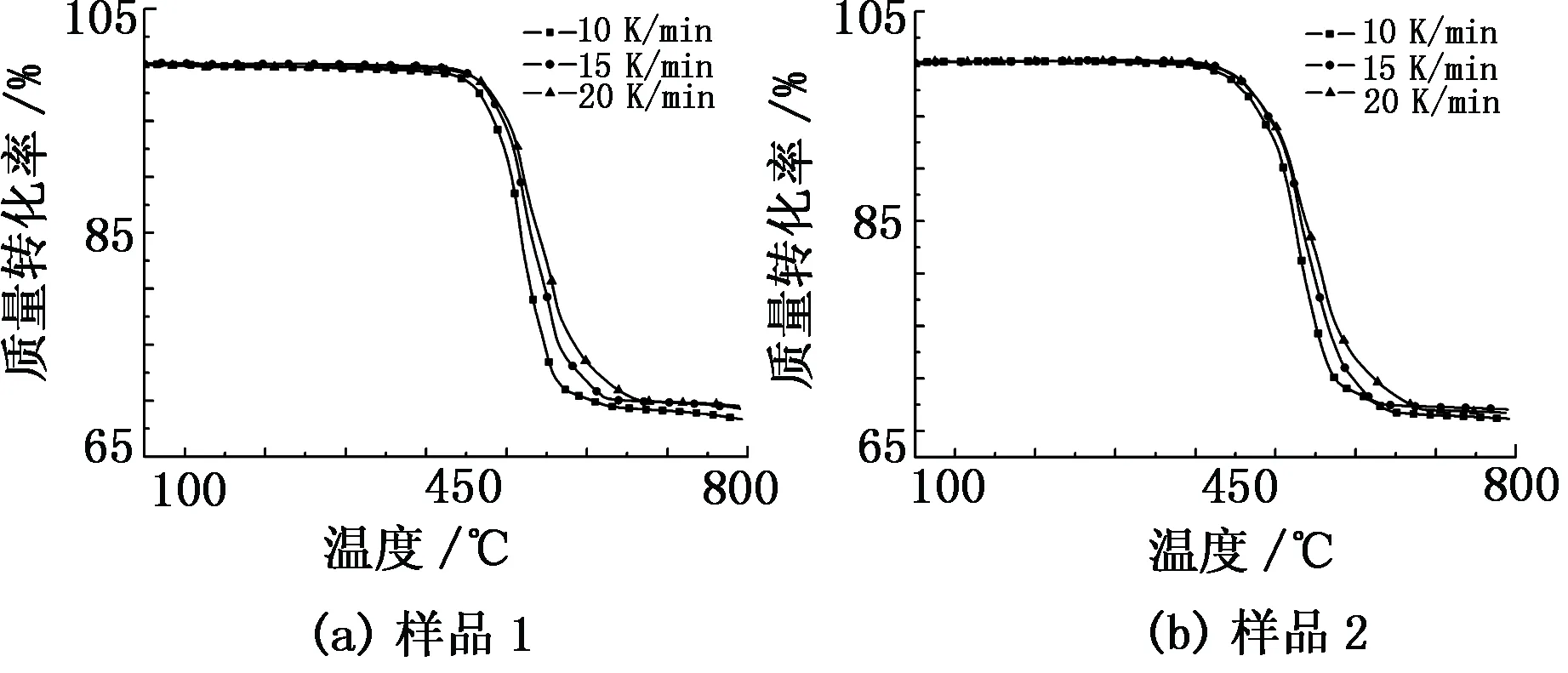
圖4 三種升溫速率下的TG曲線

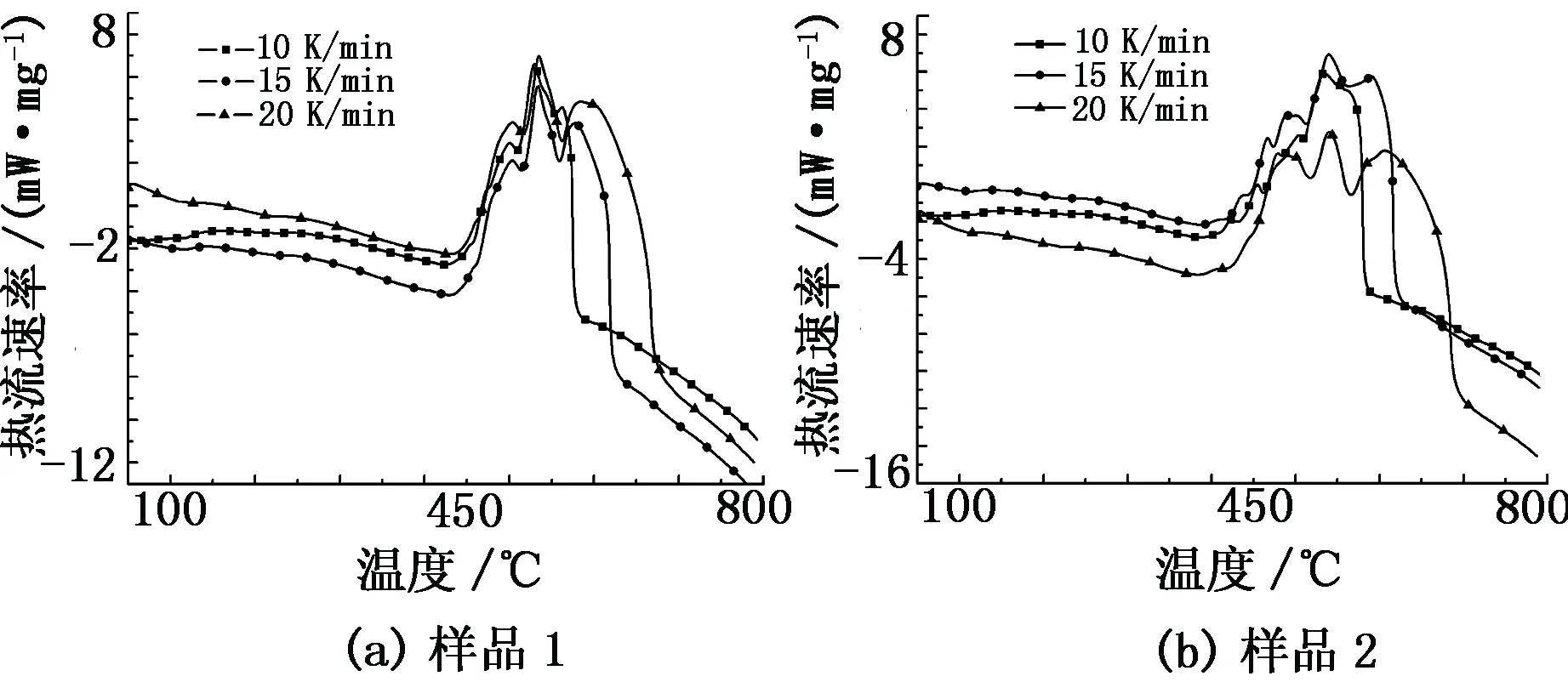
圖5 三種升溫速率下的DSC曲線

采用Pyris Manager軟件對機械活化前后黃鐵礦樣品的TG-DSC曲線進行分析，得到樣品1和樣品2在10、15、20 K/min三種升溫速率下的特征參數(見表2)。

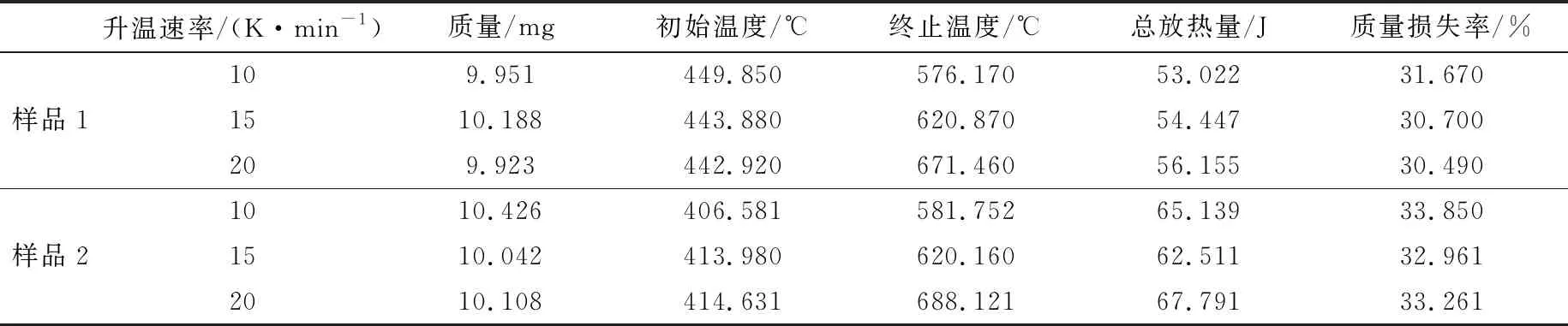
表2 樣品1、樣品2在三種升溫速率下的特征參數

由表2可知：機械活化后的黃鐵礦樣品初始溫度均低于未活化的黃鐵礦樣品，而兩者終止溫度相近，主要因為在兩者平均粒徑相近的條件下，經行星球磨機機械活化后的黃鐵礦結構發生了改變，在黃鐵礦晶體內部機械能以其他的形式存在，這導致機械活化后的黃鐵礦樣品更易發生氧化自燃反應，這與文獻[6]的研究結果一致；機械活化后黃鐵礦樣品的質量損失率和總放熱量均大于未活化的黃鐵礦，這說明在平均粒徑相近、質量相同的條件下，黃鐵礦經機械活化后的氧化自燃反應更加徹底，氧化產物的轉化率增大。

2.2 活化對黃鐵礦熱反應動力學影響分析

2.2.1 基于Malek法推斷最概然機理函數

黃鐵礦的氧化自燃反應屬于非均相反應，反應過程中包含多個平行、連續的基元反應，但為了便于分析黃鐵礦的氧化自燃反應的動力學規律，通常將復雜的反應過程簡單化，采用單一的反應機理函數模型描述黃鐵礦氧化自燃過程。本文將根據幾種常見的反應動力學機理函數的積分式和微分式[16](見表3)，結合Malek法[17]推斷機械活化前后黃鐵礦樣品氧化自燃反應的最概然機理函數。

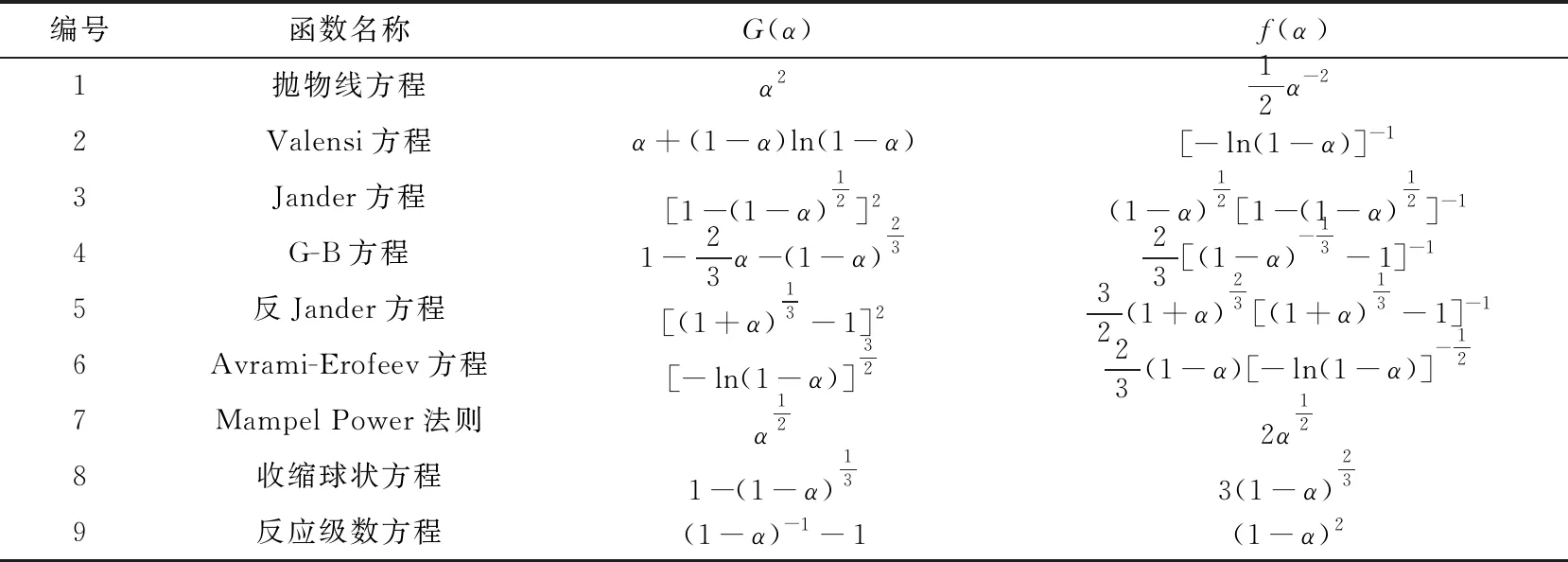
表3 常見的機理函數

(1)

將人為數據：αi，y(αi)，i=1,2,…和α=0.5， 代入式(1)，得到y(α)-α關系曲線，視其為標準曲線。

(2)

將實驗數據：αi，Ti，(dα/dt)i，i=1,2,…和α=0.5，T0.5,(dα/dt)0.5代入式(2)，作y(α)-α關系曲線，視其為實驗曲線。

若標準曲線與實驗曲線偏差最小，則認為該標準曲線對應的機理函數為最概然機理函數。

以上公式中涉及的T為溫度，α為反應轉化率，i為選取的轉化率數量。

將表3中9種常見的機理函數的微分形式f(α)和積分形式G(α)代入式(1)，計算得到標準曲線；將樣品1和樣品2的實驗數據代入式(2)，得到樣品在10、15、20 K/min三種升溫速率下的實驗曲線。運用Origin軟件計算實驗曲線和標準曲線的偏差，根據偏差的大小確定最概然機理函數。

以未活化的黃鐵礦樣品1在10、15、20 K/min三種升溫速率下的實驗數據為例進行計算，其y(α)-α實驗曲線和標準曲線的對比見圖6。

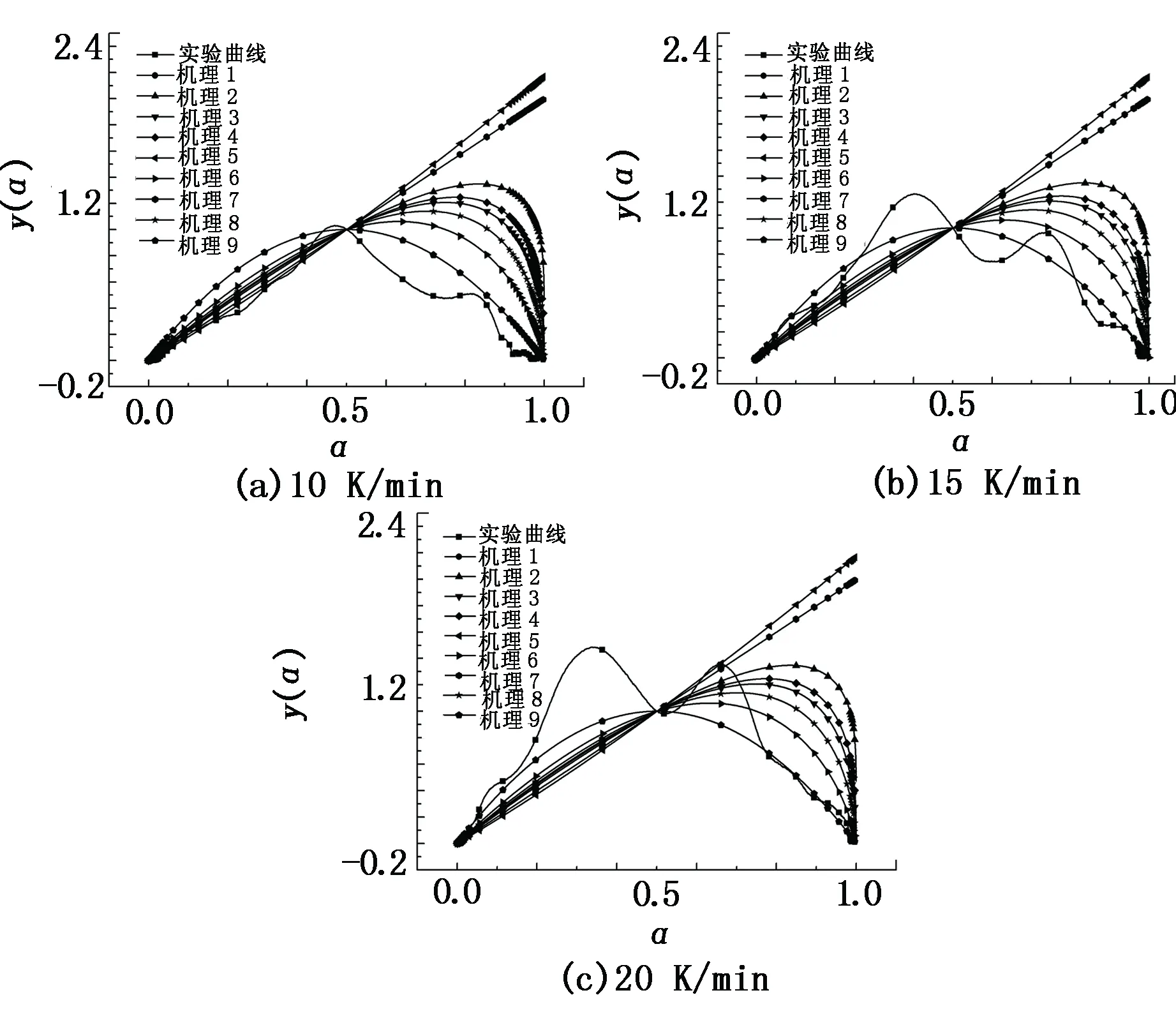
圖6 樣品1在三種升溫速率下的y(α)-α曲線

由圖6可知，樣品1在三種升溫速率下得到的實驗曲線與機理函數9的標準曲線偏差最小，且偏差值隨著升溫速率的增大而減小。同理可證，對機械活化后的黃鐵礦樣品2在三種升溫速率下的實驗數據進行處理分析，得到的實驗曲線同樣與機理函數9的標準曲線偏差最小，表明機械活化前后的黃鐵礦氧化自燃反應最概然機理函數均為反應級數方程f(α)=(1-α)2。

2.2.2 基于Achar-Brindley-Sharp-Wendworth法求解動力學參數

Achar微分法的方程為

(3)

式中，E為活化能，A為指前因子，R為氣體常數。

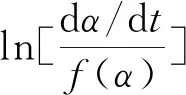
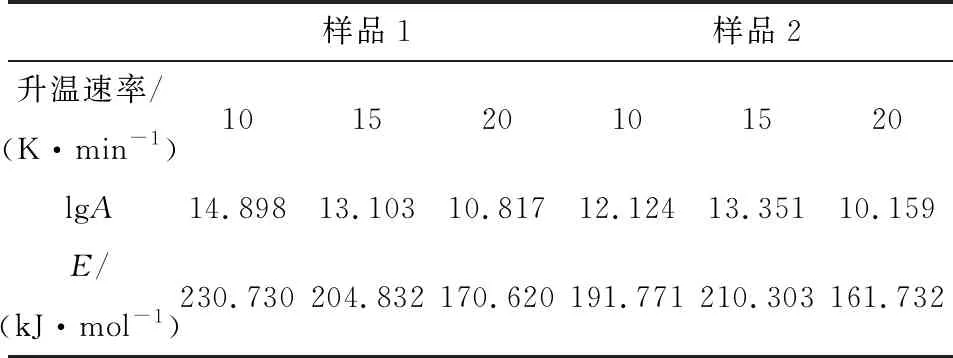
表4 樣品1和樣品2在三種升溫速率下的動力學參數

對比表4中樣品1和樣品2的活化能可知，機械活化后黃鐵礦在10、20 K/min升溫速率下的活化能較未活化的黃鐵礦小，而在15 K/min升溫速率下兩者活化能相近，表明在平均粒徑相近的條件下，機械活化后的黃鐵礦更易發生氧化自燃反應，即黃鐵礦經機械活化后常態分子轉化為活躍狀態的分子，繼而發生反應所需要的能量相比未活化的小，這與文獻[6]研究結果一致。且樣品1和樣品2平均粒徑相近，在排除粒徑對黃鐵礦活化能影響的前提下，機械活化后的黃鐵礦活化能降低的主要原因是在機械力的作用下黃鐵礦晶格發生畸變、晶粒粒徑減小。

2.2.3 動力學模型驗證

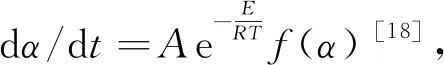
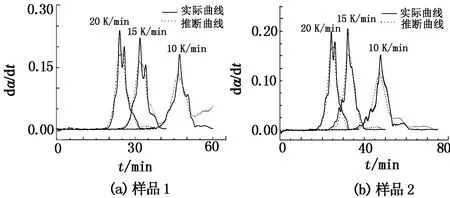
圖7 三種升溫速率下實際曲線與推斷曲線的比較

由圖7可知，用所求的最概然機理函數得到的計算曲線與實驗曲線吻合度較好，且計算曲線和實驗曲線隨著升溫速率的增加兩者的偏差減小，該結果驗證了反應機理函數f(α)=(1-α)2的準確性，表明該機理函數反應速率方程可以合理描述機械活化及未活化的黃鐵礦的氧化自燃反應過程。

3 結論

a.通過對比機械活化前后的黃鐵礦在10、15、20 K/min三種升溫速率下的TG-DSC曲線，發現在平均粒徑相近、質量相同的條件下，機械活化后的黃鐵礦反應的初始溫度較低，而最終轉化率較高。

b.用Malek法推斷出機械活化及未活化的黃鐵礦的最概然機理函數均為f(α)=(1-α)2，且升溫速率越高，標準曲線與實驗曲線偏差越小，即反應機理為f(α)=(1-α)2的可能性越大。用Achar微分法分析相近粒徑條件下活化及未活化的黃鐵礦的動力學參數，排除了機械活化后粒徑對黃鐵礦的影響后，活化能相差較小，其主要原因是機械作用導致晶格發生了變化。

c.通過動力學模型驗證發現，用Malek法求得的機械活化及未活化的黃鐵礦的最概然機理函數對應的計算曲線與實驗曲線吻合較好，表明該方法得到的機理函數可以合理描述機械活化及未活化的黃鐵礦的氧化自燃過程。