基于改進Jensen不等式的中立型時滯系統穩定性判據

楊明明， 邵 荃，丁 嘯

（1.南京航空航天大學民航學院，南京 210016；2.上海農村商業銀行總行，上海 201210）

時滯現象是引起系統振動和不穩定的關鍵因素，在工業過程、神經網絡等實際生產生活中隨處可見.近年來，許多學者對于時變時滯系統的區間顯著性過程進行了大量的研究.He等［1］推動了最初的區間變時滯的發展，確定了基本的穩定性判據，并在文獻［2］通過自由權矩陣方法，提出了有關區間時變時滯的神經網絡更低保守性的研究成果.文獻［3-7］使用的自由權矩陣方法和Jensen積分不等式對時滯系統穩定性進行進一步研究.文獻［8-11］通過結合構造新的Lyapunov函數進一步改善了時滯系統的穩定性結論.彭丹和華長春［12］通過引入2-D Jensen不等式并結合Lyapunov函數給出了新的時滯系統穩定性準則.孫欣、高躍［13-14］將Writinger積分不等式應用于時滯系統，證明其與Jensen不等式相比有更低的保守性.

本文基于現有時滯系統的研究成果，通過將Jensen不等式轉化為保守性更低的Wirtinger型不等式，并構建新的Lyapunov-Krasovskii泛函，結合自由權矩陣得到了基于線性矩陣不等式形式（Linear matrix inequality，LMI）的時滯系統漸近穩定性的新判據并進行了證明.

1 基本概念

1.1 Jensen不等式

Jensen不等式是反映凸函數的基本不等式，對于任意常數矩陣M∈Rm×m，M=MT>0，標量γ>0，向量函數[0 ,γ]→Rm有以下Jensen積分不等式：

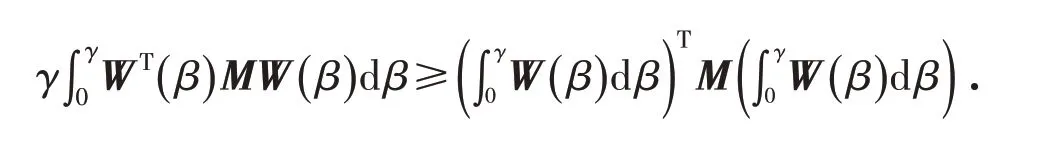
1.2 Wirtinger型不等式

與Jensen不等式相比，Wirtinger不等式的保守性更小［13］.因此本文對Jensen不等式進行改進，得到新的Wirtinger型不等式.

Wirtinger不等式的形式為：對于任意常數矩陣M∈Rm×m，M=MT>0，向量函數[0 ,γ]→Rm有：

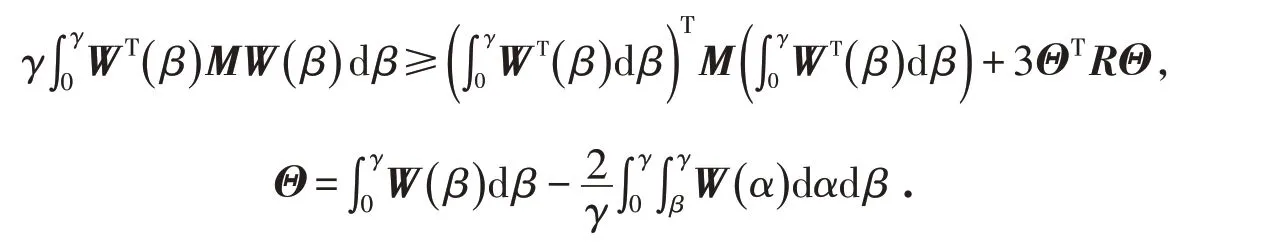
1.3 自由權矩陣

利用Park不等式或Moon不等式結合模型變換是解……