基于數(shù)學(xué)運(yùn)算素養(yǎng)下“立體幾何初步”的教學(xué)
——“直觀圖畫法”課堂教學(xué)設(shè)計(jì)與感悟

江蘇 鄭寶生 鄧 蓉

數(shù)學(xué)運(yùn)算是數(shù)學(xué)活動(dòng)的基本形式,也是一種演繹推理.數(shù)學(xué)運(yùn)算是指在明晰運(yùn)算對(duì)象的基礎(chǔ)上,依據(jù)運(yùn)算法則解決數(shù)學(xué)問題的素養(yǎng).它不只是數(shù)字或字母的運(yùn)算,主要表現(xiàn)為:理解運(yùn)算對(duì)象,掌握運(yùn)算法則,探求運(yùn)算思路,求得運(yùn)算結(jié)果.它有助于促進(jìn)數(shù)學(xué)思維發(fā)展,形成一絲不茍、嚴(yán)謹(jǐn)求實(shí)的科學(xué)精神.立體幾何是研究點(diǎn)、線、面及其位置關(guān)系的,重點(diǎn)在于培養(yǎng)學(xué)生的空間想象能力,在“立體幾何初步”教學(xué)中如何落實(shí)數(shù)學(xué)核心素養(yǎng),立足于數(shù)學(xué)運(yùn)算的視角下怎樣設(shè)計(jì)課堂教學(xué),值得我們思考.本文結(jié)合“直觀圖畫法”的課堂教學(xué)設(shè)計(jì)談一談個(gè)人的看法.

一、數(shù)學(xué)內(nèi)容分析

立體幾何是研究現(xiàn)實(shí)世界物體的形狀、大小和位置關(guān)系的,而“立體幾何初步”的學(xué)習(xí),恰恰是為學(xué)生提供立體幾何方面的知識(shí)基礎(chǔ),探求解決立體幾何問題的方式方法以及公理化體系.而“直觀圖畫法”是學(xué)習(xí)立體幾何的初級(jí)門檻,它為“立體幾何”的后續(xù)學(xué)習(xí)建立了立體圖形的保障.

二、學(xué)情分析

學(xué)生從小學(xué)開始就認(rèn)識(shí)長方體和正方體,接下來了解圓錐和球體,到了初中學(xué)習(xí)了幾種常見的幾何體并求其面積和體積,學(xué)習(xí)了三視圖并通過三視圖來確定幾何體,這給了學(xué)生畫立體圖形以豐富的感性知識(shí),為本節(jié)課內(nèi)容的學(xué)習(xí)奠定了良好的基礎(chǔ).其實(shí),對(duì)于大部分學(xué)生來說,他們?cè)诔踔芯鸵呀?jīng)會(huì)畫長方體和正方體的直觀圖,然而他們并不理解每一步操作的合理性,更沒有在實(shí)際操作中形成優(yōu)化的、完整的操作程序,所以說對(duì)于“直觀圖畫法”的學(xué)習(xí)既需要思想認(rèn)識(shí)上的理解,又需要實(shí)際操作上的掌握.本課施教學(xué)生是一所普通高中三星級(jí)學(xué)校的學(xué)生,基礎(chǔ)和接受能力不夠強(qiáng).

三、教學(xué)策略分析

從教學(xué)目標(biāo)上看,通過情境中的學(xué)生活動(dòng),增加學(xué)生的感性認(rèn)知;通過問題的提出,探求畫水平放置的平面圖形的直觀圖的合理性;通過數(shù)學(xué)運(yùn)用,探求任意多邊形與其直觀圖面積的關(guān)系;通過歸納整理,求得立體幾何圖形的斜二測(cè)畫法.從教學(xué)方式上,在直觀感知的基礎(chǔ)上進(jìn)行操作確認(rèn),在度量計(jì)算的基礎(chǔ)上探求結(jié)論,在推理證明的基礎(chǔ)上形成規(guī)律.從教學(xué)重點(diǎn)和難點(diǎn)的角度出發(fā),重點(diǎn)是掌握幾何體的斜二測(cè)畫法,難點(diǎn)是平面圖形與其直觀圖之間的關(guān)系.根據(jù)上述學(xué)情,側(cè)重于基礎(chǔ),過程教學(xué)做得比較細(xì).

四、教學(xué)過程

教材采用“蘇教版《普通高中課程標(biāo)準(zhǔn)實(shí)驗(yàn)教科書·數(shù)學(xué)》必修2,第一章立體幾何初步,§1.1.4直觀圖畫法”.

1.問題情境 學(xué)生參與活動(dòng)

(1)出示一個(gè)實(shí)物正方體,要求每個(gè)學(xué)生都把這個(gè)正方體畫出來,其中讓兩個(gè)學(xué)生板演;

(2)讓學(xué)生相互點(diǎn)評(píng),并嘗試提出問題.

【意圖】由于小學(xué)和初中的知識(shí)基礎(chǔ),學(xué)生能畫出正方體和長方體立體圖形,然而他們并不知道為什么要這樣畫？當(dāng)然也沒有一定的操作流程.

2.提出問題 理解運(yùn)算對(duì)象

問題1:正方體的主視(面)為什么畫成正方形,而上下底面要畫成平行四邊形？

【意圖】當(dāng)學(xué)生自己畫出正方體的立體圖形,但不知道為什么這樣操作,這樣就產(chǎn)生了認(rèn)知上的沖突,能更好地激發(fā)學(xué)生探求其中奧妙的學(xué)習(xí)熱情.

事實(shí)上,給學(xué)生出示一張正方形紙片,把正方形豎直放置,按照我們看到的原樣畫出,而水平放置的正方形我們看到的是一條線段,這條線段無法表達(dá)它是水平放置的正方形,所以我們需要找到一個(gè)好的視角來觀察水平放置的正方形,只要站在水平放置的正方形的一個(gè)角的上方來觀察它,按照近大遠(yuǎn)小的透視規(guī)律,故用平行四邊形表達(dá).

問題2:水平放置的正方形我們用平行四邊形來表示,畫這樣的平行四邊形有怎樣的要求？長與寬的線段各畫多少？其銳角應(yīng)該是多少度？

【意圖】引導(dǎo)學(xué)生思考,從觀察的角度看,其長度不變,而寬度取其一半比較容易計(jì)算,同樣角度也取其一半為45°,由于同旁內(nèi)角互補(bǔ)也可以是135°.

問題3:畫一個(gè)正方形或平行四邊形的關(guān)鍵都是確定四個(gè)頂點(diǎn)的位置,我們會(huì)用怎樣的方式來確定平面內(nèi)的點(diǎn)的位置？

【意圖】學(xué)生會(huì)畫正方形和平行四邊形,但他們不一定意識(shí)到,畫正方形和平行四邊形其實(shí)是確定四個(gè)頂點(diǎn)的位置,由于學(xué)生能夠聯(lián)想到平面內(nèi)確定點(diǎn)的位置可以建立平面直角坐標(biāo)系,類似地畫水平放置的正方形的直觀圖,需要建立夾角為45°或135°的斜坐標(biāo)系.

3.展示例題 掌握運(yùn)算法則

例1.畫水平放置的正三角形的直觀圖.

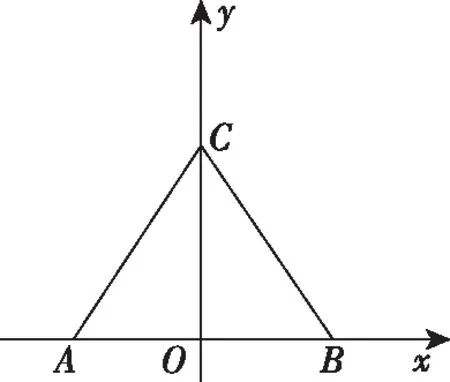
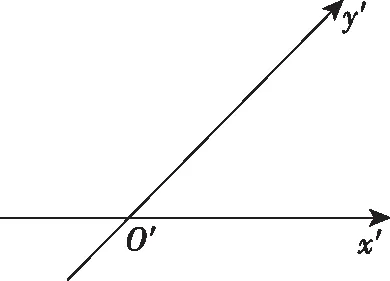
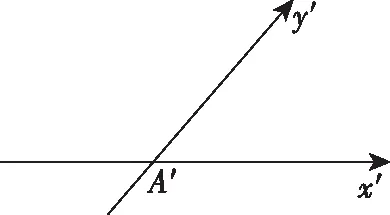
(2)建立平面的斜坐標(biāo)系,如圖2,使∠x′O′y′=45°或135°,寫出對(duì)應(yīng)點(diǎn)O′,A′,B′,C′的坐標(biāo)分別為O′(0,0),A′( ),B′( ),C′( ),并描出三個(gè)點(diǎn).

(3)連接A′C′和B′C′,則三角形△A′B′C′就是△ABC水平放置的直觀圖.

【回顧】①請(qǐng)把上述的操作過程用語言敘述一遍;

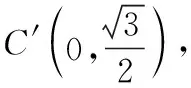
③點(diǎn)P(1,2)在直觀圖中對(duì)應(yīng)的點(diǎn)P′的坐標(biāo)是什么？任意點(diǎn)Q(x,y)在直觀圖中的對(duì)應(yīng)點(diǎn)Q′的坐標(biāo)是什么？

【意圖】通過學(xué)生的口述,讓學(xué)生提煉操作流程,然后通過與平面直角坐標(biāo)系的類比形成斜坐標(biāo)系,重點(diǎn)在于讓學(xué)生理解斜坐標(biāo)系下點(diǎn)的坐標(biāo),這是學(xué)生第一次接觸的問題,所以在回顧中進(jìn)行了加強(qiáng),特別是斜坐標(biāo)的幾何意義,斜坐標(biāo)中的兩個(gè)數(shù)的絕對(duì)值代表哪條線段的長度是關(guān)鍵.

4.數(shù)學(xué)探究 探求運(yùn)算思路

問題4:學(xué)生練習(xí),畫出下列圖形水平放置的直觀圖.

(1)邊長為2的正三角形ABC,如圖3;

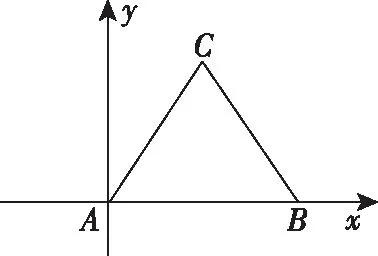
(2)底角為45°的等腰梯形ABCD,其中AB=6,CD=2,如圖4.

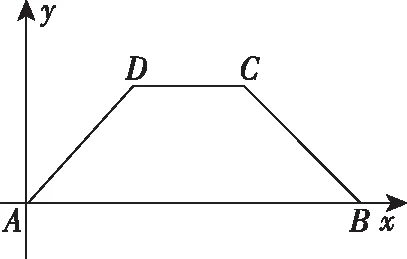
圖4

【回顧】①在上述第一個(gè)問題中關(guān)鍵畫出哪個(gè)點(diǎn)？你能發(fā)現(xiàn)△ABC與其直觀圖△A′B′C′及其對(duì)應(yīng)的元素有怎樣的關(guān)系？

②在上述第二個(gè)問題中關(guān)鍵畫出哪些點(diǎn)？等腰梯形ABCD與其直觀圖梯形A′B′C′D′及其對(duì)應(yīng)的元素有怎樣的關(guān)系？

③從上述兩個(gè)問題中,你可以發(fā)現(xiàn)怎樣的結(jié)論？并給出證明.

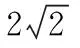
5.歸納整理 形成運(yùn)算程序

例2.畫棱長為2 cm的正方體ABCD-A1B1C1D1的直觀圖.

畫法:(1)以互相垂直的AB為x軸,AD為y軸,AA1為z軸,在正方體ABCD-A1B1C1D1上建立空間直角坐標(biāo)系;

(2)畫其直觀圖中對(duì)應(yīng)的x′軸,y′軸和z′軸,它們相交于A′,使∠x′A′y′=45°或135°,∠x′A′z′=90°,如圖,建立空間的斜坐標(biāo)系;

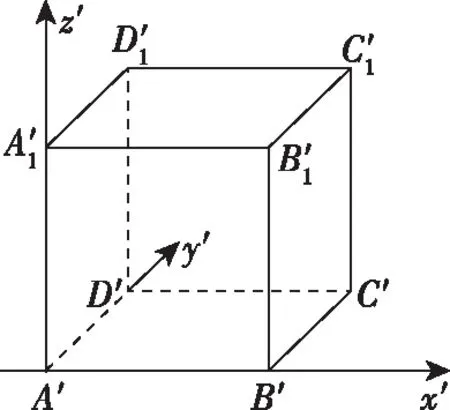
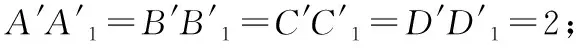
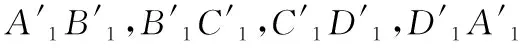
【回顧】①口述上述操作過程,并與例1作比較.

②上述畫直觀圖的方法叫作斜二測(cè)畫法,你認(rèn)為這里的“斜”是指什么？“二測(cè)”又是指什么？

③請(qǐng)歸納直觀圖斜二測(cè)畫法的規(guī)則.

【意圖】通過兩個(gè)例題的比較容易發(fā)現(xiàn)其共同之處,都需要建立對(duì)應(yīng)的兩種不同的坐標(biāo)系,對(duì)于平面圖形,斜是指y′軸相對(duì)于x′軸所成角45°或135°，是斜的,二測(cè)是指平行于x軸的線段在其直觀圖中平行于x′軸,且長度不變;平行于y軸的線段在其直觀圖中平行于y′軸,且長度變?yōu)樵瓉淼囊话?如果是立體圖形,再追加一個(gè)條件,平行于z軸的線段在其直觀圖形中平行于z′軸,且長度不變.這樣學(xué)生更容易歸納出斜二測(cè)畫法的操作規(guī)則.

6.回顧反思 求得運(yùn)算結(jié)果

(1)兩種方法:①畫圖關(guān)鍵在于描點(diǎn),怎樣把點(diǎn)取得更準(zhǔn)確,建立坐標(biāo)系;②直觀圖的斜二測(cè)畫法規(guī)則;

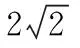
五、三點(diǎn)感悟

從育人的角度看,數(shù)學(xué)課堂教學(xué)要揭示數(shù)學(xué)本質(zhì),開展數(shù)學(xué)探究,提升學(xué)生的數(shù)學(xué)素養(yǎng).其一,展示知識(shí)的產(chǎn)生過程,揭示數(shù)學(xué)的本質(zhì).對(duì)于高中生來說會(huì)畫正方體,但是不知道為什么這樣畫,更不知道像寫漢字一樣還要有一個(gè)先后的次序、優(yōu)化的程序,正所謂知其然不知其所以然,所以我們需要學(xué)生在嘗試畫正方體中提出問題,在問題的解決過程中形成操作的合理性和必然性.畫平面圖形的直觀圖關(guān)鍵是確定點(diǎn)的位置,如何確定點(diǎn)在平面的位置,通過直角坐標(biāo)系建立對(duì)應(yīng)的斜坐標(biāo)系,在斜坐標(biāo)系中找出點(diǎn)的位置才是畫直觀圖的本質(zhì),這也是學(xué)生最熟悉、最容易理解的.