從一道圓錐曲線焦點分弦題談二級結論的巧用

甘肅 何少杰

二級結論源于教材中的基礎知識,它是利用基本概念、基本定理,經過歸納、推理、證明,總結出來的結論;它是特定條件下一些解題步驟的有序整合.

圓錐曲線是高中階段解析幾何的重要內容,坐標法建立了方程與曲線之間的聯系,為“數形結合”架起了橋梁.雖然在教學中我們一直強調通性通法,但在解答選擇題或者填空題時,如果利用通性通法聯立方程,就可能會陷入繁雜的運算,如果能夠靈活地利用好二級結論,就可以規避掉大量重復的計算,節省時間,提高解題效率,巧妙地解決問題.在高考中,焦點弦問題是圓錐曲線考查中的熱點,圓錐曲線中的二級結論很多,下面以一道示范性較強的焦點分弦問題為例,通過多種解法對比,來說明利用圓錐曲線中常用的二級結論解決問題的高效性,體會由一題多解到多解歸一的過程.

一、試題呈現

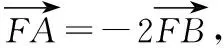
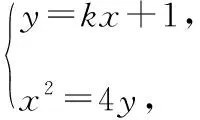
評析:代數方法求解此題時,為避免反復計算,使用韋達定理與向量知識整合是一種不錯的方法,而且也是通性通法,但這樣的解答并無亮點,有些同類題目可能運算量會比較大,浪費時間.

解法2:

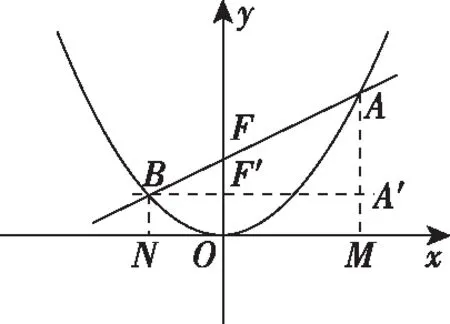
評析:本題雖然使用了數形結合的方法,但未找到解題的捷徑,顯然比較煩瑣.

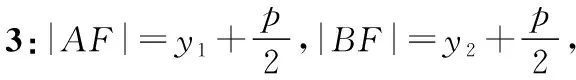
評析:這一解法使用了兩個公式:焦半徑公式、弦長公式,解法很有技巧,滲透了函數與方程思想,與圓錐曲線中常用的設而不求方法,看似巧妙,但事實上仍是通性通法的靈活運用,雖然回歸了定義,但仍顯煩瑣,除了函數方程思想外,解析幾何還講究“數形結合”,巧妙使用平面幾何知識往往能加快解題速度.

評析:借助圓錐曲線的第二定義,同時使用了數形結合的方法,直觀易懂,在解決選擇、填空一類題型時較好.

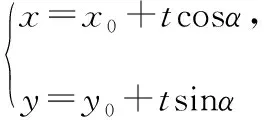
得cos2α·t2-4sinα·t-4=0,

設|AF|=|t1|,|BF|=|t2|,可知t1>0,t2<0,t1=-2t2.

評析:以上解法除解法1外,其余方法技巧性較強,不是通性通法,適用范圍受到限制,而解法1為通性通法,以代數方法為主,運算較為煩瑣,解法4是最為巧妙的方法,那么能否借助解法4找到一種普遍使用的公式解決圓錐曲線中焦點分弦一類問題呢?

二、利用二級結論,高效解題

以此題為背景,對圓錐曲線進行進一步的探索,利用已有的二級結論,獲得求解焦點分弦一類題型的一般性方法,從而有效避免繁雜的計算.

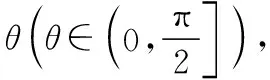
1.對于橫向型圓錐曲線

2.對于縱向型圓錐曲線

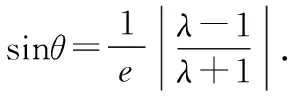
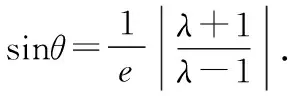
下面對這一二級結論進行證明.

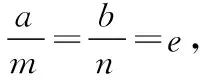
1.對于橫向型圓錐曲線

(1)當焦點F內分弦AB時,以橢圓為例進行證明:

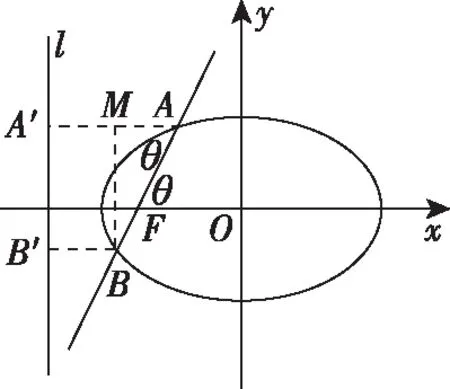
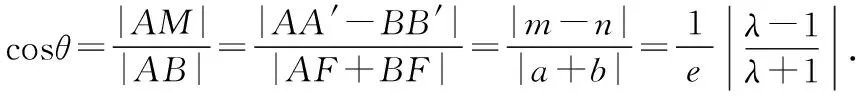
(2)當焦點F外分弦AB時,此時曲線為雙曲線.

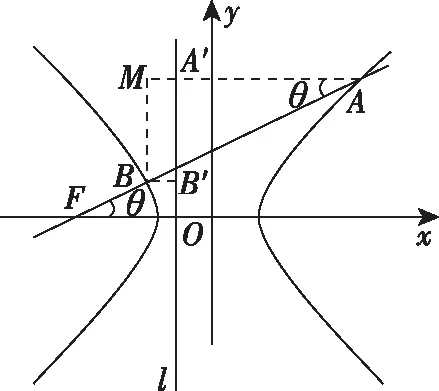
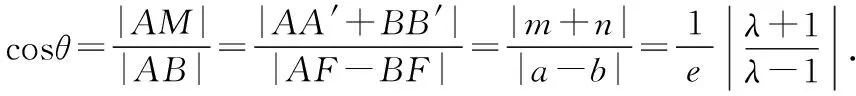
2.對于縱向型圓錐曲線

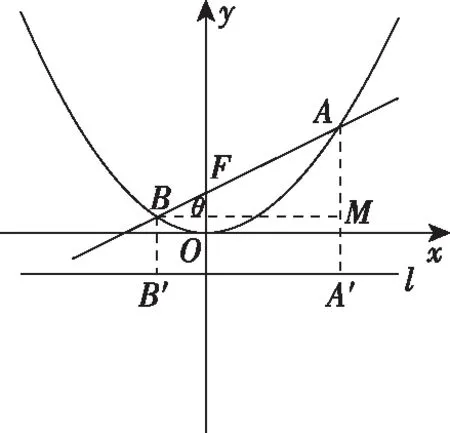
(2)當焦點F外分弦AB時,曲線為雙曲線.

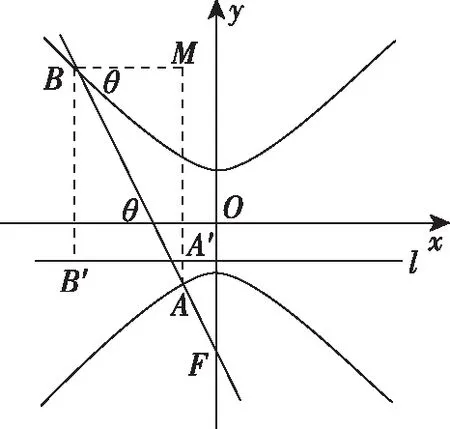
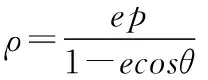
根據圓錐曲線的極坐標方程易得以下結論:

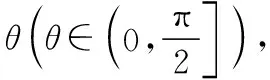
1.對于橫向型圓錐曲線

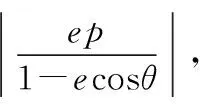
2.對于縱向型圓錐曲線

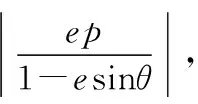
這一結論的證明這里不再贅述.結論1,2揭示了圓錐曲線焦點分弦的一些性質及特征,對于求解圓錐曲線中焦點分弦一類問題大有裨益,不妨運用結論1,2,繼續求解此題.

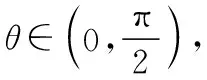
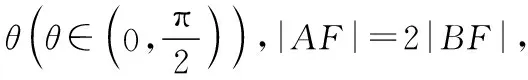
評析:與前面五種解法相比,結論1,2的使用大大的減少了此類題目的運算量,可以起到化繁為簡的作用,達到事半功倍的效果,而且也是求解此類題目的統一簡解,是通性通法的使用.