水平井眼中單彎螺桿鉆具組合力學分析方法*
黃 壯 侯作富 陳 錕 夏成宇 錢利勤 王 鵬 王旭東
(1. 長江大學機械工程學院 2. 中石油西南油氣田分公司頁巖氣研究院)
0 引 言
單彎螺桿鉆具組合比傳統鉆具組合具有更強的造斜能力,因此廣泛用于定向井造斜段的鉆進。單彎螺桿鉆具組合在連續滑動鉆進過程中,為實現單彎螺桿下部鉆具組合結構參數優化進而提高鉆具的造斜能力,也為滿足井眼軌跡控制要求,需要對單彎螺桿下部鉆具組合進行力學分析[1-3]。
多年來,諸多學者對下部鉆具組合建立了大量的力學模型。李子豐等[4-5]采用加權殘差法建立了下部鉆具組合三維小撓度靜力學分析數學模型。蘇義腦等[6]提出等效載荷法,分析了初彎曲對梁柱的影響。唐雪平[7-8]分析了受縱橫彎曲載荷聯合作用下的變剛度梁柱問題,可解決井斜控制實踐中不等截面尺寸梁柱問題。潘仁杰[9]建立了螺桿鉆具組合控制井斜力學模型。游云武[10]根據縱橫彎曲梁理論,建立了“單彎雙穩”鉆具鉆頭側向力模型。肖云峰等[11]采用有限元分析方法建立了單彎螺桿鉆具組合下部結構的力學模型。郭宗祿和高德利等[12-13]建立了底部鉆具組合復合鉆進導向力的擬動態計算模型,采用加權殘差法和牛頓-拉夫遜迭代法計算了底部鉆具組合變形的n個線性效應,并提出了預測鉆具組合性能的基本方程。尹虎等[14]根據有限元法把鉆具組合看作梁單元,建立了下部鉆具組合力學模型。FENG T.H.等[15]提出一種動態有限元模型,該模型通過沿井中心軸線性化問題來描述定向鉆井動力學。華勇[16]根據縱橫彎曲法建立了變剛度梁柱力學模型,可求解鉆井實際中常見的變剛度問題。
但上述研究在簡化處理時通常將彎角處理為連續梁、多變截面處理為等剛度,這樣勢必造成計算不準確。針對此類不連續和多剛度問題,本文利用微元法和連續梁理論建立了單彎螺桿下部鉆具組合統一力學模型,該模型對于單彎螺桿下部鉆具組合帶有多彎角和多變截面(多剛度)的問題,推導了一種可以直接計算的方法,使得分析結果更接近真實情況。研究成果可為單彎螺桿下部鉆具組合管柱的優化設計提供理論支撐。
1 單彎螺桿鉆具組合統一力學模型的建立
1.1 基本假設
單彎螺桿下部鉆具組合在水平段導向鉆進工況下的受力情況十分復雜,為了對鉆具組合的實際工作狀態進行受力分析,本文做以下基本假設:
(1)下部鉆具組合之間的變形是彈性小變形。
(2)鉆壓作用于鉆頭中心,鉆頭中心位于井眼軸線上。
(3)井壁視為剛性體,井眼直徑為鉆頭外徑且無井眼尺寸的變化。
(4)穩定器與井璧之間為點接觸。
(5)上切點以上鉆柱因自重貼在下井壁上。
1.2 單彎螺桿節點劃分及微元體受力分析
對于定向井段的作業,通常采用單彎螺桿進行導向鉆進。為滿足井眼軌跡的要求,首先要分析單彎螺桿下部鉆具組合的力學性能。本文根據單彎螺桿下部鉆具組合的各類形式,以鉆頭、變截面、管柱彎點、穩定器和上切點作為節點,對單彎螺桿下部鉆具組合進行跨段劃分,相鄰的兩個節點之間為一跨,單彎螺桿下部鉆具組合可以看作是由這些節點任意組合成的多跨梁柱。根據縱橫彎曲法對單彎螺桿下部鉆具組合的處理方法,將鉆頭至上切點處的鉆具組合簡化為梁柱進行受力及變形分析。
圖1為單彎螺桿下部鉆具組合示意圖。在梁柱的任意位置取長為dx的微元,其受力分析如圖2所示。

1—鉆頭;2、4、5—螺桿;3—穩定器;6、8—鉆鋌;7—扶正器;9—加重鉆鋌。

圖2 微元體受力分析圖Fig.2 Force analysis of infinitesimal body
在微元體受力分析圖中,在豎直方向求力學平衡,并以B截面中心為基準對z軸求力矩平衡,列平衡方程如下:
T+dT-T+qdx=0
(1)
(2)
式中:P為軸向載荷,kN;T為截面剪力,kN;Mz為截面彎矩,kN·m;q為均布載荷,kN;dy為微元體A端面中心與B端面中心的高度差,m。
(3)

(4)
式中:EI為梁柱的抗彎剛度,kN·m2。
對式(4)求通解,得梁柱的撓曲變形方程:

(5)
式中:x為微元體軸向長度的自變量,m;y為x處的撓度,m;C1~C4為各項的系數。
根據式(5)求出梁柱的轉角θ、彎矩M和剪力Q的計算公式:
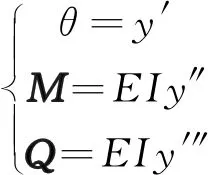
(6)
式中:y′、y″、y′″分別為y的一階導數、二階導數和三階導數。
1.3 各節點處的力學條件和矩陣表達式
圖3為包含各節點的單彎螺桿下部鉆具組合簡圖。圖3中:①為鉆頭,②為變截面,③為穩定器,④為管柱彎點,⑤為上切點。根據圖示各節點對該單彎螺桿下部鉆具組合進行跨段劃分,再結合各節點處的邊界條件、連續性條件和位移條件求得各節點處的矩陣表達式。為了清楚地描述出各節點處的矩陣表達式,建立如圖3右上角所示的坐標系,任取相鄰兩跨梁柱,在每跨梁柱的左端點各建立一個平面直角坐標系,其中,xi為前一跨梁柱長度的自變量,yi為xi處對應的撓度,xj為后一跨梁柱長度的自變量,yj為xj處對應的撓度。

圖3 包含各節點的單彎雙穩螺桿下部鉆具組合簡圖Fig.3 Schematic diagram for single-bend and double-stabilizer PDM assembly containing all nodes
1.3.1 鉆頭
如圖3所示,鉆頭處的邊界條件為:鉆頭處梁柱撓度為0、鉆頭彎矩為0;表達式為:xi=0,yi=0;xi=0,Mi=0。其中Mi為xi處對應的彎矩;由于鉆頭前無梁柱,即xi=0,此處yi代表鉆頭處撓度,Mi代表鉆頭處彎矩。
聯立式(5)和式(6),則鉆頭處的矩陣表達式為:
(7)
(8)
式中;EiIi、Pi、qi分別表示前一跨梁柱的抗彎剛度、軸向載荷和均布載荷,由于鉆頭前無梁柱,此處EiIi、Pi、qi認為是鉆頭處的抗彎剛度、軸向載荷和均布載荷;Ci1~Ci4是自變量為xi時式(5)的系數,同時也是此處矩陣表達式的未知數。
1.3.2 變截面
如圖3所示,鉆頭和螺桿的連接位置以及外徑不同的兩根鉆柱的連接位置為變截面,其連續性條件為:該處的位移、轉角、彎矩及剪力均連續;當xi=li,xj=0時,表達式為:yi=yj,θi=θj,Mi=Mj,Qi=Qj。其中li為前一跨梁柱的長度,θi為xi處對應的轉角,Qi為xi處對應的剪力,θj為xj處對應的轉角,Mj為xj處對應的彎矩,Qj為xj處對應的剪力。
將其聯立式(5)和式(6),則變截面處矩陣表達式為:
(9)
(10)
式中:EjIj、Pj、qj分別表示后一跨梁柱的抗彎剛度、軸向載荷和均布載荷;Cj1~Cj4是自變量為xj時式(5)的系數,同時也是此處矩陣表達式的未知數。
1.3.3 穩定器

將其聯立式(5)和式(6),則穩定器處矩陣表達式為:
(11)
1.3.4 管柱彎點
如圖3所示,管柱彎點處的連續性條件為:彎點處位移、彎矩、剪力都連續,但轉角由于彎角的影響發生轉角間斷[12];當xi=li,xj=0時,表達式為:yi=yj,θi-θj=θt,Mi=Mj,Qi=Qj。其中θt表示單彎螺桿管柱彎點處的彎角。
將其聯立式(5)和式(6),則管柱彎點處矩陣表達式為:
(12)
1.3.5 上切點

將其聯立式(5)和式(6),得上切點處矩陣表達式為:
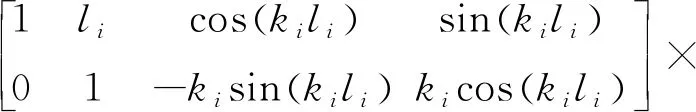
(13)
上述各節點矩陣表達式都形如AX=B,其中A為系數矩陣,X為未知數矩陣,B為增廣矩陣。
1.4 整體力學模型統一方程組的建立
根據單彎螺桿實際下部鉆具組合結構,按照節點對其跨段劃分。其中,首尾節點分別是鉆頭和上切點。利用微元法和連續梁理論,并充分考慮實際井眼軌跡、鉆具組合結構參數(穩定器直徑和位置)、彎角和鉆壓等各種因素的影響,以鉆頭至上切點的方向,依據單彎螺桿下部鉆具組合力學分析中各節點處的邊界條件、連續性條件和位移條件所建立的各節點矩陣表達式,按節點順序將每個節點對應的矩陣表達式組合在一起,形成單彎螺桿下部鉆具組合整體力學統一方程組,據此建立單彎螺桿下部鉆具組合整體力學模型。整體力學統一方程組具體表達式如下:
(14)
式中:An表示第n個節點處對應的矩陣表達式中的系數矩陣,Cn表示第n個節點處對應的矩陣表達式的未知數矩陣,Zn表示第n個節點處對應的矩陣表達式中的增廣矩陣。
實際上,A1和An分別是鉆頭和上切點處矩陣表達式中的系數矩陣,且都為2×4即兩行四列的矩陣,其余Ai(i=2~n-1)都為4×8的矩陣,在位置上,Ai的后四列與Ai+1的前四列相對應。
2 單彎螺桿鉆具組合控制井斜能力的影響因素分析
2.1 單彎單穩螺桿鉆具組合
影響單彎單穩鉆具組合控制井斜能力的主要因素包括鉆壓、螺桿彎角、肘點位置、穩點器直徑和穩定器位置等。為了分析各因素對單彎單穩鉆具組合控制井斜能力的影響規律,采用的某單彎單穩螺桿鉆具組合如下:?215.9 mm PDC+?165.0 mm螺桿(1.25°彎角,?213.0 mm穩定器)+?127.0 mm無磁加重鉆桿。其中,彎點至螺桿上接頭距離5.33 m,穩定器中點至彎點距離1.33 m,穩定器中點至螺桿鉆具下接頭端面距離0.64 m,其他計算條件包括井斜角90°,鉆壓90 kN,鉆井液密度1.89 g/cm3。
2.1.1 彎角對鉆頭側向力的影響
圖4表示不同鉆壓條件下,螺桿彎角對鉆頭側向力的影響規律。從圖4可以看出:在鉆壓一定時,隨著螺桿彎角的增大,鉆頭側向力呈線性增大;當彎角一定、鉆壓增大時,鉆頭側向力略有降低。因此,在實際鉆井過程中可以采用小的鉆壓和適當的彎角以達到控制井斜的目的。
2.1.2 穩定器外徑對鉆頭側向力的影響
圖5表示不同螺桿彎角條件下,穩定器外徑對鉆頭側向力的影響規律。從圖5可以看出,螺桿彎角的增大或穩定器外徑的增大都會使鉆頭的側向力增大,螺桿彎角的變化對鉆頭側向力的影響更加明顯。

圖5 穩定器外徑對單彎單穩螺桿鉆頭側向力的影響規律Fig.5 Effect of outside diameter of stabilizer on bit side force of single-bend and single-stabilizer PDM assembly
2.1.3 穩定器位置對鉆頭側向力的影響
圖6表示不同穩定器外徑條件下,穩定器位置對鉆頭側向力的影響規律。從圖6可以看出:穩定器位置的改變對鉆頭側向力影響較大,當穩定器距鉆頭越近時,鉆頭側向力越大;當穩定器逐漸靠近彎點時,鉆頭側向力減小且減小的趨勢趨于平緩,此時穩定器外徑對鉆頭側向力的影響也隨之減小。

圖6 穩定器位置對單彎單穩螺桿鉆頭側向力的影響規律Fig.6 Effect of stabilizer position on bit side force of single-bend and single-stabilizer PDM assembly
2.1.4 肘點位置對鉆頭側向力的影響
圖7表示不同穩定器外徑條件下,肘點(彎點)位置對鉆頭側向力的影響規律。從圖7可以看出,當穩定器外徑一定時,肘點距鉆頭越遠,鉆頭側向力越小。

圖7 肘點位置對單彎單穩螺桿鉆頭側向力的影響規律Fig.7 Effect of elbow position on bit side force of single-bend and single-stabilizer PDM assembly
2.2 單彎雙穩螺桿鉆具組合
分析各因素對單彎雙穩螺桿鉆具組合控制井斜能力的影響規律時,采用的單彎雙穩螺桿鉆具組合如下:?215.9 mm PDC+?172.0 mm螺桿(0.75°彎角,?212.0 mm穩定器)+?165.0 mm浮閥+?212.0 mm穩定器+?165.0 mm定向接頭+?165.0 mm無磁鉆鋌。其中,彎點至螺桿上接頭距離6.385 m,下穩定器中點至彎點的距離0.704 m,下穩定器中點至螺桿鉆具下接頭端面距離0.464 m,其他計算條件包括井斜角90°,鉆壓90 kN,鉆井液密度1.89 g/cm3。
2.2.1 彎角對鉆頭側向力的影響
圖8表示不同鉆壓條件下,螺桿彎角對鉆頭側向力的影響規律。從圖8可以看出:在鉆壓一定時,隨著螺桿彎角的增大,鉆頭側向力呈線性增大;鉆壓對鉆頭側向力的影響不明顯。

圖8 彎角對單彎雙穩螺桿鉆頭側向力的影響規律Fig.8 Effect of bend angle on bit side force of single-bend and double-stabilizer PDM assembly
2.2.2 肘點位置對鉆頭側向力的影響
圖9表示不同下穩定器外徑條件下,肘點位置對鉆頭側向力的影響規律。從圖9可以看出:當下穩定器外徑一定時,肘點位置的改變對鉆頭側向力的影響較大,隨著肘點遠離鉆頭,鉆頭側向力逐漸減小;僅改變下穩定器外徑時,鉆頭側向力隨著下穩定器外徑的增大而增大。

圖9 肘點位置對單彎雙穩螺桿鉆頭側向力的影響規律Fig.9 Effect of elbow position on bit side force of single-bend and double-stabilizer PDM assembly
2.2.3 兩個穩定器的間距對鉆頭側向力的影響
圖10表示不同上穩定器外徑條件下,兩個穩定器的間距對鉆頭側向力的影響規律。從圖10可以看出:上穩定器外徑一定時,隨著兩個穩定器間距的增大,鉆頭側向力先減小后增大;僅改變上穩定器外徑時,鉆頭側向力隨著上穩定器外徑的減小而增大;當兩個穩定器間距越大時,上穩定器外徑對鉆頭側向力影響越小。用該鉆具穩斜,建議兩個穩定器的距離在8 m左右。
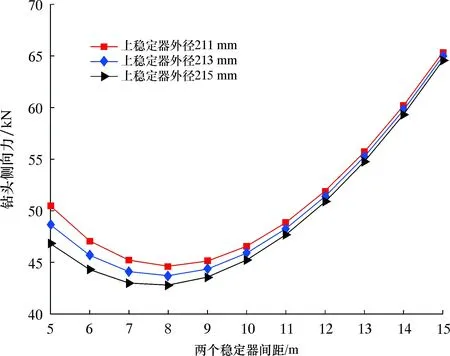
圖10 兩個穩點器間距對單彎雙穩螺桿鉆頭側向力的影響規律Fig.10 Effect of spacing between two stabilizers on bit side force of single-bend and double-stabilizer PDM assembly
3 結 論
(1)基于微元法和連續梁理論建立的單彎螺桿下部鉆具組合統一力學模型并聯合MATLAB軟件的計算方法,不僅降低了以往對于多跨梁柱的計算復雜度,還可以解決單彎螺桿下部鉆具組合中帶有多彎角和多變截面(多剛度)問題,能滿足工程實際中復雜的單彎螺桿下部鉆具組合力學模型的計算。
(2)對單彎單穩螺桿下部鉆具組合管柱進行優化設計時,適當增大螺桿彎角、減小肘點和穩定器距鉆頭的距離以及增大穩定器直徑都可以增大鉆頭側向力,提高鉆具的增斜效果。
(3)對單彎雙穩螺桿下部鉆具組合管柱進行優化設計時,為增大鉆頭側向力,提高鉆具的增斜效果,除了適當增大螺桿彎角和下穩定器直徑、減小肘點距鉆頭的距離以及減小上穩定器直徑等因素外,還可以適當增大兩個穩定器的間距。
(4)對于單彎螺桿鉆具組合而言,螺桿彎角、肘點位置、穩定器位置、穩定器外徑以及雙穩定器間距是控制井斜能力的關鍵因素,鉆壓的改變對鉆頭側向力的影響不大。

