管道柔性測徑清管器的設計及測徑盤性能分析*

張 行 劉 彤 劉思敏 許學峰 高孟琦 閆增瑞 張仕民

(1.中國石油大學(北京)機械與儲運工程學院 2.中油國際管道公司)

0 引 言

油氣管道投產前，需要對新建管道內部進行檢查評估[1-2]。在役管道也經常使用測徑清管器檢測其內部的變形情況[3-5]。目前，檢測管道內部變形情況的常用工具是管道測徑清管器。

傳統測徑清管器是在常規清管器上加裝測徑鋁盤[6],當測徑清管器運行結束后，通過檢測鋁盤變形量粗略估計管道內部發生的最大變形量。這種測徑清管器檢測精度低，不能對管道多個變形位置進行測量，并且還存在鋁制測徑盤不可重復利用的缺點。近年來，管道內部變形檢測方法主要有接觸式通徑檢測和非接觸式無損檢測[7-15]。王宇楠等[16]在泡沫清管器中放置磁塊，根據磁場變化對管內殘余物質的高度和外形等特征進行預先測量。馬書義等[17]根據回波信號的時間歷程、幅值等信息獲取管道截面的變化。趙翰學等[18]研發了150 mm大量程、高精度渦流傳感器實現對管道變形的檢測。WANG H.昊等[19]為檢測直徑小于200 mm的管道而提出鋼板彈簧卡尺探測臂。接觸式通徑檢測方法不僅存在探測臂引發機械故障的風險，而且還有檢測速度慢的缺點。非接觸式無損檢測方法檢測費用較高，設備結構復雜，再加上管道結構多樣以及服役環境等原因，應用存在局限性[20-21]。

針對上述問題，本文提出一種油氣管道柔性測徑清管器。該清管器將傳統鋁制測徑盤改為柔性材質，并將應變片置于超彈性柔性盤中,其工作原理是：當測徑清管器越過管道凹陷處時，柔性盤發生變形，應變片也隨之發生變形，應變儀測得測徑盤遇阻時的應變變化，據此可以快速識別管道內通徑變化情況，對管道變形處實現較準確的檢測和量化。這種檢測手段既可以對管內多個變形進行測量，同時又能減少引發機械故障的風險。其檢測設備在運行過程中對管壁無損傷且柔性測徑盤可重復利用。

本文以聚氨酯材質測徑盤為研究對象，采用ABAQUS 2016有限元仿真軟件對其在凹陷管道內運行情況進行模擬。從放置面、縱向分布和橫向分布3方面確定應變片放置位置，討論厚度、瓣數及聚氨酯材料硬度3個參數變化時，測徑盤應力與應變的分布，并進行分析。

1 有限元模型

1.1 柔性測徑盤模型

柔性測徑盤如圖1所示。柔性測徑盤外徑Dg為管道內徑的95%，Dg=196.64 mm；Dr表示剛體外徑，即測徑盤的內徑,Dr=51 mm；D表示每瓣之間的距離，D=10 mm；tg為測徑盤的厚度。

圖1 柔性測徑盤Fig.1 Flexible gauging plate

實際測徑盤是用 “U”形將盤分割成若干瓣，n表示測徑盤的瓣數。討論測徑盤的厚度(tg)、瓣數(n)和聚氨酯硬度等3個參數對柔性測徑盤應力和應變的影響，3個參數的變化如表1所示。

表1 不同模擬情況下測徑盤參數Table 1 Gauging plate parameters under different simulation conditions

1.2 管道及凹陷模型

凹陷大小通常由深度、長度和寬度決定[22]。本文研究的凹陷如圖1b所示。其中H是凹陷深度，Dp是管道外徑，t是管道壁厚。以?203.2 mm(8 in)管道為例，Rp=109.5 mm，t=6 mm。

對于管道凹陷基于深度的定義，許多規范都提出了評價標準[23-25]，本文中凹陷深度為15 mm。由于管道和清管器都是回轉體，所以使用極坐標系進行分析。從管道軸向看，逆時針方向是正方向，凹陷中心位于270°。

1.3 測徑盤和帶有凹陷管道的有限元模型

在ABAQUS 2016有限元軟件中，測徑盤在凹陷管道運行時的有限元模型如圖2所示。為保證網格質量，測徑盤選擇六面體單元網格，在與管道凹陷接觸的測徑盤邊緣進行倒角處理并加密網格，共有68 248個網格單元。管道同樣選擇六面體單元，共有10 318個網格單元。在管道凹陷處，選擇四面體進行網格劃分，共有5 115個網格單元。

圖2 測徑盤有限元模型Fig.2 Finite element model of gauging plate

管道的彈性模量是2.01 MPa，泊松比是0.3。測徑盤采用聚氨酯材料，以Mooney-Rivlin為本構模型[26]，其邵氏硬度與材料特性常數C01、C10的關系如表2所示。考慮管道無軸向位移，管道外壁及凹陷處受完全約束。為提高運算速率，將管道凹陷處簡化為剛體。

表2 聚氨酯材料參數Table 2 Polyurethane material parameters

2 測徑盤過管道凹陷運行分析

2.1 測徑盤過管道凹陷過程的應力分析

第10組算例用于分析測徑盤過管道凹陷過程中應力與應變的變化情況。測徑盤在凹陷管道運行過程如圖3所示。4個典型位置對應的測徑盤應力云圖如圖4所示。以測徑盤與凹陷接觸的面為正面，反之為背面。

圖3 模擬過程及結果Fig.3 Simulation process and results

測徑盤接觸凹陷前無應力變化。當測徑盤繼續向前運行，底瓣接觸管道凹陷并緊貼凹陷輪廓向上“抬起”，應力隨之增大，到達凹陷最高處時，測徑盤底瓣徑向上升到最大高度，測徑盤應力達到最大。然后，測徑盤底瓣沿管道凹陷輪廓慢慢“落下”，應力隨之減小，越過凹陷后測徑盤恢復原狀，底瓣所受應力也恢復至0。

由圖4可知，測徑盤遇凹陷過程中，離測徑盤孔徑近的位置應力更大，其應力沿圓盤半徑至邊緣方向以“水波紋”的形式逐級遞減。在測徑盤底瓣“頸部”邊緣會出現應力集中，若將應變片放置在此處，則測徑盤經過微小凹陷時也會產生較大應力，這不能反映管道內部真實狀況。考慮到實際操作，在邊緣處不便加裝應變片，所以在后續分析應變片優選位置時，此處不做考慮。

圖4 4個典型位置的應力云圖Fig.4 Cloud chart of stress at 4 typical positions

2.2 確定應變片放置面

在測徑盤遇凹陷過程中，其正面受到拉應力，背面受到壓應力。放置應變片時，應以應變變化更大的一面，即應變率更高的面為優選。從測徑盤底瓣外緣沿半徑方向的中心線上等距選取10 個節點，如圖5所示。以Point2為例，比較正、背面的應變率，其結果如圖6所示，正面的應變變化比背面更明顯，以此可知應在測徑盤正面放置應變片。

圖5 測徑盤正面節點取情況Fig.5 Selection of front nodes and lines of gauging plate

圖6 Point2正、背面應變和應變率隨時間變化曲線Fig.6 Variation curve of front and back strain and strain rate with time at Point 2

2.3 確定應變片縱向位置

沿圓盤半徑方向做7條線將底瓣等分，每條線的起點都為測徑盤孔徑邊緣，等距選取10個節點，如圖7所示。測徑盤每條線上不同點的應變-位移曲線如圖8所示。首先分析第4條線上10個點的應變情況。由圖8a可知，Point1～Point3在10個點中應變變化顯著，其中Point2在測徑盤底端到達管道凹陷最高處時,應變達到最大。選取Point1、Point3、Point5、Point7、Point9進行應變比較。從圖8b～8h可以看出：由于Point3接近應力集中點，所以其應變變化非常明顯；圖8c～圖8g中Point1與Point3這兩點之間應變相差微小，后幾點之間應變差距較大。由此可得，應變片縱向位置介于Point1～Point3之間最合適。

圖7 測徑盤正面7條線Fig.7 7 lines on the front of the gauging plate

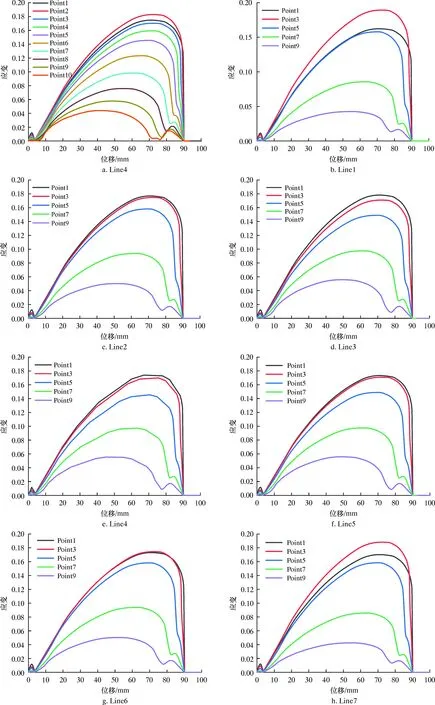
圖8 測徑盤每條線上不同點的應變-位移曲線Fig.8 Strain-displacement curve of different points on each line of the gauging plate

2.4 確定應變片橫向位置

Line1～Line7的前3個節點應變-位移曲線如圖9所示。

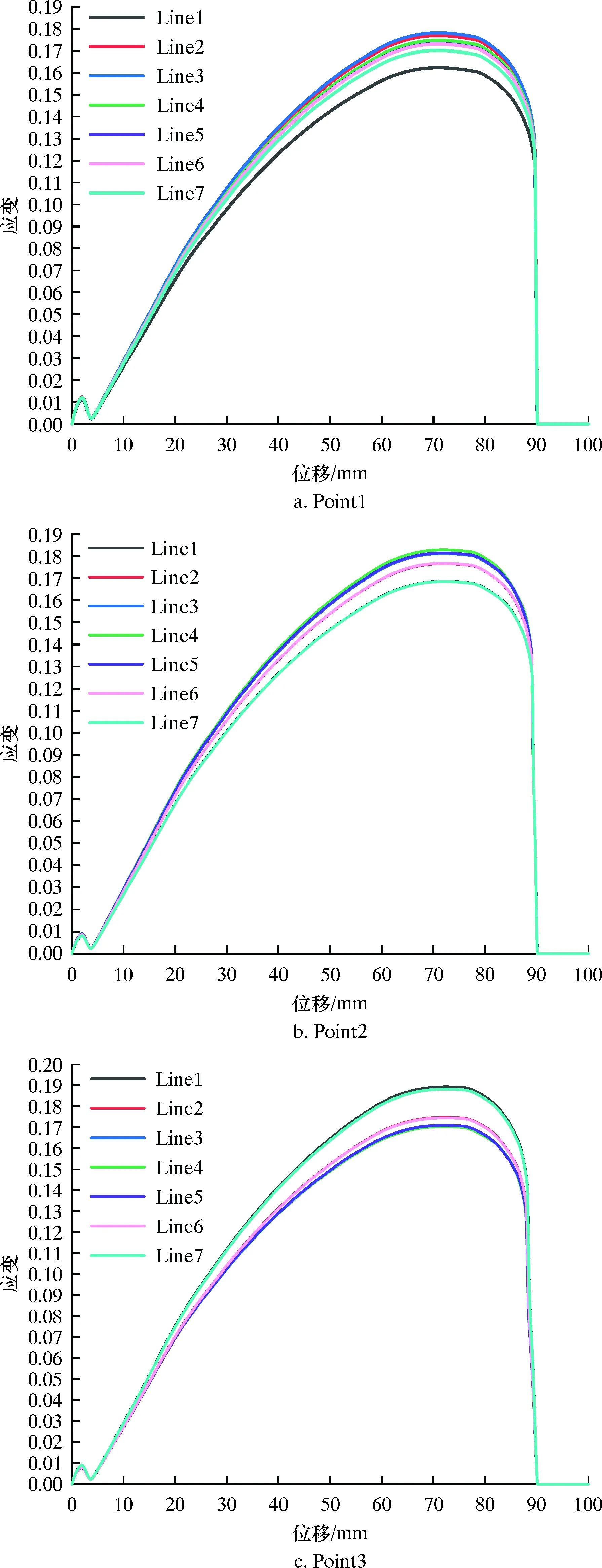
圖9 不同線上的前3節點應變-位移曲線Fig.9 Strain-displacement curve of the first three nodes on different lines

由圖9可知：第3條線上第1節點的應變隨位移變化最明顯，第1條線變化最弱；第1條和第7條線的應變曲線幾乎重合且變化最不明顯；由于第1和第7條線的第3節點距離測徑盤應力集中點較近，所以不能合理有效地提供應變數據。由此可得，應變片的橫向位置應處在Line2～Line6之間。綜上所述，應變片放置在測徑盤正面每瓣根部中心位置，有利于提升檢測系統的靈敏度。

2.5 網格獨立性

將算例10用于網格獨立性分析。當單元尺寸分別為1.1和1.5 mm時，計算得測徑盤底瓣位于C點時的應力分別為2.301和2.299 MPa，二者相差0.09%，這兩種網格具有良好一致性。因此，構建的網格具有獨立性。

3 不同參數對測徑盤過凹陷的應力與應變影響

由前文可以得出，Line4 的第2節點應變變化最顯著，將此點記為M，M點是對不同參數研究最具代表性的一點。

3.1 厚度對測徑清管器測徑盤M點應力和應變的影響

設n=8，聚氨酯材料硬度為70 HS時，測徑盤厚度tg=12、15、18和21 mm，其他條件不變。圖10為不同厚度下測徑盤的應力與應變分布。由圖10可知，M點在測徑盤底瓣底端位于凹陷最高點處的應力應變分布，相應的應變云圖如圖11所示。從圖10可得，厚度從12 mm增加到21 mm，M點應力從0.67 MPa增加到1.42 MPa，其應變變化也有相似趨勢。除M點外，測徑盤其他位置的應力應變也隨著測徑盤厚度的增加而增加。

圖10 不同厚度下測徑盤的應力與應變分布Fig.10 Stress-strain distribution of gauging plate with different thickness

圖11 不同厚度測徑盤的應變云圖Fig.11 Cloud chart of strain of different thickness of gauging plate

3.2 瓣數對測徑盤M點應力和應變的影響

當tg=20 mm、聚氨酯材料硬度為70 HS時，測徑盤瓣數從6瓣變為7、8和9瓣，其他條件不變。圖12為M點在測徑盤底瓣底端位于凹陷最高點處的應力與應變分布，相應的應變云圖如圖13所示。從圖12可知，隨著瓣數的增加，應力和應變變化并不顯著。

圖12 不同瓣數下測徑盤的應力與應變分布Fig.12 Stress-strain distribution of gauging plate with different flap numbers

圖13 不同瓣數下測徑盤的應變云圖Fig.13 Cloud chart of strain of gauging plate with different flap numbers

3.3 聚氨酯材料硬度對測徑盤M點應力和應變的影響

當tg=20 mm、n=8時，測徑盤材料硬度從60 HS依次變為65、70和75 HS，其他條件不變。圖14為M點在測徑盤底瓣底端位于凹陷最高點時的應力與應變分布，相應的應變云圖如圖15所示。

圖14 不同聚氨酯材料硬度下測徑盤的應力與應變分布Fig.14 Stress-strain distribution of gauging plate with different hardness

圖15 不同聚氨酯材料硬度測徑盤的應變云圖Fig.15 Cloud chart of strain of gauging plate with different polyurethane hardness

從圖14可知,M點的應力隨聚氨酯材料硬度的增加而增加，但應變沒有實質性的變化。這是由于隨聚氨酯材料硬度的增加，測徑盤變得不易彎曲，所以應變變化很小。

4 結 論

(1)柔性測徑清管器既可實現對管內多個變形進行準確檢測，其柔性測徑盤又可重復利用，同時可以提升檢測作業的安全性，其成本低、適用范圍廣的特點可滿足不同的作業環境要求。

(2)在柔性測徑盤越過凹陷過程中，其變形瓣的應力沿半徑方向呈“水波紋”形式逐級遞減分布，在變形瓣“頸部”邊緣會出現應力集中現象。

(3)應變片放置在測徑盤正面每瓣根部中心位置時應變變化更顯著，有利于提升檢測系統的靈敏度。

(4)測徑盤的厚度比瓣數和材料硬度對其應力與應變的影響大，瓣數對應力和應變的影響最小。