宜昌城區短歷時暴雨強度公式參數優化及暴雨雨型特征分析

張鵬宇 王振洋 張雅 曾令

摘要：基于歷史降雨資料，采用數理分析方法，獲得城市暴雨特征的量化表達，是城市風險管控、基礎設施規劃設計的關鍵性基礎工作之一。根據宜昌城區短歷時暴雨觀測資料，應用遺傳算法分別對皮爾遜-Ⅲ型頻率分布曲線和暴雨強度公式參數進行了優化求解，通過趨勢分析得到了近30 a的年際變化特征，采用芝加哥法分析確定了短歷時暴雨雨型。結果表明：確定的宜昌城區暴雨強度滿足精度要求;宜昌城區近30 a短歷時暴雨的雨量峰值趨于增加，暴雨發生的歷時主要集中在3 h以內。采用芝加哥法確定了重現期為2 a各降雨歷時（步長取5 min）的設計暴雨雨型，雨峰位置的降雨強度隨降雨歷時的增加呈現出一定的上下波動，但各歷時峰值在數值上相差并不明顯。研究成果可為城市雨水徑流控制等提供參考。

關鍵詞：暴雨強度;雨型特征;參數優化;趨勢分析;宜昌城區

中圖法分類號：TV122.1文獻標志碼：ADOI：10.15974/j.cnki.slsdkb.2021.06.001

文章編號：1006 - 0081（2021）06 - 0008 - 04

1 研究背景

近年來，隨著全球氣候變化，極端暴雨事件越來越頻繁[1]，成為社會各界關注的焦點。宜昌市地處鄂西南丘陵山地，典型地形氣候特征的暴雨時有發生。此外，近年來城市發展對區域水文循環產生的影響不容忽視，暴雨致澇問題日漸突出。城市暴雨內澇與強降雨密切相關，而短歷時的強降雨是引起城市內澇的主要原因之一[2]。因此，研究宜昌城區短歷時降雨強度、降雨歷程等規律、特征及其變化情況，對于城市風險管控、基礎設施建設都具有重要意義。

暴雨強度公式是基于歷史降雨實測資料，采用數理分析方法獲得的描述城市暴雨特征的定量表達，是城市排水系統等基礎設施規劃與設計的基礎[3]。頻率分布函數和強度公式參數優化是確定暴雨強度公式的重要環節，參數取值準確與否決定暴雨強度公式計算成果的參考價值。然而，上述模型均具有非線性的特點，《城市暴雨強度公式編制和設計暴雨雨型確定技術導則》[4]（下稱“導則”）指出，基于歷史降雨數據，通過數學優化計算是確定以上參數的有效途徑。在我國應用最廣泛的皮爾遜-Ⅲ型頻率分布函數參數優化方面，矩法、權函數法、適線法等[5]最為常見。其中，矩法計算簡單，但求解精度偏低，特別是當樣本容量較小時，采用該方法獲得的參數常常存在較大的偏差;基于權函數的優化方法本質與矩法相同，普通權函數法僅針對單參數優化問題，難以對皮爾遜-Ⅲ型頻率曲線的多個參數進行聯合優化，而雙權函數法雖然在一定程度上提升了求解精度，但仍未從根本上解決精度不足的問題;適線法的求解精度對操作者的主觀意志較為敏感，難以擺脫主觀隨意性的影響。在暴雨強度公式參數優化方面，最常見的方法是最小二乘法、高斯牛頓法[6]，采用以上方法在優化過程中難以跳出局部最優解。近年來，隨著計算機技術和仿生群智能優化算法的持續發展與進步，遺傳算法[7-8]、人工蜂群算法[9]等方法被逐漸應用于暴雨強度公式參數確定中，效果較好。

為此，本文基于宜昌城區氣象資料，采用遺傳算法對皮爾遜-Ⅲ型頻率分布函數和強度公式參數進行優化求解，推導出符合精度要求的暴雨強度公式，并對公式的計算精度進行驗證。最后，對宜昌城區短歷時暴雨雨型特征進行分析，研究成果以期為城市基礎設施規劃與設計提供參考。

2 基礎資料與分析方法

采用長江水利委員會水文局三峽水文水資源勘測局宜昌蒸發站資料作為本文分析的基礎資料，采用該站1990～2019年共計30 a暴雨自記雨量資料，根據年最大值法選取了每年10，30，60，180，360 min共5個歷時的最大降雨值為暴雨強度公式編制樣本。采用遺傳算法分別對皮爾遜-Ⅲ型頻率分布函數和暴雨強度公式參數進行優化求解，得到宜昌城區暴雨強度公式，在此基礎上，采用芝加哥法[10]推求設計暴雨雨型，并對其特征進行分析。

2.1 皮爾遜-Ⅲ型頻率分布曲線參數優化原理

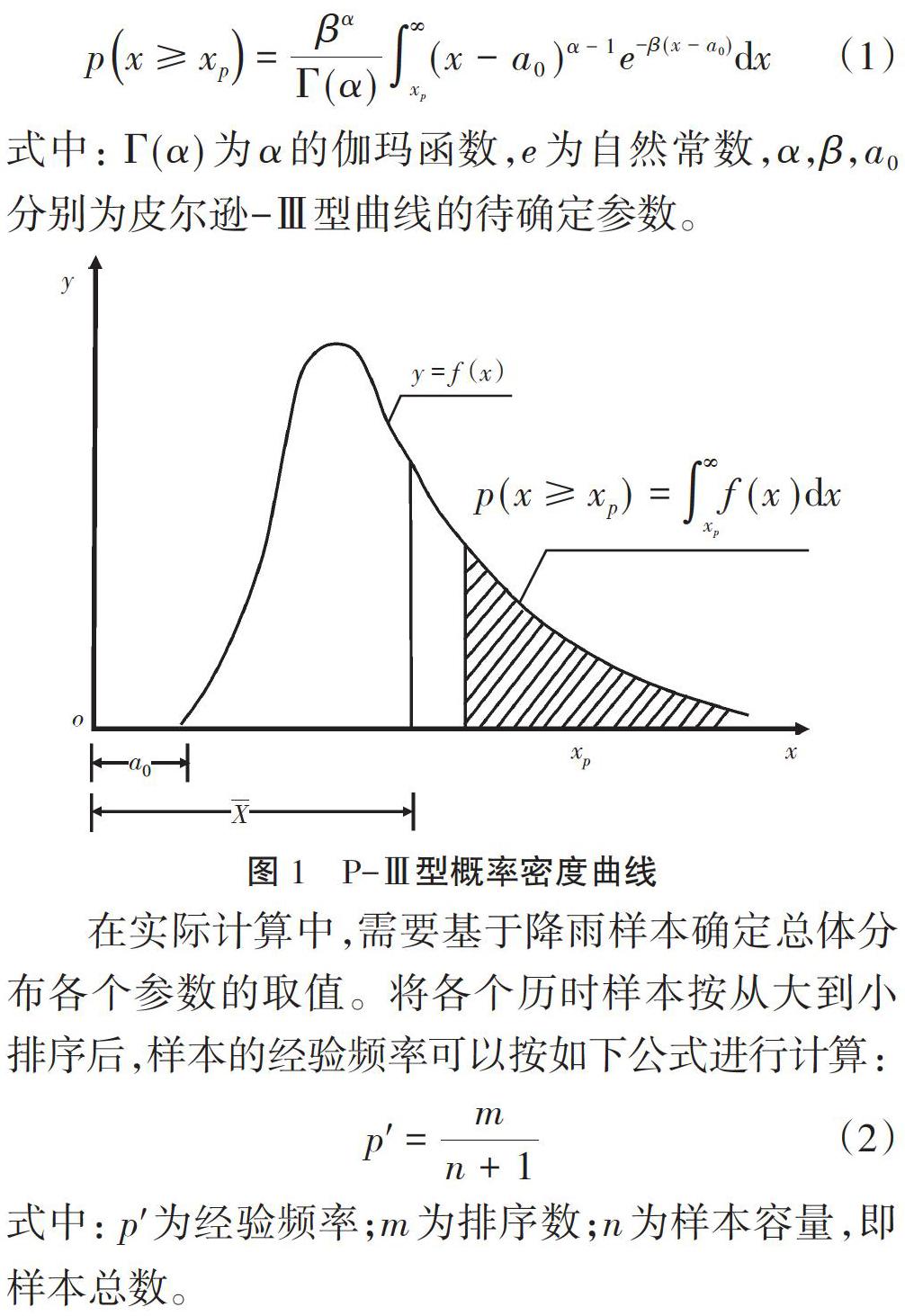
皮爾遜-Ⅲ型概率密度函數曲線如圖1所示。降雨頻率分析中需要對皮爾遜-Ⅲ型分布的概率密度函數進行積分：

在實際計算中，需要基于降雨樣本確定總體分布各個參數的取值。將各個歷時樣本按從大到小排序后，樣本的經驗頻率可以按如下公式進行計算：

確定經驗頻率后，通過一定策略不斷調整皮爾遜-Ⅲ型分布函數中[α]，[β]，[a0]待確定的參數值，直至理論計算頻率與經驗頻率之間的誤差盡可能小時，對應的[α]，[β]，[a0]即為所求的參數值。由此，將參數估計問題轉化成為非線性規劃問題，可以建立如下優化目標函數：

得到頻率分布函數后，即可獲得當地重現期（[P]）、降雨強度（[i]）和降雨歷時（[t]）之間的關系。

2.2 暴雨強度公式參數優化原理

暴雨強度公式描述了當地[P]-[i]-[t]之間的定量關系。由于不同地區的降雨存在不同程度的差別，因此，暴雨公式需要通過當地的降雨資料分析確定。根據導則，暴雨強度公式如下：

將暴雨強度公式參數估計問題轉化成非線性規劃問題，根據當地[P]-[i]-[t]之間的關系，以暴雨計算強度計算值[ik]與經驗計算值[i′k]之間的絕對均方差建立目標函數：

式中： [ik]為第[k]項觀測值的理論計算暴雨強度;[i′k]為第[k]項觀測值的經驗暴雨強度;[F]為暴雨強度理論計算值與經驗值的誤差平方和。

為確保暴雨計算值的可靠性，需要對獲得的暴雨強度公式進行精度校驗。根據導則規定，在一般降雨強度區域，當計算重現期為2～20 a時，暴雨強度計算值與經驗值的平均絕對均方差宜控制在0.05 mm/min以內，平均相對均方差不宜超過5%。

式中： [X]為平均絕對均方根誤差;[U]為平均相對均方根誤差。

2.3 遺傳算法原理

遺傳算法[7-8]是一類仿自然界進化規律的隨機搜索算法，在處理非線性模型參數優化的問題中表現出較強的通用性和可靠性。其基本思想是從一組隨機初值產生的初始種群為起點，采用隨機化的策略對在一個參數區間內實現高效尋優計算，從而獲得問題的近似解，并以近似解的適應度來衡量解的優劣，然后，基于過程解的優劣程度，對種群進行選擇、交叉和變異操作實現算法的遺傳特性，使得近似解的質量演變朝著最優的方向進行，如此經歷多次迭代計算，輸出問題的最優解。

3 結果分析

3.1 皮爾遜-III型曲線參數優化結果

根據長江三峽水文水資源勘測局宜昌蒸發站1990～2019年（30 a）5個歷時（10，30，60，180，360 min）暴雨雨量資料，按從大到小排序，得到各個歷時30個暴雨樣本數據。以式（3）為目標函數，采用遺傳算法對各個歷時的皮爾遜-III型分布曲線參數進行優化，優化結果如表1所示，相應的頻率分布曲線如圖2所示，可以看出，優化結果和經驗頻率擬合較好，說明獲得的參數具有較高的可靠性。

3.2 暴雨強度公式參數優化結果

基于優化后的皮爾遜-III型概率分布曲線，得到宜昌城區降雨[P]-[i]-[t]之間的關系，以式（5）為目標函數，采用遺傳算法對暴雨強度公式的參數進行優化，最終獲得宜昌城區暴雨強度公式：

按照式（8）求得在重現期為2～20 a時的平均絕對均方根誤差為0.042 [mm/min]，小于0.05[ mm/min]，平均相對均方根誤差為3.16%，低于5%;以上均滿足精度要求。

3.3 短歷時暴雨特征分析

3.3.1 年際變化特征

從宜昌城區逐年雨量資料中選擇1990～2019年歷時為10，30，60，180 min和360 min的年最大降雨量值進行統計分析，各個歷時年最大降雨量的變化趨勢見圖3～4。近30 a宜昌城區各歷時最大降雨量波動較大，其中，10，180 min和360 min年最大降雨量分別以2.52，2.99，3.10 mm/10 a增加，增加趨勢較為顯著;30 min和60 min年最大降雨量變化趨勢無確定性規律，僅表現為周期性波動;總體而言，近30 a宜昌城區短歷時暴雨的雨量峰值趨于增加。圖4結果顯示，180 min和360 min年最大降雨量序列吻合程度較高，說明近30 a宜昌城區短歷時暴雨發生的歷時主要在3 h以內。

3.3.2 設計雨型特征分析

基于前文獲得的宜昌城區暴雨強度公式，采用芝加哥法分析確定其短歷時暴雨雨型。根據現有研究，宜昌城區綜合雨峰位置系數r取0.28[11]。計算步長設定為5 min，計算得到重現期為2 a時各降雨歷時的峰值、雨峰時段匯總如表2所示，以及短歷時降雨強度及累計降雨量，如圖5～6所示。由表2可知，宜昌城區短歷時暴雨的設計雨型為單峰型，隨著降雨歷時的增加，雨峰時刻對應的降雨強度呈現出上下波動變化。其中，降雨歷時為30，60 min和90 min的峰值分別發生在第2、第4和第6時段，位于整個降雨歷程的1/3分位;降雨歷時120，150 min和180 min的峰值分別發生在第7、第9和第11時段，位置略超前于整個降雨歷程的1/3分位。雨峰處降雨強度雖表現出一定的波動，從圖5來看，不同歷時峰值差異相對較小。由圖6可知，重現期為2 a時，歷時為30 min的降雨累積雨量呈現出“劇烈-平緩”的增長趨勢，而歷時為60～180 min的降雨累積雨量呈現出“平緩-劇烈-平緩”的增長趨勢，且首段平緩發展時間隨降雨歷時增長而延長。

4 結 論

（1）遺傳算法用于宜昌城區皮爾遜-Ⅲ型頻率分布曲線和暴雨強度公式參數優化，實現了以上模型多個參數的聯合識別，得到了宜昌城區暴雨強度公式。誤差分析結果表明，本文確定的宜昌城區暴雨強度公式滿足精度要求，同時表明遺傳算法對于各類非線性模型參數的優化具有較強的適用性。

（2）宜昌城區近30 a短歷時暴雨的雨量峰值趨于增加，暴雨發生的歷時主要集中在3 h以內。

（3）基于宜昌城區暴雨強度公式，采用芝加哥法確定了重現期為2 a各降雨歷時（步長取5 min）的設計暴雨雨型。結果表明：雨峰位置的降雨強度隨降雨歷時的增加呈現出一定的上下波動，但各歷時峰值在數值上相差并不明顯。重現期為2 a時，歷時為30 min的降雨累積雨量呈現出“較快-緩慢”的增長趨勢，而歷時為60～180 min的降雨累積雨量呈現出“緩慢-較快-緩慢” 的增長趨勢，且首段平緩發展時間隨降雨歷時增加而加長。

參考文獻：

[1] 馬京津， 李書嚴， 王冀. 北京市強降雨分區及重現期研究[J]. 氣象， 2012，38（5）：569-576.

[2] 劉立軍， 程玉祥， 吳益. 浙江省城市暴雨計算方法的比較研究[J]. 人民黃河， 2013，35（5）：30-32， 35.

[3] 任雨， 李明財， 郭軍， 等. 天津地區設計暴雨強度的推算與適用[J]. 應用氣象學報， 2012，23（3）：364-368.

[4] 住房和城鄉建設部， 中國氣象局. 城市暴雨強度公式編制和設計暴雨雨型確定技術導則[S]. 2014.

[5] 劉俊， 周宏， 魯春輝， 等. 城市暴雨強度公式研究進展與述評[J]. 水科學進展， 2018，29（6）：898-910.

[6] 周紹毅， 羅紅磊， 蘇志， 等. 南寧市新一代暴雨強度公式與暴雨雨型研究[J]. 氣象研究與應用， 2017，38（2）：1-5.

[7] 林林， 樊建軍， 楊貴春， 等. 遺傳算法在暴雨強度公式優化問題中的應用及Matlab實現[J]. 水利與建筑工程學報， 2008（4）：30-32.

[8] 毛明策， 吳素良， 范婧兒. 基于遺傳算法的暴雨強度公式參數計算[J]. 陜西氣象， 2020（4）：50-52.

[9] 楊一葉， 王志剛， 夏慧明. 人工蜂群算法在暴雨強度公式參數優化中的應用[J]. 價值工程， 2013，32（23）：261-262.

[10] 戴有學， 王振華， 戴臨棟， 等. 芝加哥雨型法在短歷時暴雨雨型設計中的應用[J]. 干旱氣象， 2017，35（6）：1061-1069.

[11] 成丹， 陳正洪， 方怡. 宜昌市區短歷時暴雨雨型特征[J]. 暴雨災害， 2015，34（3）：249-253.

（編輯：李 晗）