分裂導線短路時動態張力計算的對比研究

程壯 陳功

摘要：為研究國內外對于分裂導線短路時動態張力計算的差異，分別基于《電氣一次手冊》和IEC 60865標準，計算了分裂導線短路時的動態張力。對比了這兩種方法之間輸入條件和計算結果的差異，最終提出了關于影響分裂導線短路時動態張力計算的若干結論：IEC算法考慮了短路動態效應和導體受力的運動過程，引入了結構掛點常數，更接近實際情況，一次手冊算法計算出的結果偏保守;兩種算法的計算結果差異較大，但所得出動態張力與次檔距關系的變化趨勢是一致的。論文研究結果可供工程設計人員參考。

關鍵詞：分裂導線;短路;次檔距;動態張力;臨界接觸

中圖法分類號：TM75文獻標志碼：ADOI：10.15974/j.cnki.slsdkb.2021.06.012

文章編號：1006 - 0081（2021）06 - 0059 - 04

在超高壓配電裝置中，為滿足載流量以及電暈、無線電干擾的要求，一般采用分裂導線作為設備連接線以及高跨線。在短路情況下，分裂導線所受到的短路電動力存在特殊性。在發生短路的瞬間，在同相的子導線間，由于電流的方向相同，會產生相互吸引的電磁力，并造成導線形變和偏移;同時由于子導線之間存在間隔棒，導線形變和偏移將會對末端掛點處產生一個沿導線方向的動態張力。

動態張力大小與短路電流、分裂間距、次檔距、初始靜態張力以及導線型號參數等多個因數相關。這個張力具有沖擊性質，作用時間非常短，且與導線掛點處構架剛度有關。國際上計算該動態張力的方法屬于短路動荷載計算[1-3]，且原理和步驟基本相同。國內的設計手冊里給出了一項理論計算方法[4]，并提供了算例。

國內外計算分裂導線短路時動態張力的這兩種方法，文中分別簡稱為IEC算法和一次手冊算法，二者計算公式、結果差異較大，需要對此進行進一步探討和研究。

1 計算輸入條件

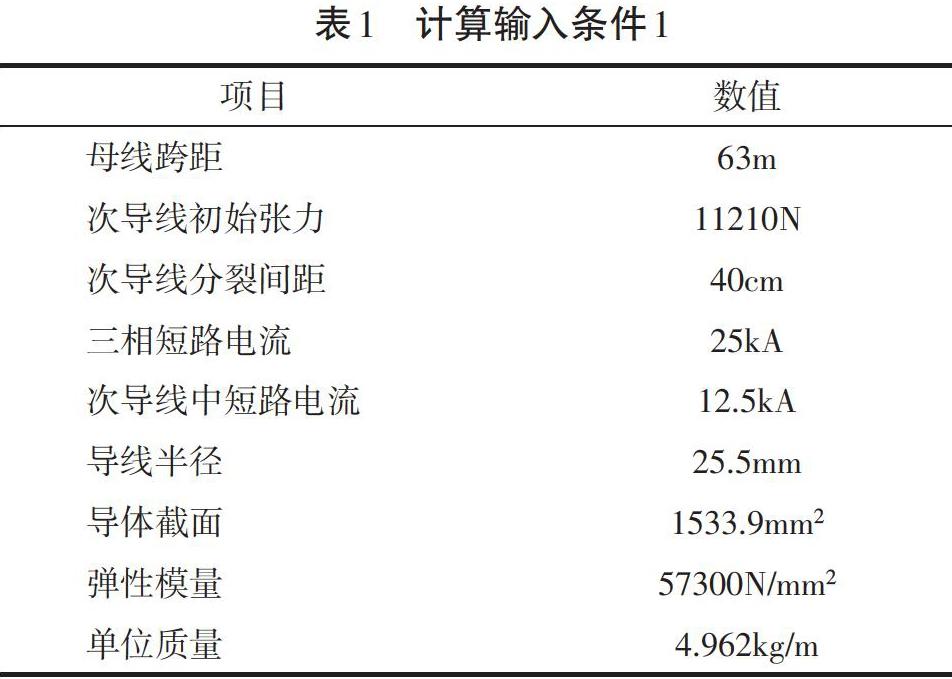
為便于對比分析，根據一次手冊上算例的輸入條件（表1），通過兩種方法的計算[4]，對計算過程、計算結果和影響因素進行比較和分析。

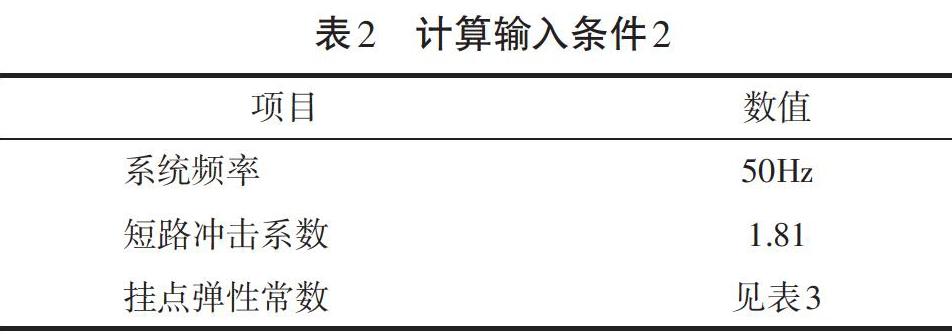
表1中提供的計算條件可用于一次手冊算法的計算;但是對于IEC算法，還需另行補充輸入條件（表2）。

其中，掛點彈性常數S表示導線掛點處結構的剛度，反映了材料或結構在受力時抵抗彈性變形的能力。其值越大，剛度越高，表現為受力條件下越難以變形。

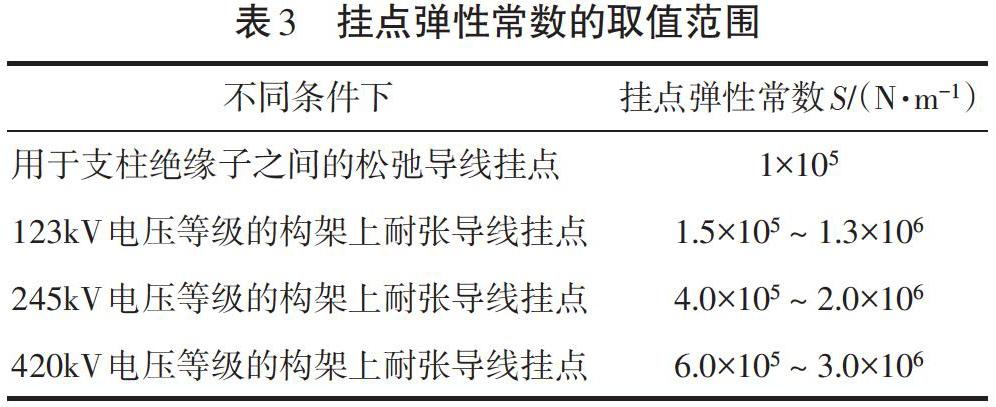
IEC標準給出了建議的取值范圍（表3）。

為分析不同S值對動態張力的影響，分別假定3個S值：1×105，6.0×105? N/m和3.0×106 N/m，并對結果進行比較。

2 計算方法

2.1 一次手冊算法

一次手冊通過假定分裂導線子導線間的相關位置關系，分為不接觸、臨界接觸、接觸3種情況，分別采用“試湊法”計算[4]。

式中：[Fm]為子導線間電動力，N;[F′m]為子導線間電磁引力，N;[T]為導體短路后每根次導線的實際張力，N;[T0]為導體的初始張力，N;[d]為次導線分裂間距，cm;[b]為兩次導線最接近點距離，cm;[E]為彈性模量，N/mm2;[S]為導體截面積，mm2;[ε]為該次檔距內導線在電磁吸力作用下的伸長率;[I]為次導線中短路電流，kA;[l0]為次檔距，cm。

（1）如圖1（a）所示子導線臨界接觸，令[Fm=F′m]，計算出臨界接觸次檔距，同時算出動態張力。

（2）如圖1（b）所示，子導線不接觸，次檔距小于臨界接觸次檔距，假定子導線間的最小距離值[b]，令[Fm=F′m]，算出動態張力。

（3）如圖1（c）所示，子導線部分接觸，次檔距大于臨界接觸次檔距，假定子導線間的接觸長度[l1]，令[Fm=F′m]，算出動態張力。

以上計算步驟可利用Excel軟件編制單變量求解的宏運算，通過改變可變項的值使得目標項的值趨于零，從而方便快捷的得出計算結果。

2.2 IEC算法

IEC算法的計算方法和公式比較復雜，且從屬于整個短路電流動態作用全過程計算中，涉及的符號較多。其計算過程步驟如下。

（1）首先判斷是否需要計算該項動態張力。對于不超過四分裂的常規分裂導體，當分裂間距[as]、子導線直徑[d]和次檔距[ls]滿足一定條件時，其短路時的“夾緊”效應不明顯，可以直接取主導線短路作用力（搖擺作用力）的1.1倍。

而當滿足[as/d≤2.0]且[ls≥50as]，或者[as/d≤2.5]且[ls≥70as]這兩個條件其一時，動態張力的作用被認為較為明顯，需要單獨計算。

（2）計算子導線間的短路作用力。

Vs/（Am）;[I″k]為短路電流，kA;[v2]，[v3]為中間值，可以用其他因數表示，公式略。

（3）引入[j]值的概念，通過比較[j]值與1的大小，來判斷子導線是否接觸。當[j]不小于1時，子導線相互接觸;當[j]小于1時，子導線未接觸。

式（7）中[N]表示柔性導線及所連接的兩側懸點所組成的一個整體系統的柔性指標，提出了“支柱絕緣子-導線”系統和“門構住-絕緣子串-導線”系統這兩種狀態下的表達公式[2]。

（4）計算不同狀態下的動態張力值。

當子導線接觸時，動態張力：

當子導線不接觸時，動態張力：

式中：[ve]公式較繁雜，[ξ]是隨[j]和[εst]變化的函數，[η]是隨[as/d]變化的函數，IEC標準內均給出了以上函數的圖表以及擬合公式[1]。

IEC算法的計算步驟，相較一次手冊算法而言，其計算公式更為繁瑣，且同樣也需要采用“試湊法”，基于Excel軟件編制計算公式并采用單變量求解運算，同樣可以便捷地解決求解問題。

3 對比分析

通過上述兩種計算方法，而且采用IEC算法時取3種掛點彈性常數值，分別獨立計算求解，計算結果見表4。

當次檔距的取值范圍從2～40 m間變化時，分別求出不同的動態張力值，并將計算結果匯總成表，生成曲線見圖2。

通過該案例，采用IEC算法和一次手冊算法分別計算，對計算方法和結果進行分析，可以得出如下判斷。

（1）兩種算法計算方法差異較大。IEC算法考慮了短路動態效應和導體受力的運動過程，并且引入了結構掛點彈性常數，更接近實際情況;掛點彈性常數取值越大，計算得出的動態張力值越大。一次手冊算法沒有考慮短路動態效應和導體受力運動，僅簡化為導體受力形變后靜態平衡，且沒有考慮結構掛點彈性系數，即假定掛點是不可形變的理想剛體，從而忽略了結構撓度對短路動態張力的削弱作用，其計算所得出的結果偏保守。

（2）兩種算法的計算結果差異較大，但所得出動態張力與次檔距關系的變化趨勢是一致的：即對于分裂導線子導線，由不接觸到臨界接觸狀態，再到接觸面擴大，其動態張力是先變大后變小，靠近臨界接觸狀態時動態張力值最大。

（3）從工程實踐角度出發，掛點處的彈性常數值，實際上與結構設計密切相關。結構設計規范一般僅規定不同構支架的允許撓度值，而對于高度不同、靜態受力不同、以及結構材質不同的構支架或設備掛點，其彈性常數均不盡相同，且不易得出準確值，工程中可以參考IEC標準給出的推薦范圍值選取。

（4）在短路電流、導線參數及總跨度等其他條件一定的情況下，次檔距是影響分裂導線短路時動態張力的重要因素，因此合理選擇次檔距，是減小結構受到導體短路沖擊力的重要手段。

（5）分裂導線次檔距的選擇，需盡量避開臨界接觸點，使得子導線處于非接觸區或者接觸區，以降低導線對掛點處結構的荷載;且圖2中非接觸區斜率較接觸區更大，即非接觸狀態下次的檔距減小對動態張力影響更大。因此，對于發變電工程，可以采用間隔棒密布以減小次檔距方式，也可以采用減少間隔棒以增大次檔距的方式。對于設備之間的連接線，由于距離一般較短，宜采用間隔棒密布的方式。

4 結 語

本文通過對某一具體案例，分別基于電氣一次手冊和IEC標準，計算了分裂導線短路時的動態張力，并且對兩種計算的方法和結果對比和分析，得出影響分裂導線短路時動態張力的結論。

通過計算對比分析，可增強設計人員對分裂導線短路情況下動態過程的理解，幫助解決變電工程分裂導線設計的實際問題。

隨著我國“一帶一路”倡議的實施，涉外發、變電工程日益增多。采用國際規范進行工程設計，是國內工程設計人員所面臨的主要難點之一。通過深入比較國內外計算方法上的差異，有助于提高設計能力和設計水平。

參考文獻：

[1] IEC 60865-1-2011 Short-circuit currents. Calculation of effects. Part 1 Definitions and calculation methods[S].

[2] IEEE Std 605-2008 Bus Design in Air Insulated Substations[S].

[3] CIGRE Technical Brochure 105 The mechanical effects of short circuit currents in open air substations （Rigid and flexible bus bars）[S].

[4] 水電力部西北電力設計院編.電力工程電氣設計手冊 電氣一次部分[M]. 北京：中國電力出版社，1989：379-383.

（編輯：唐湘茜）