量子態制備及其在量子機器學習中的前景*

趙健 陳昭昀 莊希寧3) 薛程 吳玉椿2)? 郭國平2)3)

1) (中國科學技術大學, 中國科學院量子信息重點實驗室, 合肥 230026)

2) (合肥綜合性國家科學中心人工智能研究院, 合肥 230088)

3) (合肥本源量子計算科技有限責任公司, 合肥 230026)

經典計算機的運算能力依賴于芯片單位面積上晶體管的數量, 其發展符合摩爾定律. 未來隨著晶體管的間距接近工藝制造的物理極限, 經典計算機的運算能力將面臨發展瓶頸. 另一方面, 機器學習的發展對計算機的運算能力的需求卻快速增長, 計算機的運算能力和需求之間的矛盾日益突出. 量子計算作為一種新的計算模式, 比起經典計算, 在一些特定算法上有著指數加速的能力, 有望給機器學習提供足夠的計算能力. 用量子計算來處理機器學習任務時, 首要的一個基本問題就是如何將經典數據有效地在量子體系中表示出來. 這個問題稱為態制備問題. 本文回顧態制備的相關工作, 介紹目前提出的多種態制備方案, 描述這些方案的實現過程, 總結并分析了這些方案的復雜度. 最后對態制備這個方向的研究工作做了一些展望.

1 引 言

機器學習是一門人工智能領域的科學, 其通過計算機學習訓練已知的數據, 并利用訓練好的數據模式預測未知數據的信息. 隨著計算機性能的不斷增強, 機器學習對數據的處理能力也不斷提升, 被廣泛應用到各個領域[1]. 這包括圖像識別[2,3]、人臉識別[4-6]等分類問題, 也包括最優決策問題, 如Alpha Go[7], Alpha Zero[8]的圍棋對弈等. 經典數據有許多處理和訓練方式, 如神經網絡、聚類等方法. 為了準確提取未知數據的特征, 訓練方式的選擇需要參考相應的數據類型. 當處理大規模的數據時, 為了獲取數據特征, 往往采取深度學習的學習方式, 如包含數十億權重的神經網絡[9], 這充分展示了深度學習在處理大數據時的效果.

當今的機器學習發展, 特別是在大數據的處理方面, 對經典計算機的運算能力有很高的需求.1965年戈登·摩爾提出摩爾定律, 指集成電路上可容納的元器件數目約每兩年增加一倍. 一方面, 在不久的將來隨著晶體管在芯片上的間距接近1 nm,接近傳統工藝制造的物理極限; 另一方面數據的爆炸式增長, 對算力需求越來越高. 于是為了應對大數據的處理, 需要一個創新的計算體系結構. 量子計算作為一種新的計算模型, 比起經典計算, 在一些特定算法上有著指數加速的能力, 有望為大數據的處理提供足夠的計算需求. 如果一個量子信息計算處理器能夠產生經典計算機難以模擬的統計模式, 那么量子計算與機器學習結合便可能識別經典機器學習難以識別的特征. 為此, 人們將量子運算和經典的機器學習相結合, 提出了機器學習的量子版本, 稱為量子機器學習, 并將這種寄希望于量子機器學習的優勢稱為量子計算在經典機器學習中潛在的加速能力[10]. 量子機器學習包括用經典機器學習的方法處理量子物理中的問題和用量子計算的方式解決經典機器學習的問題. 前者需要將量子物理中的量子態轉換為經典數據, 再用經典機器學習的方法來提取數據信息, 如構造經典神經網絡訓練這些經典數據后, 得到某些量子態的特征. 后者在處理經典數據時, 某些步驟中的計算過程可以通過量子態的酉變換來輔助實現, 這其中不可避免地需要將經典數據對應成量子態.

量子機器學習中, 需要運用量子計算機處理經典數據, 這涉及經典數據的在量子體系中的表示問題. 這種將經典數據映射到量子計算機中的過程,稱為態制備問題[11,12]. 態制備的種類有很多, 大部分是將經典數據轉換為了量子態, 也存在一些將經典數據映射到哈密頓量的方式. 態制備種類的選擇直接影響了執行機器學習算法的選擇, 這意味著不同的態制備方法決定了提取經典數據信息的差異,影響了后續在量子系統里的操作, 影響整個機器學習算法的計算復雜度. 同時, 態制備作為量子機器學習的其中一部分, 其制備精度和成功率會影響整個機器學習算法的有效性.

態制備問題不受限于機器學習的應用, 它同樣是一些算法的基礎, 如解線性方程組的HHL量子算法[13]. 基于解線性方程組的量子算法, 有量子主成分分析算法[14], 可用于聚類和特征識別; 也有支持向量機算法[15], 用于對大規模的數據分類問題.這類量子算法的共同點都是為了解決實際的經典問題, 需要以經典數據為輸入和輸出. 這可以分為三個步驟: 首先運用態制備將經典數據轉為量子態, 再用量子計算機對量子態進行酉變換, 最后多次地量子測量概率性得到一個經典結果. 整個算法的復雜度受各個步驟的影響, 本文僅列出不同態制備方式的復雜度. 如果考慮量子算法的復雜度, 可通過量子線路的語言, 對所需的基本量子操作, 即基本量子門計數得到所有門的個數. 類比于經典算法的分類方式, 量子算法分為不含黑箱(oracle)的顯式算法和含黑箱的算法. 前者的復雜度指的是所有基本量子門個數, 后者往往勿略黑箱的執行時間而考慮黑箱的執行次數, 稱為質詢復雜度. 一般地,若數據規模是O(N) 的, 量子基本門的時間層數是O(Poly(logN))的, 稱量子算法的執行時間是有效的. 在每個時間層, 允許多個量子比特同時執行一次量子基本門. 同樣的數據規模, 若用到的量子比特是O(Poly(logN)) 的, 稱量子算法的比特數是有效的. 量子基本門的個數受量子比特數和時間層數的影響, 在一個時間層至多有量子比特數的量子門同時執行, 故顯式算法的復雜度上界為量子基本門的時間層數與比特數的乘積.

從經典計算機到量子系統態制備的方式叫作編碼. 編碼的種類大體上可以分為三種, 分別是基底編碼、振幅編碼和量子抽樣編碼[12]. 基底編碼用于處理二值數據向量, 將數據編碼到量子態的基底上; 振幅編碼是最為常見的態制備方式, 將數據編碼到量子態的振幅上, 數據向量可以是連續變量,數據特征信息體現到量子態的振幅大小; 量子抽樣編碼可以看成前兩種編碼的結合, 是對在整個計算基基底的經典概率分布進行振幅編碼, 對于某個給定的經典概率分布, 量子抽樣編碼退化為了振幅編碼. 上述由經典數據編碼到量子態的過程, 在量子系統中也可以視為從初態到目標量子態的一種酉變換. 廣義上講, 可以稱從經典數據到酉變換的過程為編碼, 如由經典數據決定量子系統演化哈密頓量的方式也可以看成一種編碼, 這種編碼稱為哈密頓量編碼.

態制備中振幅編碼的相關工作最為豐富, 除了平凡的編碼方式, 振幅編碼可以從2002年Grover和Rudolph[16]的工作談起, 其將滿足條件可積的一種數據分布制備成了量子態, 制備過程依賴于經典函數的有效計算, 且沒有給出量子線路語言, 編碼的有效性需進一步探討. Kaye等[17]以類似的方式得到了任意量子態的制備, 給出了可稱之為含黑箱的量子線路. Soklakov和Schack[11]于2005年用其他形式的黑箱給出了在一定限制條件下的有效的概率性算法. 振幅編碼中不得不提到量子隨機存取存儲器(quantum random access memory,QRAM)的方法, 這是一種從已知量子態出發, 由經典數據直接得到新的量子態的過程.

本綜述簡要敘述各種態制備的編碼方式, 并給出一些簡單的例子. 根據各個編碼方式的適用情景, 對不同編碼進行比較, 列出態制備的復雜度,表明應謹慎樂觀對待量子態制備問題.

符號說明文中希爾伯特空間用H表示, 任意的單位化向量|ψ〉∈H 表示量子態, 其中|0〉=(1,0)T,|1〉=(0,1)T. 泡利算符用σx,σy和σz表示,在Bloch 球上, 單比特的繞A軸旋轉門RA(θ)=e-iθσA/2=cos(θ/2)I-isin(θ/2)σA, 其中A=x,y,z.

2 編碼方式

這里給出態制備的問題模型. 對給定的經典數據, 不妨假定數據集D?Rn是有限集,|D|=l, 每個數據x=(x1,···,xn)∈D, 用一個單射f將D的所有子集構成的集合, 記為 2D, 映射到某個希爾伯特空間Hm, 使得對D′?D,f(D′)∈Hm. 稱f為態制備, 其中Hm中的元素都視為單位向量, 對應量子態. 例如,D={x1=(1,0),x2=(0,1)}, 可以找到一種態制備的映射,使得f({x1})=|10〉 ,f({x2})=|01〉,f(D)=

2.1 基底編碼

這類編碼中, 限定所有數據是二元向量, 或二值化處理后的經典數據是二元向量, 即D?{0,1}n.對任意數據集的子集D′?D,xj=

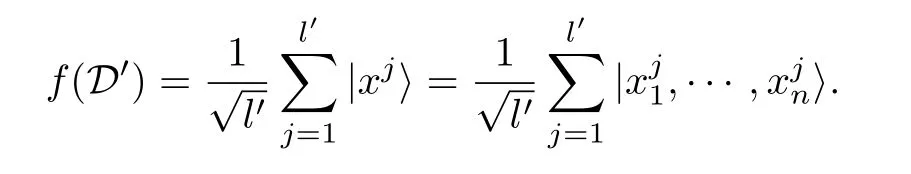
這種編碼方式將數據集中的所有數據, 編碼到量子態的計算基上, 等權疊加. 制備過程中用到的量子比特數為O(n). 制備的思路是運用迭代法.

以同樣的迭代方法, 可以得到|ψ1...l′〉 , 即得到f(D′).

2.2 振幅編碼

這類編碼要求的數據不再是二元向量, 可以是任意實數. 對于任何

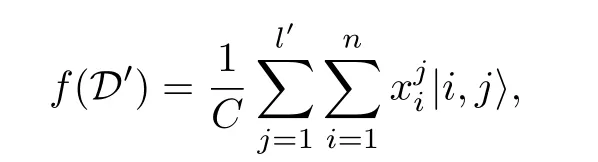
這里C為歸一化常數,可以看出, 如果對數據集中所有數據振幅編碼, 當ln是 2 的冪次時, 只需要 l og(ln) 個量子比特便可以編碼ln個振幅. 例如,ln=4 時, 只需制備一個2 bit的量子態, 使得在四個計算基|00〉,|01〉,|10〉 和|11〉上的振幅為數據大小即可. 振幅編碼問題可以簡化為, 給定一個單點集合X={x=(x0,···,xN-1)}?RN,N為 2 的冪次, 使得在忽略歸一化常數的條件下

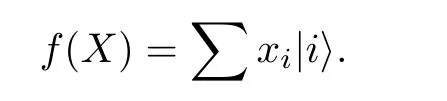
2.2.1 顯式的編碼

1)用 l ogN個量子比特編碼.

基本的想法是利用迭代法, 用部分量子態對新粒子多重控制操作, 直到全部粒子完成態制備. 這個算法的執行時間是O(N). 假定制備出的量子態的每個振幅的大小已知, 即每個計算基上測量得到相應的結果的概率已知, 并且我們定義邊際概率logN-1, 如圖1所示.

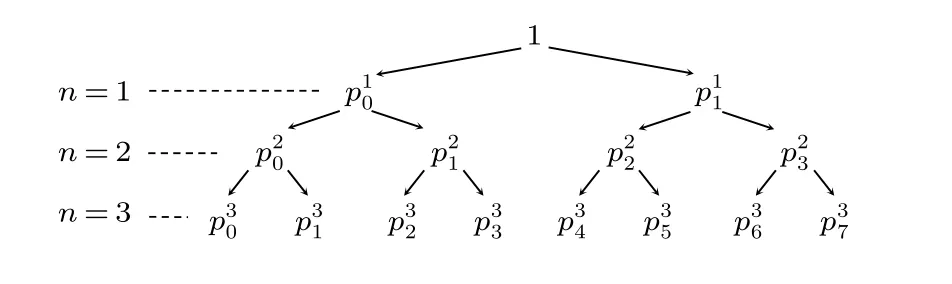
圖1 當 N =8 時所有的邊際概率Fig. 1. The marginal probabilities for N =8.

假定i=0,···,2k-1), 則態制備的整個迭代流程圖可以參看圖2.

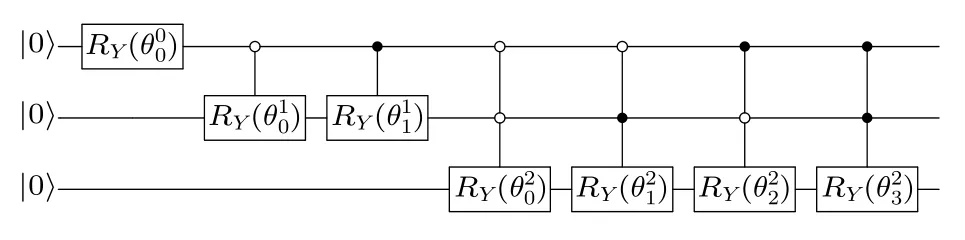
圖2 N =8 時用 O (N) 的時間制備f(X)Fig. 2. Preparation for f (X) in O (N) time for N =8.

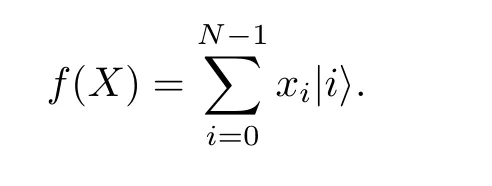
在用 l ogN個量子比特編碼時, 每個基底前的振幅都不能并行運算, 導致了這個方法的運行時間為O(N). 如果這些多重受控操作可以并行操作,運行時間將大大降低.

2)用N個量子比特編碼. 基于減少運行時間的考量, 可以增加量子比特, 使得編碼振幅的基底選擇性更多, 從而增加并行運算的可行性. 這里選取W態的基底, 得到態制備的映射為

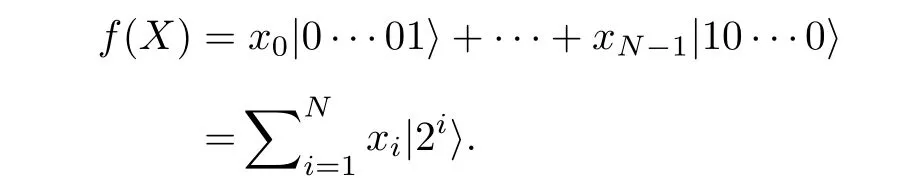
令

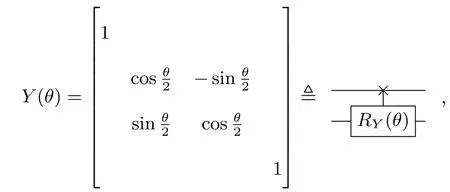
可以注意到Y(θ)|01〉=cos(θ/2)|01〉+sin(θ/2)|10〉 ,Y(θ)|10〉=-sin(θ/2)|01〉+cos(θ/2)|10〉, 這類似于對 單 比特量 子 門RY(θ) 在|0〉 和|1〉 上的操 作, 故將Y(θ) 定義為由符號“×” 控制的RY(θ) 量子門. 這里直接給出N=8 時的整個迭代過程, 詳見圖3.

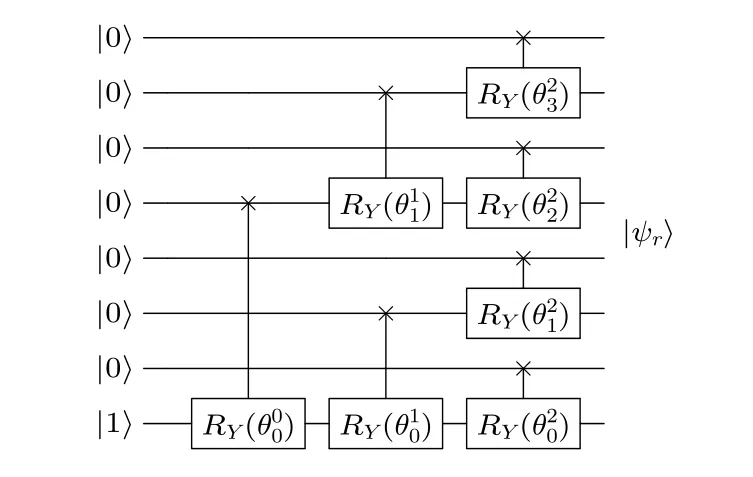
圖3 N =8 時用 O (logN) 的時間獲取振幅Fig. 3. Acquiring the amplitudes in O (logN) time for N=8.

2.2.2 含黑箱的編碼

這類編碼不考慮黑箱構造的問題, 有兩大類制備方案.

I) Grover等[16]和Kaye等[17]的工作

Grover在2002年提出將滿足條件可積的經典數據制備成量子態的方法. 給定一個離散概率分布目標制備等價于給定單點集{x=(x0,···,xN-1),xi≥0}, 滿足歸一化條件制備的思路與顯式編碼相同, 都是運用迭代法, 為了描述方便, 仍然采用邊際概率的記號

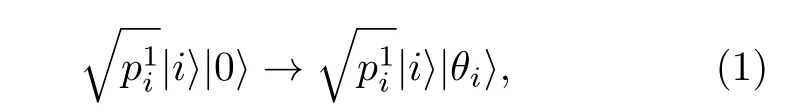
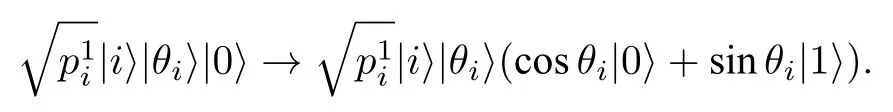
之后進行退計算操作, 將θi擦除, 這步操作的量子比特數量與執行時間及存儲θi相同, 同樣是含f的黑箱操作, 得到|ψ2〉.

運用迭代法, 由|ψk〉 得到|ψk+1〉 , 最終得到|ψlog2N〉 , 即目標量子態|ψ〉.

Kaye等[17]的態制備方法與Grover類似, 給出了量子線路的語言. 其中對存儲θi的步驟進行細化, 在已知|ψ〉 的前提下, 將(1)式改寫為

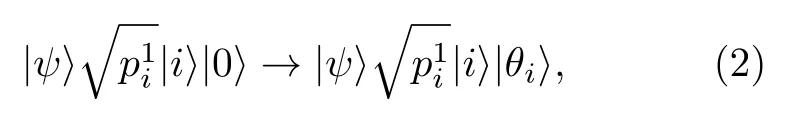
這步黑箱操作表明θi的獲得需要整個態|ψ〉 的各個分量的值, 并未給出黑箱操作的具體構造, 在這一點上與Grover的算法沒有本質區別.

評價含黑箱的算法復雜度, 通常不考慮黑箱以外的線路, 這是由于黑箱的結構相比于顯式的量子線路更為復雜. 如果同時考慮黑箱內部的執行時間和黑箱外的量子門執行時間, 對于任意N規模的量子態, 是不可能用O(n) 的量子比特在有效時間完成的. 因此, 我們往往考慮黑箱的執行次數, 稱為質詢復雜度, 以此來衡量含黑箱算法的計算復雜度. Kaye 的算法對于任意的量子態都可以制備,并且從含黑箱的角度看出是以(2)式為黑箱的振幅編碼, 該編碼方式具有有效的質詢復雜度. 不過,值得說明的是Grover和 Kaye的算法原文中并沒有指明是含黑箱的算法. 給定數據集X, 制備過程可以視為含黑箱的量子算法. 若是未指明某個數據集上的經典數據, 對數據集中的元素隨機化處理,如數據集中的元素滿足某種概率分布函數g, 對這種分布的態制備問題可能是有效的, 因為g的參數可能不依賴于n. 這種含黑箱的編碼比較廣泛, 將在2.3節的量子抽樣編碼中再次提及.

II) Soklakov和Schack[11]的工作

真正意義上經典的含黑箱的振幅編碼可參看Soklakov等的工作. 這類算法屬于概率性的量子算法, 態制備給出了理想態的近似量子態. 數據向量不局限于實空間, 即X={x=(x0,···,xN-1)}?CN,N為 2 的冪次, 這里xi=|xi|eiαi,αi∈[0,2π) , 但|xi|不可以全相等. 理想的量子態為

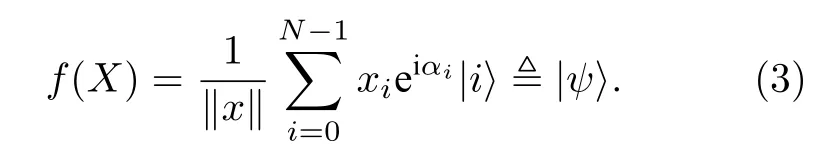
該編碼的執行時間受限于兩個因素. 一方面是數據集本身x各個分量實部的差異, 如果各個分量|xi|大小都比較接近, 那么編碼執行時間會很快. 另一方面是對制備量子態結果保真度和成功率的要求,如果對態制備的結果要求嚴苛, 會導致執行時間變慢. 令γ,λ,η∈(0,1) , 如果對任意的數據分量, 以不小于 1-γ的成功率制備的近似態為滿足, 所需要的計算復雜度為

算法的核心內容是選擇合適的黑箱, 對獲取目標量子態所有分量振幅的大小做分割, 并從振幅大分量向振幅小的分量標記, 最終用 Grover搜索算法, 將目標態的近似態以一定的成功率找到.

2.2.3 QRAM

量子隨機存取存儲器(QRAM)是類比于經典內存存取數據的一種裝置, 可以將經典數據存儲到相干的量子態各個分量地址中. 在讀取量子態的任意一個分量時, 每個分量地址上都需要附帶經典數據的信息:

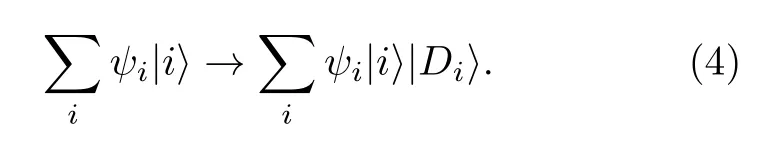
QRAM存取數據的過程中, 第一個寄存器存儲經典數據作為指標, 要求對任意量子態分量都需要存儲經典數據地址信息. 第二個寄存器是數據寄存器, 用于存儲經典數據X. 這種裝置類似于(1)式, (2)式的操作方式, 故一定程度上, QRAM的模型包含了Grover和Kaye等的態制備工作.例如在量子推薦系統算法中[19], 概率分布被提前儲存到QRAM中, Grover的算法也可以實現. 理論上, QRAM的模型可以通過增加大量的比特數來減小執行時間. QRAM通過二分的樹狀圖和桶隊結構(bucket-brigade)來實現, 這種實現方式可以做到O(n) 的時間復雜度, 但量子比特數是O(N)的. QRAM的量子線路語言實現方式種類較多[20,21]. 人們在后續的工作中更關心哪一種QRAM的實現方式更具有噪聲的抗性和可拓展性, Hann[22]給出了一種關于噪聲抗性的論證.

(1)式, (2)式以及QRAM的直接形式(4)式都是將經典數據存儲到輔助比特上, 每個分量對應的輔助比特上都有經典數據的信息. 特別地, 如果輔助比特可以寫成二進制數, 這種變換稱為數字編碼. 與之對應的, Mitarai稱振幅編碼為模擬編碼[23], 并介紹了數字編碼和模擬編碼的轉換關系.利用這種數模轉換的關系, 可以得到振幅編碼的具體形式.

具體來講, 如果QRAM的操作完成后, 振幅編碼可以通過條件受控和后選擇的方式得到振幅編碼的概率性量子算法. 給定數據集X, QRAM可以將x=(x0,···,xN-1) 存儲到等權疊加的量子態上, 忽略歸一化, 得到

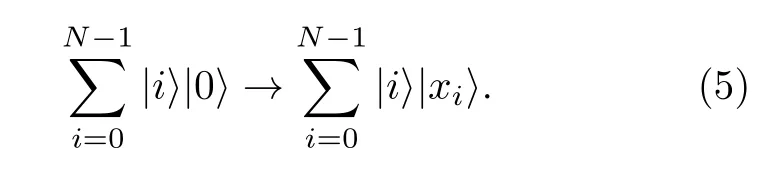
進行條件受控操作, 通過增加輔助比特和受控操作實現,

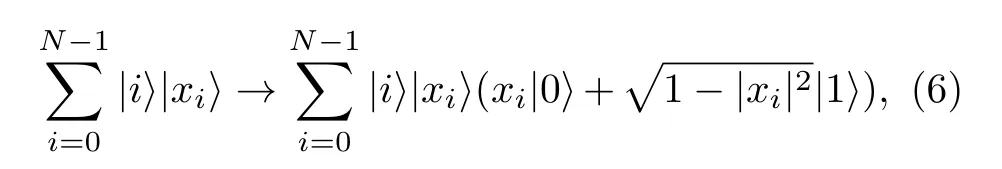
(6)式中的受控旋轉操作可以將xi表示為t比特的二進制數, 分別對輔助比特做控制RY(π/2t) 類似的操作來實現. 最后一步進行后選擇的操作, 對輔助比特進行測量, 當測量到|1〉 態時, 制備失敗. 需要重復這個算法的流程, 直到測量值|0〉. 當測量值為|0〉態時, 成功制備, 成功率可以計算, 得到

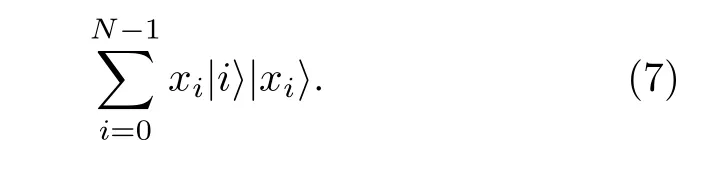
(7)式得到的量子態與目標態還多了數據寄存器的數據, 需要擦除. 這步擦除數據是退計算的過程,也是QRAM里(5)式的逆操作, 即

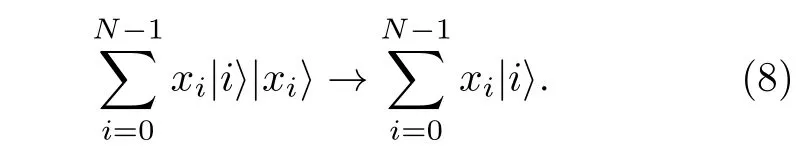
2.3 量子抽樣編碼

本節介紹基底編碼和振幅編碼的一種混合編碼方式——量子抽樣編碼. 振幅編碼的數據集X是單點集,X={x=(x0,···,xN-1)}, 如果用logN個量子比特, 時間復雜度為O(N). 在量子抽樣編碼中, 給定一種概率分布, 不妨假定為g(x′),x′∈[0,N], 表示量子態的在每個基底的概率為pi=數據集仍為單點集目標量子態是X對應的振幅編碼

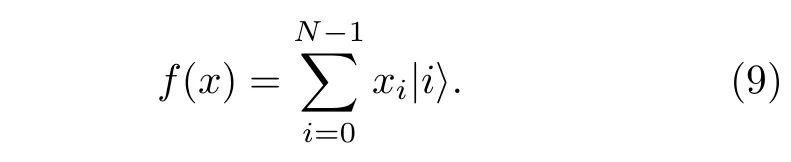
這類編碼的編碼技術是從已有的量子態出發, 根據經典數據的分布g(x′) 得到新的量子態, 與一般的振幅編碼相比, 這類編碼的g(x) 參數可能與N無關. 可以通過對分布函數g(x′) 做一些限制, 得到關于某些函數性質有關的態制備方法.

在 Grover等[16]的工作中, 作者進一步提出對于很大一類被稱為“對數凸”的函數, 都可以通過這種編碼方式進行制備, 這其中包括常見的正態分布和指數分布. 除了Grover的工作, Kitaev和Webb[24]也分析了高斯分布的量子態制備. 文獻[25]給出了一種基于矩陣積態(matrix product state)方法, 得到了當g(x′) 為光滑可微且導函數有界時的編碼方式. 該算法需要O(n) 個量子比特, 執行時間為O(n). 實驗方面Vazquez和Woerner[26]給出了基于量子振幅放大算法簡化態制備的方法, 并在IBM的物理比特上展示了實現了該算法.

以機器學習的方式研究這類情形的態制備問題有大量的工作, 如生成對抗網絡[27], 給定經典數據的分布, 利用含參數的量子線路生成一種量子分布, 再由對抗識別器對量子分布采樣, 反復調整, 直到識別不出經典數據分布與生成的分布, 訓練完畢. 數值模擬過程中所需要的量子門數量控制在O(P(n)). 也有其他機器學習相關的工作, 如Arrazola等[28]用含參線路在光量子計算機模擬器演示了許多量子態的生成, 如ON態和 GKP態.值得一提的是, 此類統計分布的態制備問題, 在量子蒙特卡羅模擬算法中處于非常核心的地位[29],而后者已經被證明在很多金融和其他模擬問題中顯示出量子優越性[30-32].

2.4 哈密頓量編碼

經典數據轉為量子態的另一種方案是將經典數據的信息編碼到某個量子系統的哈密頓量中,運用哈密頓模擬的方式代替將經典數據轉為量子態的方法[33]. 記經典數據集為X={x=(x0,···,xN-1)}, 記對應的哈密頓量為Hx, 表明哈密頓量依賴于經典數據的選擇. 則對于量子系統的初態|ψ〉, 演化時間為t, 得到演化后的量子態為

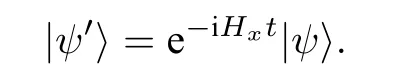
哈密頓量的演化過程可以由量子線路語言實現[18]. 考慮一個n量子比特的量子系統, 哈密頓量可以分解為一些哈密頓量的和, 即其中Hi為較易模擬的哈密頓量,L=O(P(n)). 由Trotter公式[33],

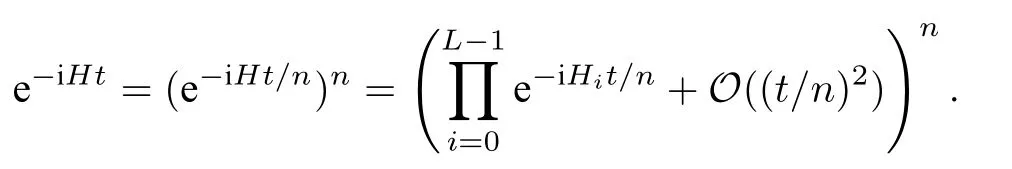
當n充分大時, 可以用多次的演化來實現量子模擬.Hi常見的選擇是泡利算符.

哈密頓量編碼的步驟分為兩大類. 一類是從哈密頓量H出發. 1) 由經典數據確定哈密頓量H, 如經典數據為動能、勢能函數決定的參量; 2) 在某個量子系統中選定基底, 確定哈密頓量的矩陣元;3) 哈密頓量模擬. 模擬過程包含哈密頓量的分解,需要確定Hi. Matto等[34]用格雷碼序的方式對經典數據進行哈密頓量編碼, 是一種比特數有效的編碼方案. 另一類是從分解后的哈密頓量Hi出發.1) 選定Hi, 由經典數據得到每個Hi的系數; 2) 在某個量子系統中選定基底, 確定哈密頓量Hi的矩陣元; 3) 得到總的哈密頓量, 即為經典數據的哈密頓量編碼. 例如用第二類的方法, 假定經典數據x=(x0,···,x4n-1), 我們將經典數據x編碼到n粒子哈密頓量中, 以泡利算符和單位算符在計算基上的表示為基底, 基底個數為 4n, 總的哈密頓量為

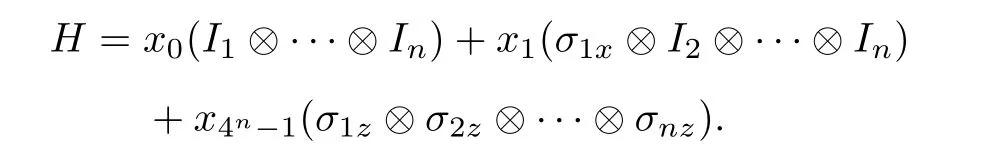
3 復雜度

當數據規模為O(N) 時, 基底編碼的執行時間為O(N) 次, 需要的量子比特數為O(N) , 復雜度為O(N2). 振幅編碼適用范圍廣, 其中顯式振幅編碼的復雜度為O(N)logN, 對于含黑箱的振幅編碼,僅考慮質詢復雜度, 可以做到有效制備, 即在一定條件下質詢復雜度可以達到O(log(N)) , 但黑箱的執行時間在實際操作中需要考量. QRAM的編碼方式從已知量子態獲取經典數據得到新的量子態,這個過程中需要O(N) 個量子比特, 但執行時間可以做到O(n). 而量子抽樣編碼也是直接從量子態出發, 比較目標量子態與量子初態的差異得到新的量子態, 比特數和時間有效性都可以實現, 這是由于給出的分布函數可以不依賴于數據量規模. 在哈密頓量編碼中, 哈密頓量的合理選擇可使得編碼方式中的比特數有效, 執行時間取決于哈密頓量的矩陣形式和哈密頓量模擬的精度. 進一步的, 考慮到量子比特數和時間執行次數的平衡和取舍, 噪聲抗性等因素, 態制備問題應該被仔細斟酌. 以上的復雜度分析可參看表1.

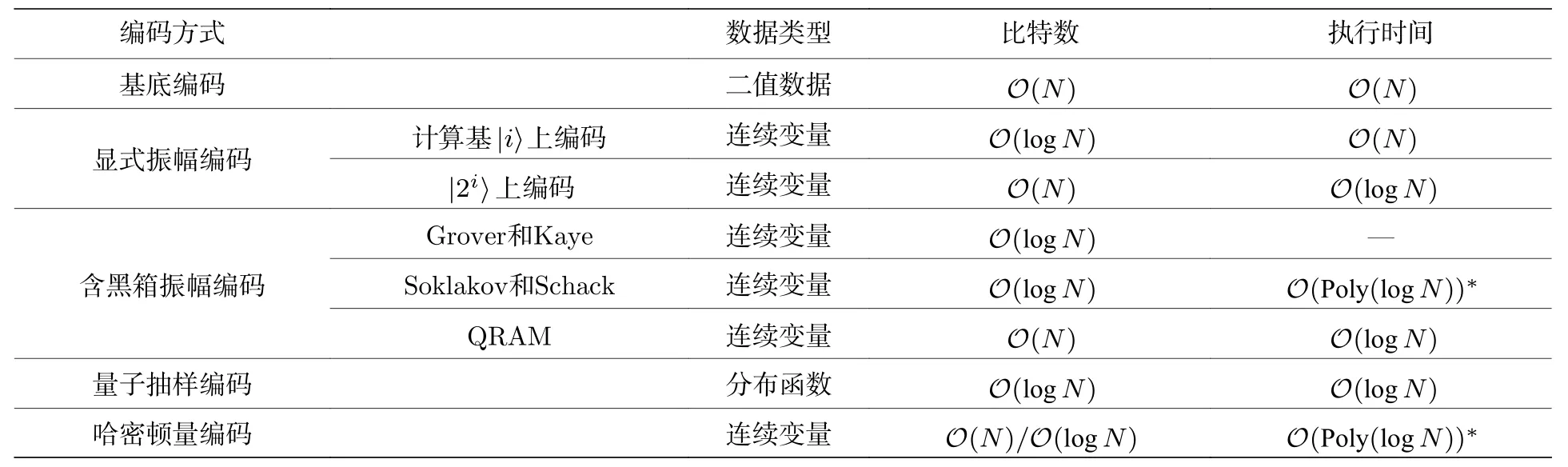
表1 態制備的不同編碼方式的復雜度分析Table 1. Complexity analysis of kinds of encoding methods for state preparations.

4 研究前景和展望

在未來, 經典計算機芯片的工藝制程接近摩爾定律極限, 經典計算機的算力發展達到瓶頸期. 而大數據的處理使得算力需求呈快速增長趨勢. 這之間算力的供需矛盾關系使得人們迫切地尋找新的計算模式. 研究量子機器學習的出發點是解決這種矛盾關系. 具體來說是希望在處理某一類問題時,量子機器學習的方法能夠大大縮短傳統經典機器學習需要的時間, 繼而在更廣泛的問題中表現出加速能力. 量子計算機的實用化受限于量子比特、量子門的質量和量子操作系統等諸多實驗因素, 故量子機器學習的研究大多停留在數值模擬或是構建理論模型的階段. 在這個大背景下, 人們不過多關注量子機器學習中的物理實現.

目前態制備問題里更受關注的是量子抽樣編碼, 其中涌現出了許多利用量子機器學習研究態制備的工作. 這種編碼方式通過經典神經網絡與含參量子線路的結合, 以監督學習的方式訓練參數, 不斷優化量子線路得到近似的目標量子態. 復雜度的分析通常考慮參數的數量, 但含參量子線路的表示能力與學習方式的選擇都會影響其編碼的有效性.這類工作比較豐富, 例如生成對抗網絡[27], 利用含參數的量子線路生成一種分布并由對抗識別器采樣, 機器學習的方式訓練參數, 直到對抗識別器識別不出目標分布與生成的分布; Arrazola等[28]采用的是光量子計算機模擬器, 利用自動微分法優化得到目標量子態; 最近Zhou等[35]提出了一種自動微分的量子含參線路, 可以優化得到任意的量子態.

另一方面, 態制備問題作為經典數據和量子態的橋梁, 在量子機器學習中的使用不可避免. 相較于經典計算機編碼數據的方式, 量子計算機在態制備時編碼數據的指數級加速能力是沒有問題的, 但這是以大量量子比特數為前提的實現方式. 研究量子機器學習的初衷是實用化解決經典問題, 更應該考慮其中的態制備方案的時間計算資源和空間計算資源. 對于復雜度的分析, 態制備的算法復雜度至少是數據自由度的量級, 既要分析時間復雜度,也要考慮量子比特數的規模. 單看時間復雜度, 得出具有加速能力的結論還不足以體現量子機器學習的能力, 分析時應該謹慎. 但同時也要樂觀對待量子機器學習的能力, 至少以發展的眼光去看待.例如, 大數分解的量子算法復雜度比已知最優的經典算法有指數級的提高, 而人們在大數分解算法提出前也不清楚量子計算的加速能力. 總的來說, 隨著量子計算機的發展特別是硬件水平的提升, 相信會有更多的人關注態制備問題.