地下黏彈性介質波動方程及波場數值模擬*

宋利偉 石穎 陳樹民 柯璇 侯曉慧 劉志奇

1) (東北石油大學物理與電子工程學院, 大慶 163318)

2) (東北石油大學地球科學學院, 大慶 163318)

3) (大慶油田有限責任公司勘探開發研究院, 大慶 163712)

實際介質普遍具有黏彈性, 波在傳播過程中常伴有能量的耗散、相位畸變和頻帶變窄等, 對于含有液體和氣體的介質, 衰減現象尤為突出. 由于經典的波動理論未考慮介質的黏彈性效應, 基于完全彈性假設的模擬波場和實際傳播特征之間的差異明顯, 波動理論在工程技術中的應用效果還有提升的空間. 在巖石物理中,品質因子Q是量化地震衰減強度的參數, 為了研究波在地下介質中的傳播規律, 本文從常Q理論出發, 在黏彈性介質頻散關系中, 利用多項式擬合和Taylor展開法將頻率的分數階轉化為整數階, 進而推導了時間域復數形式的地下黏彈性介質波動方程. 該近似處理避免了頻散關系經域轉換后出現分數階時間微分項, 能有效地降低計算成本. 最后, 采用有限差分法聯合偽譜法對均質模型實現了波場的數值模擬, 驗證了方程的有效性.

1 引 言

地下介質普遍具有黏彈性, 波在傳播過程中部分能量轉變成熱, 波場特征會發生明顯變化, 如振幅衰減、相位畸變和頻帶變窄等. 當地層中含有氣體或液體時, 黏彈性效應更加突出. 忽略黏彈性的波場模擬易導致波場描述失真, 不利于工程技術中的應用[1-4], 因此有必要開展黏彈性介質波動理論及波場數值模擬的研究.

在巖石物理中, 品質因子Q用于計算應力與應變之間的相位差, 是度量地震波衰減特征的參數. Liu等[5]利用廣義標準線性體建立了不依賴頻率的Q模型, 解釋了地震波能量衰減和相位畸變的原因, 理論上Q值與實際介質的匹配度取決于線性體的數目和組合方式[6,7]. Kjartansson[8]在衰減系數和頻率成線性關系的假設下建立了常Q模型, 由于頻散關系的數學形式簡單, 在地震資料處理中得到了廣泛關注. 從常Q模型的本構關系出發, Carcione等[9,10]推導了黏彈性介質波動方程,并采用Grünwald-Letnikov近似實現了地震波場數值模擬, 由于方程中分數階時間微分項的計算依賴于歷史時刻波場, 因此需要保存全時程波場, 計算成本較高. 雖然短時截斷法和內部變量法能降低內存的占用[11,12], 但依然難以應對大尺度模型.Yang和Zhu[13]推導了分數階拉普拉斯算子的黏彈性介質波動方程, 并應用于地下構造成像中.

波動方程是雙曲線偏微分方程[14-17], 常用的數值模擬方法有偽譜法、有限元法和有限差分法.有限差分法無需數據域的轉換, 且計算效率高, 是波動方程數值模擬中最常用的算法[18,19], 為了在相同計算量的情況下提高數值模擬精度, 先后發展了交錯網格和旋轉交錯網格[20,21]. 偽譜法通過Fourier變換實現, 相當于無限階差分算子精度, 計算效率不及有限差分法[22]. 有限元法的優勢是網格剖分靈活, 能模擬復雜介質中的波傳播, 但計算成本較高[23].

本文基于Kjartansson提出的常Q模型, 建立了黏彈性介質波動方程, 研究了波動方程的數值模擬方法, 通過數值實驗分析了品質因子Q對波場振幅、相位和頻帶的影響.

2 波動方程建立

在Kjartansson[8]提出的常Q模型中, 模量M(ω)在頻率域的形式為

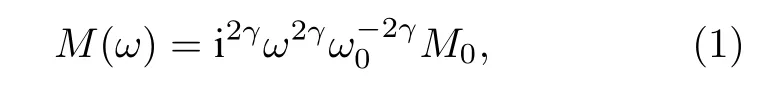
其中ω0是參考頻率;M0是模量;ω是頻率; i 是 虛數單位;γ與品質因子Q相關, 可通過下式確定[8]:

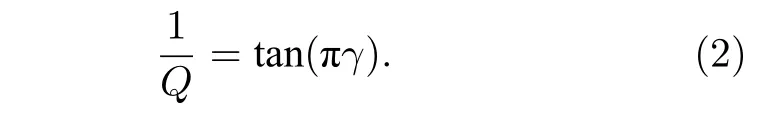
式中, πγ的物理意義是介質應力和應變之間相位差.

在地下黏彈性介質中波速vc與量M(ω) 的關系為[24]

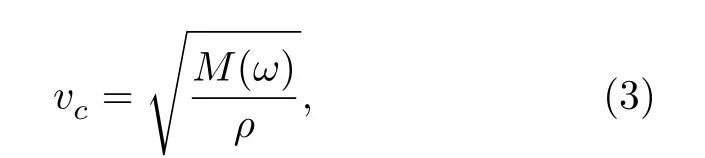
式中,ρ為介質密度. 相速度vp可利用下式計算,

式中,kR是波數k的實部, 利用等價關系i=cos(π/2)+isin(π/2)/2 ,k的實部kR和虛部kI根據(5)式和(6)式確定,

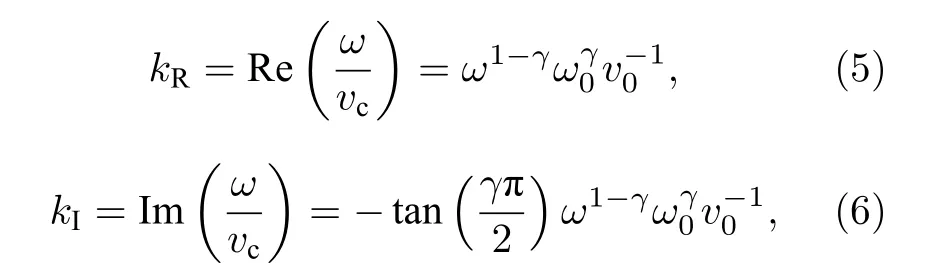
式中, Re和Im分別為取實部和虛部算子;v0=是在參考頻率處的相速度. 將(5)式代入(4)式可得

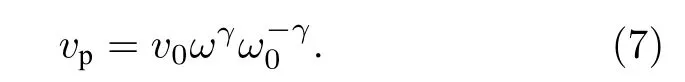
類似于彈性介質, 在黏彈性介質中波的頻散關系可表示為

將(1)式和(3)式代入(8)式有

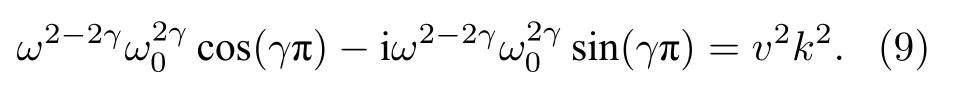
式中,v2=M0/ρ,v是Q趨于無窮大時的相速度,即介質趨于彈性介質時波的相速度. 若將(9)式從頻率-波數域變換至時間-空間域, 可得含有分數階時間微分的波動方程, 雖然采用Grünwald-Letnikov近似能實現分數階微分項的計算, 但該方法需保存歷史時間波場. 為此, 將(9)式等號左側第一項進行多項式擬合有

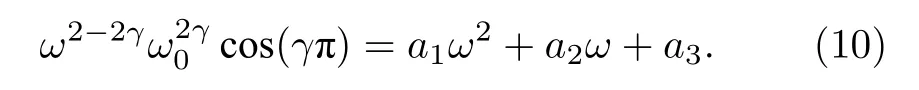
式中,a1,a2和a3為擬合系數, 表1提供了參考頻率為50 Hz時不同品質因子Q對應的擬合系數.當Q= 30時, (10)式擬合曲線如圖1所示, 圖中實心點是理論數值, 實線為擬合曲線, 以上擬合均是將頻率轉換至圓頻率所得.

表1 不同Q值擬合系數Table 1. Fitting coefficients of different Q values.

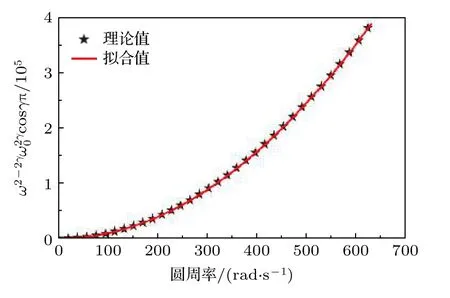
圖1 擬合曲線 (Q = 30)Fig. 1. Fitting curve (Q = 30).

(9)式中等號左側第二項中 iω經Fourier變換是時間的一階微分算子, 為了使剩余的ω1-2γ易于計算, 先對k2γ-1進行處理,

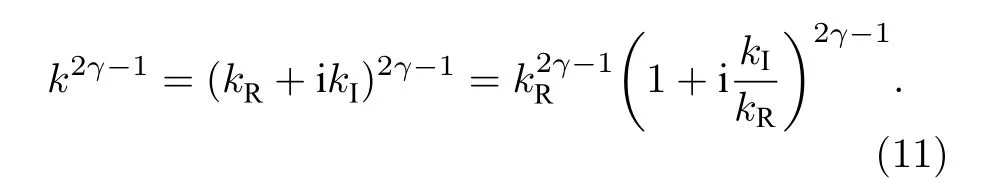
將(5)式和(6)式代入(11)式得

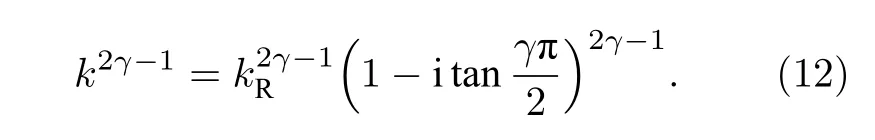
對于弱衰減介質有γ?1 , 利用Taylor展開可將[1-itan(γπ/2)]2γ-1表示為

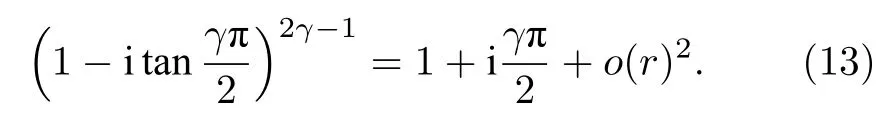
忽略(13)式的高階無窮小量后代入(12)式有

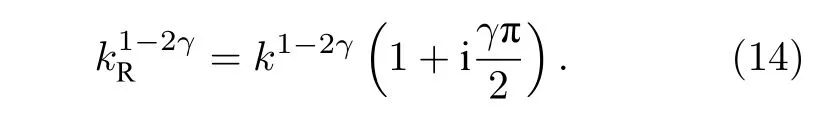
(4)式的等價形式為

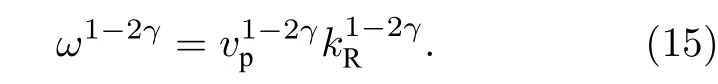
根據(7)式, 當參考頻率接近于波的頻率時, 有vp≈v0, 將(14)式代入(15)式為

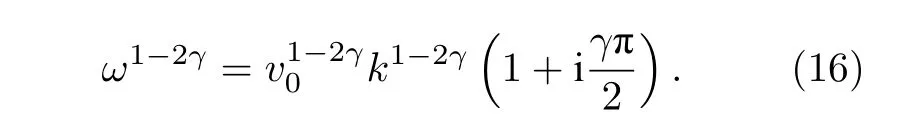
將(10)式和(16)式代入(9)式有

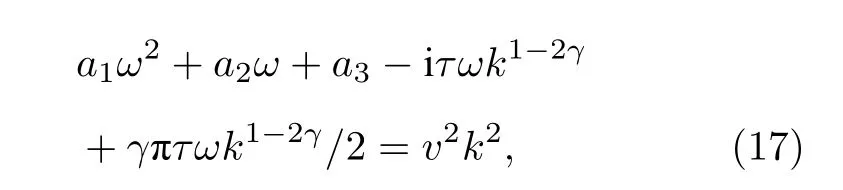
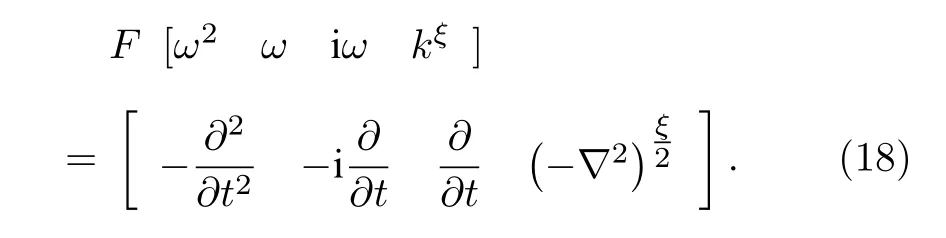
根據Fourier變換的微分性質, (18)式給出了算子在頻率-波數域和時間-空間域的對應關系,F為Fourier變換算子,?是拉普拉斯算子. 將(17)式乘頻率-波數域波場后, 經域轉換可得時間-空間域地下黏彈性介質波動方程:

(19)式中,u是復數波場, 取其實部即物理意義上的波場. 為了在數值模擬中研究波動方程中各項對波場的主控因素, 可將(19)式改寫為

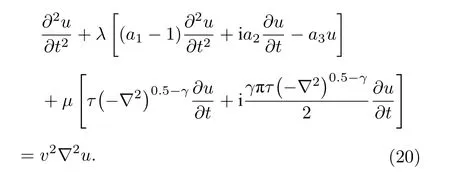
(20)式中參數λ和μ的取值為1或0, 兩參數組合可形成四個方程, 當λ=1,μ=1 時, (20)式和(19)式等價; 當λ=0,μ=0 時, (20)式退化為聲波方程.

3 波場遞推公式

本文采用二階精度有限差分法求解(19)式中的時間微分項, 其離散格式為

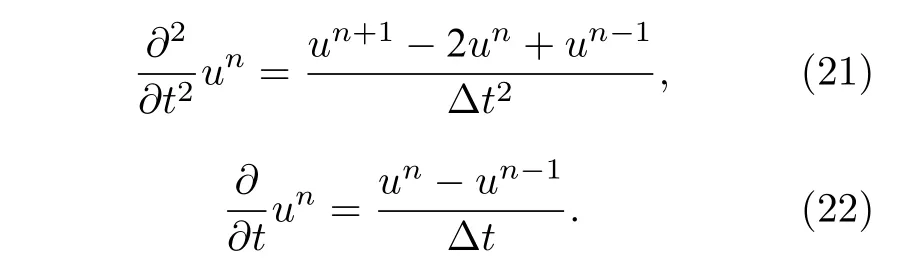
式中,n為時間節點; Δt是時間采樣間隔.

(19)式中的空間微分項采用偽譜法計算, 先通過Fourier變換將時間-空間域波場轉換至波數域, 與波數k和拉普拉斯算子的階數作用后, 再經反Fourier變換即可實現求解[25,26]. 以上過程可用(23)式表示:

結合(21)式、(22)式和(23)式, 波動方程(19)式的波場遞推公式為

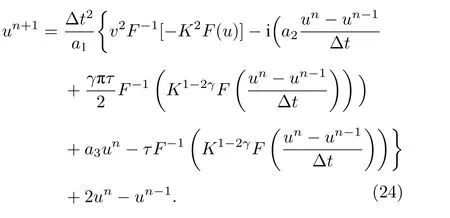
4 數值實驗

為研究地下黏彈性介質中波的傳播規律, 設計水平和垂直方向的距離為3.8 km的均質模型, 空間網格間距為10 m, 波在參考頻率50 Hz處的相速度為2216 m/s. 利用主頻是20 Hz的Ricker子波作為激發震源, 其振幅峰值為1 Pa, 時間采樣間隔1 ms, 子波的函數形式為

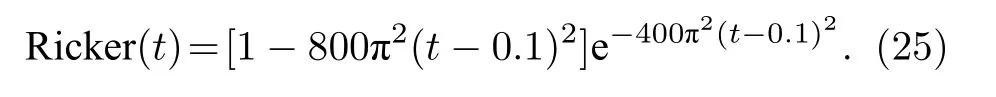
震源位于模型中央位置, 距離震源0.6 km處布置檢波器, 數值實驗模型如圖2所示. 設置模型品質因子Q為20, 編程驗證(19)式的有效性和數值模擬方案的可行性. 圖3為600 ms的波場, 由于介質中不含波阻抗界面, 因此波場特征是外擴的圓.在模型垂直方向1.9 km處, 水平方向0—3.8 km范圍分別提取500和600 ms波場, 如圖4所示,隨著時間推移, 波場的能量由1.9 km處向外傳遞,受到介質的吸收衰減, 波場的振幅明顯變小.

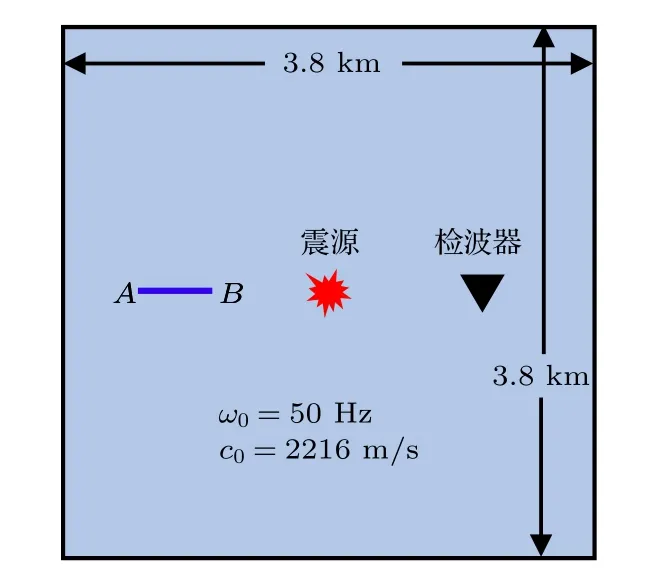
圖2 數值模擬模型Fig. 2. Numerical simulation model.

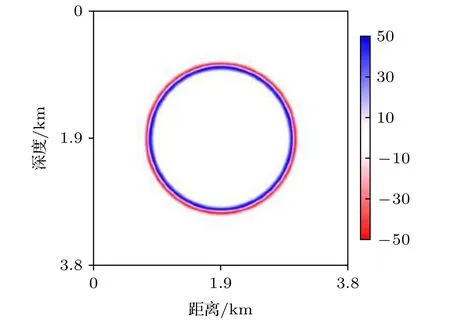
圖3 600 ms波場快照Fig. 3. Wavefield snapshot at 600 ms.

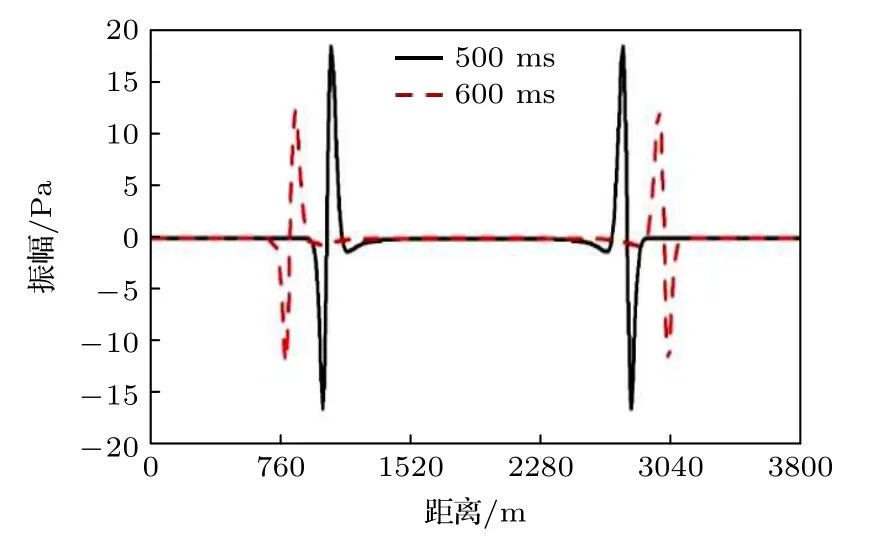
圖4 不同時刻的1維波場Fig. 4. One dimensional wavefield at different times.

介質的黏彈性不僅衰減波場的振幅, 而且影響相位和頻帶. 現采用不同Q值實施波場模擬, 檢波器從震源激發時開始采集信息, 直至1000 ms結束, 在模擬區域外側添加吸收衰減層以避免邊界產生虛假反射. 圖5是在相同傳播路徑下, 不同Q值所對應的記錄, 由于檢波器接收的信息集中在380 ms, 排除無效信息僅對200至600 ms記錄顯示,Q值由30變為10后, 波場的振幅明顯減小,相位發生畸變. 圖5中兩記錄的歸一化頻譜如圖6所示,Q值影響了記錄頻帶的特征, 主頻由初始的20 Hz分別降至15和10 Hz. 在Kjartansson提出的常Q模型中,Q的減小對應著應力和應變之間的滯后變大, 進而介質對波場的吸收衰減變強, 此外該模型的假設是衰減系數與波場的頻率成正比關系, 即低頻成分的衰減比高頻成分弱, 通過數值實驗表明, 建立的波動方程能夠準確地描述波場的衰減規律, 且數值模擬方案可行.

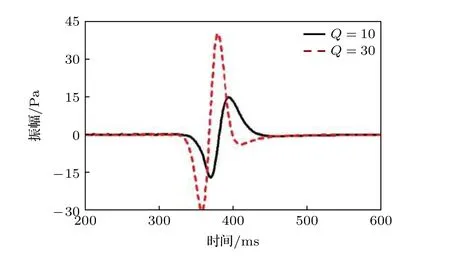
圖5 波場記錄Fig. 5. Wavefield record.

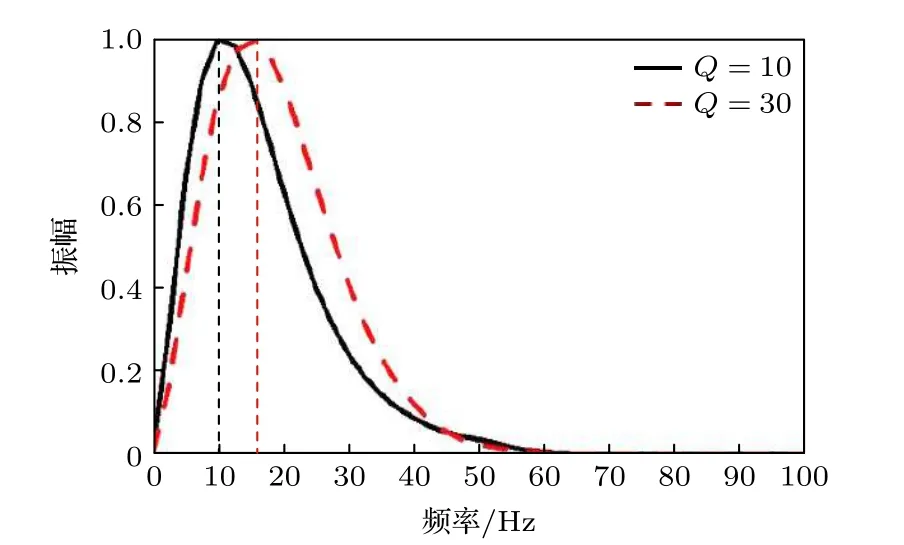
圖6 記錄頻譜Fig. 6. Record spectrum.

為了對比分析(20)式中各項對波場的主控因素, 采用控制參數λ和μ的方式對方程實施數值模擬, 圖7(a)—(d)分別對應λ=0,μ=0 ,λ=0,μ=1 ,λ=1,μ=0 和λ=1,μ=1 的 截 取 波 場,圖7(a)與圖7(b)和圖7(c)的差異分別在于振幅和相位, 圖7(a)和圖7(d)在振幅和相位上均有差異. 基于以上研究, (20)式中等號左側第二項主控相位畸變, 第三項主控振幅衰減. 圖8為4個波場的局部(圖2中A點至B點)單道顯示, 該圖展示了彈性介質波場經振幅衰減和相位畸變后演變為黏彈性介質波場的過程.

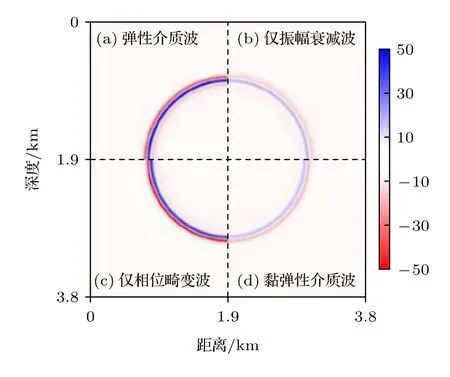
圖7 組合波場Fig. 7. Combined wavefield.

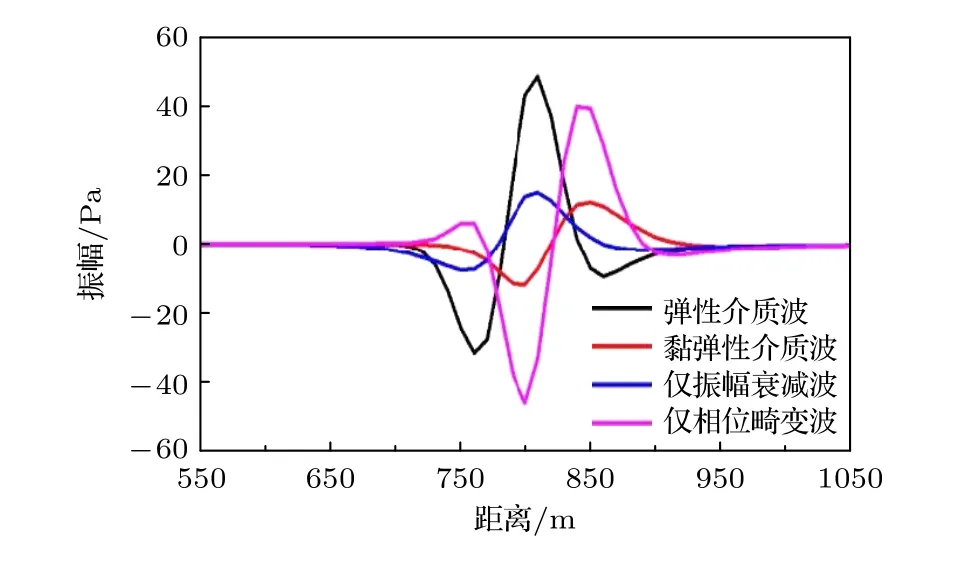
圖8 部分波場Fig. 8. Part wavefield.

為了測試數值方法對于復雜模型的有效性, 進行了波場數值模擬. 采用模型在水平和垂直方向的網格點數分別為401和301, 網格間距為10 m, 即水平距離為4 km, 垂直深度為3 km, 模型速度分布在2500至3500 m/s區間, 以層狀構造為主, 如圖9(a)所示, 品質因子Q取25. 震源布置在模型中央, 三個不同時刻的波場如圖9(b),(c)所示. 隨著時間遞增, 波場能量逐步外擴, 由于介質的黏滯性效應, 波場振幅出現了衰減特征. 通過測試表明,構建的黏彈性介質波動方程能刻畫波傳播至波阻抗界面所產生的透射波和反射波.

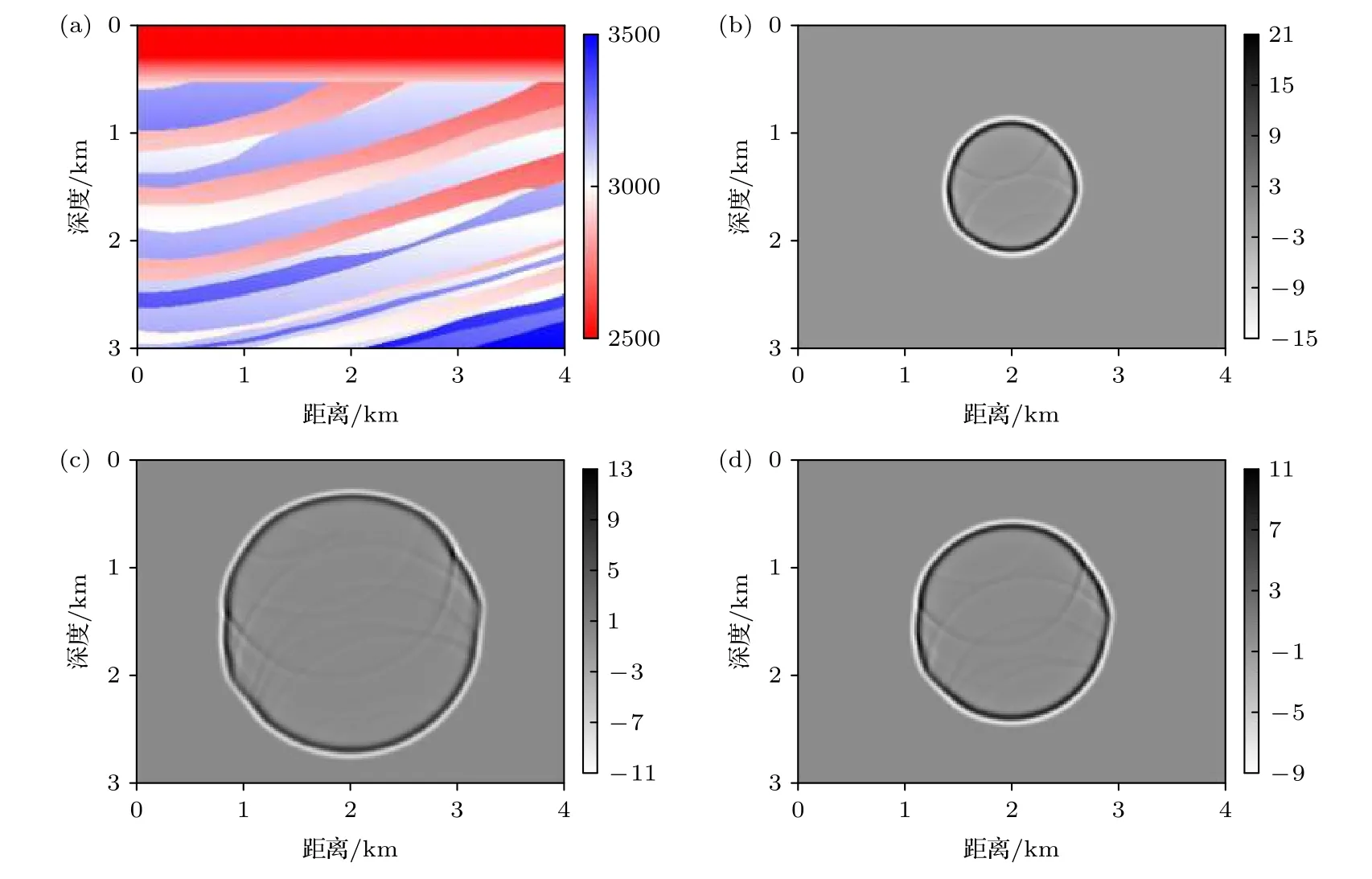
圖9 復雜模型波場模擬 (a) 速度模型; (b) 0.3 s波場; (c) 0.4 s波場; (d) 0.5 s波場Fig. 9. Wavefield simulation for the complex model: (a) Velocity; (b) wavefield at 0.3 s; (c) wavefield at 0.4 s; (a) wavefield at 0.5 s.

5 結 語

本文在常Q理論基礎上, 建立了黏彈性介質波動方程, 該方程能解耦振幅衰減和相位畸變效應, 有助于分析介質中的復雜波場現象, 可為地震資料處理提供理論基礎. 需要注意的是方程中拉普拉斯算子的階數是Q的函數, 偽譜法僅能處理Q場為常數的情況, 對于Q場較平滑的介質, 可將Q場的平均應用至全局. 為了應對Q場具有強非均質性的波場模擬, 如何將Q從拉普拉斯算子的階數中分離值得深入研究.