一類(lèi)影響網(wǎng)絡(luò)能控性的邊集研究*

2021-08-05 07:36:36趙國(guó)濤王立夫關(guān)博飛

物理學(xué)報(bào) 2021年14期

趙國(guó)濤王立夫關(guān)博飛

(東北大學(xué)秦皇島分校控制工程學(xué)院, 秦皇島 066004)

應(yīng)用復(fù)雜網(wǎng)絡(luò)描述大規(guī)模復(fù)雜系統(tǒng)間的相互作用已被廣泛接受, 網(wǎng)絡(luò)中某些邊遭受攻擊或破壞會(huì)使網(wǎng)絡(luò)不能控. 然而哪些邊失效后會(huì)對(duì)網(wǎng)絡(luò)能控性造成影響? 針對(duì)這一問(wèn)題, 本文首先提出了類(lèi)關(guān)鍵邊集的概念,并給出了類(lèi)關(guān)鍵邊集的判定定理. 然后通過(guò)建立類(lèi)關(guān)鍵邊集失效模型, 來(lái)研究類(lèi)關(guān)鍵邊集失效對(duì)網(wǎng)絡(luò)能控性的影響. 最后將類(lèi)關(guān)鍵邊集失效、隨機(jī)失效、按度失效和按介數(shù)失效進(jìn)行對(duì)比, 驗(yàn)證了無(wú)論是在模型網(wǎng)絡(luò)(ER隨機(jī)網(wǎng)絡(luò)、BA無(wú)標(biāo)度網(wǎng)絡(luò)、隨機(jī)三角形網(wǎng)絡(luò)和隨機(jī)矩形網(wǎng)絡(luò)), 還是26種不同領(lǐng)域的實(shí)際網(wǎng)絡(luò)中, 類(lèi)關(guān)鍵邊集失效對(duì)網(wǎng)絡(luò)能控性的破壞力最大, 同時(shí)該結(jié)果為網(wǎng)絡(luò)邊攻擊提供了一種新方法.

1 引言

隨著社會(huì)和科學(xué)技術(shù)的不斷發(fā)展, 電力網(wǎng)絡(luò)、社會(huì)關(guān)系網(wǎng)絡(luò)、交通網(wǎng)絡(luò)和生物網(wǎng)絡(luò)等大型網(wǎng)絡(luò)漸漸進(jìn)入我們的視線. 起初人們對(duì)于復(fù)雜網(wǎng)絡(luò)的關(guān)注點(diǎn)主要集中在拓?fù)浣Y(jié)構(gòu)特征上, 如網(wǎng)絡(luò)的小世界特性[1]、無(wú)標(biāo)度特性[2]等. 而研究復(fù)雜網(wǎng)絡(luò)的主要目的是控制網(wǎng)絡(luò)的行為, 減少不必要的損害, 更好地為社會(huì)服務(wù), 因此復(fù)雜網(wǎng)絡(luò)能控性受到越來(lái)越多學(xué)者的關(guān)注[3,4]. Lin[5]首次提出了結(jié)構(gòu)能控性理論,Liu等[6]利用圖的最大匹配計(jì)算網(wǎng)絡(luò)的驅(qū)動(dòng)節(jié)點(diǎn),解決了有向網(wǎng)絡(luò)的最小輸入問(wèn)題. 然而有些網(wǎng)絡(luò),僅僅通過(guò)給驅(qū)動(dòng)節(jié)點(diǎn)添加輸入仍無(wú)法使網(wǎng)絡(luò)結(jié)構(gòu)能控, 為了求解使網(wǎng)絡(luò)結(jié)構(gòu)能控的最小受控節(jié)點(diǎn),Pequito等[7]提出了一種結(jié)構(gòu)能控性框架, Yin和Zhang[8]給出一個(gè)帶有約束的數(shù)學(xué)模型. 以上針對(duì)的是有向網(wǎng)絡(luò)能控性, 對(duì)于無(wú)向網(wǎng)絡(luò)的控制,Yuan等[9]利用PBH判據(jù)提出復(fù)雜網(wǎng)絡(luò)的嚴(yán)格能控性判據(jù), 該理論適用于任意結(jié)構(gòu)和邊權(quán)值的網(wǎng)絡(luò), 解決了無(wú)向網(wǎng)絡(luò)的能控性問(wèn)題. 根據(jù)網(wǎng)絡(luò)能控性衍生出來(lái)的問(wèn)題, 例如最小化[10,11]、邊控制[12]和對(duì)稱網(wǎng)絡(luò)能控性[13]的研究, 都為復(fù)雜網(wǎng)絡(luò)能控性的發(fā)展提供了新的思路. 與此同時(shí), 對(duì)實(shí)際網(wǎng)絡(luò)能控性的研究也從未止步, 例如交通網(wǎng)絡(luò)能控性[14,15]、腦網(wǎng)絡(luò)能控性[16]、電力網(wǎng)絡(luò)能控性[17]等, 都具有重要的現(xiàn)實(shí)意義.

通過(guò)對(duì)網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu)的研究可以更好地認(rèn)識(shí)和利用網(wǎng)絡(luò). 人們對(duì)網(wǎng)絡(luò)中節(jié)點(diǎn)屬性的研究取得一些成果, 文獻(xiàn)[18]通過(guò)節(jié)點(diǎn)分類(lèi)發(fā)現(xiàn)了網(wǎng)絡(luò)的雙峰現(xiàn)象, 文獻(xiàn)[19, 20]通過(guò)節(jié)點(diǎn)分類(lèi)解決了增長(zhǎng)網(wǎng)絡(luò)能控性問(wèn)題. 但是在邊屬性方面的研究相對(duì)較少,Liu等[6]根據(jù)邊失效后對(duì)網(wǎng)絡(luò)驅(qū)動(dòng)節(jié)點(diǎn)個(gè)數(shù)的影響, 將邊分為三類(lèi): 關(guān)鍵邊、冗余邊和普通邊.

當(dāng)一個(gè)網(wǎng)絡(luò), 由于自身原因或外部攻擊, 導(dǎo)致某些邊失效時(shí), 可能使整個(gè)網(wǎng)絡(luò)不能控, 因此網(wǎng)絡(luò)能控魯棒性受到越來(lái)越多的關(guān)注. 對(duì)于網(wǎng)絡(luò)邊攻擊, 最常見(jiàn)的攻擊方法有隨機(jī)、按度和按介數(shù)攻擊.例如, Ruths等[21]研究了在給定一組驅(qū)動(dòng)節(jié)點(diǎn)的前提下, 邊移除對(duì)網(wǎng)絡(luò)受控節(jié)點(diǎn)數(shù)量的影響.Lu和Li[22]研究了將邊按隨機(jī)攻擊、初始度攻擊、初始介數(shù)攻擊和重新計(jì)算度攻擊、重新計(jì)算介數(shù)攻擊對(duì)網(wǎng)絡(luò)能控性的影響, 結(jié)果表明重新計(jì)算比按初始值攻擊邊對(duì)網(wǎng)絡(luò)能控性損害更大. Thomas等[23]分析了在基于度和隨機(jī)的邊攻擊下, 用能控性和可達(dá)性來(lái)度量每次攻擊后受控節(jié)點(diǎn)位置的改變情況.Chen等[24]在6種有向模型網(wǎng)絡(luò)中研究了邊在按隨機(jī)攻擊、重新計(jì)算度攻擊、重新計(jì)算介數(shù)攻擊時(shí),對(duì)能控性的影響, 并展示了多環(huán)結(jié)構(gòu)在網(wǎng)絡(luò)中的良好性能. 以上的研究都沒(méi)有考慮網(wǎng)絡(luò)中某條邊失效后對(duì)周?chē)叺挠绊? 因?yàn)榫W(wǎng)絡(luò)復(fù)雜的拓?fù)浣Y(jié)構(gòu), 有時(shí)候某些邊的失效可能引發(fā)局部的故障, 進(jìn)而導(dǎo)致整個(gè)網(wǎng)絡(luò)崩潰[25,26], 因此Nie等[27]研究了單邊攻擊和邊級(jí)聯(lián)失效對(duì)網(wǎng)絡(luò)能控性的影響, 并且發(fā)現(xiàn)在無(wú)標(biāo)度網(wǎng)絡(luò)中, 級(jí)聯(lián)失效并不意味著驅(qū)動(dòng)節(jié)點(diǎn)的增加. 不同于以往基于常見(jiàn)的模型網(wǎng)絡(luò)(隨機(jī)網(wǎng)絡(luò)、小世界網(wǎng)絡(luò)和無(wú)標(biāo)度網(wǎng)絡(luò)等)的研究, Lou等[28]提出了q-snapback網(wǎng)絡(luò)模型, 并與multiplex congruence網(wǎng)絡(luò)、無(wú)標(biāo)度網(wǎng)絡(luò)進(jìn)行對(duì)比, 研究了基于目標(biāo)和隨機(jī)邊攻擊下的網(wǎng)絡(luò)魯棒性. 除了研究網(wǎng)絡(luò)的單邊失效, Shang[29]通過(guò)引入子圖魯棒性, 建立了一個(gè)分析框架來(lái)研究?jī)深?lèi)子圖在隨機(jī)攻擊、局部攻擊和目標(biāo)攻擊下的魯棒性.

通過(guò)以上分析可知, 當(dāng)前網(wǎng)絡(luò)結(jié)構(gòu)與能控性關(guān)系的研究, 主要集中在具有某種網(wǎng)絡(luò)拓?fù)鋵傩?度、介數(shù)等)的單個(gè)節(jié)點(diǎn)或邊失效對(duì)網(wǎng)絡(luò)能控性的影響上, 缺少一種直接影響網(wǎng)絡(luò)能控性的方法. 本文主要研究了一類(lèi)影響網(wǎng)絡(luò)能控性的邊集—“類(lèi)關(guān)鍵邊集”, 通過(guò)邊分類(lèi)和節(jié)點(diǎn)分類(lèi)得到了類(lèi)關(guān)鍵邊集的判定定理, 給出類(lèi)關(guān)鍵邊集失效模型, 并推導(dǎo)出失效的理論函數(shù). 通過(guò)將類(lèi)關(guān)鍵邊集失效和常見(jiàn)的3種邊失效方式(隨機(jī)失效、按度失效、按介數(shù)失效)對(duì)比, 在4種模型網(wǎng)絡(luò)(ER 隨機(jī)網(wǎng)絡(luò)、BA無(wú)標(biāo)度網(wǎng)絡(luò)、隨機(jī)三角形網(wǎng)絡(luò)和隨機(jī)矩形網(wǎng)絡(luò))和實(shí)際網(wǎng)絡(luò)中進(jìn)行邊攻擊, 分析類(lèi)關(guān)鍵邊集失效對(duì)網(wǎng)絡(luò)能控性的影響.

本文在論述時(shí)安排如下: 第2節(jié)主要介紹復(fù)雜網(wǎng)絡(luò)能控性的基本概念和網(wǎng)絡(luò)能控魯棒性指標(biāo);第3節(jié)根據(jù)節(jié)點(diǎn)分類(lèi)和邊分類(lèi), 提出類(lèi)關(guān)鍵邊集的概念, 給出類(lèi)關(guān)鍵邊集失效模型, 并推導(dǎo)其失效后的理論曲線; 第4節(jié)研究在模型網(wǎng)絡(luò)和實(shí)際網(wǎng)絡(luò)中不同邊失效方式下對(duì)網(wǎng)絡(luò)能控性的影響; 第5節(jié)對(duì)論文的成果進(jìn)行總結(jié), 并且給出今后的研究方向.

2 復(fù)雜網(wǎng)絡(luò)能控性

2.1 定義

對(duì)于有向網(wǎng)絡(luò)G(A)=(X,E) , 其中節(jié)點(diǎn)集X={x1,x2,...,xN}, 邊集E={e1,e2,···,eM}.A=(aij)N×N表示有向網(wǎng)絡(luò)G(A) 的鄰接矩陣,aij表示節(jié)點(diǎn)j對(duì)節(jié)點(diǎn)i的影響強(qiáng)度. 當(dāng)aij=0 時(shí),表示節(jié)點(diǎn)j和節(jié)點(diǎn)i之間不存在有向邊 (xj→xi) ;當(dāng)時(shí),aij的值越大, 表示節(jié)點(diǎn)j對(duì)節(jié)點(diǎn)i的影響強(qiáng)度越大.

對(duì)于有向網(wǎng)絡(luò)G(A) , 將網(wǎng)絡(luò)中所有邊的方向翻轉(zhuǎn)后形成的新網(wǎng)絡(luò)記為G(AT) , 稱G(AT) 為原網(wǎng)絡(luò)G(A) 的轉(zhuǎn)置網(wǎng)絡(luò), 原網(wǎng)絡(luò)G(A) 中的邊(xi→xj) 和轉(zhuǎn)置網(wǎng)絡(luò)中的邊 (xj→xi) 互為轉(zhuǎn)置邊.如圖1(a) 所示的網(wǎng)絡(luò), 當(dāng)其所有邊的方向翻轉(zhuǎn)之后, 形成的轉(zhuǎn)置網(wǎng)絡(luò)如圖1(b)所示. 網(wǎng)絡(luò)中一共存在7 對(duì)轉(zhuǎn)置邊, 分別是邊 (x4→x1) 和邊 (x1→x4) ,(x4→x3) 和邊 (x3→x4) , (x4→x5) 和邊 (x5→x4) ,(x4→x6) 和邊 (x6→x4) , (x1→x2) 和邊 (x2→x1) ,(x3→x2) 和邊 (x2→x3) , (x6→x5) 和邊 (x5→x6).

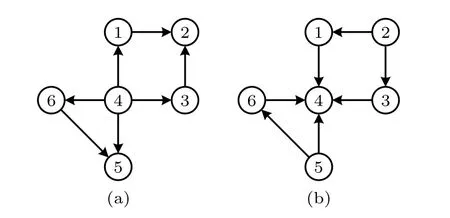
圖1 原網(wǎng)絡(luò)與轉(zhuǎn)置網(wǎng)絡(luò) (a) 原網(wǎng)絡(luò); (b) 轉(zhuǎn)置網(wǎng)絡(luò)Fig. 1. Original network and transpose network: (a) Originalnetwork; (b) transpose network.

有向網(wǎng)絡(luò)G(A) 邊集的一個(gè)子集合中任意兩條邊沒(méi)有公共的始點(diǎn)也沒(méi)有公共的終點(diǎn), 稱這個(gè)子集為網(wǎng)絡(luò)G(A) 的一個(gè)匹配集. 如果一個(gè)節(jié)點(diǎn)是匹配集中某條邊的終點(diǎn), 稱該節(jié)點(diǎn)為匹配節(jié)點(diǎn), 否則該節(jié)點(diǎn)為未匹配節(jié)點(diǎn). 網(wǎng)絡(luò)G(A) 的匹配集中所含邊數(shù)最多的匹配集被稱為最大匹配. 如果一個(gè)網(wǎng)絡(luò)的某個(gè)匹配中, 所有的頂點(diǎn)都是匹配節(jié)點(diǎn), 稱該匹配為一個(gè)完美匹配.

對(duì)一個(gè)有向網(wǎng)絡(luò)G(A) 而言, 它可能存在多組不同的最大匹配. 有向網(wǎng)絡(luò)的最大匹配可以通過(guò)對(duì)應(yīng)的二部圖得到, 具體做法通過(guò)以下方式構(gòu)造:

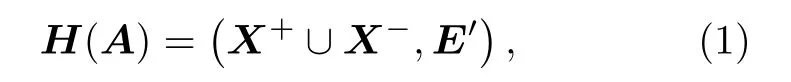
2.2 有向網(wǎng)絡(luò)系統(tǒng)動(dòng)力學(xué)方程

線性時(shí)不變系統(tǒng)動(dòng)力學(xué)方程可以表示為

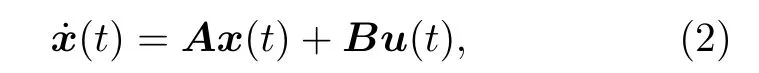
其中,x(t)=(x1(t),x2(t),···,xN(t))T為狀態(tài)向量,A∈RN×N為狀態(tài)矩陣,B∈RN×M稱為輸入矩陣,u(t)=(u1(t),u2(t),···,uM(t))T為輸入向量.

將線性時(shí)不變系統(tǒng)(LTI)引入到有向網(wǎng)絡(luò)中,得到有向網(wǎng)絡(luò)系統(tǒng)G(A,B)=(XA∪XB,EA∪EB) ,其中XA={x1,x2,···,xN},XB={u1,u2,···,uM},aij表示節(jié)點(diǎn)j對(duì)節(jié)點(diǎn)i的影響強(qiáng)度,aij的值越大, 影響強(qiáng)度越大.EB=bij表示在t時(shí)刻將輸入信號(hào)uj(t) 作用于節(jié)點(diǎn)i.

2.3 結(jié)構(gòu)能控性

對(duì)于一個(gè)線性時(shí)不變系統(tǒng), 若存在一個(gè)分段連續(xù)的輸入u(t) , 能夠在有限時(shí)間 [t0,tf] 內(nèi)使得系統(tǒng)從任意初始狀態(tài)x(t0) 轉(zhuǎn)移到任意終止?fàn)顟B(tài)x(tf) , 則稱此系統(tǒng)是狀態(tài)能控的. 在控制理論中, Kalman[32]提出的能控性判據(jù)為判斷系統(tǒng)能控性提供了代數(shù)方法, 即系統(tǒng)完全能控的充分必要條件是矩陣

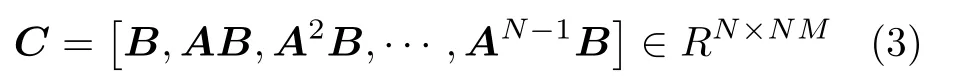
為滿秩, 即 r ank(C)=N, 其中C被稱為能控性矩陣.

在實(shí)際中, 有些網(wǎng)絡(luò)邊權(quán)重不可測(cè), 或者隨著時(shí)間的變化而改變, 因此, Lin[5]提出了結(jié)構(gòu)能控性的概念. 在網(wǎng)絡(luò)系統(tǒng)G(A,B) 中 , 矩陣A和矩陣B被認(rèn)為是結(jié)構(gòu)化的, 即它們的元素要么是固定的零, 要么是獨(dú)立的自由參數(shù). 只需要考慮網(wǎng)絡(luò)本身的拓?fù)浣Y(jié)構(gòu), 而不需要考慮網(wǎng)絡(luò)節(jié)點(diǎn)間的真實(shí)權(quán)重. 如果將G(A) 中的自由參數(shù)固定到某一確定值, 使所得到的網(wǎng)絡(luò)系統(tǒng)G(A,B) 在通常意義上( r ank(C)=N)是能控的, 則該網(wǎng)絡(luò)系統(tǒng)G(A,B)是結(jié)構(gòu)能控的.

在輸入矩陣B中, 和輸入節(jié)點(diǎn)連接的狀態(tài)節(jié)點(diǎn)稱為受控節(jié)點(diǎn), 那些不共享輸入節(jié)點(diǎn)的受控節(jié)點(diǎn)稱為驅(qū)動(dòng)節(jié)點(diǎn). 滿足網(wǎng)絡(luò)結(jié)構(gòu)能控所需的最少的驅(qū)動(dòng)節(jié)點(diǎn)的集合就是最小驅(qū)動(dòng)節(jié)點(diǎn)集(minimum driver node set, MDS), MDS可以通過(guò)最小輸入定理[6]求出.

引理1 最小輸入定理完全控制有向網(wǎng)絡(luò)G(A) 所需要的最少輸入節(jié)點(diǎn)數(shù)NI或者最少驅(qū)動(dòng)節(jié)點(diǎn)數(shù)ND取決于網(wǎng)絡(luò)G(A) 的最大匹配, 如果G(A) 存在完美匹配, 則ND等于1并可選擇網(wǎng)絡(luò)中的任一節(jié)點(diǎn)作為驅(qū)動(dòng)節(jié)點(diǎn); 如果G(A) 不存在完美匹配, 則ND等于網(wǎng)絡(luò)中的未匹配節(jié)點(diǎn)數(shù), 并且未匹配的節(jié)點(diǎn)就是所尋找的驅(qū)動(dòng)節(jié)點(diǎn). 即:

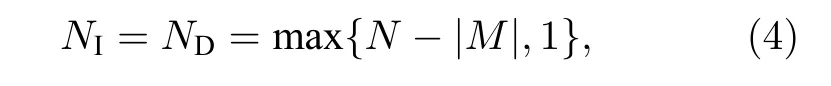
其中M表示網(wǎng)絡(luò)G(A) 的一個(gè)最大匹配,|M|表示網(wǎng)絡(luò)G(A) 最大匹配的邊數(shù).

對(duì)于有向網(wǎng)絡(luò), 某些邊會(huì)因?yàn)橥饨缁蜃陨硪蛩囟? 為了評(píng)判邊失效后對(duì)網(wǎng)絡(luò)能控性的影響,可以由控制節(jié)點(diǎn)密度nD來(lái)量化, 其定義為控制網(wǎng)絡(luò)所需要的最小驅(qū)動(dòng)節(jié)點(diǎn)數(shù)ND占網(wǎng)絡(luò)節(jié)點(diǎn)總數(shù)N的比例, 記為

其中,nD的大小反映復(fù)雜網(wǎng)絡(luò)控制的難易程度, 其值越小, 說(shuō)明網(wǎng)絡(luò)達(dá)到完全能控所需的驅(qū)動(dòng)節(jié)點(diǎn)數(shù)占總節(jié)點(diǎn)數(shù)的比例越小, 網(wǎng)絡(luò)越容易控制, 同時(shí)網(wǎng)絡(luò)的能控魯棒性越好.

3 類(lèi)關(guān)鍵邊集對(duì)網(wǎng)絡(luò)能控性的影響

3.1 節(jié)點(diǎn)分類(lèi)與邊分類(lèi)

對(duì)于給定的網(wǎng)絡(luò), 當(dāng)網(wǎng)絡(luò)滿足結(jié)構(gòu)能控時(shí), 所需的最少的驅(qū)動(dòng)節(jié)點(diǎn)的個(gè)數(shù)是固定的. 然而, 一個(gè)網(wǎng)絡(luò)可能存在多組最大匹配, 導(dǎo)致網(wǎng)絡(luò)存在多種MDSs. 根據(jù)每個(gè)節(jié)點(diǎn)參與MDS的程度[18], 將網(wǎng)絡(luò)節(jié)點(diǎn)分成三類(lèi), 定義如下.

定義1如果一個(gè)節(jié)點(diǎn)參與所有的MDSs, 則這個(gè)節(jié)點(diǎn)稱為關(guān)鍵節(jié)點(diǎn); 如果一個(gè)節(jié)點(diǎn)不全參與所有的MDSs, 則這個(gè)節(jié)點(diǎn)稱為間歇節(jié)點(diǎn); 如果一個(gè)節(jié)點(diǎn)不參與任何一個(gè)MDSs, 則這個(gè)節(jié)點(diǎn)稱為冗余節(jié)點(diǎn).

對(duì)于圖1(a)所示的網(wǎng)絡(luò), 所有可能的最大匹配和MDS如圖2(a). 節(jié)點(diǎn)4參與所有MDSs, 因此為關(guān)鍵節(jié)點(diǎn). 節(jié)點(diǎn)1, 3, 6不全參與所有MDSs,因此為間歇節(jié)點(diǎn). 節(jié)點(diǎn)2, 5不參與任何一個(gè)MDSs, 因此為冗余節(jié)點(diǎn), 結(jié)果如圖2(b)所示.

類(lèi)似地, 根據(jù)每條邊參與最大匹配的程度, 將所有邊分成三類(lèi), 定義如下.

定義2如果一條邊參與所有的最大匹配, 則這條邊稱為關(guān)鍵邊; 如果一條邊不全參與所有的最大匹配, 則這條邊稱為間歇邊; 如果一條邊不參與所有的最大匹配, 則這條邊稱為冗余邊.

對(duì)于圖1(a)所示的網(wǎng)絡(luò), 所有可能的最大匹配如圖2(a). 根據(jù)定義2, 對(duì)網(wǎng)絡(luò)中邊進(jìn)行分類(lèi), 結(jié)果見(jiàn)圖2(b). 其中, 邊 (x6→x5) 參與所有的最大匹配, 為關(guān)鍵邊. 邊 (x4→x1) , (x4→x3) , (x4→x6) ,

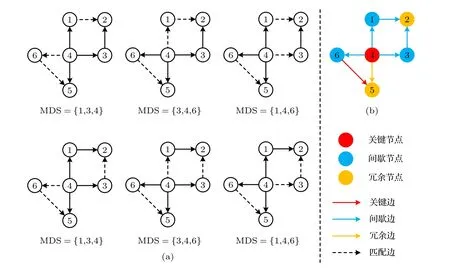
圖2 有向網(wǎng)絡(luò)節(jié)點(diǎn)分類(lèi)和邊分類(lèi) (a) 有向網(wǎng)絡(luò)所有可能的最大匹配以及對(duì)應(yīng)的MDS; (b) 節(jié)點(diǎn)分類(lèi)和邊分類(lèi)Fig. 2. Directed network node classification and edge classification: (a) All possible maximum matching and corresponding MDS of directed network; (b) node classification and edge classification.

(x3→x2) , (x1→x2) 不全參與所有的最大匹配,因此為間歇邊. 邊 (x4→x5) 不參與所有的最大匹配, 因此為冗余邊.

在定義2中, 通過(guò)分析邊在最大匹配中的參與程度, 將網(wǎng)絡(luò)中所有邊分成了三類(lèi), 而最大匹配中邊的個(gè)數(shù)會(huì)直接影響網(wǎng)絡(luò)驅(qū)動(dòng)節(jié)點(diǎn)個(gè)數(shù)ND, 下述定理1討論了三類(lèi)邊失效后對(duì)網(wǎng)絡(luò)能控性的影響.

定理1 網(wǎng)絡(luò)中不同類(lèi)型的邊失效對(duì)能控性的影響

1) 當(dāng)關(guān)鍵邊失效時(shí), 網(wǎng)絡(luò)最大匹配的邊數(shù)減少1, 驅(qū)動(dòng)節(jié)點(diǎn)個(gè)數(shù)ND增加1;

2) 當(dāng)間歇邊失效時(shí), 網(wǎng)絡(luò)最大匹配的邊數(shù)不變, 驅(qū)動(dòng)節(jié)點(diǎn)個(gè)數(shù)ND保持不變, 但是網(wǎng)絡(luò)所有可能的最大匹配個(gè)數(shù)將減少;

3) 當(dāng)冗余邊失效時(shí), 網(wǎng)絡(luò)最大匹配的邊數(shù)不變, 網(wǎng)絡(luò)驅(qū)動(dòng)節(jié)點(diǎn)個(gè)數(shù)ND保持不變, 網(wǎng)絡(luò)所有可能的最大匹配個(gè)數(shù)不變.

證明

1) 反證法: 對(duì)于給定的有向網(wǎng)絡(luò)G(A) , 存在最大匹配M,|M|表示最大匹配中的邊數(shù). i)假設(shè)關(guān)鍵邊失效后, 網(wǎng)絡(luò)最大匹配的邊數(shù)增加t,t＞0.那么在關(guān)鍵邊不失效時(shí), 網(wǎng)絡(luò)最大匹配的邊數(shù)就是|M|+t, 與最大匹配的邊數(shù)唯一矛盾. 因此關(guān)鍵邊失效時(shí), 網(wǎng)絡(luò)最大匹配的邊數(shù)不會(huì)增加. ii)假設(shè)關(guān)鍵邊失效后, 網(wǎng)絡(luò)最大匹配的邊數(shù)保持不變. 那么在關(guān)鍵邊不失效時(shí), 關(guān)鍵邊就不會(huì)一直參與最大匹配, 與關(guān)鍵邊定義矛盾. 因此關(guān)鍵邊失效時(shí), 網(wǎng)絡(luò)最大匹配的邊數(shù)不會(huì)保持不變. iii)假設(shè)關(guān)鍵邊失效后, 網(wǎng)絡(luò)最大匹配的邊數(shù)減少r,r＞1. 當(dāng)關(guān)鍵邊失效后, 假如現(xiàn)在的最大匹配M’ 為原最大匹配M除去關(guān)鍵邊, 則M’ 對(duì)應(yīng)的最大匹配邊數(shù)為|M|-1 ,與假設(shè)的最大匹配的邊數(shù)為|M|-r,r＞1 矛盾.因此關(guān)鍵邊失效時(shí), 網(wǎng)絡(luò)最大匹配的邊數(shù)不會(huì)減少r,r＞1. 綜上i) ii) iii)所述, 當(dāng)關(guān)鍵邊失效時(shí), 網(wǎng)絡(luò)最大匹配的邊數(shù)減少1, 根據(jù)引理1, 驅(qū)動(dòng)節(jié)點(diǎn)個(gè)數(shù)ND增加1.

2) 由于間歇邊不全參與最大匹配, 至少存在一個(gè)最大匹配不包含要失效的間歇邊, 因此間歇邊的失效不影響最大匹配的邊數(shù), 驅(qū)動(dòng)節(jié)點(diǎn)個(gè)數(shù)ND也保持不變. 由于去掉了間歇邊, 也就去掉了所有包含該失效間歇邊的最大匹配, 因此網(wǎng)絡(luò)所有可能的最大匹配個(gè)數(shù)將減少.

3) 由于冗余邊不參與最大匹配, 因此冗余邊去掉之后對(duì)網(wǎng)絡(luò)最大匹配無(wú)影響, 網(wǎng)絡(luò)驅(qū)動(dòng)節(jié)點(diǎn)個(gè)數(shù)ND保持不變, 網(wǎng)絡(luò)所有可能的最大匹配個(gè)數(shù)也不變.

通過(guò)定理1, 將每個(gè)不同類(lèi)型的邊與網(wǎng)絡(luò)能控性(驅(qū)動(dòng)節(jié)點(diǎn)個(gè)數(shù)ND)建立了聯(lián)系.

在對(duì)網(wǎng)絡(luò)中的邊進(jìn)行分類(lèi)時(shí), 根據(jù)定義2, 需要求出網(wǎng)絡(luò)所有的最大匹配, 但這是一個(gè)NP問(wèn)題[33]. 由于給定網(wǎng)絡(luò)的最大匹配邊數(shù)是固定的, 因此, 從最大匹配邊數(shù)變化的角度來(lái)對(duì)邊分類(lèi)將是一個(gè)可行的方法. 根據(jù)定理1可知, 關(guān)鍵邊失效后,會(huì)使網(wǎng)絡(luò)最大匹配邊數(shù)減少1; 冗余邊總是不參與最大匹配, 如果被強(qiáng)制參與匹配(去掉和該邊同出節(jié)點(diǎn)以及同入節(jié)點(diǎn)的所有邊), 會(huì)使原來(lái)參與最大匹配的兩條邊不參與最大匹配, 網(wǎng)絡(luò)中最大匹配邊數(shù)與之前相比將減少1; 如果一條邊既不屬于關(guān)鍵邊又不屬于冗余邊, 則為間歇邊. 綜上三種情況,可以給出網(wǎng)絡(luò)邊分類(lèi)的算法:

算法1 網(wǎng)絡(luò)中邊分類(lèi)算法

Step 1: 求出網(wǎng)絡(luò)一組最大匹配, 記匹配邊數(shù)為m;

Step 2: 遍歷網(wǎng)絡(luò)中所有的邊, 如果存在一條邊 (xi→xj) , 在去掉該邊后, 新網(wǎng)絡(luò)的最大匹配邊數(shù)m1滿足m1=m-1 , 則該邊為關(guān)鍵邊;

Step 3: 遍歷網(wǎng)絡(luò)中所有的邊, 如果存在一條邊 (xi→xj) , 在去掉和該邊同出節(jié)點(diǎn)以及同入節(jié)點(diǎn)的所有邊后, 新網(wǎng)絡(luò)的最大匹配邊數(shù)m2滿足m2=m-1, 則該邊為冗余邊;

Step 4: 遍歷網(wǎng)絡(luò)中所有的邊, 如果存在一條邊 (xi→xj) , 既不屬于關(guān)鍵邊又不屬于冗余邊, 則該邊為間歇邊.

3.2 類(lèi)關(guān)鍵邊集概念

網(wǎng)絡(luò)中某個(gè)或某些邊的失效會(huì)影響網(wǎng)絡(luò)能控性, 使網(wǎng)絡(luò)滿足結(jié)構(gòu)能控所需的最小的驅(qū)動(dòng)節(jié)點(diǎn)個(gè)數(shù)增加, 本文研究了一類(lèi)影響網(wǎng)絡(luò)能控性的邊集稱為“類(lèi)關(guān)鍵邊集”, 其定義如下:

定義3對(duì)于網(wǎng)絡(luò)中的一組邊集EC, 當(dāng)EC同時(shí)失效時(shí)網(wǎng)絡(luò)驅(qū)動(dòng)節(jié)點(diǎn)個(gè)數(shù)(ND)增加1, 并且當(dāng)EC中任意|EC|-1 條邊失效時(shí)網(wǎng)絡(luò)驅(qū)動(dòng)節(jié)點(diǎn)個(gè)數(shù)(ND)保持不變, 則稱邊集EC為類(lèi)關(guān)鍵邊集.

注1|EC|-1 表示邊集EC中的邊數(shù)減1. 根據(jù)定義3可以知道, 對(duì)于存在類(lèi)關(guān)鍵邊集的有向網(wǎng)絡(luò), 移除任意一個(gè)類(lèi)關(guān)鍵邊集, 都會(huì)使ND增加1.

由于類(lèi)關(guān)鍵邊集是一組邊的集合, 不同的類(lèi)關(guān)鍵邊集, 其元素個(gè)數(shù)不一定相同. 因此類(lèi)關(guān)鍵邊集根據(jù)元素的多少, 又可以細(xì)分.

定義4邊數(shù)為1的類(lèi)關(guān)鍵邊集稱為1-元類(lèi)關(guān)鍵邊集. 邊數(shù)為2的類(lèi)關(guān)鍵邊集稱為2-元類(lèi)關(guān)鍵邊集. 同理, 邊數(shù)為x的類(lèi)關(guān)鍵邊集稱為x-元類(lèi)關(guān)鍵邊集.

3.3 類(lèi)關(guān)鍵邊集的辨識(shí)

對(duì)于一個(gè)有向網(wǎng)絡(luò), 通過(guò)定義3, 很難求出網(wǎng)絡(luò)中所有的類(lèi)關(guān)鍵邊集, 因此下面給出類(lèi)關(guān)鍵邊集判定定理.

定理2 類(lèi)關(guān)鍵邊集判定定理

1) 有向網(wǎng)絡(luò)G(A) 中指向同一個(gè)冗余節(jié)點(diǎn)的所有間歇邊的集合, 一定為類(lèi)關(guān)鍵邊集;

2) 有向網(wǎng)絡(luò)G(A) 的轉(zhuǎn)置網(wǎng)絡(luò)G(AT) 中指向同一冗余節(jié)點(diǎn)的所有間歇邊的轉(zhuǎn)置邊的集合, 一定為類(lèi)關(guān)鍵邊集.

證明

1) 根據(jù)冗余節(jié)點(diǎn)的定義, 冗余節(jié)點(diǎn)一定不參與MDSs, 因此冗余節(jié)點(diǎn)一定是匹配節(jié)點(diǎn), 并且指向冗余節(jié)點(diǎn)的邊中一定存在一條匹配邊. 根據(jù)間歇邊的定義, 間歇邊會(huì)參與最大匹配, 因此, 對(duì)于指向同一個(gè)冗余節(jié)點(diǎn)的所有的x條間歇邊, 只有一條參與最大匹配, 而只有把這x條間歇邊全部去掉才可以使網(wǎng)絡(luò)驅(qū)動(dòng)節(jié)點(diǎn)個(gè)數(shù)增加1.

2) 與1)同理, 只有轉(zhuǎn)置網(wǎng)絡(luò)中指向同一個(gè)冗余節(jié)點(diǎn)的所有間歇邊全部去掉之后, 才可以使轉(zhuǎn)置網(wǎng)絡(luò)驅(qū)動(dòng)節(jié)點(diǎn)個(gè)數(shù)增加1, 其對(duì)應(yīng)的原網(wǎng)絡(luò)驅(qū)動(dòng)節(jié)點(diǎn)個(gè)數(shù)也增加1.

注2根據(jù)定義3, 有向網(wǎng)絡(luò)中的關(guān)鍵邊, 一定為類(lèi)關(guān)鍵邊集.

通過(guò)以上分析可以知道, 關(guān)鍵邊是一種特殊的類(lèi)關(guān)鍵邊集, 而類(lèi)關(guān)鍵邊集是關(guān)鍵邊在能控性方面的推廣. 通過(guò)定理2, 可以得到對(duì)應(yīng)的類(lèi)關(guān)鍵邊集搜尋算法.

算法2 類(lèi)關(guān)鍵邊集搜尋算法

Step 1: 對(duì)原網(wǎng)絡(luò)進(jìn)行節(jié)點(diǎn)分類(lèi)和邊分類(lèi), 找出關(guān)鍵節(jié)點(diǎn)、間歇節(jié)點(diǎn)和冗余節(jié)點(diǎn), 關(guān)鍵邊、間歇邊和冗余邊;

Step 2: 記每個(gè)關(guān)鍵邊為1-元類(lèi)關(guān)鍵邊集;

Step 3: 遍歷所有的冗余節(jié)點(diǎn), 將指向同一個(gè)冗余節(jié)點(diǎn)的所有的x條間歇邊記為x-元類(lèi)關(guān)鍵邊集(x=2,3,···);

Step 4: 求原網(wǎng)絡(luò)的轉(zhuǎn)置網(wǎng)絡(luò), 并對(duì)轉(zhuǎn)置網(wǎng)絡(luò)進(jìn)行邊分類(lèi)和節(jié)點(diǎn)分類(lèi), 找出轉(zhuǎn)置網(wǎng)絡(luò)中的關(guān)鍵節(jié)點(diǎn)、間歇節(jié)點(diǎn)和冗余節(jié)點(diǎn), 關(guān)鍵邊、間歇邊和冗余邊;

Step 5: 遍歷轉(zhuǎn)置網(wǎng)絡(luò)中所有的冗余節(jié)點(diǎn), 將指向同一個(gè)冗余節(jié)點(diǎn)的所有的x條間歇邊的轉(zhuǎn)置邊記為x-元類(lèi)關(guān)鍵邊集(x=2,3,···).

對(duì)于圖1(a)所示的網(wǎng)絡(luò), 其原網(wǎng)絡(luò)和轉(zhuǎn)置網(wǎng)絡(luò)的節(jié)點(diǎn)分類(lèi)和邊分類(lèi)如圖3(a)和圖3(b)所示.通過(guò)類(lèi)關(guān)鍵邊集搜尋算法, 網(wǎng)絡(luò)中所有的x-元類(lèi)關(guān)鍵邊集如圖3(c)所示, 在原網(wǎng)絡(luò)中, 邊(x6→x5)為關(guān)鍵邊, 因此為1-元類(lèi)關(guān)鍵邊集. 邊 (x1→x2) ,(x3→x2)為指向冗余節(jié)點(diǎn)2的所有間歇邊, 因此為2-元類(lèi)關(guān)鍵邊集. 在轉(zhuǎn)置網(wǎng)絡(luò)中, 邊 (x1→x4) ,(x3→x4) , (x6→x4) 是指向冗余節(jié)點(diǎn)4的所有間歇邊, 因此其轉(zhuǎn)置邊 (x4→x1) , (x4→x3) ,(x4→x6)為3-元類(lèi)關(guān)鍵邊集.

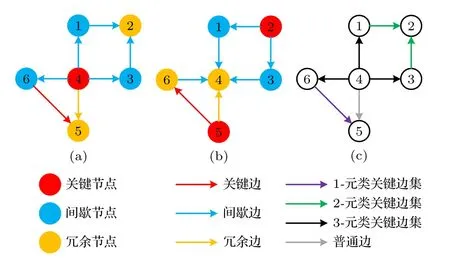
圖3 尋找有向網(wǎng)絡(luò)中的類(lèi)關(guān)鍵邊集 (a), (b) 原網(wǎng)絡(luò)和轉(zhuǎn)置網(wǎng)絡(luò)中的節(jié)點(diǎn)分類(lèi)和邊分類(lèi); (c) 網(wǎng)絡(luò)中的類(lèi)關(guān)鍵邊集Fig. 3. Find the quasi-critical edge set in directed network:(a), (b) Node classification and edge classification in original network and transpose network; (c) quasi-critical edge set in the network.

3.4 類(lèi)關(guān)鍵邊集失效對(duì)能控性影響分析

為了研究類(lèi)關(guān)鍵邊集失效后對(duì)網(wǎng)絡(luò)能控性的影響, 提出了類(lèi)關(guān)鍵邊集失效模型.

類(lèi)關(guān)鍵邊集失效模型

Step 1: 搜尋網(wǎng)絡(luò)中所有的x-元類(lèi)關(guān)鍵邊集(x=1,2,3,···);

Step 2: 任意選擇一個(gè)元素最少的x-元類(lèi)關(guān)鍵邊集(x=1,2,3,···), 將其包含的所有邊在網(wǎng)絡(luò)中移除;

Step 3: 計(jì)算邊移除比例p和新網(wǎng)絡(luò)的能控性nD;

Step 4: 檢查網(wǎng)絡(luò)中是否存在邊. 如果存在邊,轉(zhuǎn)向Step1, 否則結(jié)束運(yùn)行.

由于每次失效都會(huì)選擇一個(gè)類(lèi)關(guān)鍵邊集, 根據(jù)類(lèi)關(guān)鍵邊集的定義, 每移除一個(gè)x-元類(lèi)關(guān)鍵邊集(x=1,2,3,···), 都使網(wǎng)絡(luò)驅(qū)動(dòng)節(jié)點(diǎn)個(gè)數(shù)增加1, 因此網(wǎng)絡(luò)能控性nD與邊移除比例p之間存在正比關(guān)系, 即能控性nD與邊移除比例p的理論關(guān)系曲線為一次分段函數(shù).

假設(shè)在n個(gè)節(jié)點(diǎn),e條邊的有向網(wǎng)絡(luò)中, 最大匹配的邊數(shù)為m(m≤n) 個(gè). 網(wǎng)絡(luò)中所有邊都失效后, 假設(shè)一共移除了c1個(gè)1-元類(lèi)關(guān)鍵邊集,c2個(gè)2-元類(lèi)關(guān)鍵邊集,c3個(gè)3-元類(lèi)關(guān)鍵邊集,···,cj個(gè)j-元類(lèi)關(guān)鍵邊集,···,ci個(gè)i-元類(lèi)關(guān)鍵邊集(m=則能控性nD與邊移除比例p的理論函數(shù)為

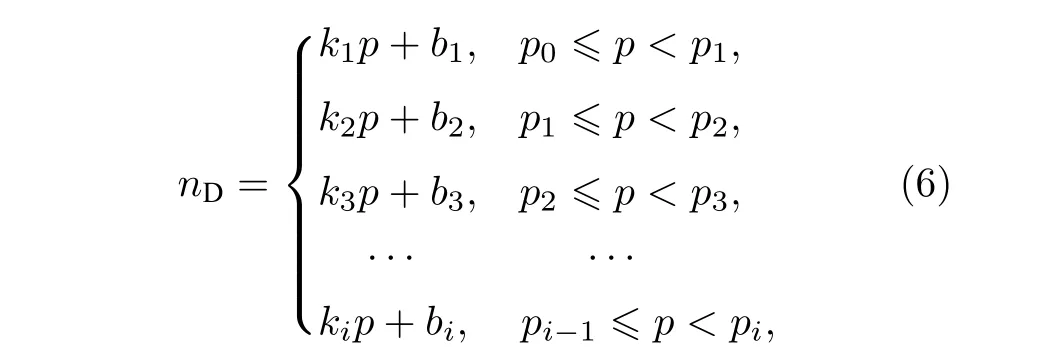
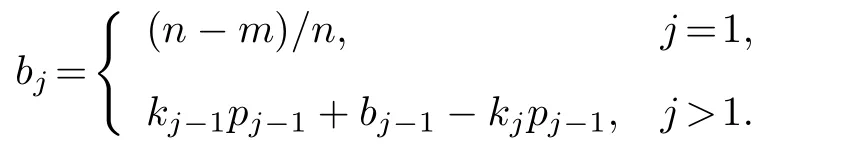
根據(jù)以上分析, 可以畫(huà)出失效函數(shù)的理論曲線, 如圖4所示, 可以更加直觀地看出類(lèi)關(guān)鍵邊集失效后曲線的分段性和一次性. 通過(guò)對(duì)曲線的分析, 可以得到其斜率為

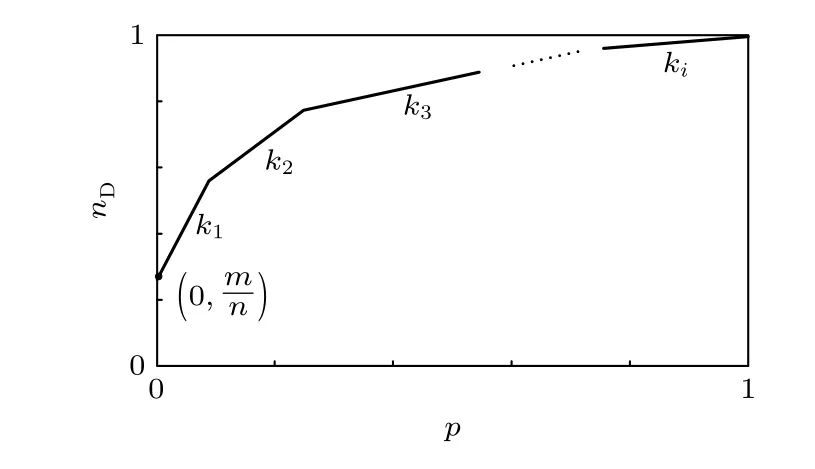
圖4 基于類(lèi)關(guān)鍵邊集的邊失效理論曲線Fig. 4. Theoretical curve of edge failure based on quasi-critical edge set.

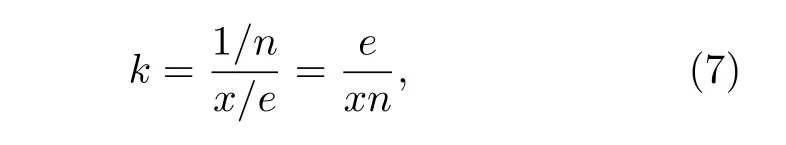
其中,x為每次失效的類(lèi)關(guān)鍵邊集中邊的數(shù)量. 對(duì)于給定的網(wǎng)絡(luò), 斜率的最小值和最大值取決于x的大小. 當(dāng)x=1 時(shí), 即網(wǎng)絡(luò)存在1-元類(lèi)關(guān)鍵邊集, 代入(7)式, 有斜率最大值〈kin〉=〈kout〉, 由于優(yōu)先攻擊邊數(shù)少的類(lèi)關(guān)鍵邊集,因此其初始斜率就是最大斜率, 并且初始斜率的大小與網(wǎng)絡(luò)平均度〈k〉有關(guān). 當(dāng)x→∞時(shí), 代入(7)式, 有最小值由于網(wǎng)絡(luò)的邊數(shù)是有限的, 因此其最小斜率只能無(wú)限趨向于0.

下面通過(guò)一個(gè)實(shí)例介紹類(lèi)關(guān)鍵邊集失效過(guò)程,對(duì)于圖1(a)所示網(wǎng)絡(luò), 其驅(qū)動(dòng)節(jié)點(diǎn)個(gè)數(shù)為3. 按照類(lèi)關(guān)鍵邊集失效模型, 尋找網(wǎng)絡(luò)x-元類(lèi)關(guān)鍵邊集,如圖5(a). 優(yōu)先移除元素個(gè)數(shù)為1的1-元類(lèi)關(guān)鍵邊集 (x6→x5) , 此時(shí)新網(wǎng)絡(luò)驅(qū)動(dòng)節(jié)點(diǎn)數(shù)由3變成4. 重新尋找新網(wǎng)絡(luò)x-元類(lèi)關(guān)鍵邊集, 如圖5(b)所示, 移除2-元類(lèi)關(guān)鍵邊集 (x1→x2) , (x3→x2) , 此時(shí)新網(wǎng)絡(luò)驅(qū)動(dòng)節(jié)點(diǎn)數(shù)由4變成5. 重新尋找新網(wǎng)絡(luò)x-元類(lèi)關(guān)鍵邊集, 如圖5(c)所示, 移除4-元類(lèi)關(guān)鍵邊集 (x4→x1) , (x4→x3) , (x4→x5) , (x4→x6) ,此時(shí)新網(wǎng)絡(luò)節(jié)點(diǎn)全部變成孤立節(jié)點(diǎn), 驅(qū)動(dòng)節(jié)點(diǎn)數(shù)由5變成6, 如圖5(d)所示.

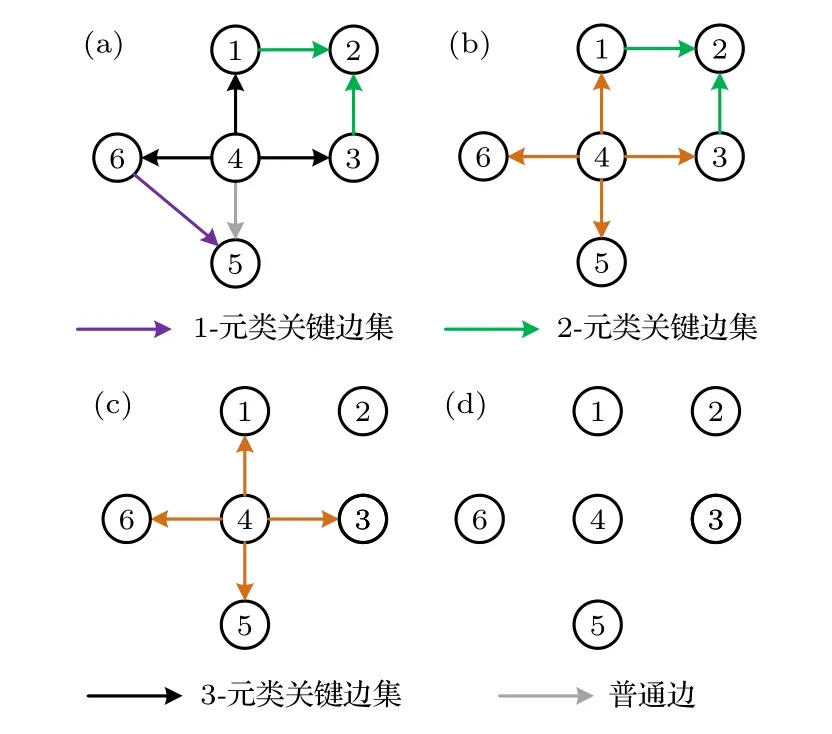
圖5 圖1(a) 所示網(wǎng)絡(luò)的邊失效過(guò)程Fig. 5. The edge failure process of the network shown in Fig. 1(a).

根據(jù)以上失效過(guò)程, 可以計(jì)算出邊失效比例p對(duì)網(wǎng)絡(luò)能控性nD影響的曲線, 與上述攻擊過(guò)程相符, 一共由3段不同斜率、不同截距的一次函數(shù)組成, 如圖6所示, 斜率分別為分析斜率的大小可以知道, 當(dāng)斜率越大時(shí), 說(shuō)明一定數(shù)量的邊失效后, 對(duì)網(wǎng)絡(luò)能控性破壞越大, 網(wǎng)絡(luò)保持能控所需的ND就越多. 當(dāng)斜率越小時(shí), 說(shuō)明一定數(shù)量的邊失效后, 對(duì)網(wǎng)絡(luò)能控性破壞越小, 網(wǎng)絡(luò)保持能控所需的ND就越少.

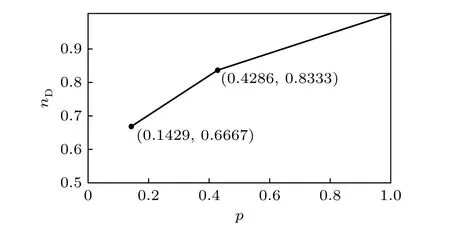
圖6 圖1(a)所示網(wǎng)絡(luò)的邊失效曲線Fig. 6. The edge failure curve of the network shown in Fig. 1(a).

對(duì)于任何有向網(wǎng)絡(luò), 其任意一條邊失效后, 驅(qū)動(dòng)節(jié)點(diǎn)個(gè)數(shù)最多增加1. 當(dāng)關(guān)鍵邊失效時(shí), 會(huì)使網(wǎng)絡(luò)驅(qū)動(dòng)節(jié)點(diǎn)數(shù)增加1, 因此關(guān)鍵邊是對(duì)網(wǎng)絡(luò)能控性影響最大的一類(lèi)邊; 當(dāng)網(wǎng)絡(luò)中無(wú)關(guān)鍵邊時(shí), 失效任意一條邊驅(qū)動(dòng)節(jié)點(diǎn)數(shù)不會(huì)增加, 此時(shí)失效多條邊可導(dǎo)致驅(qū)動(dòng)節(jié)點(diǎn)數(shù)增加,x-元類(lèi)關(guān)鍵邊集 (x≥2) 成為失效后使驅(qū)動(dòng)節(jié)點(diǎn)個(gè)數(shù)增加1的邊數(shù)最少的邊集, 此時(shí)x-元類(lèi)關(guān)鍵邊集是對(duì)網(wǎng)絡(luò)能控性影響最大的邊集. 由于關(guān)鍵邊可作為邊數(shù)為1的類(lèi)關(guān)鍵邊集, 因此在失效相同邊數(shù)的情況下, 類(lèi)關(guān)鍵邊集對(duì)網(wǎng)絡(luò)能控性的影響是最大的. 在某些應(yīng)用背景下,需要保持較高網(wǎng)絡(luò)能控性時(shí), 可對(duì)類(lèi)關(guān)鍵邊集按次序進(jìn)行重點(diǎn)保護(hù).

4 仿真

4.1 網(wǎng)絡(luò)中不同屬性邊占比研究

為了研究3種不同類(lèi)型的邊(關(guān)鍵邊、間歇邊和冗余邊)占網(wǎng)絡(luò)總邊數(shù)的比例p, 分別選取了4種節(jié)點(diǎn)總數(shù)為500的模型網(wǎng)絡(luò)(ER隨機(jī)網(wǎng)絡(luò)[34]、BA無(wú)標(biāo)度網(wǎng)絡(luò)[2]、隨機(jī)三角形網(wǎng)絡(luò)[35,36]和隨機(jī)矩形網(wǎng)絡(luò)[24])進(jìn)行仿真.

對(duì)于ER隨機(jī)網(wǎng)絡(luò), 平均度〈k〉=〈kin〉=〈kout〉從1增加到30, 每次增加1. 對(duì)于BA無(wú)標(biāo)度網(wǎng)絡(luò),新節(jié)點(diǎn)作為弧頭連接的節(jié)點(diǎn)數(shù)min等于新節(jié)點(diǎn)作為弧尾連接的節(jié)點(diǎn)數(shù)mout都從1增加到30, 每次初始網(wǎng)絡(luò)存在min+1 個(gè) 節(jié)點(diǎn)和min+1 條邊, 首尾連接, 保證網(wǎng)絡(luò)的連通性. 對(duì)于隨機(jī)三角形網(wǎng)絡(luò), 平均度從3開(kāi)始, 增加到30, 每次增加1. 對(duì)于隨機(jī)矩形網(wǎng)絡(luò), 平均度從4開(kāi)始, 增加到30, 每次增加1. 對(duì)于每個(gè)確定度下的網(wǎng)絡(luò), 運(yùn)行50次后取平均值, 仿真結(jié)果如圖7所示.

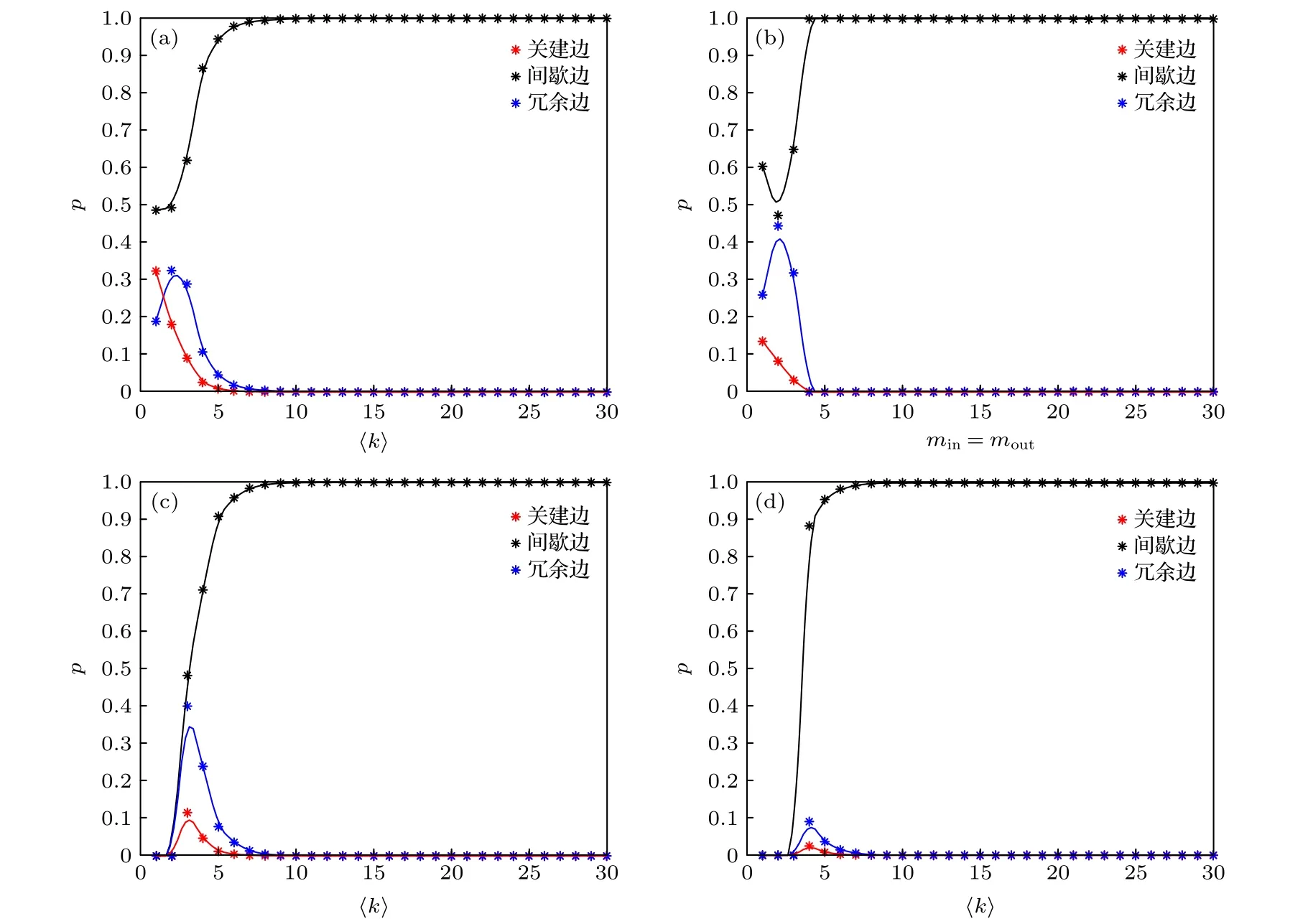
圖7 不同網(wǎng)絡(luò)中關(guān)鍵邊、間歇邊和冗余邊占網(wǎng)絡(luò)總邊數(shù)的比例隨網(wǎng)絡(luò)度的變化曲線 (a) ER隨機(jī)網(wǎng)絡(luò); (b) BA無(wú)標(biāo)度網(wǎng)絡(luò);(c) 隨機(jī)三角形網(wǎng)絡(luò); (d) 隨機(jī)矩形網(wǎng)絡(luò)Fig. 7. Curve of the ratio of critical edge, intermittent edge and redundant edge to the total number of network edges with network degree in different networks: (a) ER random network; (b) BA scale-free network; (c) random triangle network; (d) random rectangle network.

通過(guò)仿真發(fā)現(xiàn)以下結(jié)果. i)隨著網(wǎng)絡(luò)平均度的增加, 網(wǎng)絡(luò)中的關(guān)鍵邊占整個(gè)網(wǎng)絡(luò)總邊數(shù)的比重逐漸降低, 間歇邊占整個(gè)網(wǎng)絡(luò)總邊數(shù)的比重升高. 當(dāng)網(wǎng)絡(luò)中關(guān)鍵邊的數(shù)量幾乎為0, 間歇邊占整個(gè)網(wǎng)絡(luò)邊數(shù)的比重達(dá)到1時(shí), 對(duì)應(yīng)ER隨機(jī)網(wǎng)絡(luò)的平均度〈k〉＞6; BA無(wú)標(biāo)度網(wǎng)絡(luò)新節(jié)點(diǎn)作為弧頭和弧尾連接的節(jié)點(diǎn)數(shù)min=mout＞4 ; 隨機(jī)三角形網(wǎng)絡(luò)的平均度〈 k〉＞7 ; 隨機(jī)矩形網(wǎng)絡(luò)的平均度〈 k〉＞6.ii)隨著網(wǎng)絡(luò)平均度的增加, ER隨機(jī)網(wǎng)絡(luò)和BA無(wú)標(biāo)度網(wǎng)絡(luò)中的冗余邊占整個(gè)網(wǎng)絡(luò)邊數(shù)的比重先增加后降低, 對(duì)于ER隨機(jī)網(wǎng)絡(luò), 其峰值對(duì)應(yīng)平均度〈k〉=2; 對(duì)于BA無(wú)標(biāo)度網(wǎng)絡(luò), 其峰值對(duì)應(yīng)新節(jié)點(diǎn)作為弧頭和弧尾連接的節(jié)點(diǎn)數(shù)min=mout=2.iii)對(duì)于隨機(jī)三角形網(wǎng)絡(luò)和隨機(jī)矩形網(wǎng)絡(luò), 由于其初始度從3和4開(kāi)始, 其冗余邊占整個(gè)網(wǎng)絡(luò)總邊數(shù)的比重隨著網(wǎng)絡(luò)平均度的增加一直減小.

根據(jù)定理1, 網(wǎng)絡(luò)中關(guān)鍵邊的失效會(huì)導(dǎo)致ND增加1, 但是在致密網(wǎng)絡(luò)中, 關(guān)鍵邊的數(shù)量幾乎為0, 只存在間歇邊, 然而單個(gè)間歇邊的失效不會(huì)對(duì)網(wǎng)絡(luò)能控性(ND)造成影響, 因此, 對(duì)于致密網(wǎng)絡(luò)來(lái)說(shuō), 不容易找到影響網(wǎng)絡(luò)能控性的邊. 而本文研究的類(lèi)關(guān)鍵邊集對(duì)能控性的影響結(jié)果適合所有類(lèi)型的網(wǎng)絡(luò). 具體來(lái)說(shuō), 對(duì)于稀疏網(wǎng)絡(luò), 影響網(wǎng)絡(luò)能控性的邊集中既存在1-元類(lèi)關(guān)鍵邊集(關(guān)鍵邊),又存在x-元類(lèi)關(guān)鍵邊集(多條間歇邊組成的集合,x≥2); 對(duì)于致密網(wǎng)絡(luò), 在影響網(wǎng)絡(luò)能控性的邊集中只存在x-元類(lèi)關(guān)鍵邊集(多條間歇邊組成的集合,x≥2 ).

4.2 邊失效對(duì)網(wǎng)絡(luò)能控性影響的對(duì)比

本節(jié)在4種模型網(wǎng)絡(luò)(ER隨機(jī)網(wǎng)絡(luò)、BA無(wú)標(biāo)度網(wǎng)絡(luò)、隨機(jī)三角形網(wǎng)絡(luò)和隨機(jī)矩形網(wǎng)絡(luò))和26種實(shí)際網(wǎng)絡(luò)中, 將類(lèi)關(guān)鍵邊集失效(failure of quasi-critical edge set, FQ)和常見(jiàn)的3種邊失效方式進(jìn)行對(duì)比, 觀察不同失效方式下的網(wǎng)絡(luò)能控性nD, 分析類(lèi)關(guān)鍵邊集失效后對(duì)網(wǎng)絡(luò)能控性的影響.常見(jiàn)的邊失效方式有以下幾種.

1)邊隨機(jī)失效: 隨機(jī)刪除網(wǎng)絡(luò)中的一條邊.

2)基于度的邊失效: 刪除網(wǎng)絡(luò)中度最大的一條邊. 邊度的定義為邊兩端節(jié)點(diǎn)度的幾何均數(shù)[37].對(duì)于邊aij, 其邊度可以表示為其中ki為節(jié)點(diǎn)i的入度,kj為節(jié)點(diǎn)j的出度.

3)基于介數(shù)的邊失效: 刪除網(wǎng)絡(luò)中介數(shù)最大的一條邊. 邊的介數(shù)定義為網(wǎng)絡(luò)中所有的最短路徑中經(jīng)過(guò)邊的數(shù)量比例. 對(duì)于邊aij, 其介數(shù)可以表示為其中Nlm表示節(jié) 點(diǎn)l和節(jié)點(diǎn)m之間的最短路徑的條數(shù),Nlm(aij) 表示節(jié)點(diǎn)l和節(jié)點(diǎn)m之間的最短路徑經(jīng)過(guò)邊aij的條數(shù).

根據(jù)Lu和Li[22]的結(jié)論, 基于重新計(jì)算的失效方式通常比基于初始計(jì)算的失效方式更能損害網(wǎng)絡(luò)的能控性. 因此, 對(duì)于以上3種失效方式, 和本文提出的類(lèi)關(guān)鍵邊集失效模型一樣, 在每次邊失效后都需要對(duì)網(wǎng)絡(luò)中的度或介數(shù)重新計(jì)算. 需要注意的是, 基于隨機(jī)、度、介數(shù)的失效方式每次只攻擊一條邊, 而我們提出的類(lèi)關(guān)鍵邊集失效模型雖然每次移除的邊數(shù)不同, 但由于最終分析的是網(wǎng)絡(luò)邊移除比例p對(duì)網(wǎng)絡(luò)能控性nD的影響, 因此每次移除邊數(shù)的多少對(duì)最終的結(jié)論無(wú)影響.

4.2.1 ER 隨機(jī)網(wǎng)絡(luò)

本節(jié)將生成節(jié)點(diǎn)數(shù)分別為300, 500, 700,〈kin〉=〈kout〉=2的ER隨機(jī)網(wǎng)絡(luò). 考慮到網(wǎng)絡(luò)的能控性與網(wǎng)絡(luò)平均度(邊的密度)具有相關(guān)性[38], 又生成節(jié)點(diǎn)總數(shù)分別為300, 500, 700,〈kin〉=〈kout〉=6的ER隨機(jī)網(wǎng)絡(luò), 按照以上4種邊失效方式(類(lèi)關(guān)鍵邊集失效、隨機(jī)失效、按度失效和按介數(shù)失效)將網(wǎng)絡(luò)中邊移除, 記錄邊失效比例p與網(wǎng)絡(luò)能控性nD的曲線, 如圖8(a)—圖8(f)所示.

圖8 不同節(jié)點(diǎn)總數(shù)和平均度的隨機(jī)網(wǎng)絡(luò)在4種邊失效方式下網(wǎng)絡(luò)能控性 n D 的變化 (a)節(jié)點(diǎn)總數(shù) N =300 , 平均度〈kin〉=〈kout〉=2 的隨機(jī)網(wǎng)絡(luò); (b)節(jié)點(diǎn)總數(shù) N =500 , 平均度〈 kin〉=〈kout〉=2 的隨機(jī)網(wǎng)絡(luò); (c)節(jié)點(diǎn)總數(shù) N =700 , 平均度〈kin〉=〈kout〉=2 的隨機(jī)網(wǎng)絡(luò); (d)節(jié)點(diǎn)總數(shù) N =300 , 平均度〈 kin〉=〈kout〉=6 的隨機(jī)網(wǎng)絡(luò); (e)節(jié)點(diǎn)總數(shù) N =500 , 平均度〈kin〉=〈kout〉=6 的隨機(jī)網(wǎng)絡(luò); (f)節(jié)點(diǎn)總數(shù) N =700 , 平均度〈 kin〉=〈kout〉=6 的隨機(jī)網(wǎng)絡(luò)Fig. 8. The change of controllability n D of random networks with different number of nodes and average degree under four kinds of edge failure modes: (a) A random network with number of nodes N =300 and average degree 〈 kin〉=〈kout〉=2 ; (b) a random network with number of nodes N =500 and average degree 〈 kin〉=〈kout〉=2 ; (c) a random network with number of nodes N=700 and average degree 〈 kin〉=〈kout〉=2 ; (d) a random network with number of nodes N =300 and average degree〈kin〉=〈kout〉=6 ; (e) a random network with number of nodes N =500 and average degree 〈 kin〉=〈kout〉=6 ; (f) a random network with number of nodes N =700 and average degree 〈 kin〉=〈kout〉=6.

通過(guò)仿真發(fā)現(xiàn): i)在不同的4種失效方式下,隨著網(wǎng)絡(luò)邊移除比例p的增加, 網(wǎng)絡(luò)能控性nD也在一直增加, 說(shuō)明網(wǎng)絡(luò)的能控性在不斷降低. ii)不管網(wǎng)絡(luò)節(jié)點(diǎn)總數(shù)N和平均度〈k〉如何變化, 類(lèi)關(guān)鍵邊集失效對(duì)網(wǎng)絡(luò)能控性的影響最大. 在網(wǎng)絡(luò)邊移除前期, 當(dāng)移除比例為0.1時(shí), 網(wǎng)絡(luò)能控性nD上升大約20%. 另外, 按介數(shù)失效和隨機(jī)失效、按度失效相比, 對(duì)網(wǎng)絡(luò)能控性的影響最大, 并且隨著網(wǎng)絡(luò)平均度的增加, 介數(shù)失效和隨機(jī)失效、按度失效之間的差距越來(lái)越明顯. iii)隨著網(wǎng)絡(luò)平均度的增加, 失效曲線的一次性和分段性變得不明顯, 曲線變得更加平滑, 說(shuō)明此時(shí)網(wǎng)絡(luò)中存在單個(gè)類(lèi)關(guān)鍵邊集的元素個(gè)數(shù)非常大.

4.2.2 BA 無(wú)標(biāo)度網(wǎng)絡(luò)

本節(jié)將生成節(jié)點(diǎn)數(shù)分別為300, 500, 700 的BA無(wú)標(biāo)度網(wǎng)絡(luò). 設(shè)置初始網(wǎng)絡(luò)為 4 個(gè)節(jié)點(diǎn)和 4 條邊, 且首尾連接. 為了研究度的影響, 分別使新節(jié)點(diǎn)作為弧頭連接的節(jié)點(diǎn)數(shù)min等于新節(jié)點(diǎn)作為弧尾連接的節(jié)點(diǎn)數(shù)mout等于1或2[39]. 按照以上4種邊失效方式(類(lèi)關(guān)鍵邊集失效、隨機(jī)失效、按度失效和按介數(shù)失效)將網(wǎng)絡(luò)中邊移除, 記錄邊失效比例p與網(wǎng)絡(luò)能控性nD的曲線, 如圖9(a)—圖9(f)所示.

圖9 不同節(jié)點(diǎn)總數(shù)和平均度的無(wú)標(biāo)度網(wǎng)絡(luò)在4種邊失效方式下網(wǎng)絡(luò)能控性 n D 的變化 (a) 節(jié)點(diǎn)總數(shù) N =300 ,min=mout=1 的無(wú)標(biāo)度網(wǎng)絡(luò); (b) 節(jié)點(diǎn)總數(shù) N =500 , m in=mout=1 的無(wú)標(biāo)度網(wǎng)絡(luò); (c) 節(jié)點(diǎn)總數(shù) N =700 ,min=mout=1的無(wú)標(biāo)度網(wǎng)絡(luò); (d) 節(jié)點(diǎn)總數(shù) N =300 , m in=mout=3 的無(wú)標(biāo)度網(wǎng)絡(luò); (e) 節(jié)點(diǎn)總數(shù) N =500 , m in=mout=3 的無(wú)標(biāo)度網(wǎng)絡(luò);(f) 節(jié)點(diǎn)總數(shù) N =700 , m in=mout=3 的無(wú)標(biāo)度網(wǎng)絡(luò)Fig. 9. The change of controllability n D of scale-free networks with different number of nodes and average degree under four kinds of edge failure modes: (a) A scale-free network with number of nodes N =300 and m in=mout=1 ; (b) a scale-free network with number of nodes N =500 and m in=mout=1 ; (c) a scale-free network with number of nodes N =700 and m in=mout=1 ; (d)a scale-free network with number of nodes N =300 and m in=mout=3 ; (e) a scale-free network with number of nodesN=500 and m in=mout=3 ; (f) a scale-free network with number of nodes N =700 and m in=mout=3.

4.2.3 隨機(jī)三角形網(wǎng)絡(luò)

本節(jié)生成節(jié)點(diǎn)總數(shù)分別為300, 500, 700, 平均度為2的隨機(jī)三角形網(wǎng)絡(luò), 又生成節(jié)點(diǎn)總數(shù)分別為300, 500, 700, 平均度為6的隨機(jī)三角形網(wǎng)絡(luò), 選取4種失效方式分別對(duì)網(wǎng)絡(luò)中的邊進(jìn)行移除, 記錄能控性變化nD與邊失效比例p的曲線, 如圖10(a)—圖10(f)所示.

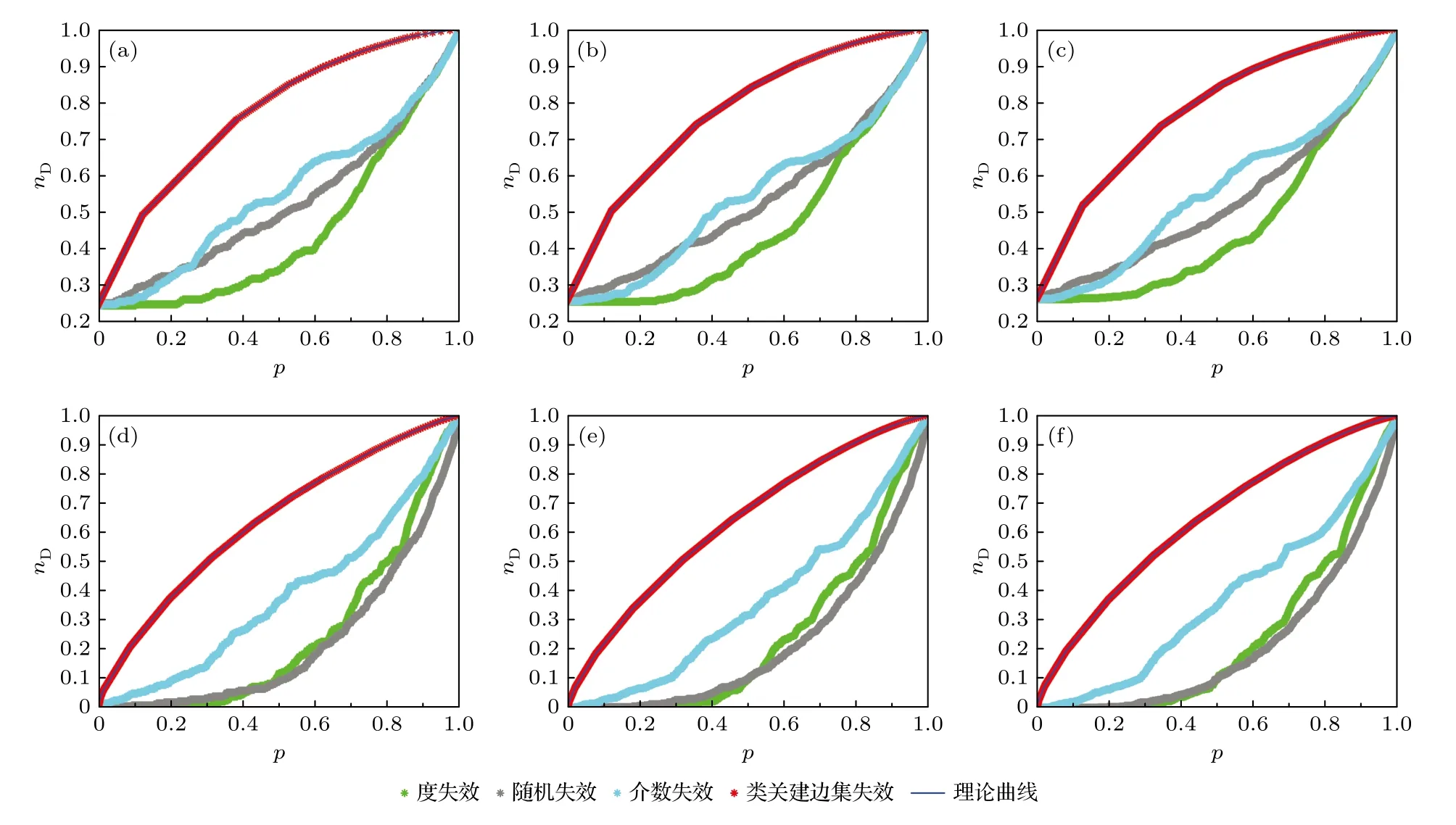
圖10 不同節(jié)點(diǎn)總數(shù)和平均度的隨機(jī)三角形網(wǎng)絡(luò)在4種邊失效方式下網(wǎng)絡(luò)能控性 n D 的變化 (a) 節(jié)點(diǎn)總數(shù) N =300 , 平均度〈kin〉=〈kout〉=2 的隨機(jī)三角形網(wǎng)絡(luò); (b) 節(jié)點(diǎn)總數(shù) N =500 , 平均度〈 kin〉=〈kout〉=2 的隨機(jī)三角形網(wǎng)絡(luò); (c) 節(jié)點(diǎn)總數(shù)N=700 , 平均度〈 kin〉=〈kout〉=2 的隨機(jī)三角形網(wǎng)絡(luò); (d) 節(jié)點(diǎn)總數(shù) N =300 , 平均度〈 kin〉=〈kout〉=6 的隨機(jī) 三角形網(wǎng)絡(luò);(e) 節(jié)點(diǎn)總數(shù) N =500 , 平均度〈 kin〉=〈kout〉=6 的隨機(jī)三角形網(wǎng)絡(luò); (f) 節(jié)點(diǎn)總數(shù) N =700 , 平均度〈 kin〉=〈kout〉=6 的隨機(jī)三角形網(wǎng)絡(luò)Fig. 10. The change of controllability n D of random triangle networks with different number of nodes and average degree under four kinds of edge failure modes: (a) A random triangle network with number of nodes N =300 and average degree〈kin〉=〈kout〉=2 ; (b) a random triangle network with number of nodes N =500 and average degree 〈 kin〉=〈kout〉=2 ;(c) a random triangle network with number of nodes N =700 and average degree 〈 kin〉=〈kout〉=2 ; (d) a random triangle network with number of nodes N =300 and average degree 〈 kin〉=〈kout〉=6 ; (e) a random triangle network with number of nodes N=500 and average degree 〈 kin〉=〈kout〉=6 ; (f) a random triangle network with number of nodes N =700 and average degree 〈 kin〉=〈kout〉=6.

通過(guò)仿真發(fā)現(xiàn): i)在不同的4種失效方式下,隨著網(wǎng)絡(luò)邊移除比例p的增加, 網(wǎng)絡(luò)能控性nD也在一直增加, 說(shuō)明網(wǎng)絡(luò)的能控性在不斷降低; ii)不管網(wǎng)絡(luò)節(jié)點(diǎn)總數(shù)N和平均度〈k〉如何變化, 類(lèi)關(guān)鍵邊集失效對(duì)網(wǎng)絡(luò)能控性的影響最大, 在網(wǎng)絡(luò)邊移除前期, 當(dāng)平均度〈kin〉=〈kout〉=3 時(shí), 邊移除比例為0.1, 網(wǎng)絡(luò)能控性nD上升大約25%. 當(dāng)〈kin〉=〈kout〉=6 時(shí), 邊移除比例為0.1, 網(wǎng)絡(luò)能控性nD上升大約20%; iii) 按介數(shù)失效和隨機(jī)失效、按度失效相比, 當(dāng)網(wǎng)絡(luò)平均度〈k〉較小時(shí), 三者差別不大,隨著網(wǎng)絡(luò)平均度〈k〉的增大, 按介數(shù)失效相較于隨機(jī)失效、按度失效, 對(duì)網(wǎng)絡(luò)能控性的影響逐漸明顯.

4.2.4 隨機(jī)矩形網(wǎng)絡(luò)

本節(jié)生成節(jié)點(diǎn)總數(shù)分別為300, 500, 700, 平均度為2的隨機(jī)矩形網(wǎng)絡(luò), 又生成節(jié)點(diǎn)總數(shù)分別為300, 500, 700, 平均度為6的隨機(jī)矩形網(wǎng)絡(luò), 選取4種失效方式分別對(duì)網(wǎng)絡(luò)中的邊進(jìn)行移除記錄能控性變化nD與邊失效比例p的曲線, 如圖11(a)—圖11(f)所示.

圖11 不同節(jié)點(diǎn)總數(shù)和平均度的隨機(jī)矩形網(wǎng)絡(luò)在四4邊失效方式下網(wǎng)絡(luò)能控性 n D 的變化 (a) 節(jié)點(diǎn)總數(shù) N =300 , 平均度〈kin〉=〈kout〉=2 的隨機(jī)矩形網(wǎng)絡(luò); (b) 節(jié)點(diǎn)總數(shù) N =500 , 平均度〈 kin〉=〈kout〉=2 的隨機(jī)矩形網(wǎng)絡(luò); (c) 節(jié)點(diǎn)總數(shù) N =700 , 平均度〈 kin〉=〈kout〉=2 的隨機(jī)矩形形網(wǎng)絡(luò); (d) 節(jié)點(diǎn)總數(shù) N =300 , 平均度〈 kin〉=〈kout〉=6 的隨機(jī)矩形網(wǎng)絡(luò); (e) 節(jié)點(diǎn)總數(shù)N=500 , 平均度〈 kin〉=〈kout〉=6 的隨機(jī)矩形網(wǎng)絡(luò); (f) 節(jié)點(diǎn)總數(shù) N =700 , 平均度〈 kin〉=〈kout〉=6 的隨機(jī)矩形網(wǎng)絡(luò)Fig. 11. The change of controllability n D of random rectangle networks with different number of nodes and average degree under four kinds of edge failure modes: (a) A random rectangle network with number of nodes N =300 and average degree〈kin〉=〈kout〉=2 ; (b) a random rectangle network with number of nodes N =500 and average degree 〈 kin〉=〈kout〉=2 ; (c) a random rectangle network with number of nodes N =700 and average degree 〈 kin〉=〈kout〉=2 ; (d) a random rectangle network with number of nodes N =300 and average degree 〈 kin〉=〈kout〉=6 ; (e) a random rectangle network with number of nodes N=500 and average degree 〈 kin〉=〈kout〉=6 ; (f) a random rectangle network with number of nodes N =700 and average degree 〈 kin〉=〈kout〉=6.

通過(guò)仿真發(fā)現(xiàn): i)在不同的4種失效方式下,隨著網(wǎng)絡(luò)邊移除比例p的增加, 網(wǎng)絡(luò)能控性nD也在一直增加, 說(shuō)明網(wǎng)絡(luò)的能控性在不斷降低; ii)不管網(wǎng)絡(luò)節(jié)點(diǎn)總數(shù)N和平均度〈k〉如何變化, 類(lèi)關(guān)鍵邊集失效對(duì)網(wǎng)絡(luò)能控性的影響最大. 在網(wǎng)絡(luò)邊移除前期, 當(dāng) 〈kin〉=〈kout〉=3 時(shí), 邊移除比例為0.1, 網(wǎng)絡(luò)能控性nD上升大約25%, 當(dāng) 〈kin〉=〈kout〉=6 時(shí),邊移除比例為0.1, 網(wǎng)絡(luò)能控性nD上升大約20%;iii) 按介數(shù)失效和隨機(jī)失效、按度失效相比, 當(dāng)網(wǎng)絡(luò)平均度〈k〉較小時(shí), 三者差別不大, 隨著網(wǎng)絡(luò)平均度〈k〉的增大, 按介數(shù)失效相較于隨機(jī)失效、按度失效, 對(duì)網(wǎng)絡(luò)能控性的影響逐漸明顯; iv)隨機(jī)失效和按度失效相比, 當(dāng)網(wǎng)絡(luò)平均度〈k〉較小時(shí), 隨機(jī)失效對(duì)網(wǎng)絡(luò)影響較大, 隨著網(wǎng)絡(luò)平均度〈k〉的增大, 按度失效對(duì)網(wǎng)絡(luò)能控性影響大.

4.2.5 實(shí)際網(wǎng)絡(luò)

下面將4種邊失效方式應(yīng)用到實(shí)際網(wǎng)絡(luò)中, 進(jìn)一步比較4種失效方式(關(guān)鍵邊集失效、隨機(jī)失效、按度失效和按介數(shù)失效)對(duì)網(wǎng)絡(luò)能控性nD的影響. 選取電力網(wǎng)絡(luò)、動(dòng)物網(wǎng)絡(luò)、人際關(guān)系網(wǎng)絡(luò)和商品貿(mào)易網(wǎng)絡(luò)等不同領(lǐng)域的26種網(wǎng)絡(luò)[40]. 這些網(wǎng)絡(luò)的規(guī)模從幾十個(gè)到幾百個(gè)節(jié)點(diǎn)不等, 既有稀疏網(wǎng)絡(luò)又有致密網(wǎng)絡(luò). 針對(duì)4種失效方式, 分別計(jì)算當(dāng)邊移除比例p=0.2 ,p=0.5 和p=0.8 時(shí)網(wǎng)絡(luò)能控性nD的數(shù)值, 結(jié)果見(jiàn)表1.

對(duì)比表1中同一移除比例下4種失效方式的能控性nD的大小, 可以發(fā)現(xiàn): i)不管是哪種失效方式, 網(wǎng)絡(luò)能控性nD都在不斷增加, 且類(lèi)關(guān)鍵邊集失效方式對(duì)應(yīng)的nD比其余3種邊失效方式都要大;ii)對(duì)于類(lèi)關(guān)鍵邊集失效, 當(dāng)邊移除比例p=0.8 時(shí),以上不同類(lèi)型的所有網(wǎng)絡(luò)的能控性nD都可以達(dá)到80%以上, 且與初始nD和網(wǎng)絡(luò)平均度的大小無(wú)關(guān);iii)對(duì)于節(jié)點(diǎn)總數(shù)少、邊總數(shù)多(平均度大)的網(wǎng)絡(luò),例如Animal Hens, Collaboration in jazz, Joint senate press releases, Children’s network of friendship, Trade goods in different countries和Questionnaire for grade seven students等, 網(wǎng)絡(luò)能控性的初始值nD比較小, 在邊失效初期, 隨機(jī)失效、按介數(shù)失效和按度失效在移除邊數(shù)比較少時(shí)對(duì)網(wǎng)絡(luò)能控性影響較小, 但是, 類(lèi)關(guān)鍵邊集失效對(duì)網(wǎng)絡(luò)能控性nD造成的破壞性較大; iv) 對(duì)于平均度比較大的網(wǎng)絡(luò), 隨機(jī)攻擊對(duì)網(wǎng)絡(luò)能控性的影響最小,當(dāng)網(wǎng)絡(luò)中邊失效比例達(dá)80%時(shí), 能控性nD還未達(dá)到50%, 例如Animal Hens, Collaboration in jazz,Joint senate press releases, corporate law partnership_law firm, Trade goods in different countries_Foods, Trade goods in different countries_Crude materials和 Trade goods in different countries_Diplomacy等, 這與模型網(wǎng)絡(luò)中的結(jié)論一致.

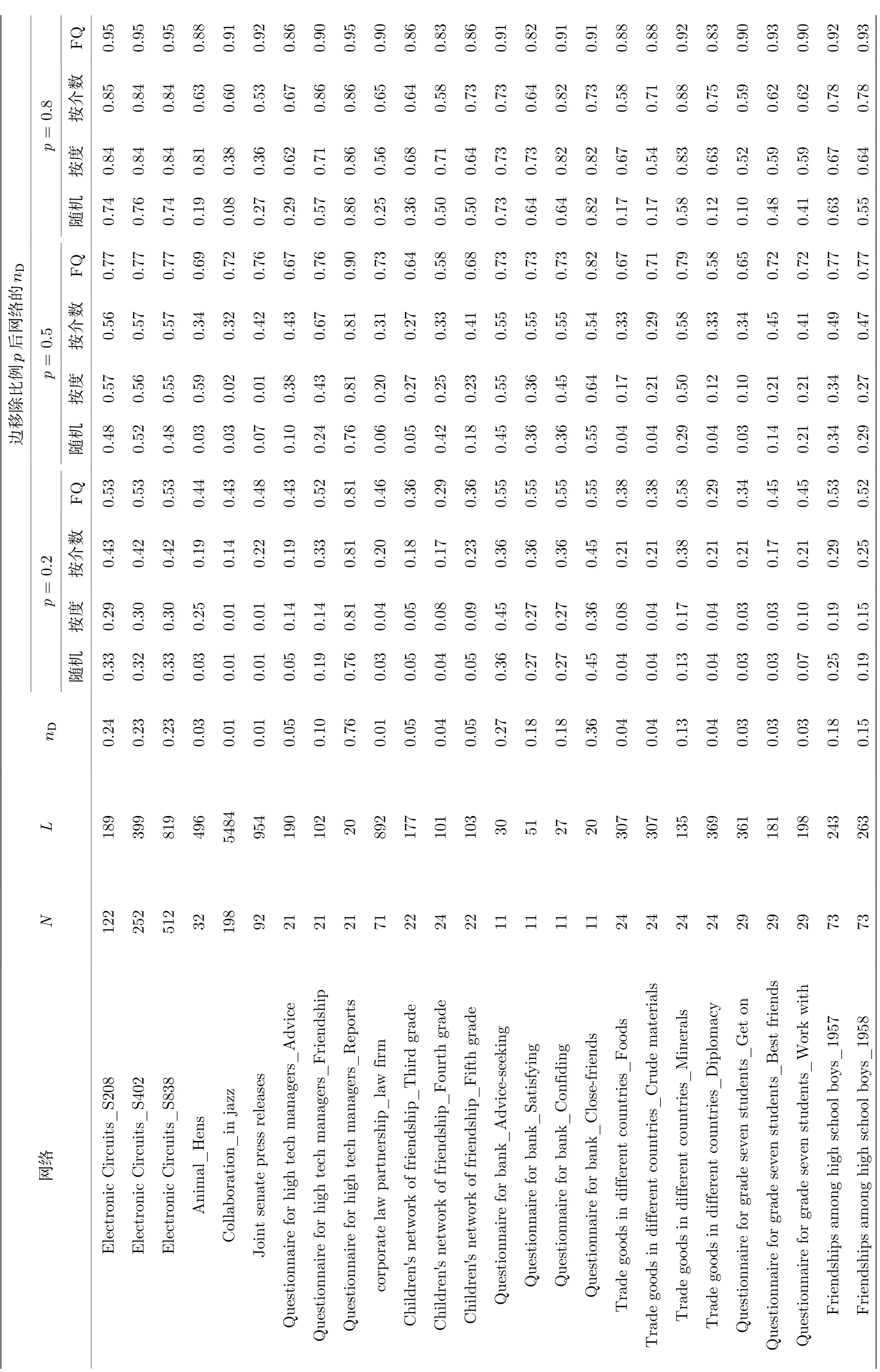
表1 實(shí)際網(wǎng)絡(luò)中4 種邊失效對(duì)能控性的影響Table 1. Influence of four edge failures on controllability in real networks.

5 結(jié) 論

本文通過(guò)對(duì)節(jié)點(diǎn)和邊分類(lèi), 提出了類(lèi)關(guān)鍵邊集的概念, 得到了類(lèi)關(guān)鍵邊集的判定定理, 并提出了基于類(lèi)關(guān)鍵邊集的邊失效模型. 對(duì)類(lèi)關(guān)鍵邊集失效曲線進(jìn)行理論分析, 發(fā)現(xiàn)失效曲線為一次分段函數(shù), 其最大(初始)斜率與網(wǎng)絡(luò)度有關(guān), 并且類(lèi)關(guān)鍵邊集是對(duì)網(wǎng)絡(luò)能控性影響最大的一類(lèi)邊, 和常見(jiàn)的邊失效方式相比, 該失效模型對(duì)網(wǎng)絡(luò)能控性破壞最大. 通過(guò)在4種模型網(wǎng)絡(luò)和26種實(shí)際網(wǎng)絡(luò)中對(duì)比常用的3種邊失效方式(隨機(jī)失效、按度失效和按介數(shù)失效)進(jìn)行仿真, 結(jié)果驗(yàn)證了類(lèi)關(guān)鍵邊集是對(duì)網(wǎng)絡(luò)能控性影響最大的一類(lèi)邊, 以及基于類(lèi)關(guān)鍵邊集的失效模型也是對(duì)網(wǎng)絡(luò)能控性破壞力最大的邊失效方式. 在實(shí)際生活中, 對(duì)于癌細(xì)胞網(wǎng)絡(luò)、恐怖主義通信網(wǎng)絡(luò)等對(duì)人類(lèi)存在危害的網(wǎng)絡(luò), 該失效模型可提供一種可行的攻擊方案.

本文只考慮到有向網(wǎng)絡(luò)一類(lèi)邊在能控性方面的屬性, 有沒(méi)有一類(lèi)節(jié)點(diǎn)也影響網(wǎng)絡(luò)能控性, 或者是否存在一類(lèi)影響網(wǎng)絡(luò)多種性質(zhì)(能控性、連通性等)的節(jié)點(diǎn)或者邊, 需要進(jìn)行深入研究. 另外, 類(lèi)關(guān)鍵邊集的概念只適合有向網(wǎng)絡(luò), 是否可以推廣至無(wú)向網(wǎng)絡(luò)同樣值得去探索. 與此同時(shí), 和攻擊策略對(duì)應(yīng)的就是防御策略, 如何去增強(qiáng)網(wǎng)絡(luò)魯棒性又是另一個(gè)有意義的研究方向.