基于自旋體系的量子機器學習實驗進展*
田宇 林子棟 王翔宇 車良宇 魯大為
(南方科技大學物理系, 深圳 518055)
機器學習因其在模式識別等問題上的優勢已經被廣泛應用到各個研究領域, 然而其運算能力在一定程度上受到經典計算機算力的制約. 近年來, 隨著量子技術的高速發展, 量子計算加速的機器學習在諸多量子體系中進行了初步實驗驗證, 并在某些特定問題上展示出了超越經典算法的優勢. 本文主要介紹兩類典型的自旋體系—核磁共振體系和金剛石氮空位色心體系, 并回顧近年來量子機器學習在這兩類體系上的一些代表性實驗工作.
1 引 言
機器學習是人工智能的重要研究方向之一, 該領域主要采用的方法是對大量數據進行分析, 以識別出數據中包含的信息, 進而提取出數據特征[1].它起源于計算機科學, 在近十年間備受矚目, 在科學技術等諸多領域產生了廣泛的影響[2—4]. 機器學習從基于學習方式上大致可以分為三大類: 監督學習, 無監督學習, 強化學習. 監督學習是通過已有的帶標簽的數據調整數學模型參數, 從而讓模型能夠解決分類或者回歸問題, 監督學習算法包含支持向量機(SVM)、線性回歸、決策樹及神經網絡. 無監督學習則用來對沒有標簽信息的數據進行聚類或者對未標準化的數據進行預處理, 常用的算法有主成分分析(PCA)、詞嵌入及K最近鄰(KNN).強化學習則是通過決策行動得到的環境反饋的獎懲信息作為模型參數的訓練依據, 最終使模型能夠解決規劃決策和模型優化問題, 屬于強化學習的算法有Q-learning、策略梯度算法、SARSA(stateaction-reward-state-action)算法. 上述算法盡管早在20世紀就已經被提出, 但是由于計算機算力的限制以及數據的缺乏, 該領域一直發展緩慢. 直到2012年Hinton教授和他的學生Krizhevsky[5]設計的AlexNet在ImageNet競賽上表現優異, 讓學界及工業界開始關注這種利用大數據和高性能圖形處理器(GPU)訓練的復雜神經網絡模型的價值, 隨后許多優秀的深度學習模型, 如VGGNet[6],ResNet[7], DenseNet[8]的出現標志著深度學習時代的來臨.
盡管現在以深度學習為代表的機器學習算法在計算機視覺、自然語言處理、大數據分析等領域已經有了重大的成就, 但是隨著模型的擴大, 計算機硬件的算力不足及經費開銷已經成為該領域發展的瓶頸. 例如2020年OpenAI公布的目前參數最多的自然語言模型GPT-3[9], 其訓練大致需要512塊V100顯卡訓練4個月, 訓練成本已經高達1200萬美元. 現如今, 經典計算機再次無法滿足機器學習對算力日益增長的需求, 人們迫切地需要發起一場“計算革命”. 量子計算機便是這場革命運動中的排頭兵.
量子計算機中的量子態具備糾纏、疊加等特性, 這些特性是經典計算機所不具備的資源, 可以用來實現對于算法的加速, 稱為量子加速(quantum speedup)[10]. 量子計算機的基礎運算單元為量子比特, 其狀態不似經典比特只有0和1, 而是處在0和1的疊加態上. 因此, 量子比特所包含的信息容量遠遠大于經典比特, 而且量子比特之間可以被糾纏起來, 這些特點使得量子計算機在實現對數據的并行運算處理上具有天然的優勢. 換句話說, 在經典計算機上很難解決或無法解決的問題可能在量子計算機上很容易得到解決[11]. 目前, 量子計算已經能夠實現對某些特定問題的加速運算, 并在實驗上實現了量子計算機發展規劃的第二個里程碑—量子優越性(quantum supremacy). 2019年,Google團隊基于超導體系構建的量子處理器“Sycamore”只用了200 s就完成了經典計算機需要10000年的采樣任務[12]. 2020年, 潘建偉等[13]構建的光量子計算原型機“九章”在處理高斯玻色取樣問題上的計算速率比經典計算機提高了100萬億倍.
量子加速實現的關鍵在于能否找到合適的量子算法[14]. 1985年, Deutsch[15]提出了世界上第一個量子算法, 該算法充分地利用了量子態的疊加特性, 只需要通過一次測量就能夠判斷出目標函數的性質. 1994年, 用于大數分解的Shor算法實現了質因數分解的指數加速[16]. 1995年, 無序搜索的Grover算法實現了對于目標態查找的平方加速[17,18]. 這些重要算法的提出標志著量子計算的研究進入了一個全新的階段. 2009年, Harrow等[19]提出了著名的HHL算法, 該量子算法對于求解線性方程組具有指數加速的作用. 因為機器學習中的數據多以高維矩陣的形式存在, 學習的過程中常伴隨著線性方程組的求解問題, 該算法的提出標志著量子機器學習作為一個重要研究領域的正式建立.
經歷了十多年的發展, 量子機器學習已經在各種實驗體系中得到廣泛應用. 目前, 通用型量子計算機的實現存在著多種技術路線, 例如: 超導電路體系、囚禁離子體系、光學體系, 以及以核磁共振(nuclear magnetic resonance, NMR)和金剛石氮空位(nitrogen vacancy, NV)色心為代表的自旋體系. 自旋體系具有控制精度高、相干時間長等優勢[20], 在量子計算初期階段發展出了許多技術手段, 包括脈沖編譯、最優化控制、動力學解耦等技術[20], 目前也是量子機器學習實驗實現的重要平臺.
本文將簡要介紹核磁共振和金剛石NV色心兩種自旋體系的基本原理, 并梳理近年來國內外各研究組在這兩類平臺上所實現的具有代表性的量子機器學習的工作.
2 核磁共振體系
核磁共振體系是人們研究最早的量子計算體系之一. 早在1938年, Rabi 等[21]發現了著名的Rabi振蕩現象: 位于磁場中的原子核會沿著磁場方向呈正向或反向平行排列, 在施加射頻場之后, 這些原子核的自旋方向則會發生翻轉. 之后, Bloch[22]于1946年發現處于外磁場中的特定核自旋會吸收特定頻率的射頻場能量, 這是人類對于核磁共振現象最早的認識. 經過五十多年的發展, 核磁共振已經在化學、醫療等領域有了諸多應用[23-26], 并且成熟的操控技術使人們可以精確操控核磁共振中耦合起來的兩能級量子系統. 在量子計算概念被提出后, 核磁共振也作為各個量子計算潛在方案中操控比特數最多、操控精度最高的方案而被廣泛研究[20].
核磁共振系統可以用系統哈密頓量和控制哈密頓量聯合進行的動力學演化來描述. 系統哈密頓量給出在靜磁場中單個的, 或者耦合起來的核自旋的能量形式; 而控制哈密頓量來自核自旋共振的控制射頻場.
在核磁共振譜儀中, 樣品被放置在沿著方向的靜磁場B0中. 對于單個自旋為1/2的粒子來說,其在沿著方向的靜磁場B0中的動力學演化被哈密頓量主導:
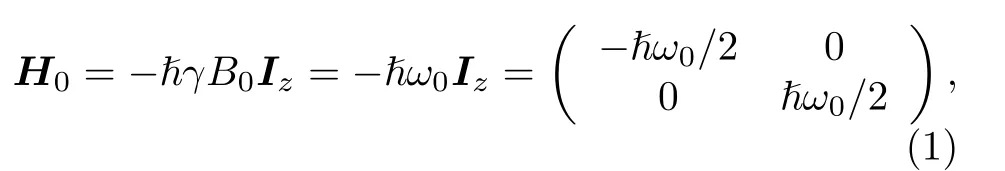
其中, ? 是約化普朗克常數,γ是原子核的旋磁比,ω0/(2π) 是拉莫爾頻率,Iz是沿著方向的核自旋算符. 在核磁共振領域中,Ix,Iy,Iz和泡利算符有著如下對應:
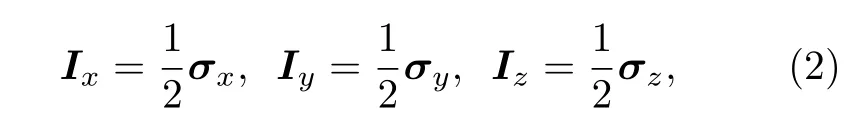
并且
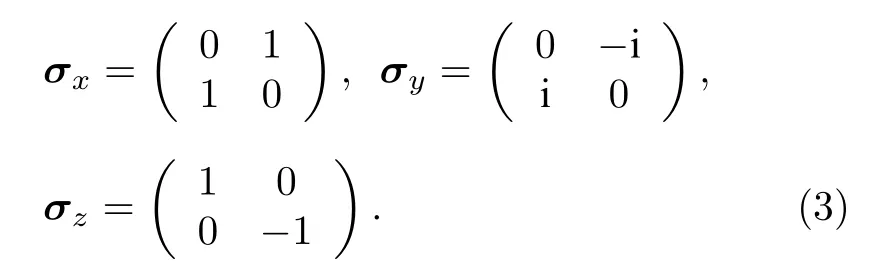
這意味著自旋為1/2的粒子在外磁場中會發生所謂的塞曼效應, 從而產生兩個能級差為 ?ω0的本征態核磁共振量子計算把這兩個本征態作為量子比特的0和1. 當射頻場的能量和能級差匹配時, 核自旋將在兩個本征態之間進行躍遷. 不同種類的核自旋擁有不同的旋磁比γ, 從而擁有不同的拉莫爾進動頻率ω0/(2π). 而相同種類的原子核一般因為周遭不同的電子云排布, 受到不同程度的磁場屏蔽作用(化學位移), 從而也有不同的拉莫爾頻率. 不同的拉莫爾頻率意味著不同的能級差, 于是這些核自旋構成的量子比特可以通過不同的共振頻率來加以區分.
當樣品的分子中有多個核自旋(多量子比特)時, 核自旋之間會產生相互作用. 相互作用的種類有兩種: 直接相互作用(偶極-偶極耦合)和間接相互作用(標量耦合). 在常用的液體核磁共振樣品中, 由核磁矩產生的直接相互作用會因為液體分子的快速滾動而被平均掉. 只剩下由化學鍵產生的間接相互作用, 在弱耦合的情況下2πJij)其哈密頓量的形式為
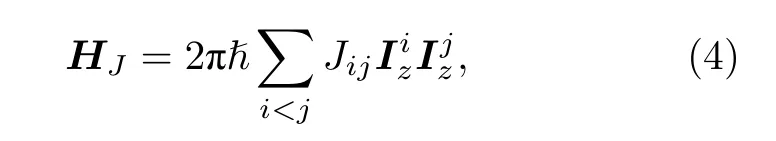
其中Jij為自旋i和自旋j之間的相互作用強度.
所以大多數核磁共振實驗中的系統哈密頓量可表示為核自旋在靜磁場中的哈密頓量和核自旋間兩兩相互作用的哈密頓量之和:
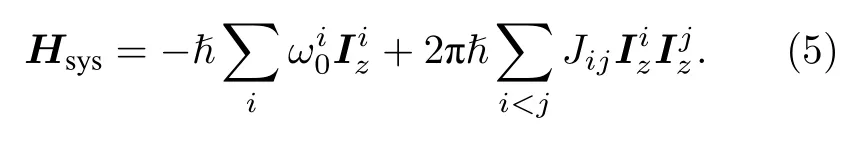
在核磁譜儀中, 控制核自旋躍遷的射頻場在多旋轉坐標系下的哈密頓量可以寫成
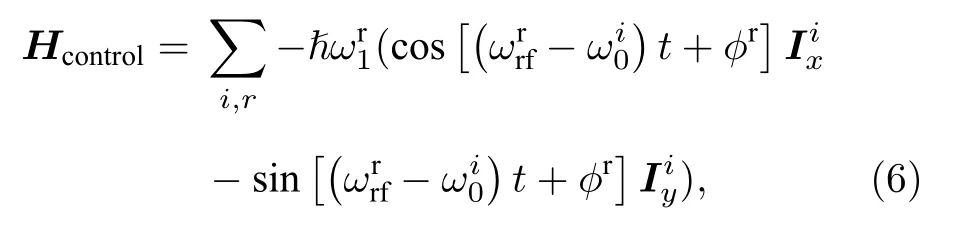
所以核磁共振體系的哈密頓量可以表示為

基于對哈密頓量的控制, 核磁共振系統可以通過贗純態[27,28]的制備實現系統的初始化; 通過調整射頻場參數和核自旋間相互作用時間構建通用邏輯門; 從核磁樣品系綜的自由感應衰減信號中重構出量子態.
從目前的實驗進展來看, 核磁共振量子計算已經非常成熟, 這為那些較為復雜的量子算法提供了一個很好的演示平臺. 目前量子算法在解決線性代數計算問題上已經展現了初步的加速能力, 而例如“傅里葉變換”、“求本征值本征態”、“解線性方程”的問題都是經典機器學習算法中常見的子程序. 接下來, 本文將回顧國內外量子機器學習算法基于核磁共振體系的實驗實現.
2.1 解線性方程組
解線性方程組幾乎是所有科研、工程領域都會面臨的問題, 而經典算法解線性方程組的復雜度限制著計算問題的尺度. 2009年, Harrow等[19]提出了一個能夠在解線性方程組上實現指數加速的HHL量子算法. 它不僅為解線性方程組提供了加速方案, 也是許多量子機器學習算法的基礎. HHL算法的核心是用量子計算機進行矩陣求逆, 從而求解線性方程組. 一個線性方程組可以寫成

其中N×N的參數矩陣可以用它自己的本征值λj和本征態|uj〉 展開向量也可以展開為參數矩陣的逆矩陣可以表示為于是線性方程組的解
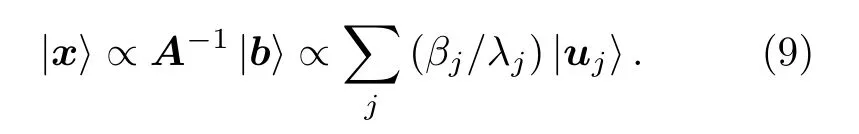
在量子線路中可以通過相位估計算法[29]得到A的本征值λj, 然后對輔助比特旋轉 2 arcsin(C/λj) 角度, 再做一個相位估計的逆過程即可得到
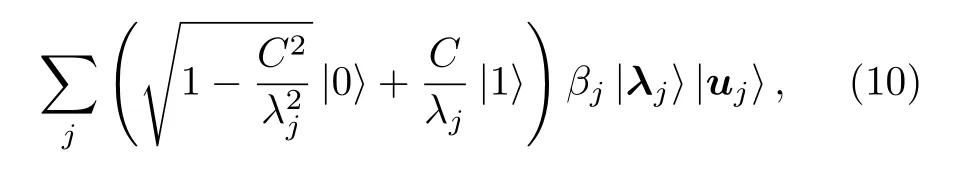
其中C是一個常數. 當輔助比特投影到|1〉 態上時,量子態坍縮為在已知最好的經典算法中需要O(NlogN) 的時間復雜度來求得解向量 |x〉. 上述量子算法只需要的時間復雜度就可以做到同樣的事. 盡管在當前技術下, 量子態制備和量子態讀出在時間復雜度上仍然存在需要解決的難題, HHL算法在解決特定問題上仍有指數加速的潛力.
實驗方面, 光學、核磁共振、超導等量子計算平臺都相繼實現了HHL算法[30—32], 如圖1所示.其中由中國科學技術大學杜江峰團隊完成的工作[31]是在4 bit的核磁共振系統實現了基于量子邏輯門的HHL算法. 算法完成了解 2×2 線性方程組的任務, 并重復對3個不同的向量|b〉 進行驗證(相同的矩陣A). 實驗用氘代氯仿作為樣品, 其中的13C 和3個19F 核自旋作為4個量子比特. 由2 bit組成的寄存器用來實現相位估計算法, 由單比特充當的寄存器用來儲存向量|b〉 , 剩余的1 bit作為輔助比特進行讀出前的投影測量. 對于不同輸入的|b〉 ,4 bit的末態保真度均高于96%. 實驗以優良的準確性驗證了HHL算法的可行性.

圖1 實現HHL算法的量子線路圖. 其中 r =2,t0=2. 單比特門與直線相連的 × 表示SWAP門[31]Fig. 1. The quantum circuit of the HHL algorithm. Parameter r =2,t0=2. Quantum gate The symbol × connected with the straight line represents the SWAP gate[31].
HHL算法及其實驗實現均基于邏輯門模型.受限于當前技術下量子比特的數量, 基于邏輯門的復雜量子算法通常只能在一個很小的維度上進行演示. 而絕熱量子計算(adiabatic quantum computing, AQC)為操控量子系統提供了一種有別于基于邏輯門的方法. 因為量子機器學習通常涉及的多元優化可以直接被AQC實現, 所以對于量子機器學習而言, AQC可能是最有希望取得實際應用的量子模型. AQC的核心是讓系統初態處于一個實驗上容易實現的簡單哈密頓量H0(t) 的基態, 這個哈密頓量會隨著時間緩慢地朝著目標哈密頓量Hp變化, 這個變化過程可以由瞬時哈密頓量表示:
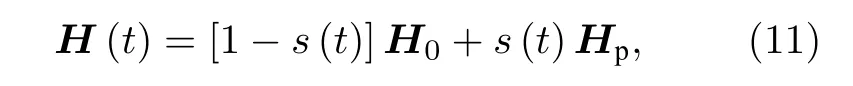
其中s(t) 隨著時間從0變化到1, 導致H(t) 由H0變化至Hp. 絕熱理論告訴我們: 當變化的過程足夠慢, 量子系統將始終待在瞬時哈密頓量H(t) 的基態上. 這樣就通過設計目標哈密頓量來實現目標量子態的獲取.近年, 基于AQC求解線性方程組的量子算法被提出[33]. 清華大學龍桂魯課題組[34]也在2018年在核磁共振系統上實現了兩種基于AQC解8×8線性方程組的算法. 實驗樣品為13C 被標記的巴豆酸分子, 分子上的4個 C 核自旋作為4個量子比特.實驗中第一種算法的絕熱演化的瞬時哈密頓量為
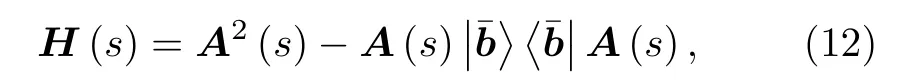
其中A(s)=(1-s)σz?I+sσx?A, 是一個包含了線性方程組系數矩陣的變化參數.|±〉 是σx在計算基矢表示下的本征態,|b〉 則是待解線性方程組右側的向量. 通過對s的構建和緩慢改變, 最終系統的本征態將從|-,b〉 演 化至|+,x〉. 只要將輔助比特舍棄, 即可得到解向量|x〉. 第二種算法的瞬時哈密頓量為
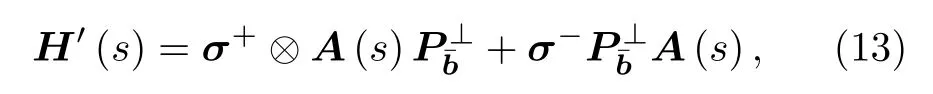
2.2 解線性微分方程
在應用科學面臨的許多動力學問題中, 線性微分方程組(LDEs)扮演了一個很重要的角色. LEDs問題可以概括為: 對于給出的N×N矩陣M,N維的向量 |b〉 以 及初始態向量|x(0)〉 , 希望從含時的微分方程組
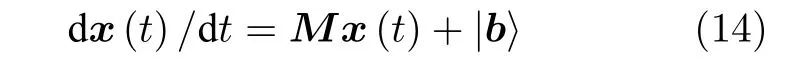
求出解向量|x〉.
和線性方程組問題類似, 經典計算機解線性微分方程要耗費大量計算資源. 當面臨例如量子系統或者流體力學的問題時, 計算的維度大大增加, 這對于經典計算機來說難以解決. 隨著量子計算的發展, 解線性方程組的量子算法已經被提出[19,33], 也相繼在量子計算平臺上進行驗證. 而解線性微分方程組的量子算法雖然也被提出[35—37], 但是這些算法對于目前的量子計算機很難實現. 清華大學龍桂魯團隊[38]提出了一種容易在量子線路中實現的基于邏輯門的解LDEs算法, 并且在4 bit的核磁共振體系上實現了解 4×4 的線性微分方程組,如圖2所示. 線性微分方程組的解向量通式所描述是非幺正演化, 而傳統的量子計算是基于封閉系統和幺正演化. 該算法利用輔助系統使含有非幺正演化子系統的大系統進行幺正演化, 最終得以用便于實驗實現的邏輯門線路完成解微分方程組. 解向量通式可以由計算基矢|j〉 展開,
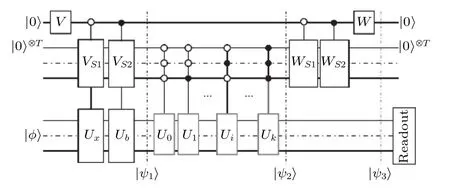
圖2 解線性微分方程的量子線路圖. 線路中第一個輔助寄存器是單比特, 第二個輔助寄存器為 T =log2(k+1) 比特, 然后是一個工作系統. 所有的輔助寄存器被初始化為|0〉|0〉T , 控 制 操 作 U x 和 U b 分別被用來生成 | x(0)〉 和 | b〉.在編碼和解碼期間的演化算子為在線路的結尾, 在所有輔助比特為 | 0〉 的子空間中測量工作系統的態矢[38]Fig. 2. Quantum circuit for solving linear differential equations. The first auxiliary register in the circuit is a single bit, and the second auxiliary register isT=log2(k+1)bits, then is a working system | φ〉. All auxiliary registers are initialized to | 0〉|0〉T , and then the operation U x and Ub are used to generate | x(0)〉 and | b〉. The evolution operator during encoding and decoding is At the end of the circuit, the state vector of the working system is measured in the subspace where all auxiliary bits are | 0〉 [38].
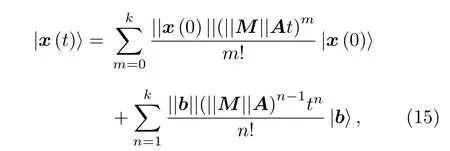
其中x(0) 和b可以由量子態可由算子來描述.
有別于其他以相位估計為核心的量子算法, 該算法的量子加速來自于通過輔助比特將非幺正演化變為幺正演化, 這種做法叫作LCU(linear combination of unitaries)[39]. 對于未來非幺正演化的量子算法研究, 這個工作具有很好的啟發性.
2.3 量子支持向量機
支持向量機(support vector machine, SVM)是一類廣泛使用的通過監督學習實現二元分類的廣義線性分類器, 其在人臉識別、文本分類、手寫字符識別等場景中有重要應用[40]. SVM是通過構造一個線性映射將數據映射到高維特征空間, 在這個高維空間找到一個超平面能使兩類數據的間隔最大, 并通過這個超平面對新的數據進行分類.
已知訓練數據集共有M個訓練樣本, 每個樣本都是一個在N維特征空間的特征向量:
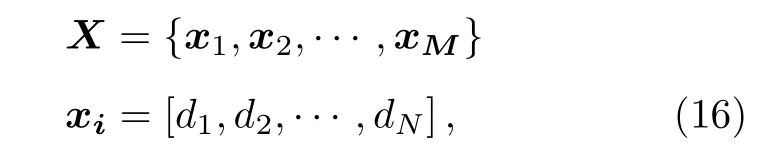
且對應的標簽集為
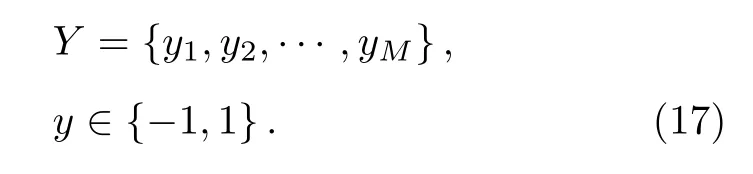
在訓練樣本所在的特征空間中, 通過訓練超平面的法向量w和截距b尋找到一個超平面能夠讓任意數據到這個超平面的距離要大于等于1, 即能夠讓兩類訓練數據分離:
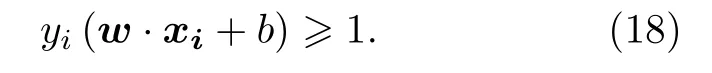
因此判別新數據x類別時, 當w·x+b≥1 時, 認為該數據為+1類, 反之當w·x+b≤-1 , 則認為數據為—1類. 但通常很多數據是無法線性可分的, 因此需要通過一個非線性的函數將數據從低維特征空間映射到更高維度的空間, 同時需要定義該映射函數的內積, 稱為核函數, 以回避復雜的高維顯式內積計算.
SVM在識別階段時間復雜度是O[poly(NM)] ,N是特征空間的維度,M是訓練集的樣本數. 而在訓練階段通常采用二次規劃求解超平面, 而求解二次規劃將涉及M階矩陣的求解,時間復雜度約為O(S3+SN+SNM)和O(NM2)之 間,S為支 持向量個數, 當M數目很大時該矩陣的存儲和計算將耗費大量的計算機內存和運算時間.
為了解決經典SVM無法使用大規模數據進行訓練的難題, 2014年Rebentrost等[41]提出了量子支持向量機(quantum support vector machine,QSVM). QSVM在訓練階段, 將法向量w表示為訓練樣本xi的線性組合,
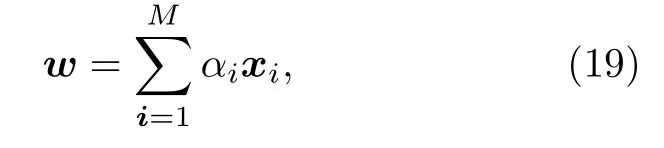
通過最小二乘法, 權重參數α以及截距b可以通過求解線性方程得出:
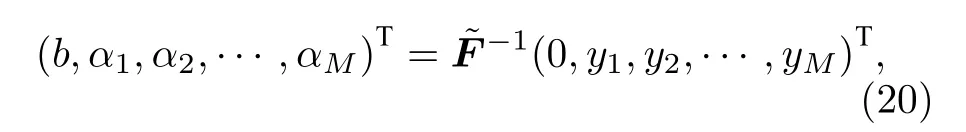
其中是包含核函數K的 (M+1)×(M+1) 的矩陣
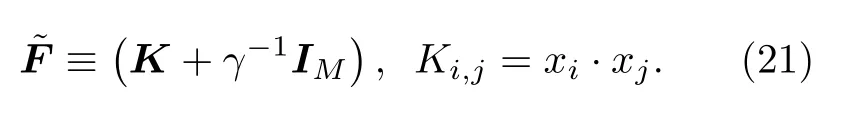
IM是M×M的單位矩陣,γ是設定的訓練誤差與SVM目標的相對權重. 其將SVM訓練轉化為最小二乘法問題再通過HHL算法求解矩陣的逆, 能使QSVM的時間復雜度在訓練和識別階段都能達到O[log(NM)]. 文獻 [42]中杜江峰團隊在NMR系統實現QSVM在手寫數字識別的實驗,采用碘三氟乙烯作為樣品, 其中有一個13C 核自旋和三個19F 核自旋. 兩個比特作為訓練數據寄存器,一個比特作為標簽寄存器, 一個比特作為輔助比特. 實驗巧妙地將字符“6”和“9”編碼成二維線性可分的特征向量用于訓練和測試, 實驗保真度接近99%, 手寫數字識別錯誤率低于4%, 如圖3所示.
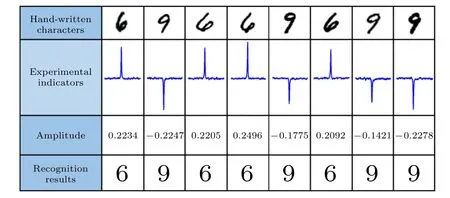
圖3 手寫字符“6”和“9”的識別結果, 第1—4行分別代表手寫字符, 實驗指示符, 相干項的幅度和識別結果[42]Fig. 3. Recognition results of handwritten characters of “6” and “9”. Lines 1 to 4 represent handwritten characters, experimental indicators, amplitude, and recognition results, respectively[42].
2.4 量子主成分分析
主成分分析(principal component analysis,PCA)是機器學習中一種常用且費時的無監督學習算法. 這一方法利用正交變換把由線性相關變量表示的觀測數據轉換為少數幾個由線性無關變量表示的數據, 線性無關的變量稱為主成分. 這個算法主要用于發現數據中的基本結構, 即數據中變量之間的關系[43].
已知數據集一共M個樣本, 每個樣本都是一個在N維特征空間的特征向量:
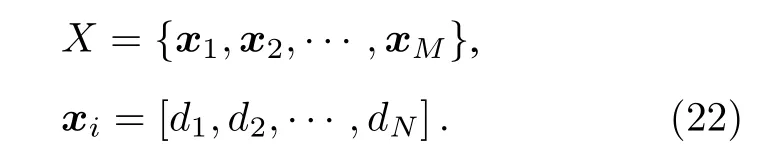
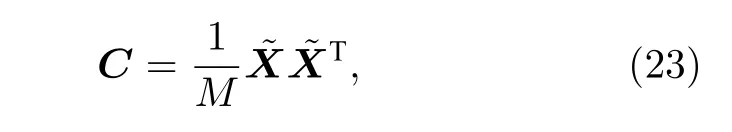
對協方差矩陣C進行特征值分解, 得到所有特征值和對應特征向量, 并對特征向量按其對應特征值大小降序排列, 取前K個特征向量構成投影矩陣P,最終利用投影矩陣P將數據集從N維特征空間投影到K維特征空間. 由此可見特征值分解直接確定了PCA算法的時間復雜度為
2014年, Lloyd等[44]提出了量子主成分分析(quantum principal component analysis, qPCA).qPCA用密度矩陣ρ表示協方差矩陣C, 通過相位估計法將密度矩陣ρ編碼在輔助比特從而解出特征值, 而相位估計法所需的控制門U=e-iρt可以用目標比特和編碼比特之間用時間非常短的SWAP 操作構建:
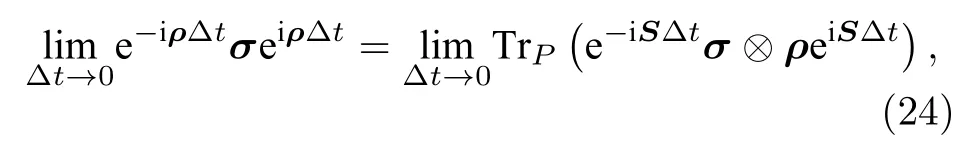
因此qPCA能夠將時間復雜度降低到O(log(N)).
然而上述方法需要的輔助比特數量隨密度矩陣的大小指數增加, 大量的資源消耗以至于在實驗平臺上很難該算法進行驗證, 所以文獻 [45]中實驗團隊通過參數量子電路實現qPCA, 如圖4所示,該方法構建出一個厄密算符U, 能夠將密度矩陣ρ被對角化同時特征值按大小降序排列:
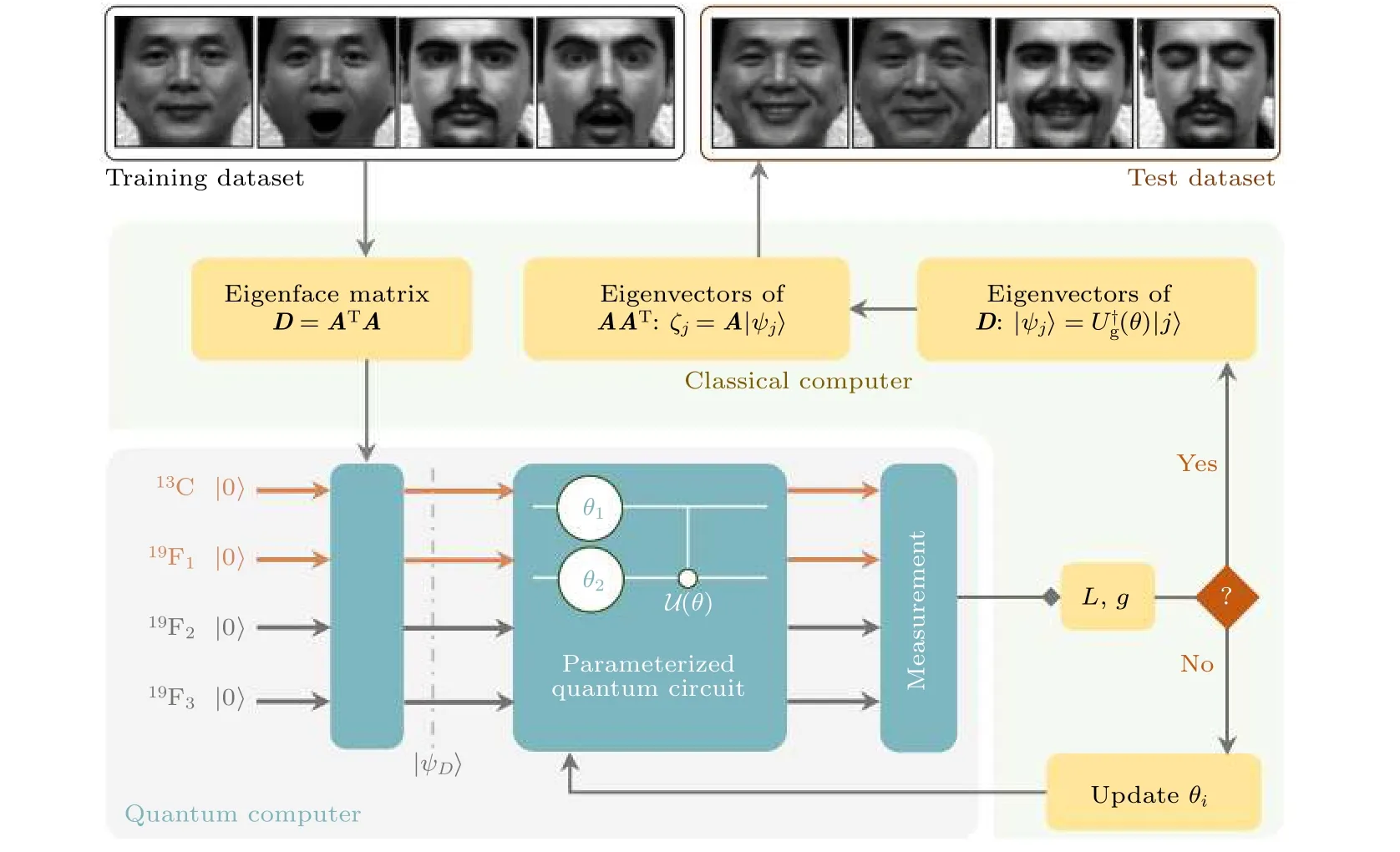
圖4 通過qPCA實現人臉識別的流程圖. 通過混合經典量子控制方法對PQC U (θ) 進行迭代優化, 其中在量子處理器上測量目標函數 L (θ) 和 梯度 g (θ). 參數 θ 的存儲和更新在經典計算機上實現. 用優化后的 U g 來計算特征臉矩陣D和協方差矩陣C的特征向量[45]Fig. 4. Workflow for human face recognition via qPCA. The PQC U (θ) is iteratively optimized via the hybrid classicalquantum control approach, where the objective function L (θ) and the gradient g (θ) are measured on the quantum processor. The storage and update of the parameters θ are implemented on a classical computer. The optimized PQC with the operator U g is applied to compute the eigenvectors of the eigenface matrix D and the covariance matrix C =AAT [45].
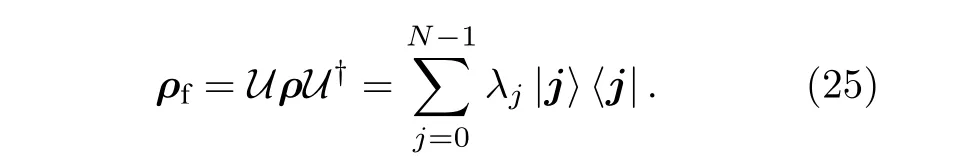
這需要構建一個參數量子電路U(θ) 以及一個算符P:
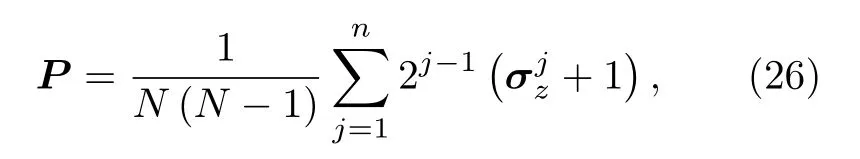
構建出損失函數L(θ) :
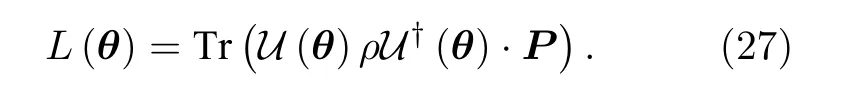
通過梯度下降優化參數θ最小化損失函數L(θ) ,就能訓練出目標厄密算符U, 從而實現qPCA算法. qPCA求解出人臉圖片訓練集協方差矩陣的特征值和對應的特征向量, 通過特征向量構造投影矩陣將高維的圖片數據投影到低維空間, 再通過歐拉距離公式將測試集圖片分類實現人臉識別. 實驗使用四比特核磁共振量子系統, 將量子比特編碼在核自旋, 通過選擇躍遷法初始化量子系統, 并用梯度下降優化控制脈沖方法來載入經典數據, 最后利用量子計算機和經典計算機混合系統優化參數量子電路. 實驗最終求出的特征值保真度達到99%, 測試集人臉識別正確率為100%.
3 NV色心體系
金剛石中的NV色心由一個替代C原子的N原子以及相鄰位置C原子的缺失產生的空位組成[46], 如圖5(a)所示. NV色心是一種很重要的量子體系, 得益于其固態及室溫下可操控等特點, 在量子計算、量子信息、量子精密測量等多個領域都有很好的應用前景[47-49]. 目前, 國內外都有科研團隊在基于NV色心體系的量子技術上展開研究. 自然狀態下, NV色心具有兩種電荷態-電中性和帶負電荷. 帶負電的NV—由于其便于初始化、操控、讀出, 對其本身及其應用的研究也最為廣泛和深入,本章節中我們將要回顧的相關研究也均是基于NV—.
對于NV—, 色心在俘獲一個電子后帶負電.N原子與相鄰的C原子形成共價鍵, 與空位之間不成鍵, 所以貢獻兩個電子, 同樣, 空位周圍的3個C原子也分別貢獻1個電子, 本身的5個電子, 加上俘獲的電子, 共有6個電子. 在實驗中可以認為其等價于1個自旋為1的電子自旋. NV—的基態和激發態的電子態分別為3A2和3E, 均為自旋三重態, 基態因自旋之間的相互作用分裂成|ms=0〉 和|ms=±1〉 , 而|ms=±1〉 是簡并的[50], 如圖5(b)所示. 選取其中的兩個能級, 就可以構建一個量子比特. 除電子自旋外, 形成色心的14N (15N )原子也可以作為一個自旋為1(1/2)的核自旋量子比特, 若在色心周圍存在13C 原子, 同樣可以作為自旋為1/2的量子比特, 這是目前基于NV色心實驗體系來擴展量子比特的主要手段.
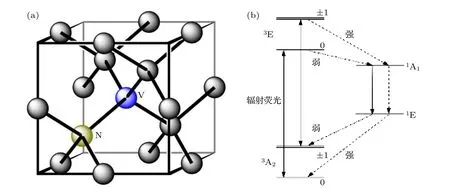
圖5 (a)金剛石NV色心結構圖; (b) NV色心電子能級躍遷過程示意圖, 3 A2 和 3 E 分別代表基態和激發態, 1 A1 和 1 E 為中間亞穩態, 從激發態直接躍遷回基態會發出熒光, 而經中間態回基態不會發出熒光Fig. 5. (a) NV color center structure; (b) schematic diagram of the transition process of NV color center electron energy level,3A2 and 3 E represent the ground state and excited state, respectively, 1 A1 and 1 E are the intermediate metastable states, which from the excited state directly transitions back to the ground state and emit fluorescence. But the path througt metastable state returns to the ground state without emitting fluorescence.
在不外加靜磁場的情況下, 由于自旋之間的相互作用, 劈裂成|ms=0〉 和|ms=±1〉 , 其零場劈裂為2.87 GHz. 施加靜磁場后, 簡并的能級|ms=±1〉將會分開, 并且劈裂會隨著軸向磁場的增強而增大.
在外場下NV色心的系統哈密頓量(以電子自旋與14N 核自旋的兩比特系統為例):
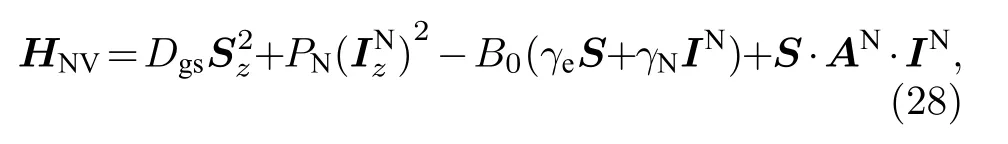
其中,與分別為NV電子自旋與14N 核自旋算符,Dgs= 2.87 GHz, 為NV的電子自旋零場劈裂,PN= —4.95 MHz[51]為NV中心14N 核自旋的四偶極矩劈裂. (28)式中的第三項為NV在外磁場下的塞曼劈裂, 其中γe= 2.082 MHz/G與γN=—0.308 kHz/G分別為NV電子自旋與14N 核自旋的旋磁比. 最后一項是NV電子自旋與14N 核自旋的超精細相互作用(hyperfine interaction),AN為超精細結構張量.
要進行量子計算, 量子體系不僅要具備可操控的量子比特, 還要能夠初始化以及讀出其狀態. 對于NV色心, 其電子自旋是通過激光實現初始化和讀出的. NV—的零聲子線位于637 nm, 在室溫下,由于聲子的參與, 一般使用532 nm的激光激發其至激發態. 當處于激發態時, 有兩種路徑可以回到基態. 第一種是輻射637—750 nm的熒光由激發態直接躍遷回基態, 第二種則是經過中間態回到基態. 對于第二種情況, 自旋是不守恒的, 且不會輻射637—750 nm的熒光[52]. 值得注意的是, 如果NV色心的電子在激發前處于|ms=±1〉 自旋態, 被激發到第一激發態之后, 其將更傾向于通過中間態回到基態, 這就意味著將會有更大的概率得到|ms=0〉的自旋態. 同時, 如果NV色心的電子在基態時處于|ms=0〉 的自旋態, 它會有更大的概率沿著輻射躍遷的路徑, 釋放熒光后直接回到基態[53].所以我們還是有更大的概率得到|ms=0〉 的自旋態. 經過這個過程, 電子在|ms=±1〉 上的布居度將不斷減少,|ms=0〉 上的布居度將不斷的增大[46].由此, 可以實現對色心電子自旋的初始化. 同樣讀出時也會用到上面的性質. 經過中間態回到基態的躍遷過程并不會輻射637—750 nm的熒光, 所以通過熒光強度可以判斷出電子自旋躍遷回基態時經歷的路徑. 同時結合所知的, 處于不同自旋態的電子自旋躍遷時選擇路徑的傾向也不同, 可以得出結論: NV色心在不同自旋態時, 對應的輻射熒光強度的不同, 以此區分色心的自旋態.
NV色心體系由于其比較成熟的操控技術、較長的退相干時間(NV基態自旋具有固體中任何電子自旋中最長的室溫單自旋退相干時間(T2), 在某些樣品中大于1.8 ms), 成為了很多科研組在實驗體系下實現量子算法的選擇. 將NV色心體系作為量子模擬器進行模擬以幫助解決物理問題也是近年來的一個重要研究方向.
3.1 卷積神經網絡
拓撲相的發現改變了人們對量子相的理解. 不像傳統的相位, 拓撲相位不滿足對稱破裂的范式.相反, 每個對稱類中都存在不同的拓撲相. 在實驗中, 拓撲相的識別通常依賴于測量具有拓撲起源的某些屬性, 而在實驗上實現一個明確可以辨別拓撲相的方法, 是十分具有挑戰性的. 機器學習很有希望幫助解決這一問題. 在鄧東靈與段路明課題組合作的工作[54]中, 利用機器學習對三維手性拓撲絕緣體的外來拓撲相進行了識別.
卷積神經網絡(convolutional neural networks,CNN)作為如今發展最迅速的一種神經網絡模型,在計算機視覺、醫學影像處理、自然語言處理等領域廣泛使用[55,56], 該模型的共享權值的特點, 大大減少了模型訓練的復雜度, 同時能夠進行表征學習, 并且提取出數據的全局特征和局部特征.
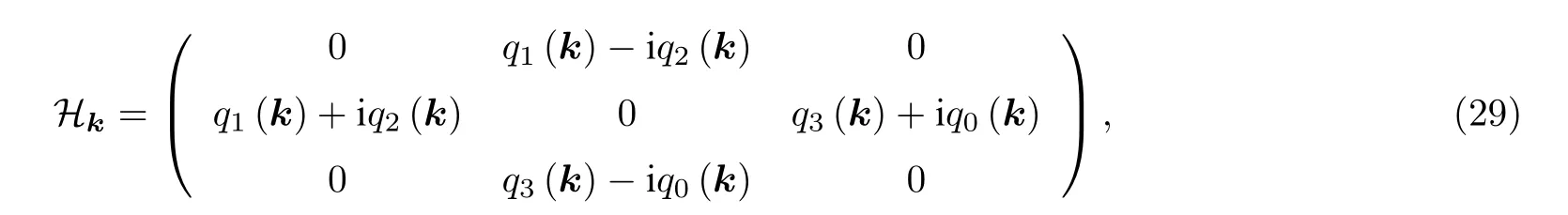
其中q1(k)=tsinkx,q2(k)=tsinky,q3(k)=tsinkz,q0(k)=t(coskx+cosky+coskz+h).t被設定為1, 而h是一個與維度無關的可調參量. 通過調控NV色心電子自旋基態的三個能級, 在實驗上成功模擬出了所需的哈密頓量, 如圖6(a)所示. 通過將NV色心基態的三個能級編碼為|1〉,|0〉,|-1〉 態,觀察Hk可以發現其并沒有對角項, 并且|1〉 與|-1〉之間并沒有直接的耦合. 因此實驗中可以施加能級之間的共振微波, 通過絕熱過程, 可以實現對應不同k值點的哈密頓量.
利用NV色心中的電子自旋模擬的三維手性拓撲絕緣體哈密頓量生成的原始數據, 訓練卷積神經網絡以識別拓撲相, 這樣的監督學習類似于處理經典的圖像識別. 如圖6(b)所示,將在10 ×10 × 10規則網格的密度矩陣的實驗數據作為輸入, 通過一個用來預測拓撲不變量的預訓練卷積神經網絡遷移到分類不同拓撲相的問題中, 輸出各個可能的拓撲相得經典概率. 實驗發現即使只用輸入10%實驗數據, 模型也能夠達到90%的識別率, 表明了即使使用最少數量的數據樣本,也可以訓練CNN來成功識別拓撲階段, 如圖7所示.
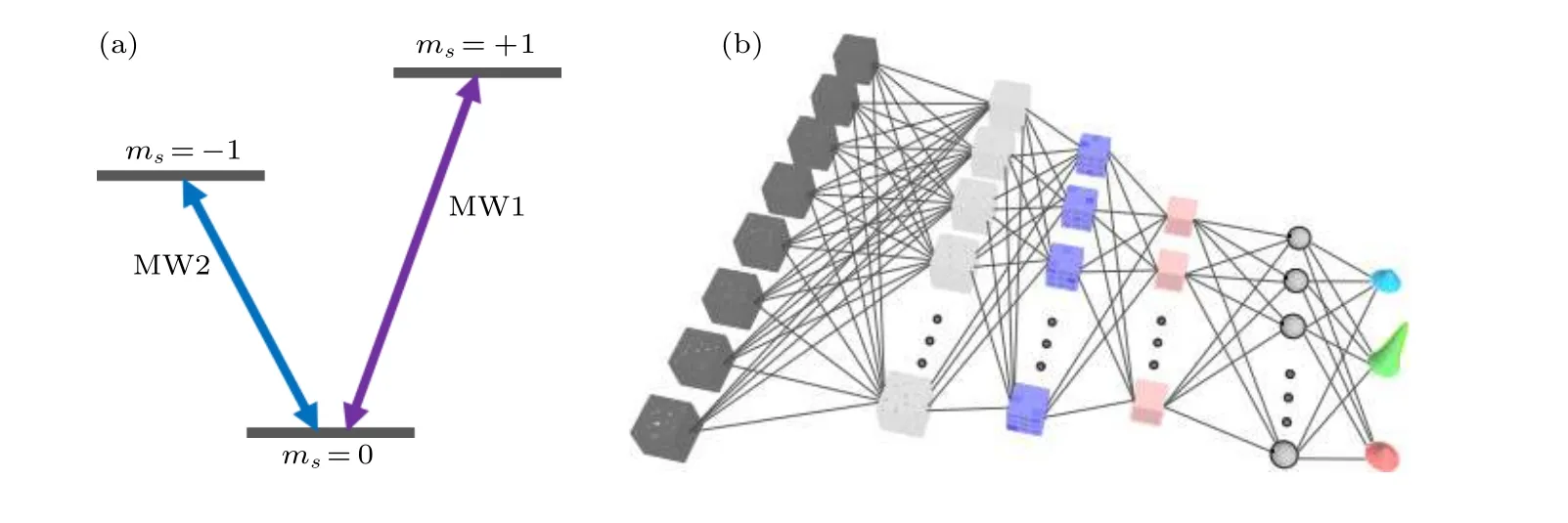
圖6 (a)利用共振微波操控NV色心基態能級; (b)可對拓撲相進行分類的3D卷積神經網絡的體系結構, 輸入是在10 × 10 × 10規則網格上的密度矩陣的實驗數據. 每個密度矩陣由八個實數表示. 輸出是每個可能相的分類概率[54]Fig. 6. (a) Using resonance microwave to control the ground state energy level of NV color center; (b) architecture of the 3D CNN to classify the topological phases. The input is experimental data of density matrices on a 10 × 10 × 10 regular grid. Each density matrix is represented by eight real numbers[54].
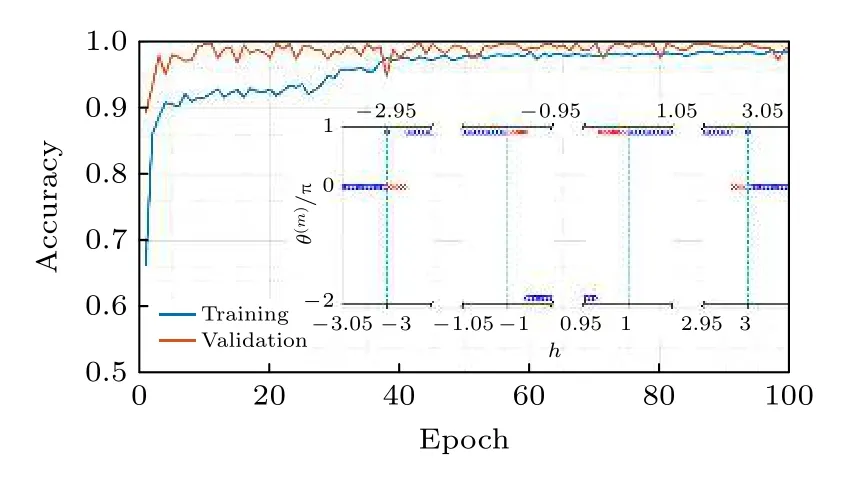
圖7 迭代次數增加時的訓練和驗證準確性. 訓練和驗證準確性在訓練過程開始時迅速增加, 然后達到了很高的飽和值(≈ 98%)[54]Fig. 7. The training and verification accuracy when the number of iterations increases. The training and validation accuracy increased rapidly at the beginning of the training process, and then reached a high saturation value (≈98%)[54].
訓練卷積神經網絡的方式將比傳統的方法更加有效. 首先, 對于未知序參量和拓撲不變量的拓撲相, 由于不需要知道各個拓撲不變量的精確解而只需要必要的訓練數據, 所以可以被更廣泛地應用在未知拓撲相之中. 再者, 沒有在常規網格上提供數據的情況下, 離散積分的常規方法無法使用.CNN在這方面具有更好的應用范圍. 因此在實驗中所需要的樣本也就更少. 并且, 機器學習是直接從混態之中提取數據, 而不需要依賴于純態定義的拓撲不變量. 這在量子實驗體系中是具有極大優勢的.
3.2 量子主成分分析
由于主成分分析(PCA)在對數據降維的同時能夠盡可能保留有效信息的特性, 其在機器學習領域有著十分廣泛的應用前景. 量子主成分分析(qPCA)由于量子算法的量子加速特性, 可以比經典算法更加高效地解決問題. 對未知的低秩密度矩陣的量子主成分分析以量子形式快速揭示了與大特征值相對應的特征值, 并為機器學習和數據分析提供了潛在的量子加速器. 對于qPCA, 如何萃取出其主成分一直是一個問題. 前文提到, qPCA算法解決了時間復雜度的問題, 但實驗上仍然需要大量的運算資源, 對量子比特數和操控的精確度都有著很高的要求, 所以完成實驗一直都是一件很困難的事情.
杜江峰課題組[57]基于金剛石NV色心體系利用量子機器學習完成了主成分分析算法(PCA),如圖8所示. 在實驗中使用了基于共振的量子主成分分析(RqPCA), 通過引入一個輔助比特, 實現了算法的量子指數加速.
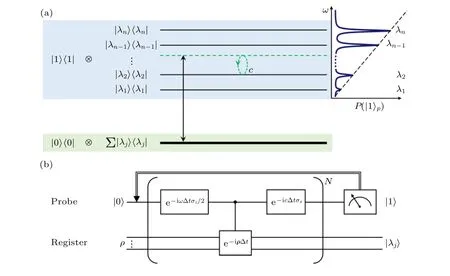
圖8 共振量子主成分分析算法原理圖 (a)探針-寄存器耦合系統的能級結構, | λi〉 是 ρ 的第 i 個本征態, 而 λ i∈[0,1] 是對應的本征值, 如果掃描頻率 ω ≈λi , 就會引起探針量子位的拉比振蕩; (b)使用Suzuki-Trotter分解的RqPCA的量子電路, 對探針量子位進行投影測量得到 | 1〉 表明該算法成功[57]Fig. 8. Algorithm schematic of RqPCA: (a) The energy structure of the coupled probe-register system. | λi〉 is the i-th eigenstate of ρ and λ i∈[0,1] is the corresponding eigenvalue. Once the scanning frequency ω ≈λi , the Rabi oscillations of the probe qubit is induced; (b) the quantum circuit of RqPCA. The projective measurement of the probe qubit in the state | 1〉 indicates success of the algorithm, with principal component being distilled in the register[57].
實驗體系的哈密頓量為H=|1〉〈1|?ρ+其中第一項為輔助比特與量子寄存器的耦合項, 第二項為所添加的可調能量偏執.In為與ρ維度相同的單位陣. 當施加一個以強度c驅動輔助比特的外場, 若ω≈λi, 則會發生從|0〉|λi〉 到|1〉|λi〉 的躍遷. 當初態制備到ρini=|0〉〈0|?ρ時,系統將在下面的哈密頓量下演化:
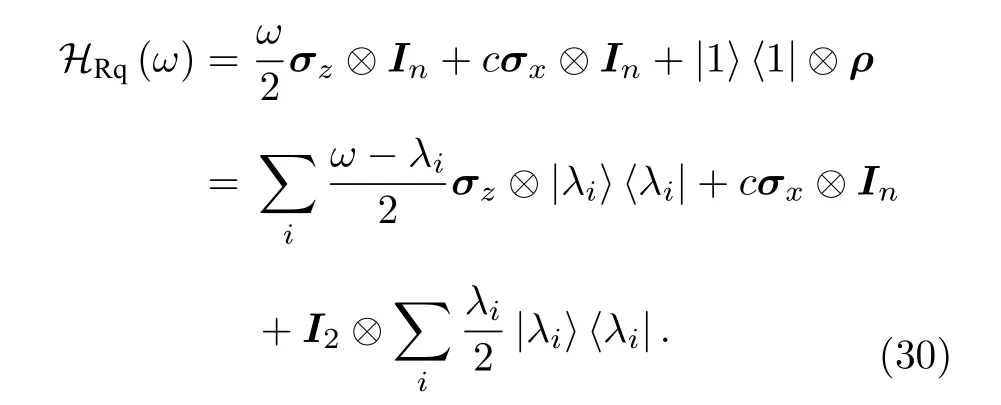
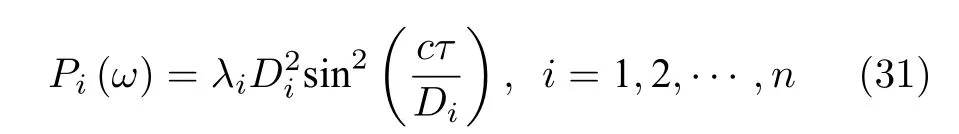
通過對ω進行掃頻, 當滿足某個特定λi, 探測比特會以的概率躍遷, 其中在實驗中, 通過測量探測比特在|1〉 上的布居度, 可以得到相應的譜線, 而每一個峰就對應一個相應的特征值. 對一個4 × 4的矩陣進行主成分分析, 其效率可達86%, 保真度可達0.90.
3.3 量子自編碼器
自動編碼器的想法在神經網絡領域已經流行了數十年, 通常是為了降低數據的維度. 它以一種無監督的方式學習有效的數據編碼, 包括一個編碼器, 用于學習一組數據的表示形式; 以及一個解碼器, 用于從簡化的編碼中生成盡可能接近其原始輸入的表示形式. 自編碼器通過簡單地學習將輸入復制到輸出來工作. 這一任務(就是輸入訓練數據,再輸出訓練數據的任務)聽起來似乎微不足道, 然而這過程有一個很大的難點, 那就是總要根據自己的需求去找到合適的方式來約束訓練的過程. 我們最常用的降維其實就是一個很好的例子, 限制數據的維度并不是一個簡單的過程. 我們所加的這些限制條件, 一方面要能夠滿足我們的要求(比如對噪聲的處理或者還原), 另一方面還需要能夠有效地防止程序機械的將數據復制輸出, 使其具有高效表達的能力.
受到經典自編碼器的啟發, 其在量子領域也可以用來解決一些傳統方法難以輕松解決的問題. 接下來我們介紹其中一種很有效的應用. 文獻[58]基于NV體系構建了量子自編碼器, 如圖9所示,并通過提高量子糾纏的壽命進行了驗證. 量子糾纏作為極為重要的量子資源, 卻又非常脆弱, 容易受到環境的干擾而發生退相干, 因此保護糾纏, 抑制退相干是量子領域里的核心話題. 有一種方法是將糾纏的有效信息通過機器學習的方式編碼到相干時間長的子空間, 而在需要取出信息時再進行反向解碼操作, 還原為原有信息, 這樣就變相的提高了量子糾纏的壽命.
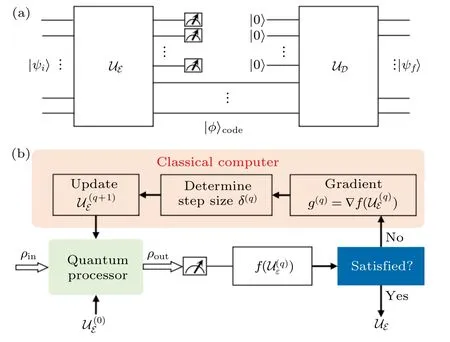
圖9 (a)量子自編碼器線路圖, 通過編碼操作 U E 將|Ψi〉中的信息壓縮到 | φ〉code 中, 在需要時通過解碼操作 U D 將|φ〉code 還原為 (b)優化編碼器的基于梯度算法的HQCA的 訓練過 程, ρ in 是編碼器的輸入狀態, ρ out 是輔助量子位的輸出狀態, 是成本函數, q是迭代次數[58]Fig. 9. (a) Quantum autoencoder circuit. The target information of | Ψi〉 can be encoded to the code state | φ〉code via the encoder U E. | φ〉code can be reconstructed to when needed by the decoder U D. (b) Training process of the gradient-based HQCA to optimize encoder. Here, ρ in is the input state of the encoder, and ρ out is the output state on the ancilla qubits. is the cost function, where q is the current iterative number[58].
文中基于參數化量子線路的思想構建編碼器,編碼器設定為共包含四個參數的操控算符, 四個參數分別對應兩束選擇性微波脈沖MW1和MW2的振幅和相位. 之后采用混合量子經典方法(HQCA)進行訓練, 由量子系統和經典系統共同組成訓練體系, 基于梯度算法對參數進行迭代, 成本函數和梯度的計算在量子系統中執行, 其余部分則由經典系統完成. 每次迭代都根據由量子系統測量得到的成本函數的值以及設定的步長來進行梯度運算, 以合適的學習率對參數進行調整更新, 直至其滿足實驗需求而完成迭代. 這種方式能夠緩解量子資源不足的問題, 同時經過機器學習過程也能抑制量子系統本身造成的實驗誤差. 本文基于金剛石NV色心體系對這種方法進行了驗證, 把電子自旋和核自旋的貝爾態中的糾纏信息編碼到相干時間較長的核自旋上進行保護, 使得糾纏的壽命由2 μs提升到3 ms, 提升超過了1000倍.
4 展 望
值得注意的是, 本文主要介紹了量子機器學習基于NMR和NV色心這兩種自旋量子體系在近年來的實驗進展, 并不是關于量子機器學習的全面綜述, 只介紹了這兩種實驗體系涉及到的部分量子機器學習算法. 除了這兩種體系, 量子機器學習在諸如超導[32,59]、光學[30,60]等體系中都有著良好的發展.
量子機器學習是近幾年新興的交叉研究領域,有著巨大的發展潛力. 雖然已經取得了一定的成果, 但是在未來的發展中依然存在著很多問題[14].首先, 在解決實際問題時, 需要將經典的信息導入到量子體系當中, 這個經典到量子的信息轉換過程本身就很復雜, 會耗費大量的資源, 目前仍沒有行之有效的方法. 其次, 常見的各類量子體系還都不夠成熟, 量子機器學習的發展在今后相當長的一段時期內仍將受限于量子比特的數目、相干性、可糾錯性等問題, 構建通用量子計算機或專用量子處理器仍十分困難. 最后, 對于已有的量子算法, 難以斷言其處理問題的過程中, 是否存在著超越經典算法的優勢, 同時也缺少評估量子算法有效性的系統性方法.
雖然還存在種種問題, 現階段量子機器學習在解決各學科領域的問題已經顯示出巨大優勢潛力,尤其是為一些常見的量子物理問題的分析和處理提供了一種有效的手段, 例如量子拓撲相的鑒定等[54,61-66], 未來必將能夠繼續助力各領域的突破和發展.

