量子生成模型*

孫太平 吳玉椿2)? 郭國平2)3)

1) (中國科學技術大學, 中國科學院量子信息重點實驗室, 合肥 230026)

2) (合肥綜合性國家科學中心人工智能研究院, 合肥 230088)

3) (合肥本源量子計算科技有限責任公司, 合肥 230026)

近年來, 很多基于生成模型的機器學習算法, 如生成對抗網絡、玻爾茲曼機、自編碼器等, 在數據生成、概率模擬等方面有廣泛的應用. 另一方面, 融合量子計算和經典機器學習的量子機器學習算法也不斷被提出.特別地, 量子生成模型作為量子機器學習的分支, 目前已有很多進展. 量子生成算法是一類量子-經典混合算法, 算法中引入參數量子線路, 通過執行參數線路得到損失函數及其梯度, 然后通過經典的優化算法來優化求解, 從而完成對應的生成任務. 與經典生成模型相比, 量子生成模型通過參數線路將數據流映射到高維希爾伯特空間, 在高維空間中學習數據的特征, 從而在一些特定問題上超越經典生成模型. 在中等規模含噪聲的量子體系下, 量子生成模型是一類有潛力實現量子優勢的量子機器學習算法.

1 引 言

在經典計算領域, 生成模型被廣泛應用于各個領域, 如圖像生成[1]、語音合成[2]、藥物設計[3]、圖像轉換[4]等. 近來已有對經典生成模型的量子版本的研究, 如量子生成對抗網絡[5,6]、量子玻恩機[7,8]、量子玻爾茲曼機[9-12]、量子自編碼器[13-15]以及量子貝葉斯網絡[16]等.

量子生成模型是受經典機器學習模型啟發, 使用量子計算機來改進經典模型中的生成步驟, 以完成數據生成、概率模擬任務的一類算法.

這類算法的主要步驟是, 通過量子線路生成量子態, 用量子態觀測結果構建損失函數, 再通過經典的優化算法進行迭代優化, 從而得到最優的參數變量集合以完成相應的生成任務. 因此, 這些算法被統稱為量子-經典混合算法. 這種量子-經典混合的閉環優化思想始于變分量子算法[17], 即通過量子計算機和參數化量子門操作集合獲得分子的量子態表示, 測量分子模型對應的哈密頓量的期望值, 以此作為目標函數進行變分優化.

量子相位估計[18]在大數分解[18]、HHL[19]等被證明有量子優勢的算法上具有廣泛的應用, 但基于以下原因相位估計算法無法在當前的計算體系下有效實現: 1) 當前硬件體系多集中于單量子門和兩比特糾纏門的實現, 相位估計用到的受控幺正門(c-Uj)必須分解為基本門的組合, 此過程會顯著降低受控幺正門的保真度; 2) 相位估計用到的量子傅里葉逆變換需要O(n2) (n為量子比特個數)數量級的量子門, 使得深層量子線路的態保真度無法達到量子計算要求. 量子計算體系的噪聲不可避免, 當前只有中等規模的量子比特、無法實現有效的量子糾錯[20]技術, 這使量子-經典混合算法受到廣泛關注.

盡管已有多種量子生成任務在真實量子芯片上完成, 如利用量子生成對抗網絡進行圖像生成與識別[21], 但對于參數量子線路(Parameterized Quantum Circuit, PQC, 見附錄)的表示能力與經典網絡相比是否具有優勢還缺少理論的結果.Du等[22]嘗試從內在的線路結構出發證明其結論,而經典深度學習神經網絡和量子線路的比較還沒有結論. 同樣的, 量子生成網絡作為量子機器學習的一部分, 如何將經典數據轉化為量子態、如何從測量結果獲取經典信息仍需要更直觀更普適的方法.

本文主要分析一些常見量子生成模型的優勢和劣勢, 并對其擴展性展開討論. 量子生成模型的分類與經典生成模型類似, 是以任務為導向的. 量子生成模型基本沿襲與之對應的經典生成模型的命名, 如量子生成對抗網絡是使用量子線路來完成經典生成對抗任務的一種量子生成模型. 對于利用量子體系特有的性質以完成生成任務的, 如量子玻恩機, 則是用量子專有的玻恩測量命名. 還有一些模型保留了原作者的命名方式, 歸并在“其他生成模型”這一節進行介紹. 一些量子生成模型如量子生成對抗網絡、量子玻恩機、量子自編碼器等用到的參數量子線路, 在附錄里會有詳細的介紹. 通過對這些模型的比較, 可以從不同角度理解量子生成模型的構建思路, 以此為不同的計算任務構建與之適應的計算模型提供啟發.

2 量子生成模型

2.1 量子生成對抗網絡

經典的生成對抗網絡[23](generative adversarial Network, GAN)被視為深度學習中的前沿進展. GAN在生成圖像[1]、語音[2]、文本[24]等方面具有非常廣泛的應用. 經典生成對抗網絡是一類有兩個玩家的博弈游戲, 一個是生成器(generator), 記為G, 另一個為鑒別器(discriminator), 記為D. 對于已存在的源數據→x～pdata, 生成器G生成新的數據以逼近真實的源數據分布, 使D無法區分數據的來源; 而鑒別器D對每個輸入數據給出真或假的決策概率, 以最大程度地區分這兩類數據.

如果G產生的數據足夠逼近目標數據, D無論對于何種輸入數據, 都有50%的幾率誤判, 這時生成對抗網絡就達到了Nash平衡點. 設真實的源數據標簽為1, 由G產生的數據標簽為0, D輸出(0,1)間的概率值, 那么生成對抗網絡的損失函數可以被定義為:

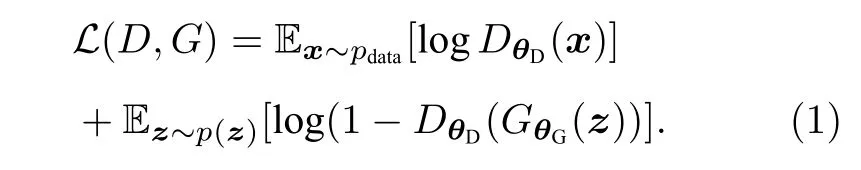
生成對抗網絡的訓練策略是, 更新其中一方的參數時, 另一方的參數保持不變. 對于上述的損失函數模型, 優化任務為 m inθGmaxθDL(D,G). 采用經典神經網絡構建的GAN模型, 可以用反向傳播算法來實現梯度計算.

量子的生成對抗網絡[5,21,25,26](quantum GAN,QGAN)基本保留了經典生成對抗模型的特征, 不同之處在于量子生成對抗網絡用到的數據集既可以是量子的也可以是經典的, 而且可選擇地, 生成器與鑒別器也可以為經典神經網絡或參數量子線路.

對于數據是量子的, 生成器與鑒別器也都是量子的情況, Dallaire-Demers等[5]提出了這樣的QGAN模型: 源數據的概率分布模型為pR(x) , 由某個未知(有可能很復雜)的過程R生成. 由參數θG確定的生成器G生成新的數據樣本, 由參數θD確定的鑒別器D識別這兩類數據. 用標簽λ指定源數據中的類別,, 考慮噪聲|z〉 , 可以按照(1)式定義與參數有關的損失函數L(θD,θG) , 這里D的輸入是R(|λ〉) 或G(θG,|λ,z〉)) :

其中含φ的項是調整源數據和生成部分占整體的比例. 一般取Dallaire-Demers等構建的量子生成對抗網絡線路圖如圖1所示.

圖1 量子生成對抗網絡結構[5]Fig. 1. The general structure of QGAN[5].

量子生成對抗網絡的任務就是通過參數優化來實現 m inθGmaxθDL(θD,θG) , 從而得到最接近于源數據概率分布的分布模型與鑒別模型. 量子線路的梯度可以用數值差分[27]、參數位移法則[27]、以及Hadamard test線路[5]來求. Dallaire-Demers在數值模擬上實現了源數據為|0〉,|1〉 兩個量子態的生成對抗任務.

Lloyd等[6]討論了當數據是量子的, 鑒別器是量子或經典的, 生成器是經典的量子生成對抗模型. Lloyd所述的量子數據是通過對一個量子體系進行固定的測量得到的數據分布. 根據量子優越性[19]的表述, 經典的生成器不能有效地匹配量子數據分布, 或者更準確地, 除非有指數的資源可用,經典的生成器無法模擬量子數據的分布pR(x). 對于數據是經典的, 生成器和鑒別器都是量子的情況, Lloyd通過對比得出, 經典的生成器和鑒別器在計算梯度時需要O(N2) 個比特和O(N2) 步時間(N是經典數據的維度), 而量子的生成器和鑒別器在計算協方差矩陣時, 如果矩陣是低秩和稀疏的,需要O(logN) 個量子比特和O(poly(logN)) 個邏輯門操作.

Zeng等[26]結合量子玻恩機構建了經典數據-量子生成器-經典鑒別器的量子生成對抗模型, 實現條帶圖(bars and stripes, BAS)[8,16,26,28]的概率生成與識別(見第2節). 類似的, Situ等[29]將BAS圖的每個點都編碼至量子比特上, 通過參數量子線路構建的生成器生成量子態, 測量結果輸入至經典神經網絡構建的鑒別器, 也實現了BAS圖的生成.Zouful等[25]通過測量量子態在計算基上的投影,將其轉化為數據對應的概率, 以此為基礎構建生成對抗網絡, 實現了對數正態分布、雙峰高斯分布等概率分布的學習和生成. 值得注意的是, 連續數據被截斷并舍入到臨近整數值, 所以該模型仍是離散數據的概率學習模型.

隨著量子硬件操控水平的提高, 在量子芯片上實現量子生成對抗網絡已經有相關的工作. Hu[30]等利用超導量子體系首次實現了具有量子數據、量子生成器、量子鑒別器的量子生成對抗網絡的實驗驗證, 生成保真度高達98.8%. 在Hu的實驗中, 量子數據為單比特量子態, 生成器參數為量子門旋轉角度. 在優化D或G時采用梯度下降算法, 量子系統的操控和測量通過FPGA(field programmable gate arrays)實現, 線路梯度通過經典計算機估算得到. 該實驗對于NISQ體系下的量子機器學習優勢的探索具有重要意義. 此外, Huang等[21]通過將測量量子生成器得到的數據作為經典圖像灰度值, 完成了手寫數字集0和1的生成對抗任務, 為量子比特資源受限條件下經典數據的生成提供了一個思路.

2.2 量子玻恩機

量子玻恩機[7,8](quantum circuit Born machine,QCBM)是基于波函數的概率解釋的一種模型. 量子玻恩機將概率分布編碼至初態上, 把量子態在計算基上的投影作為數據的概率. 量子玻恩機是一種隱式的生成模型, 因為我們實際上并不需要知道這個純態的密度矩陣, 而只需要知道疊加態振幅的模值. 這樣的設定對量子線路的結構限制也更少, 所以一般被認為具有更強的表示能力.

對目標概率分布 π (x) 進行采樣得到數據集D={x}, QCBM通過參數量子線路把初態|0〉 演化為|ψθ〉 , 并在計算基上的測量得到生成數據x～pθ(x)=|〈x|ψθ〉|2的概率分布. 訓練目標是讓模型的概率分布pθ接近真實數據分布 π (x). QCBM采用所謂的MMD(Maximum Mean Discrepancy)損失函數:

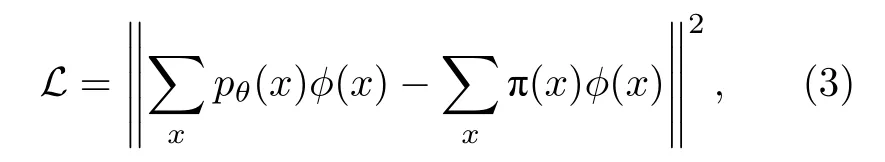
其中φ將x映射到高維Hilbert空間. 進一步地,定義核函數K(x,y)=φ(x)Tφ(y) , (3)式即可避免在高維空間中進行運算, 等價于

核函數可以取為高斯形式:K(x,y)=直接計算上述損失函數的梯度比較困難, 但可以證明, 下式無偏地等價于梯度:

其中pθ+(x) 和pθ-(x) 是在參數下 的模型輸出概率,是參數空間的第 (l,α) 個單位矢量(α和l分別表示迭代的步數與當前迭代的第l個參數的下標).

對所有量子比特進行測量, 會得到計算基上的概率分布. 源數據被映射為經典的比特流數據, 與量子態的計算基一一對應. 這種映射是一種同構,源數據空間和映射空間一樣大, 因此數據集的數據必須是有限的. 對于N個數據的集合, 需要n～O(log(N))個量子比特. 而生成線路中所用的量子門個數一般為O(poly(n)).

量子玻恩機是一種隱式生成模型, 模型本身并不涉及經典數據的特征維度, 甚至不涉及數據本身的形態. 在量子體系中不需要考慮數據的原本面貌是什么. 無論是圖片、數字還是文字, 都會被編碼為經典比特流數據. 一旦數據同構的方式確定了,基于量子線路的優化體系就與原本的數據形態無關了.

利用量子玻恩機進行概率分布的學習和生成在條帶圖(bars and stripes, BAS)[8,16,26,28]任務中取得很好的結果, 對于理想的無誤差測量, 量子玻恩機生成真實數據分布的比率為95.7%[8]. 此外通過對量子玻恩機的非計算基測量, 可以得到更多的信息, 這種方法可用來生成先驗概率分布, 如經典生成對抗網絡的先驗分布[31]. Cheng等[32]還從信息熵的角度比較了量子玻恩機與受限玻爾茲曼機[33,34], 為理解基于概率的生成模型和基于能量的生成模型提供了一個新的視角. Coyle等[35]提出一種量子玻恩機的子類—量子伊辛玻恩機—并引入量子核函數[36]來討論量子學習優勢.

2.3 量子玻爾茲曼機

與前述模型不同, 量子玻爾茲曼機[9-12](quantum Boltzmann machine, QBM)需要一種專用的量子計算機—量子退火機.

經典的玻爾茲曼機被廣泛用作機器學習的基礎工具, 例如深度信念網絡[37,38]和深度玻爾茲曼機[37,39]. 玻爾茲曼機是二進制數節點構成的概率生成網絡, 由可見節點和隱藏節點組成, 記為za,a=1,2,···,N, 其中N是總節點數. 這里為了和后面的量子生成模型保持一致, 取za∈{+1,-1}而不是za∈{+1,0}. 為區別可見節點和隱藏節點, 我們分別記為zν,zi. 同時用向量符號v,h,z=(v,h) 表示可見態、隱藏態和組合態. 在物理上其能量可以用伊辛模型表示:

其中ba,wab是在訓練的過程中進行需要優化的參數. 定義負對數相似度損失函數:

其中觀測到可見態h的概率為邊際分布Pv=那么玻爾茲曼機的任務就是優化哈密頓量的參量θ∈{ba,wab}, 使邊際分布盡可能接近真實的數據分布這樣就可以用梯度的方法來優化玻爾茲曼機:

其中 〈 ···〉 和 〈 ···〉v分別為對自由變量的玻爾茲曼均值以及對可見變量的玻爾茲曼均值.是雙重均值. 這樣我們就得到更新法則:

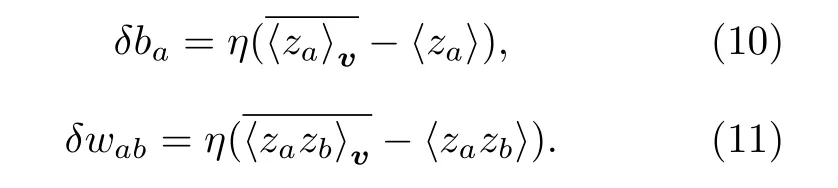
關于如何估算等式右邊的兩項均值, 在機器學習領域已經有較多的方案, 其中一個簡化的玻爾茲曼機模型—稱之為受限玻爾茲曼機(restricted Boltzmann machine, RBM)—已經成功的應用于實例[40].

量子玻爾茲曼機的出發點是使用作為物理實體的量子比特來替代經典的比特或節點. 然而不同的是, 量子力學體系的哈密頓量是 2N×2N維的矩陣. 而且量子力學算符大多是不對易的, 這對于求解梯度十分不便. 橫場伊辛模型的哈密頓量形式為:

其中I,σz,σx為泡利矩陣, 下標a表示作用于第a個量子比特. 與經典玻爾茲曼機類似, 定義配分函數和密度矩陣分別為:Z=Tr[e-H],ρ=Z-1e-H. 對于給定的可見態 |v〉 , 可定義邊際分布Pv=Tr[Λvρ],Λv=|v〉〈v|?Ih. 其 中Ih為 作 用在隱藏變量的單位陣.

那么類似地, 可以得到量子損失函數和對應梯度為:

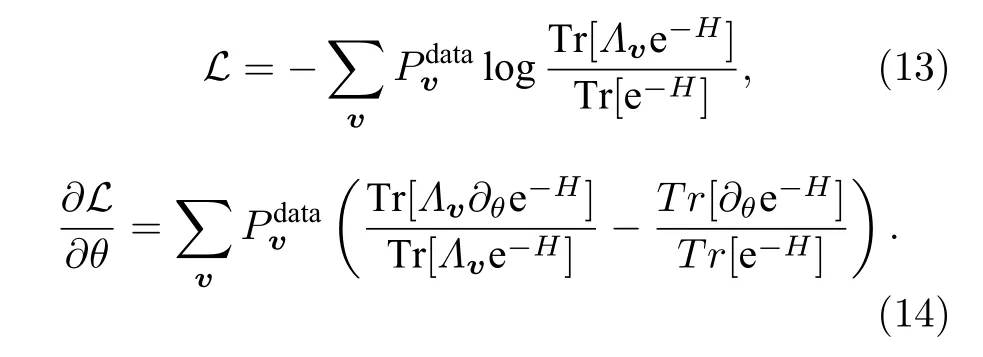
然而H和?θH并不對易, 也就是e-H?θH. 這樣在求解期望值的時候就會十分困難. 盡管Amin[9]通過分析的方法估算除了損失函數的界, 在一些特定的條件下可以估算損失函數的梯度, 但與前述量子生成模型相比, 參數更新的成本已然增加了.

盡管如此, 量子玻爾茲曼機仍然可以用來完成監督學習任務, 可以生成概率分布, 可以進行鑒別學習. Amin等[9]用量子玻爾茲曼機實現了伯努利分布的概率生成. Kieferová[12]用量子玻爾茲曼機設計了一種生成模型用以實現部分的量子態層析,并且除非BQP=BPP, 經典計算機無法有效地模擬其訓練過程. Dorband[41]在D-wave量子退火機上演示了量子玻爾茲曼機的構建過程. 但是, 相較于其他量子生成模型, 量子玻爾茲曼機帶來的近似誤差是難以避免的, 同時也難以說明相較于經典版本的優勢所在.

2.4 量子自編碼器

在經典的數據處理中, 通過機器學習中的自編碼器可以將數據從一個高維空間縮減到低維空間.經典的自編碼模型可以概括為: 通過參數化的神經網絡來訓練一個數據集, 其數據維度為 (n+k) , 得到擦除k個特征或維度的新數據, 如果這些數據可以通過解碼器(神經網絡)重新生成接近于原數據的一組新數據, 那么留下的n維數據被稱為壓縮數據. 這個過程被稱為數據壓縮. 數據壓縮對于處理稀疏特征數據集或高維數據集是十分直觀和有效的手段. 受此啟發, 量子自編碼器[13-15](quantum autoencoder)被設計為量子態壓縮的工具.

Romero等[13]提出的量子自編碼器與經典類似: 記{pi,|ψi〉AB}是 (n+k) 個量子比特上的純態集合, 子系統A和子系統B分別占有n和k個比特. 記Uθ為作用在 (n+k) 個比特上的幺正算符,其中θ={θ1,θ2,···}是參數集合, 以及|a〉B′為k比特寄存器的參考純態. 通過經典的優化方式, 我們希望平均保真度函數取得最大值:

其中ψiAB=|ψi〉〈ψi|AB, 以及aB′=|a〉〈a|B′.

量子自編碼器的核心在于, 如果想要有效地壓縮量子態, 必須保證態|ψi′〉=Uθ|ψi〉AB是A, B兩個子系統的直積態. 即當下式成立時, 才有C1=1 :

對輸出態進行量子態層析以確定其密度矩陣是非常困難的. 可以證明測量B和B'寄存器的態保真度等價于AB寄存器初態和末態的保真度(我們稱B寄存器輸出態為冗態). 這樣, 可以定義另一種平均保真度C2(θ) ,

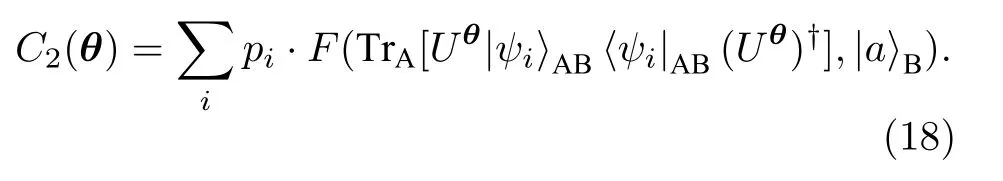
實際上求兩個態的保真度, 有一種SWAP測試線路可以完成[42].

通過參數量子線路來構建作用于AB系統的幺正變換, 并通過SWAP測試線路得到保真度信息. 取損失函數為L=-log(1-C2) , 采用經典方式進行優化, 可以得到保真度最高的參數線路, 這樣就實現了數據壓縮.

如圖2所示, 量子態壓縮模型可以由以下步驟來構建: 第一, 制備初態|ψi〉 和參考態 |a〉 , 并假設制備是有效的; 第二, 構建參數線路, 初態在幺正算符U下演化; 第三, 通過SWAP測試得到冗態和參考態之間的保真度.

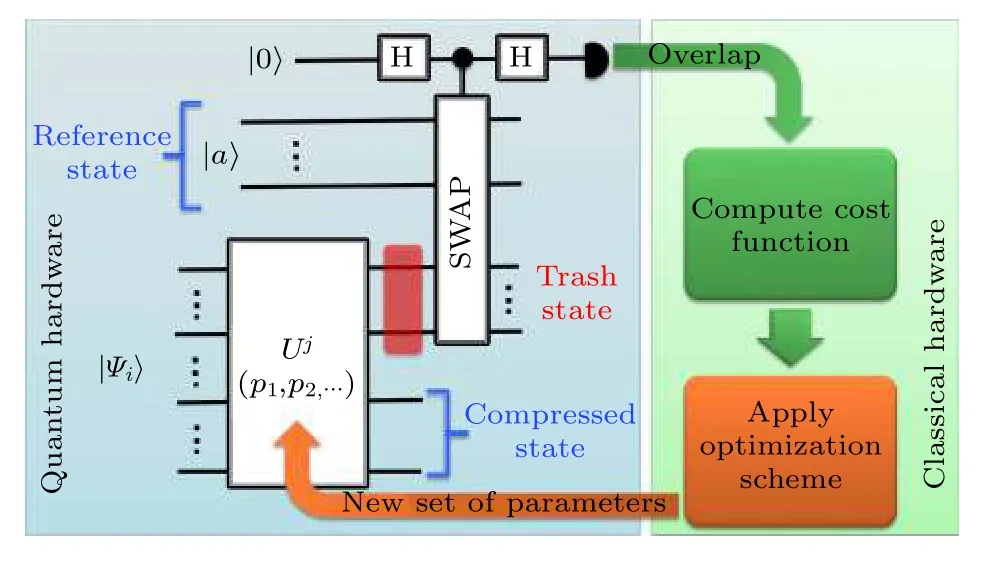
圖2 量子自編碼器的訓練示意圖, 其中 p 表示變量, 摘自[13]Fig. 2. Schematic representation of the hybrid scheme for training a quantum autoencoder where p represents variables, image from[13].

量子自編碼器在氫分子態的應用是一個成功的例證[13]. 其方法是用4 qubits來模擬氫分子, 通過變分量子求解器(VQE)求出對于固定原子間距的量子態, 以此作為量子自編碼器的輸入態. 氫分子的態并非占滿了4 bit的希爾伯特空間, 這就為量子態壓縮提供了可能. 直觀上看, 量子態壓縮的過程就像在整個希爾伯特空間中將若干子空間碎片像拼圖一樣拼接成緊密的空間. 量子自編碼器在量子加法器方面也有一定的應用[14], 這種加法器用以實現將兩個相同比特數的量子子系統編碼到一個新的子空間. Ding等[43]借助超導量子體系在實驗上驗證了量子加法器的可行性, 實驗保真度與理論值一致.

Pepper等[44]采用了Romero等[13]提出的量子自編碼器框架, 不同的是, 其數據壓縮任務是將多維量子比特(qutrit,|ψ〉=α|0〉+β|1〉+γ|2〉(已歸一化))壓縮為二維量子比特(qubit)態. 通過光量子實驗體系, Pepper等在實驗上實現了qutrits的壓縮, 并且證明了這樣的實驗優化系統對擾動是魯棒的. Bondarenko等[45]注意到經典數據通過經典自編碼器可以有效地去除噪聲, 因此量子自編碼器同樣有類似的作用. 通過構建以自旋翻轉噪聲和任意幺正門噪聲為主的GHZ含噪聲量子態, Bondarenko等驗證了量子自編碼器在量子數據去噪方面的作用.

如何判斷量子態能否通過量子自編碼器有效壓縮一直受到關注, Huang等[46]在理論上論證了實現有效量子自編碼態壓縮的條件, 并證明了若輸入數據的最大線性無關向量的個數不超過隱變量空間(壓縮后的低維空間)的維度, 那么量子自編碼器就可以無損地將高維數據壓縮至低維. Huang等利用量子光學體系在實驗上驗證了其理論的結果. 此外Cao等[47]提出可在量子退火機上運行、通過噪聲輔助的絕熱模型, 同樣可以完成量子自編碼任務. 同時, 對量子態壓縮的探索也使得量子梯度消失的現象—也即貧瘠高原的現象—得到進一步的研究[48].

2.5 其他生成模型

從前述量子生成模型可以看出, 經典機器學習給我們帶來了很多啟發. 類似地, 經典領域中因子圖(factor graph)可以作為概率生成模型, Gao等[49]提出了一種量子生成模型(quantum generative model, QGM), 并證明此模型可以高效地表示任意因子圖. 并且通過理論證明至少存在一些特定的概率分布, 可以被QGM有效表示, 但不能被任意具有多項式量級變量的因子圖有效表示. 如果多項式層次作為Pvs. NP問題的泛化是不塌縮的話,QGM相對于經典的因子圖具有指數優勢.

同時, 除了QGM的表示能力和泛化能力,Gao等[49]還提出了一種通用的量子學習算法, 該算法利用張量網絡、對多體糾纏量子態的父哈密頓量(parent Hamiltonian)構建、以及遞歸的量子相位估計進行學習. 顯然希望這種算法對任意問題都能在多項式時間內解決是不現實的, 但作者證明了至少存在一些問題, QGM相對于任意經典算法均有指數加速的效果, 前提是假設量子計算機不能被經典計算機有效地模擬.

直觀地理解QGM中的指數加速效果: 機器學習中的生成模型旨在通過尋找潛在的概率分布, 對自然界任意的數據生成過程進行建模. 由于自然界受量子力學定律支配, 用經典生成模型中的概率分布對真實世界中的數據進行建模具有很大的局限性. Gao等[49]提出的QGM模型, 用一個多體糾纏量子態的概率幅對數據的相關性進行參數化. 因為量子概率幅的相干性產生的現象比經典的復雜得多, QGM才有可能在特定情況下實現性能的顯著提升. QGM使用圖態|G〉 表示, 由m個量子比特與圖G構成. 如圖3所示.

圖3 經典和量子生成模型 (a) 因子圖表示; (b)張量網絡態表示; (c)量子生成模型定義[49]Fig. 3. Classical and quantum generative models: (a) Illustration of a factor graph; (b) illustration of a tensor network state;(c) QGM definition[49].

Gao[50]有另一篇工作同樣旨在發掘量子相關性在生成模型中的作用. 其中比較了經典貝葉斯網絡順序模型與對應的一維張量網絡, 展示了矩陣直積態(matrix product states, MPSs)比經典機器學習模型有更強的表示能力. 因為一維模型可以在經典計算機上被有效模擬, Gao等采用數值模擬的方式測試了真實數據集的生成, 發現MPS生成能力比經典模型有提升. 此結果為理解基于MPS的機器學習算法提供了新的視角, 因為有一類張量網絡子類不能有效地被經典計算機模擬, 但是可以在量子計算機上構建, 這就使得在機器學習中的生成模型框架下量子優勢是可能存在的.

除以上的量子生成模型外, 還有基于貝葉斯理論提出量子貝葉斯線路[16]. 這種量子線路引入輔助比特表示先驗概率分布, 通過受控操作傳遞給數據比特寄存器. 這樣可以極大地規避參數量子線路中出現的生成概率不均勻的問題.

3 量子生成模型展望

隨著量子計算機硬件的不斷發展, 量子生成模型也不只在量子虛擬機上得到實現, 基于真實量子芯片的生成模型受到了廣泛的關注, 但是量子生成模型存在的問題仍待解決.

首先, 量子生成模型是否可以生成任意概率分布的數據? 對于連續變量的數據, 量子生成模型還無法像經典神經網絡一樣有效地生成. 同時, 數據是量子還是經典的決定了生成模型的選取. 對于經典數據, 利用MPQCs或MPSs生成量子態, 對量子態的測量得到了量子信息的經典統計結果. 如何更有效地生成量子態以及如何從量子態讀取更多信息一直受到關注, 不同的量子生成模型給出了不同的策略, 然而對于任意連續變量數據的生成還需要進一步的探索.

其次, 量子生成模型作為量子機器學習的一部分, 如何體現量子計算的優勢, 仍然是一個開放性問題. 對量子線路的表示能力的研究為我們提供了一個思路, 但是對于不同的生成模型很難給出統一的表示能力定義. 而Gao等[49,50]從量子相關性出發, 直觀上將量子內在相關性的參數化來實現經典生成模型無法模擬的任務, 說明了量子優勢在機器學習領域中的存在性.

對于量子生成模型, 還需要進一步探索. 在量子領域, 量子生成模型提供了NISQ體系下可執行的算法, 在機器學習領域, 它引入了量子計算和量子信息的理念, 使機器學習算法突破經典計算的瓶頸成為可能.

感謝中國科學技術大學薛程博士和趙健博士的討論.

附錄A 參數量子線路

量子計算機遵循量子力學定律進行邏輯運算和信息存取. 而量子力學體系區別于經典體系之處在于, 由于疊加態和糾纏態的存在, 相同位數的量子數據比經典數據有著指數強的表示能力. 將量子信息轉化為經典信息需要對量子態進行測量.

量子計算的基本計算單位是量子比特(qubit), 單比特量子疊加態記為|ψ〉=α|0〉+β|1〉 (已歸一化). 根據玻恩的幾率解釋, 對單比特量子態進行測量, 得到0態的概率為|α|2, 得到1態的概率為|1〉. 對于多量子比特系統, 根據量子力學體系的完備性, 量子態可在計算基上展開, 由|Φ〉=測得任意態 |i〉 的概率為|ai|2. 對于泡利算符σi,i∈{0,x,y,z}, 其期望值可以通過算符的譜來計算, 即其中λj為本征值,|ψj〉為本征態. 對于一個更復雜的哈密頓量H, 我們總能將其分解為若干泡利算符的直積, 再分別求出各個部分的期望值,即m∈{0,x,y,z},αi,j,k...m為泡利基的實系數.

通過測量量子態在計算基上的投影或哈密頓量的期望值得到的經典數據, 其處理策略也根據量子生成模型的不同而有各式的差異. 如對于量子玻恩機, 量子測量得到的數據被映射為數據集的概率分布, 顯然這樣對于小型數據集或稀疏數據集有表示優勢. 而對于量子生成對抗網絡, 測量得到的數據可直接作為生成數據以混淆源數據.

量子生成模型的核心在于利用量子計算機生成量子態,對量子態進行測量得到經典的有效信息. 如何有效地生成量子態, 是我們面臨的首要問題. 參數量子線路(PQC)為這一問題提供了一個思路.

參數量子線路一般由若干單量子門和多量子糾纏門組合得到, 單量子門可以是任意單比特幺正門US(θ) , 常用的有泡利旋轉門多量子門一般采用UCZ=|0〉〈0|?I+|1〉〈1|?σz,UCNOT=|0〉〈0|?I+|1〉〈1|?σx等兩比特門. 單量子門和多量子門交替的結構極大地提高了態的糾纏能力, 擴展了態的表示空間.

記量子線路的參數為θ, 則參數量子線路可以用U(θ)表示. 若要保證參數量子線路是有效的, 其參數總量和線路深度都有相應的限制. 一般設定參數的總量是多項式級的,即n～O(poly(N)) , 其中n為參數個數,N為量子比特個數.同時線路的深度也設為多項式級的, 即L～O(poly(N)).

如何使參數量子線路有更強的表示能力一直受到關注.最直觀的方式是增加參數量子線路的深度, 構成MPQCs(multiple parameterized quantum circuits). 然而MPQCs的線路深度至多為多項式級的才能滿足有效性要求, 也即圖A1中的PQC模塊數是常數級的, 不隨量子比特數目增長. 而且由于量子噪聲的存在, 增加PQC的模塊數會極大地影響量子態的保真度, 所以在真實的任務中往往會限制PQC的模塊數. 除此之外還可以通過非計算基補充測量的方式, 來獲取更多的數據信息, 這種方法在QCAAN線路[31]中被提到.

圖 A1 參數量子線路示意圖Fig. A1. Illustration of MPQCs.

對經典神經網絡的表示能力的研究是一項非常重要的課題, 參數量子線路的表示能力直接關系到其能否體現量子優越性. Du等[22]證明了在多項式層次結構保持的前提下, 具有O(poly(N)) 個門的參數量子線路, 其表示能力比具有O(poly(N)) 個參數的經典玻爾茲曼機要強. 盡管如此, 參數量子線路和經典神經網絡的直接比較還有一些困難, 如何定義對量子和經典體系均適用的表示能力指標, 以及參數量子線路能否體現量子的優越性, 仍是開放性的問題.