基于蛛網結構的量子衛星廣域網構建策略及性能仿真*

聶敏 韓凱捷? 楊光2) 張美玲 孫愛晶 裴昌幸

1) (西安郵電大學通信與信息工程學院, 西安 710121)

2) (西北工業大學電子信息工程學院, 西安 710072)

3) (西安電子科技大學, 綜合業務網國家重點實驗室, 西安 710071)

量子衛星通信是通信領域的研究熱點和前沿, 具有理想的信息安全性和覆蓋面廣的優勢, 對于構建全球范圍的量子衛星廣域網具有重要意義, 而遠距離傳輸信息時網絡的可靠性、安全性和路由中繼等問題仍需改進. 為了構建性能良好的量子衛星廣域網, 本文提出利用蜘蛛網作為一種獨特的自然通信拓撲結構, 將自然界蛛網演進為人工蛛網拓撲, 量子信息的傳輸采用N階量子隱形傳態路由方案, 其傳輸時延基本不變, 在此基礎上構建蛛網網絡拓撲量子廣域網傳輸模型, 并對構建的網絡模型的誤碼率、吞吐率、安全密鑰生成率進行仿真分析. 用抗毀度作為衡量網絡拓撲結構可靠性的指標, 以9節點環型網和9節點蛛網為例進行定量和定性分析, 得出蛛網拓撲具有更高的可靠性. 當噪聲的平均功率譜密度給定且不存在中繼時, 量子態的傳輸距離越大誤碼率越大, 這時要考慮引入中繼; 當傳輸距離和噪聲功率譜密度一定的情況下, 誤碼率隨著中繼節點個數的增多而減小, 因此在蛛網拓撲下要選擇合適的路由過程. 隨著量子衛星分發糾纏光子對成功概率的增大, 吞吐率逐漸增加; 隨著網絡中傳輸時延的增大, 吞吐率逐漸減小, 但在該路由方案下傳輸時延基本不變, 且蛛網結構的傳輸時延很小, 因此本文中提出的基于N階量子隱形傳態的蛛網網絡拓撲量子廣域網的吞吐率不會有明顯的降低. 當量子信息的傳輸距離不斷增大時, 網絡密鑰生成率逐漸減小; 隨著網絡中繼節點個數的增多, 密鑰生成率逐漸增加. 由此可見, 利用蛛網拓撲以及N階量子隱形傳態路由方案構建量子衛星廣域網具有很好的優勢.

1 引 言

發展量子衛星通信是我國重點戰略發展計劃,其發展的最終目標是構建全球廣域量子通信網絡體系[1]. 量子密鑰分發(quantum key distribution,QKD)以其無條件安全性引起了學者的廣泛關注[2], 1984年Bennett和Brassard提出了第一個無條件安全傳輸的BB84協議, 1992年Bennett在此前研究的基礎上又提出了B92協議. 但在實際QKD實現過程中會存在很多安全漏洞, 2012年Lo等[3]首次提出測量設備無關量子密鑰分配(measurement-device-independent quantum key distribution, MDI-QKD)協議, MDI-QKD的提出不僅保證QKD協議理論上的安全性, 也消除了竊聽者的攻擊, 且使通信距離擴大. 隨著該協議理論基礎的不斷完善, 近幾年該領域的實驗得到了快速的發展, 2020年潘建偉等[4]提出了遠距離自由空間MDI-QKD方案, 實現了在19.2 km的城市大氣通道上的第一個自由空間MDI-QKD, 這項實驗標志著我國向著基于衛星的MDI-QKD邁出了第一步. 同年Yin等[5]實現了基于糾纏的無中繼千公里量子保密通信, 這些研究進一步表明通過量子衛星構建全球量子通信網絡的方案是可行的.

2016年8月, 我國成功發射了世界第一顆量子科學實驗衛星“墨子號”[6]; 2017年9月, 總長2000多公里的“京滬干線”量子保密通信網絡正式開通, 同時“京滬干線”與“墨子號”成功對接, 首次實現了洲際量子保密通信[7]; 2011年, 周小清等[8]研究了量子隱形傳態網絡的互聯與路由策略. 2012年, 連濤和聶敏[9]通過分析環境噪聲對量子信令遠距離傳輸的影響, 提出了基于糾纏交換的量子信令中繼策略. 2013年, 劉曉慧等[10]提出了傳輸時延小的多階量子隱形傳態量子路由方案, 并分析了其路由策略. 2021年聶敏等[11]根據球形蒲公英量子衛星網絡的結構特性, 提出了一種兩端糾纏交換的量子路由方案. 2021年1月陳宇翱等[12]提出了約4600 km的天地一體化量子通信網絡.

通信網絡的傳輸能力主要與網絡的拓撲結構和路由策略有關, 自然界中的蛛網結構相比于其他結構(樹型、星型、環型等)可靠性高、可擴展性好、傳輸時延小, 迄今為止國內外有關基于蛛網網絡拓撲的量子衛星廣域網構建策略研究尚未完全展開. 受自然界蛛網的啟發, 本文對其進行標準化處理, 在此基礎上分析蛛網結構和量子衛星通信網絡之間的相似性, 構建量子衛星廣域網, 進一步分析基于N階量子隱形傳態的量子衛星廣域網的誤碼率、吞吐率以及安全性問題, 通過仿真研究, 為構建性能良好的量子衛星廣域網奠定基礎.

2 蜘蛛網網絡拓撲

2.1 蛛網結構及其捕食策略

蛛網結構中圓網是最具代表性的, 且在圓網結構的基礎上可以繼續進化為別的類型的網[13]. 自然界中的圓形蜘蛛網如圖1所示, 結構圖如圖2,其呈現橢圓形并具有一定的對稱性, 由捕絲、拖絲、旋轉螺旋絲組成, 拖絲按功能又可以劃分為框架絲、錨定絲、徑向絲. 捕絲具有一定的黏性, 可將獵物粘住; 徑向絲支撐整個網結構的穩定[14], 且具有很強的延展性, 可以通過徑向絲的振動為蜘蛛提示獵物的位置.

圖1 自然界圓形蜘蛛網Fig. 1. Round spider web in nature.

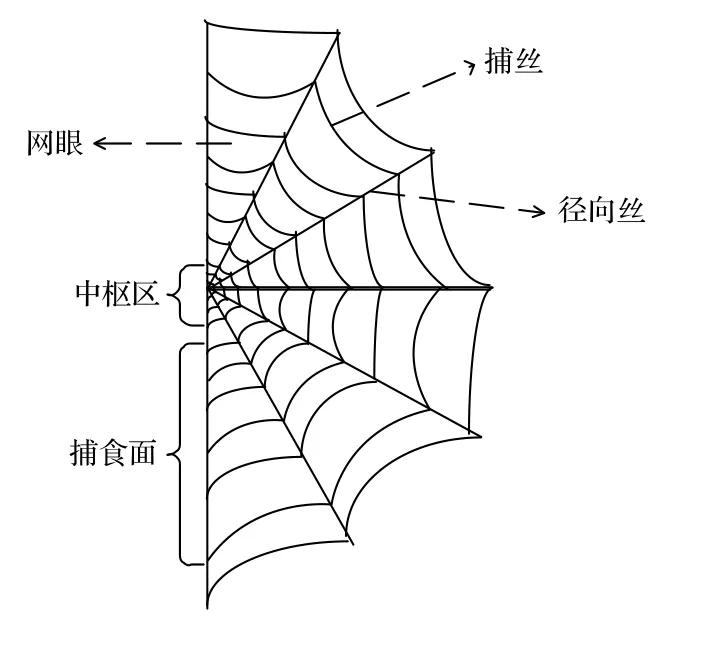
圖2 蛛網結構圖Fig. 2. Cobweb structure diagram.

蜘蛛一般停留在中心區域, 當獵物撞擊蛛網時黏性的捕絲會粘住獵物. 因蜘蛛的視覺能力很差,蜘蛛捕食主要依靠絲線的振動來判斷獵物的位置,振動信號沿徑向衰減率是沿周向衰減率的1/6[15],因此傳遞蛛網內的振動信息主要是沿著徑向絲快速傳遞到中心區域, 蜘蛛沿著徑向絲抵達獵物身邊.

2.2 人工蛛網演進過程

人工蛛網演進過程如圖3所示. 蛛網是由星型、環型拓撲演進而來, 其中星型結構簡單且容易管理; 環型拓撲的信息傳輸誤碼率很低, 但可靠性差. 蛛網網絡拓撲(spider network topology, SNT)除結合這兩種拓撲結構的優點之外, 還有很強的抗毀能力, 當通信鏈路發生故障斷開或者出現擁塞時, 由于網絡中任意一個節點到另外一個節點的路徑不止一條, 可以選擇其他路徑實現鏈路之間的連接, 使得信息有效傳輸.

圖3 人工蛛網演進過程 (a) 星型; (b) 環型; (c) 蛛網Fig. 3. Evolution of artificial cobweb: (a) Star; (b) ring;(c) spiderweb.

2.3 SNT與環型拓撲的性能分析

1)可靠性定量分析

網絡抗毀性考慮的是網絡拓撲在節點或邊失效后繼續維持功能的能力, 點(邊)連通度是最早被用來刻畫網絡抗毀性的測度指標. 因此本文網絡抗毀度從網絡拓撲結構的角度出發, 分析網絡發生故障前網絡保持連通的能力, 根據鏈路連通性分析網絡可靠性. 以9節點環型網絡和9節點SNT為例進行定量分析, 驗證蛛網結構的高可靠性. 抗毀度的計算過程如下, 首先計算完整的網絡拓撲的連通度, 然后算出每個節點的重要度, 刪除掉重要度最大的節點以及節點相連接的鏈路, 查看網絡中是否有節點連接, 重復上述過程直到網絡中沒有節點相連, 從而計算出網絡的抗毀度.

假設網絡拓撲H有g個節點, 刪除其中的c個節點后, 網絡拓撲可以表示為H(c) , 最終刪除m個節點可以使得網絡中的所有節點均為孤立節點, 根據參考文獻[16,17]可知, 網絡抗毀度定義為

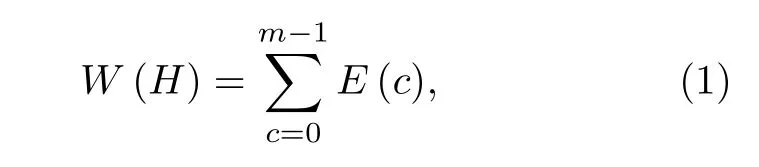
其中E(c) 表示刪掉c個節點之后網絡的連通度,表達式為:

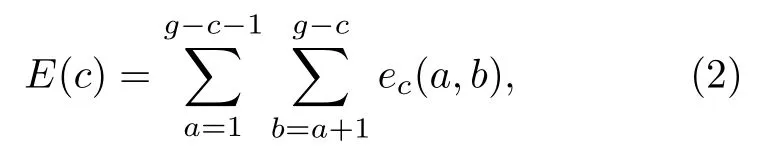
式中ec(a,b) 表示刪掉c個節點之后節點a和節點b之間的連通度, 可表示為:

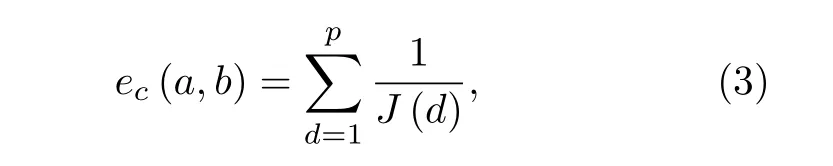
p為節點a到達節點b之間的路徑條數, 且均為互不相交的路徑;J(d) 為節點a到節點b之間的第d條路徑所需要經過的鏈路個數.

由上述的分析過程, 計算得到9節點環型網的抗毀度為

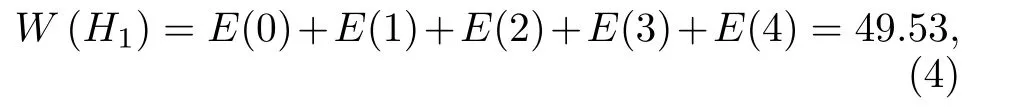
9節點SNT的抗毀度為

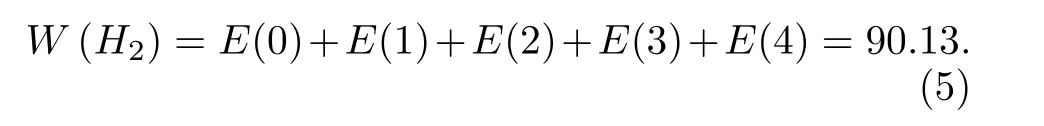
因此蜘蛛網絡拓撲結構相比環型網絡拓撲結構具有更高的可靠性.

2)可靠性定性分析

參考文獻[18], 假設鏈路失效的概率為r, 鏈路有效的概率為s, 網絡的全端可靠性為K(H,S) ,H代表網絡的拓撲結構,H-q是網絡H中除去q后獲得的網絡,H/q是網絡中將q所連接的兩個節點進行合并后得到的網絡. 只分析因鏈路失效而導致的不可靠性, 因子定理為

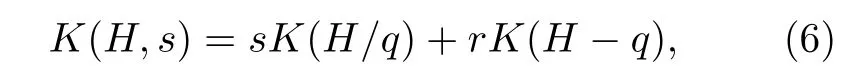
通過分解環型拓撲, 可以得到環型拓撲的可靠性為

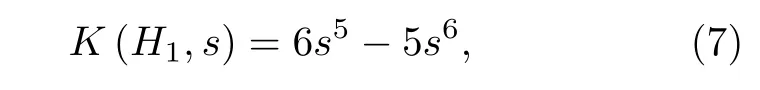
單層人工蛛網網絡拓撲結構經過分解, 最終可得到其可靠性為

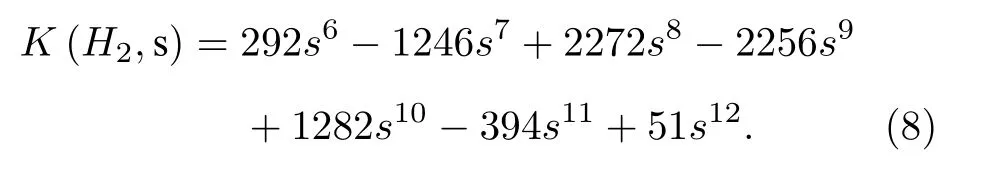
仿真實驗結果如圖4所示, 橫軸為鏈路有效率s, 縱軸為可靠性K. 當鏈路有效率為0.7時, 環型拓撲的可靠性為0.42, 蛛網拓撲的可靠性為0.81.因此蛛網結構在可靠性方面更具優勢, 隨著節點個數的增多, 網絡中任意兩個節點之間的通信路徑不止一條, 網絡全端可靠性增加.

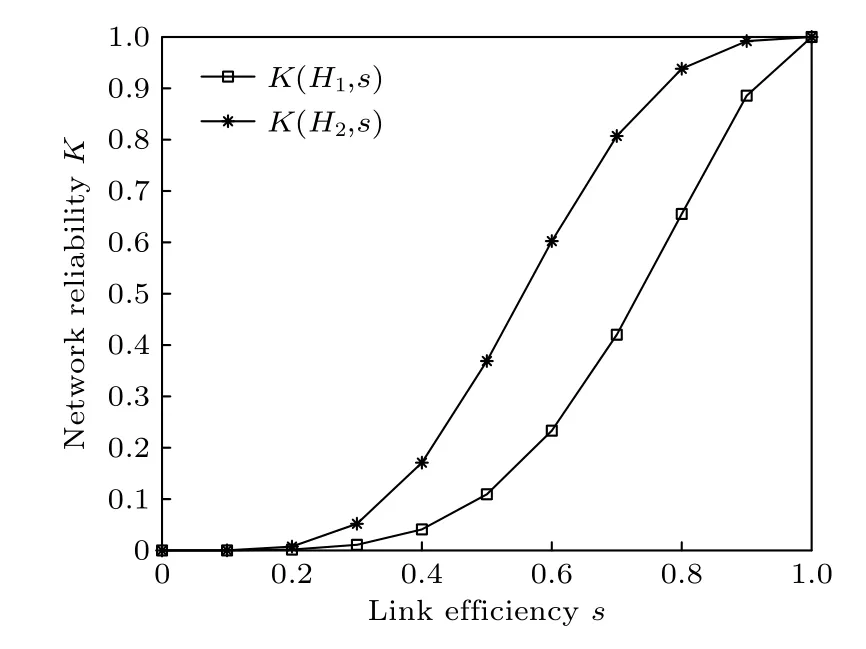
圖4 環型與蛛網拓撲的網絡可靠性分析Fig. 4. Network reliability analysis of ring and cobweb topologies.

3 基于N階量子隱形傳態路由方案

實現量子通信的關鍵是量子態遠程傳送和量子路由, 不同用戶之間需要共享量子糾纏[19,20]. 在進行遠距離節點的量子態傳輸時, 主要存在以下兩個問題: 一是量子終端的存儲容量有限, 當網絡中有很多中繼節點時, 其中一個量子設備不可能存儲所有可能與之通信的量子設備的糾纏光子對; 二是自由空間中充滿了各種環境噪聲, 進行遠距離的EPR光子對的分發是不可能的. 而N階量子隱形傳態路由方案是不受這兩個問題的限制, 可將量子信息從源節點Alice傳輸到另外一個遠距離且不與之共享EPR糾纏光子對的目的節點Bob處, 需在各個中間節點處進行量子測量和量子門操作, 通過中間節點完成量子態的傳輸[10]. 該路由方案原理如圖5所示

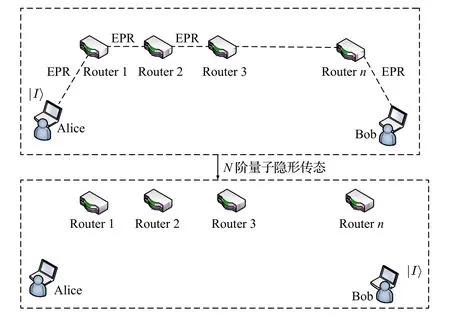
圖5 基于N階量子隱形傳態的量子路由方案Fig. 5. Quantum routing scheme based on N-order quantum teleportation.

3.1 二階量子隱形傳態

以二階量子隱形傳態過程為例進行分析, 假設Alice為源節點, Bob為目的節點, David為中間交換節點, 邏輯線路圖如圖6所示.

圖6 二階量子隱形傳態邏輯線路圖Fig. 6. Second-order quantum teleportation logic circuit diagram.

首先給Alice和David分發EPR糾纏光子對,給David和Bob分發EPR糾纏光子對, 糾纏態分別表示為

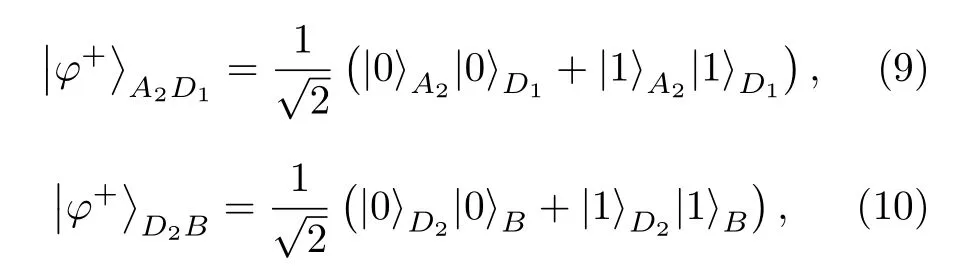
所以在開始進行信息傳輸時, 總的五量子比特系統可以表示為

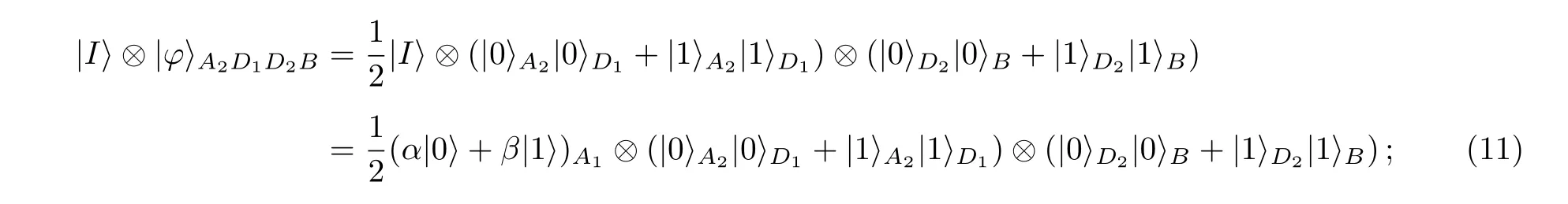
接著Alice和David對他們的兩個量子比特進行量子門CNOT操作, 得到如下結果:

然后Alice和David分別對他們的第一個量子比特進行哈德曼門操作, 得到如下結果:

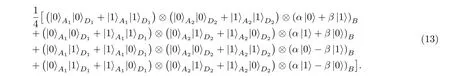
由上述計算結果可以看出, 只要Bob獲得了Alice和David的兩個量子比特的狀態信息, 就可以知道自己的狀態信息. 例如Bob已知Alice的兩個量子比特分別為|0〉A1|0〉A2, David的兩個量子比特分別為|0〉D1|1〉D2, 那么Bob的量子比特一定是α|1〉+β|0〉. Bob得知自己的狀態信息后, 就可以對其進行相應的量子門操作恢復出Alice傳輸給它的信息|I〉=α|0〉+β|1〉. Bob需要進行的量子門操作如表1所列.

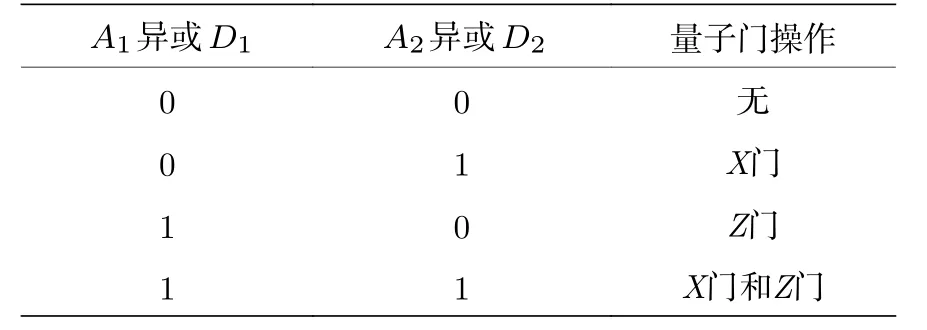
表1 已知測量結果后的量子門操作Table 1. Quantum gate operation after known measurement results.

3.2 三階量子隱形傳態

在分析二階量子隱形傳態的基礎上, 討論三階量子隱形傳態的具體過程, 其需要借助兩個中間節點完成量子態傳送. 源節點為Alice, 目的節點為Bob, 中間節點分別為David和Gina, 邏輯線路圖如圖7所示.

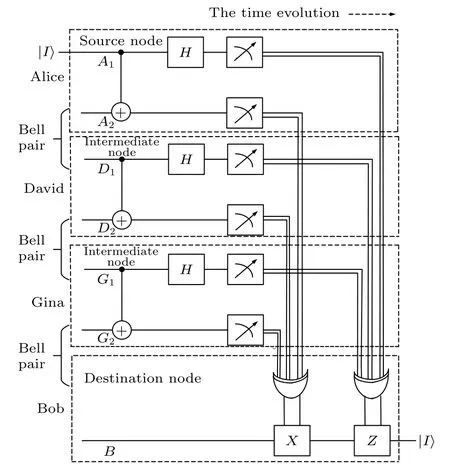
圖7 三階量子隱形傳態邏輯線路圖Fig. 7. Third-order quantum teleportation logic circuit diagram.

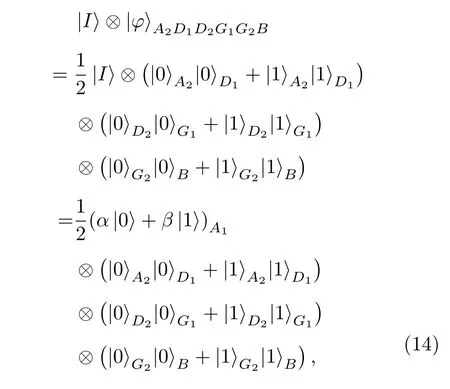
與二階量子隱形傳態過程類似, 在開始進行傳輸時總的七量子比特系統可以表示為接著采用與二階過程同樣的操作, Alice, David和Gina對他們的兩個量子比特進行量子門CNOT操作, 然后Alice, David和Gina分別對他們的第一個量子比特進行哈德曼門操作. Bob已知測量結果以后需要進行量子門操作, 如表2所列.

表2 已知測量結果后的量子門操作Table 2. Quantum gate operation after known measurement results.

綜上所述, 隨著網絡規模的不斷擴大, 就需要使用一個或者一個以上的中繼節點完成遠距離量子態傳送, 即N階量子隱形傳態過程. 由二階以及三階量子隱形傳態邏輯線路圖可知, 各個節點的量子門操作和量子測量是同步完成的, 完成多個節點路由時間與量子隱形傳態時間相同.

3.3 量子路由方案仿真分析

已有的路由方案很多, 常用的包括量子中繼路由方案、量子糾纏交換路由方案等. 參考文獻[10],設采用量子中繼路由方案時, 傳輸時間T為

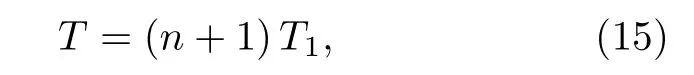
其中T1表示在量子信息的傳輸過程中完成量子隱形傳態的時間,n是路由過程使用的中繼節點數目.

采用量子糾纏交換路由方案時, 傳輸一個量子態所需要的時間T′為

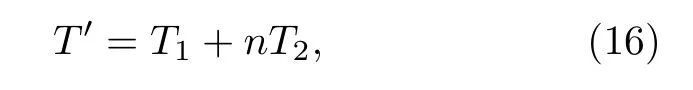
其中T2表示量子糾纏交換時間.

采用N階量子隱形傳態路由方案時, 傳輸一個量子態所需要的時間T′′為

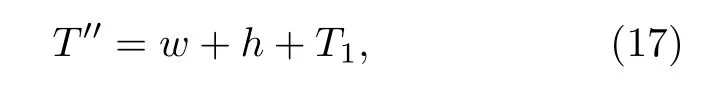
其中w為在廣域網的位置數據庫中查找用戶具體位置所需的時間,h為量子衛星分發糾纏光子對的時間. 假設T1= 0.8 μs,T2= 0.7 μs,w=0.01T1,h=0.01T1.

仿真結果如圖8所示, 當n=4 時,T= 4 μs,T'= 3.6 μs,T''= 0.82 μs; 當n=10 時,T= 8.8 μs,T'= 7.8 μs,T''= 0.82 μs. 由此可見, 隨著中繼節點個數的增多, 前兩種路由方案傳輸時延有明顯的增大, 而N階量子隱形傳態路由方案傳輸一個量子態的時間基本保持不變, 傳輸時延小.

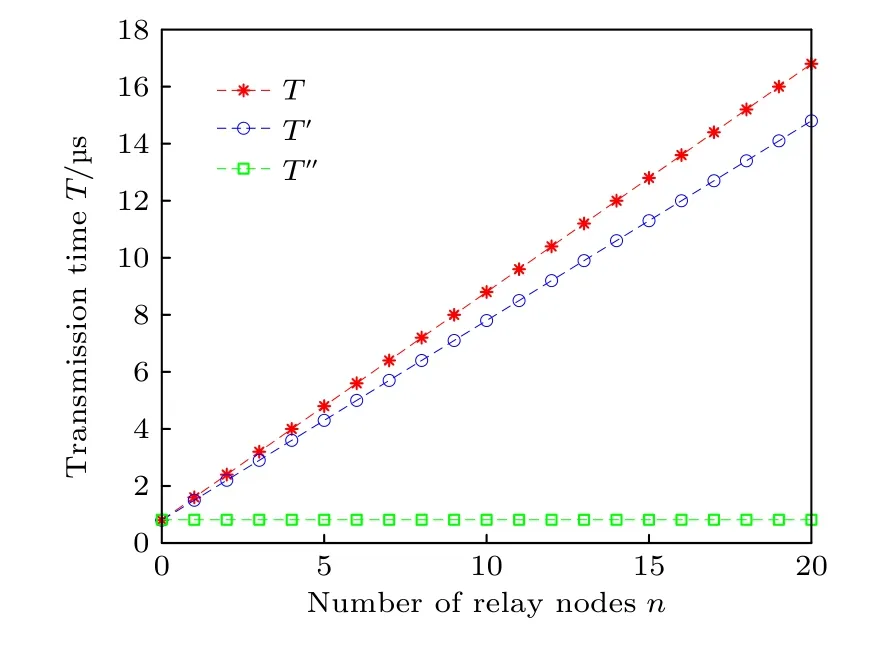
圖8 三種路由方案量子態傳輸時間與中繼節點個數的關系Fig. 8. Relationship between the quantum state transfer time and the number of relay nodes.

4 基于SNT的量子衛星廣域網網絡模型

自然界中的蛛網結構與量子衛星通信網絡有很多的相似性.

1)蜘蛛捕食獵物的大小決定所構建蛛網的大小, 說明蛛網具有很強的可擴展性, 因此要實現可靠性高的量子衛星廣域網, 就要采用蛛網網絡拓撲結構, 一個網絡的通信總需求決定了它的通信容量、大小和性能要求.

2)蛛網中的每個節點代表網絡中的一臺路由器, 量子信息通過路由器進行傳輸. 蛛絲的強度代表著通信網絡數據流的大小, 捕絲的延展性代表了它們適應通信流的能力.

3)在捕食過程中如果蛛網出現斷裂, 蜘蛛不會立即去修復破損的網, 而是利用其繼續捕食, 說明蛛網具有很強的抗毀性, 它將在夜晚根據環境變化以及捕食經驗構建新的網. 根據以上幾點的相似性, 以7節點SNT為例, 將其拉伸為立體結構來構建量子衛星廣域網, 其立體蛛網結構圖如圖9所示.

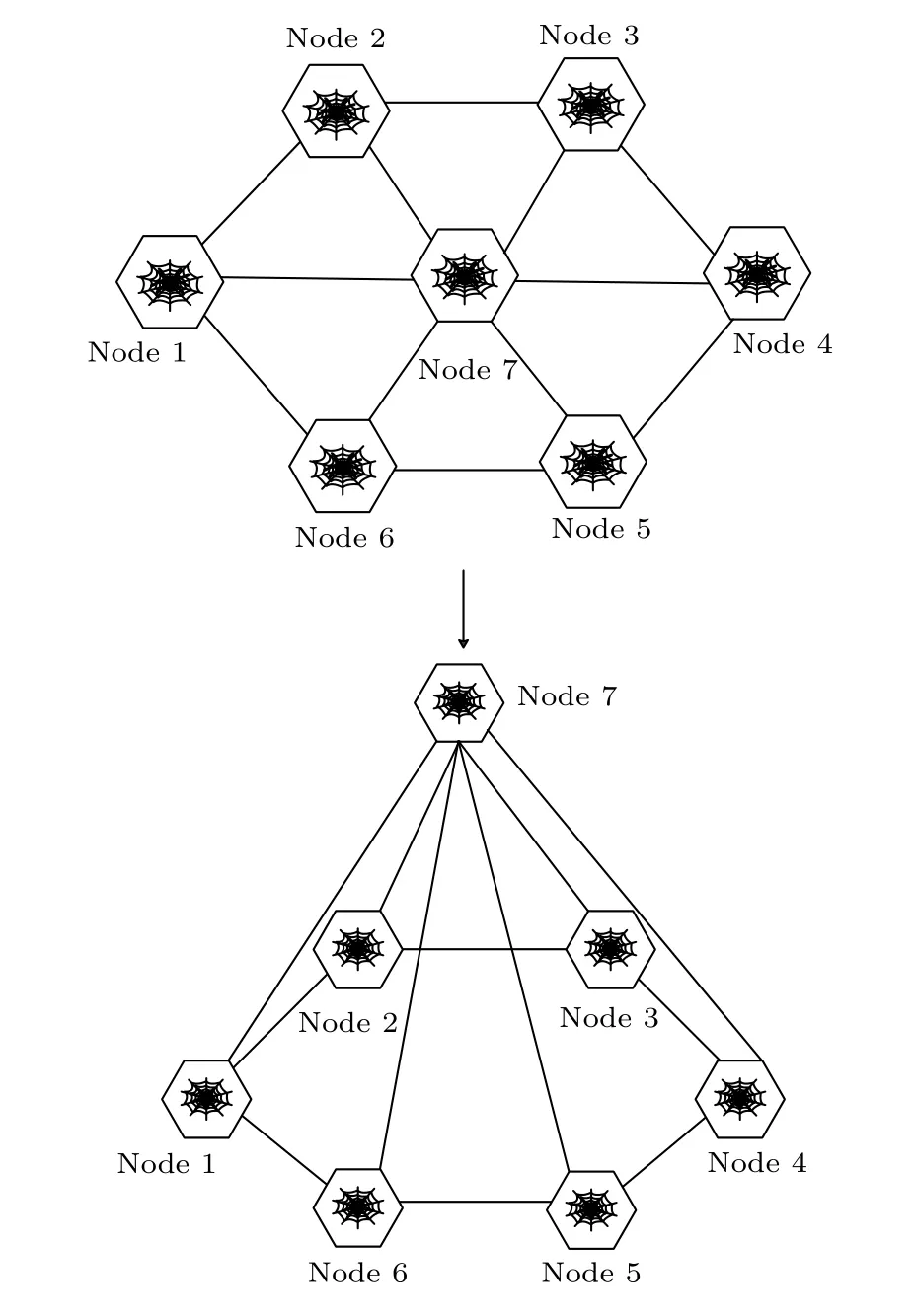
圖9 六邊形邏輯蛛網拓撲模型Fig. 9. Hexagonal logic spider web topology model.

圖10 是SNT量子衛星廣域網模型, 量子衛星廣域網由量子衛星(quantum satellite)、量子無線基站(router)、量子全局位置數據庫(QGPW)、量子局部位置數據庫(QLPW)以及地面通信用戶組成. 蛛網的中間節點作為quantum satellite, 其余蛛網節點為各個不同的基站, 作為中繼轉發, 每個基站都配有一個QLPW, 用來查找各個用戶的具體位置. 量子衛星的主要任務是生成糾纏光子對,并將其發送給各個基站, 建立衛星與各個基站之間的量子信道, 實現量子信息的傳輸.

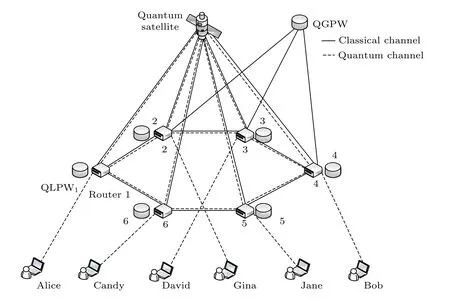
圖10 基于蛛網拓撲的量子衛星廣域網Fig. 10. Quantum satellite wide area network based on cobweb topology.

假設源節點Alice要給目的節點Bob發送信息, 初始Alice先給Router1發送一個請求, 即將量子信息發送給Bob, 然后Router1通過QGPW查詢自己的位置信息, 識別Bob在哪個基站下面,QGPW的優點在于可以找到符合網絡的最短路徑路由, 使信息高效傳輸. 由圖10可知網絡中只有一個量子衛星, 通過QGPW可以查詢到Alice和Bob在同一顆衛星下, 此時QGPW會通知Router1的目的用戶Bob的具體位置, 同時在通信的過程中, Router1請求quantum satellite發送糾纏光子對給相應的基站, 建立起衛星與基站之間的量子信道, 利用N階量子隱形傳態路由方案有效傳送Alice所要傳送給Bob的信息.

5 基于N階量子隱形傳態的量子衛星廣域網性能仿真

5.1 量子信息傳輸誤碼率分析

由于存在環境噪聲、人為干擾等因素會導致通信鏈路失效, 使糾纏粒子的狀態發生變化, 從而產生錯誤的傳輸. 設量子信息傳輸誤碼率為Pr[9], 公式為

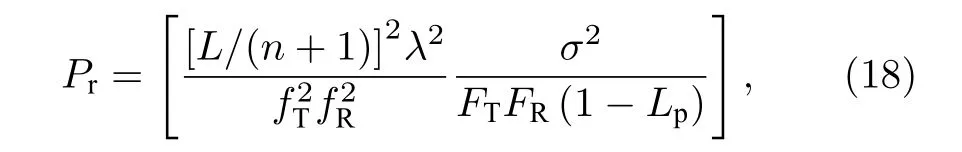
式中σ2是噪聲平均功率譜密度, 其余各參量的含義如表3所列.

表3 量子信息傳輸誤碼率各參量含義Table 3. Meaning of parameters of bit error rate in quantum information transmission.

為了減小大氣環境對傳輸鏈路產生的衰減效應, 應該選擇合適的光波長, 根據文獻[21], 應選擇透射率較高的大氣窗口, 因此本文取λ=1550nm進行分析. 其余參數設置為n=0 ,fT=fR=32mm ,FT=FR=1,Lp=5% , 噪聲的平均功率譜密度分別為1, 2和3 dB/km.

首先分析在無中繼節點的情況下, 誤碼率Pr與傳輸距離L之間的關系. 仿真結果如圖11所示.

當σ2一定時, 星地之間傳輸距離越大, 誤碼率越大. 在σ2=1dB/km 條件下, 當傳輸距離為2000 km時, 誤碼率為0.049; 當傳輸距離為4000 km時, 誤碼率達到0.197. 在量子信息在星地之間的傳輸距離一定的條件下,σ2越大, 誤碼率也越大,當 傳 輸 距 離 為3000 km,σ2=1dB/km 時 誤 碼 率為0.111;σ2=3dB/km 時誤碼率達到0.332. 因此在沒有中繼的情況下, 傳輸更遠距離時誤碼率增大, 就需要考慮引入中繼.

當星地之間的傳輸距離L為4000 km時, 分析功率譜密度σ2、中繼節點個數n與誤碼率Pr的關系, 仿真結果如圖12所示, 誤碼率的其余參量取值同圖11.

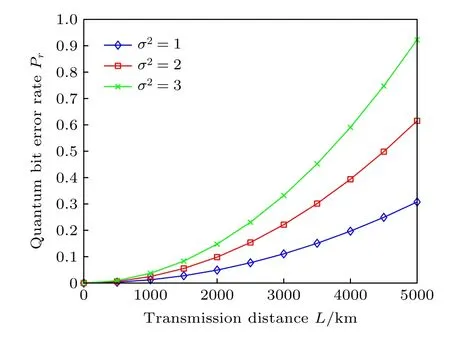
圖11 誤碼率與傳輸距離的關系Fig. 11. Relationship between BER and transmission distance.

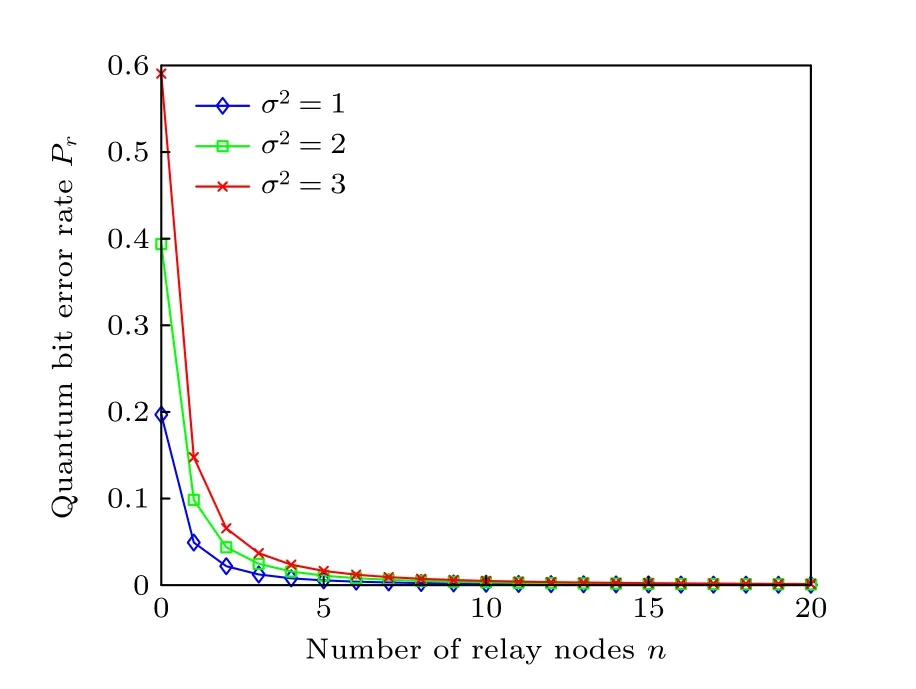
圖12 誤碼率與中繼節點個數的關系Fig. 12. Relationship between bit error rate and the number of relay nodes.

當σ2一定時, 誤碼率隨著n的增大而減小, 當中繼節點數取為6或者更大時, 誤碼率幾乎保持不變, 因此在量子衛星廣域網中進行信息傳輸時要選擇合適的路由過程, 使得信息有效傳輸.

5.2 量子廣域網吞吐率分析

基于N階量子隱形傳態的量子衛星廣域網中,設成功分發糾纏光子對的概率為P1、在QGPW中成功查找位置信息的概率為P2、成功進行量子門操作的概率為P3、接收端成功接收量子信息的概率為P4. 那么成功將一個量子態信息傳輸至目的節點的概率為

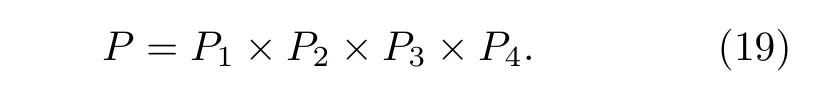
在N階量子隱形傳態的過程中, 生成糾纏粒子對的時間為h、在位置數據庫中查找信息的時間為w、進行量子門操作的時間為j、在中繼節點處的傳輸時延為T′′. 而在N階量子隱形傳態的過程中, 傳輸一個量子態的時間不會隨著中繼節點個數的增多而增大,T1是量子隱形傳態的平均時間,所以

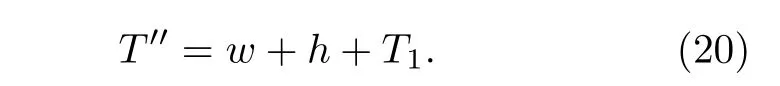
因此成功傳輸一個量子態所需要的時間為

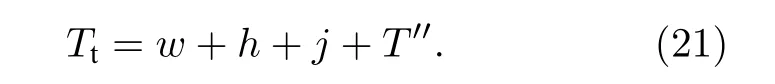
則在量子衛星廣域網中傳輸量子信息時網絡吞吐率可以定義為

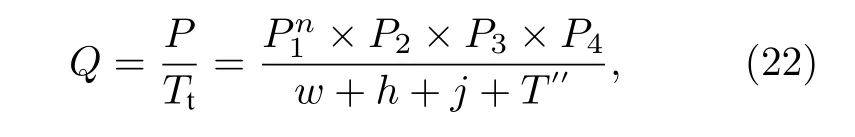
其中w,h,j的大小相比于T′′很小, 可以忽略不計,所以

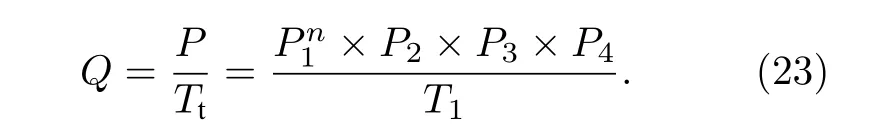
令T1=0.8μs , 分析吞吐率Q與P1,n的關系.根據文獻[22]可知, 在理想條件下概率均設為0.8, 所以令P2,P3,P4均為0.8, 仿真結果如圖13所示.

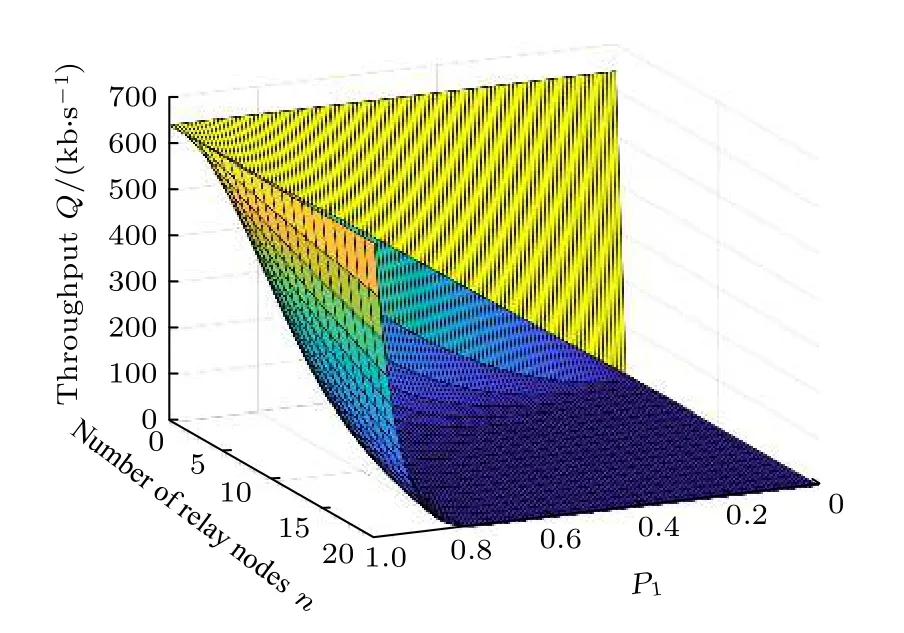
圖13 吞吐率Q與 P 1 以及中繼節點個數n的關系Fig. 13. Relationship between throughput rate Q and P1 and the number of relay nodes n.

由仿真結果可知, 在傳輸時延不變的條件下,隨著P1的增大, 吞吐率Q也在逐漸增加, 最大可以達到640 kb/s; 隨著中繼節點個數n的增大,吞吐率逐漸降低. 因此在蛛網拓撲結構下, 要選擇合適的路由過程使得量子信息的吞吐率盡可能大.

令P1=P2=P3=P4=0.8 時, 分析吞吐率Q與傳輸時延Tt的關系, 其中中繼節點個數分別取2, 4, 6, 仿真結果如圖14所示.

圖14 吞吐率與傳輸時延的關系Fig. 14. Relationship between throughput Q and transmission delay.

隨著網絡中傳輸時延的增大, 吞吐率Q逐漸減小. 但在N階量子隱形傳態路由方案下, 傳輸時延基本不變, 且在蛛網網絡拓撲下可選路徑多, 傳輸時延小, 因此本文提出的基于N階量子隱形傳態的蛛網網絡拓撲量子廣域網的吞吐率不會隨著傳輸時延的增大有明顯的降低.

5.3 安全密鑰生成率分析

網絡的安全性主要是指在一定鏈路條件下所能獲得的最高安全密鑰生成率. 在量子衛星廣域網通信過程中, 進行量子信息傳輸時僅考慮理想的單光子源, 在單個脈沖中含u個光子的概率為[23]

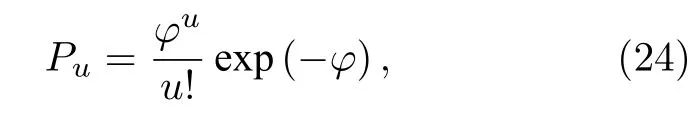
式中φ為平均光子數, 在一般的量子通信實驗中,φ取值為0.1[23], 來獲取準單光子源. 根據誘騙態方案, 可知單光子的計數率為

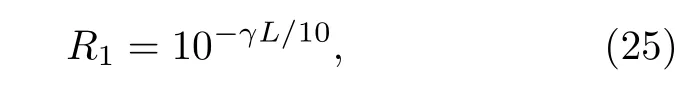
式中γ為量子信道衰減系數, 通常取值為0.2 dB/km,L為量子信息的傳輸距離. 考慮單光子計數率后,可以得到安全密鑰生成率為

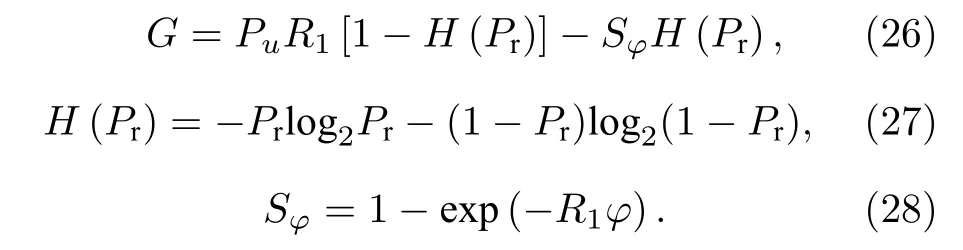
根據(18)式、(27)式和(28)式可知, 影響密鑰生成率的參數主要為量子信息的傳輸距離L, 中繼節點個數n, 噪聲平均功率譜密度σ2.

1) 在不考慮中繼的情況下, 仿真分析密鑰生成率與傳輸距離的關系, 仿真結果如圖15所示.當σ2取3 dB/km, 傳輸距離L= 2500 km時, 密鑰生成率為0.023 bit/s; 傳輸距離為L= 4000 km,密鑰生成率減小至0.008 bit/s, 因此當量子信息的傳輸距離增大時, 網絡誤碼率增大, 從而導致安全密鑰生成率逐漸減小.

圖15 密鑰生成率與傳輸距離的關系Fig. 15. Relationship between key generation rate and transmission distance.

2) 由上述結果可知, 隨著密鑰生成率的降低要考慮引入中繼. 當量子信息的傳輸距離為3500 km時, 仿真得到網絡密鑰生成率與n的關系如圖16所示, 隨著n的不斷增大, 密鑰生成率增加, 在蛛網網絡拓撲結構中, 任意兩個節點之間的通信路徑不止一條, 迂回路由多, 可以在網絡中選擇合適的中繼節點個數, 找到最優路徑, 使得網絡的密鑰生成率達到最大, 網絡安全性更高.

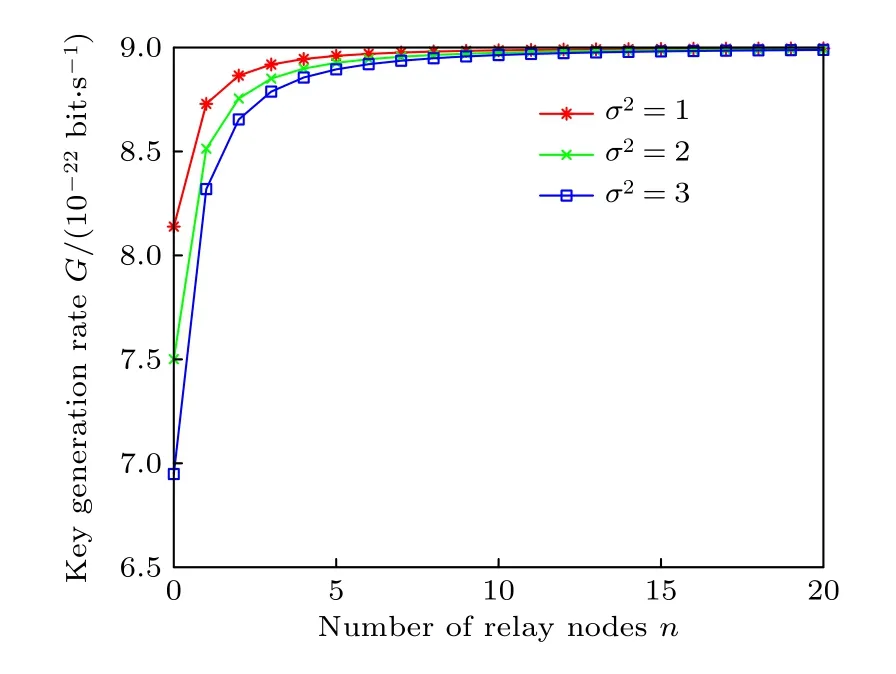
圖16 密鑰生成率與中繼節點個數的關系Fig. 16. Relationship between key generation rate and number of relay nodes.

綜上, 對網絡安全密鑰生成率的仿真實驗可知, 本文提出的基于蛛網拓撲的量子衛星廣域網中繼傳輸模型, 一定程度上改進了信息傳輸的安全性問題, 保證了量子信息通過中繼節點傳輸時的安全性.

6 結 論

本文利用蛛網網絡拓撲構建量子衛星廣域網,SNT具有高可靠性, 且N階量子隱形傳態路由方案的傳輸時延小. 增加中繼節點數可以有效降低網絡的誤碼率, 增大量子衛星成功分發糾纏光子對的概率可以提升網絡吞吐率, 雖然吞吐率會隨著傳輸時延的增大而減小, 但在該路由方案下傳輸時延基本不變, 且SNT的傳輸時延小, 所以量子衛星廣域網的吞吐率不會有明顯的降低, 且其在一定程度上改進了信息傳輸的安全性. 因此采用該路由方案以及蛛網網絡拓撲構建量子衛星廣域網可靠性高、誤碼率低、吞吐率大, 這為建立全球范圍的量子衛星廣域網奠定了理論基礎.