基于高中數學基本不等式解題技巧分析
李光星
(山東省新泰市第一中學 271200)
鑒于高中數學的實踐性特征十分強,并且很多數學知識均存在著明顯的規律性特點,邏輯性非常高.在高中數學教學中,需不斷改進不等式解題教學方式.具體實施不等式教學時,假如學生們無法深入理解,熟練掌握不等式的解題方法和技巧,必然會影響到解題的速度和準確性.為了改變此種不良的情況,教師需要加強對學生傳授不等式的解題技巧,讓學生學習到更多的知識.鑒于此,系統思考和分析高中數學基本不等式解題技巧顯得尤為必要.
一、基本不等式概念的闡釋
一般來說,可以應用基本不等式求解函數的最值,亦或者完成證明,并利用具體的文字加以體現,主要針對的是兩個正實數的算數平均數大于或者等于它們的幾何平均數.顯而易見,不等式知識的學習屬于高中數學教學過程當中的難點部分,常見于高考數學試卷當中,所以要求學生們靈活掌握基本不等式的解題方法和技巧.
二、高中數學基本不等式解題技巧的說明
1.科學利用基本不等式相關性質進行習題的求解
一般來說,高中數學教師為學生們講解與分析基本不等式習題求解方法的時候,需要科學利用基本不等式相關性質,完成求解的任務.作為一種常用的基本不等式解題方法,對于很多不同類別的不等式習題而言,均可以采用此種解題方式.比如,可以利用不等式的傳遞性質,假如a>b,b>c,說明a>c.與此同時,由不等式的可加性得出a+c>b+c.例如:教師講解新教材人教A版高中數學《基本不等式》為學生們設計了如下問題:
例1已知平面上有n個圓,其中每兩個圓都相交于兩點,每三個圓不相交于同一個點.證明:n個圓把平面分成f(n)=n2-n+2個部分.
分析證明f(n)=n2-n+2公式成立時,主要運用了歸納方法.在n=1的情況下,f(1)=2,即n2-n+2=2成立,所以,該命題成立.與此同時,假設n=k,并且第k+1個圓的圓心用O代表,聯系題目相關條件,以便完成證明的任務.借助上述各種方法,都能夠證明f(n)=n2-n+2是成立的.在此過程當中,通過利用基本不等式的相關性質,能夠減小基本不等式習題的求解難度.所以說,得出最終的準確證明結果是非常關鍵的,擁有一定的實踐意義和價值.
2.指導學生熟練掌握不等式的相關基礎知識,提升不等式解題的準確率
一直以來,基本不等式對于高中學生而言,屬于難點內容之一,很多數學基礎弱的學生,在學習的過程當中覺得十分吃力,非常容易產生不同方面的問題和缺陷.為了改變此種不良的情況,要求高中數學教師應該重視夯實學生的不等式基礎知識,有助于學生們做到溫故知新,提高學生基本不等式習題的解題準確率.教師進行高中數學基本不等式的教學時,需要為學生們講授基本不等式和幾何性質之間的聯系,引導學生們深入掌握基本不等式成立需要的相關條件,達到拓展知識的效果.當學生進行基本不等式解題時,可以使用湊項、消元等方式,這也是學生必需掌握的解題方法,要求學生靈活使用,以便完成求解不等式的學習任務.例如:教師講解新教材人教A版高中數學《基本不等式》,為學生們設計了如下問題:
例2(1)如果正數x,y滿足x+3y=5xy,則3x+4y的最小值是____;
(2)如果x>0,y>0,x+3y+xy=9,則x+3y的最小值是____.
分析求解問題(1)的時候,學生們可以合理運用基本不等式相關知識,便能夠實現.針對問題(2)的求解來說,存在著一定的難度.在此過程當中,數學教師可以指導學生們使用消元的方式加以求解.
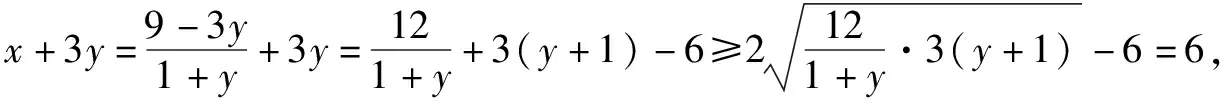
3.加大基本不等式換元解題技巧的應用力度
教師指導學生們進行不等式習題分析和探究時,能夠把式子視為一個整體,并運用變量予以替換,以便使不等式解題十分便捷,這種解不等式的方法也叫做換元法,達到了有效轉化不等式的目的.在此環節當中,應該加大對置換元、構建元等相關要素的關注力度.實際上,對于換元法而言,可以采用等量代換的方式,實現不斷地延伸,并且在此過程當中,能夠不斷變換具體的研究目標,進而完成轉移問題的任務.與此同時,還能夠運用換元法,將新的變量融入到不等式中,進而實現科學處理相關分散條件的目的,把那些隱藏的相應條件有效體現出來.亦或在進行不等式解題分析的過程中,可以把結論和相關條件有效融合到一起,以便形成學生們更加熟悉的結構,讓后續的不等式解題變得更加簡便、高效.例如:教師講解新教材人教A版高中數學《基本不等式》時,為學生們設計了如下問題:
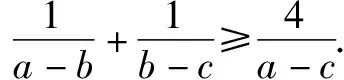
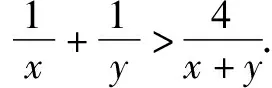
4.確保不等式反證解題技巧運用的合理性
學生求解不等式習題時,教師可以教會學生運用反證解題技巧完成求解的任務.一般地,這種解題技巧的利用以正難則反作為重要的前提條件,將其應用到高中數學不等式的求解與證明當中,能夠得到一定的成效.通過運用這種不等式解題技巧,可以完成解決有關不等式方面的問題,并且,能夠提升不等式解題的準確率.例如:教師講解新教材人教A版高中數學《基本不等式》相關課程內容的過程當中,為學生們設計了如下問題:
例4已知a+b+c>0,abc>0,ad+bc+ac>0,求證:a>0,b>0,c>0.
分析進行求解以前,應該細致分析題目中的已知條件.因為abc>0,所以a,b,c都不等于0.假如a<0,bc<0,符合相關條件的a+b+c>0,并且b+c>-a,得到a(b+c)<0.因為ab+bc+ac=a(b+c)+bc<0,所以該結果和題目中的條件形成矛盾,所以以上假設是不成立的.即a>0,b>0,c>0.由此達到證明的目的.
從以上分析中不難看出,系統分析與思考高中數學基本不等式解題技巧顯得尤為必要,具有一定的研究意義和實施價值.希望此次研究能夠得到有關高中數學教師的關注與重視,并且從中獲取到相應的借鑒和幫助,以便增強高中數學基本不等式解題技巧應用的實際成效,進而促進我國高中數學教育事業的可持續發展與進步.

