借助模型法 解答物理難題
張 圖
(四川省南充高級中學 637000)
物理涵蓋很多的模型,主要有等時圓模型、渡河模型、拋體模型等.教學中既要為學生認真細致的講解這些模型,使其掌握模型中物體的運動規律與特點,深刻理解模型內涵,又要結合具體例題講解,為學生運用模型解題做好示范,使其真正掌握,靈活應用.
一、借助等時圓模型解題
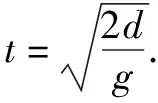
例1如圖1所示,一傾角為θ的斜面上方A點放置一光滑木板AB,B端剛好在斜面上.木板與豎直方向AC所成的角為α.一物塊由A端沿木板由靜止下滑,要使物塊滑到現斜面的時間最短,則α和θ的關系為( ).
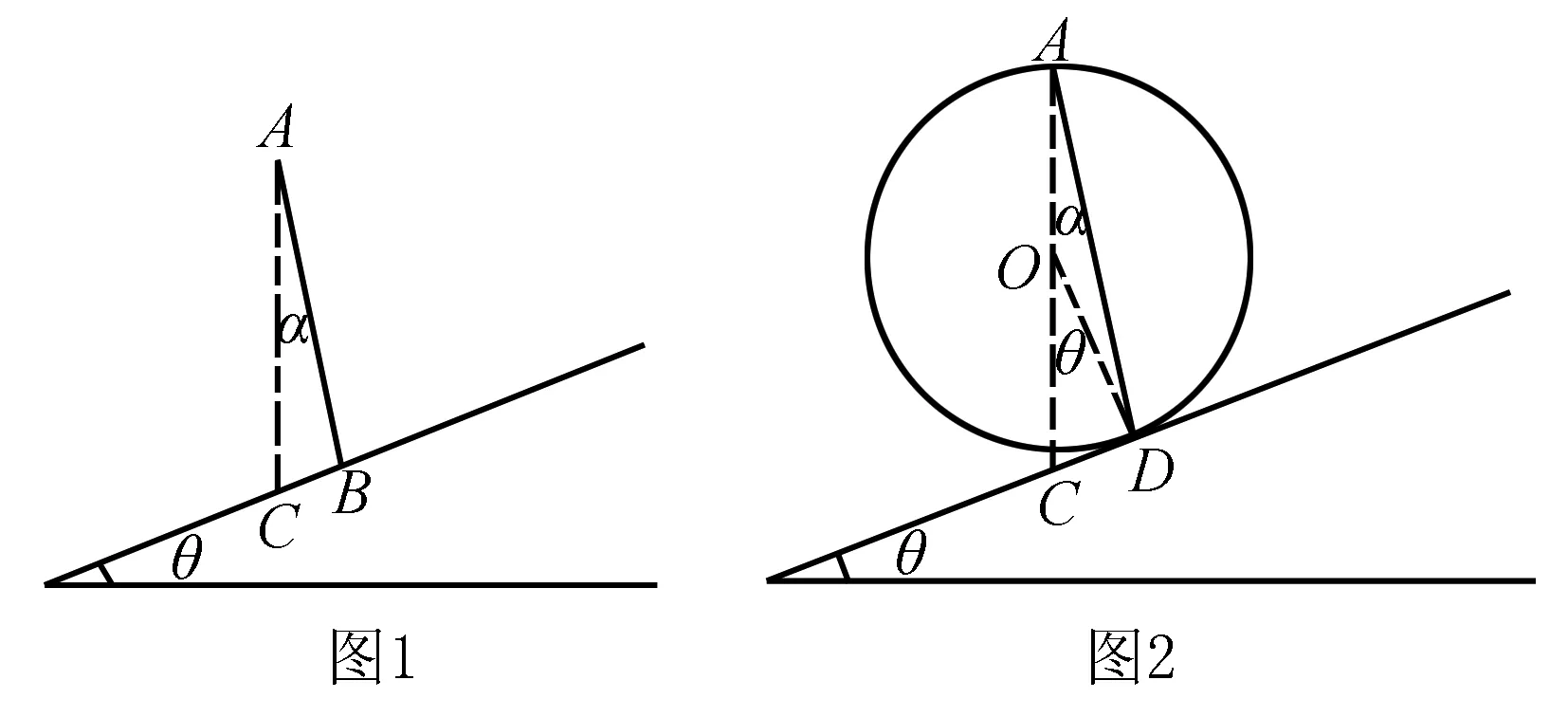
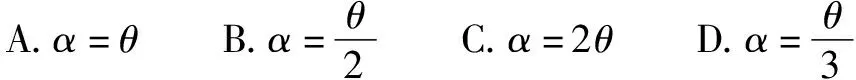
題目創設的情景較為新穎,很多學生審題后不知如何下手,究其原因在于其遷移所學知識的能力較差.該題目考查學生運用等時圓模型解題的靈活性.解答該題的關鍵在于結合題干中的情景構建合適位置的等時圓,課堂上可給予學生啟發,使其盡快找到解題思路.
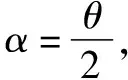
二、借助渡河模型解題
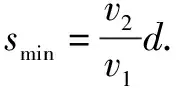
例2某人劃船橫渡一條河,河水流速處處相同且恒定,船的劃行速度恒定.已知此人過河最短時間為T1;若此人用最短的位移過河則需時間為T2.已知船的劃行速度大于水速,則船的劃行速率與水流速率之比為( ).
該題目涉及船渡河時的兩種情境,只有深刻理解模型,才能順利解題.解題中應設出合理參數,借助模型直接求出渡河最短時間的表達式.在探討船的最短位移時引導學生繪制相關的草圖,聯系所學模型,找到速度之間的關系.
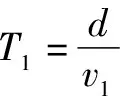
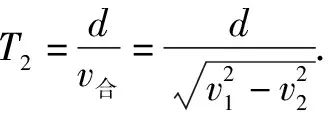
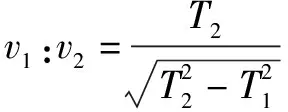
正確選項為A.
三、借助拋體模型解題
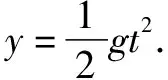
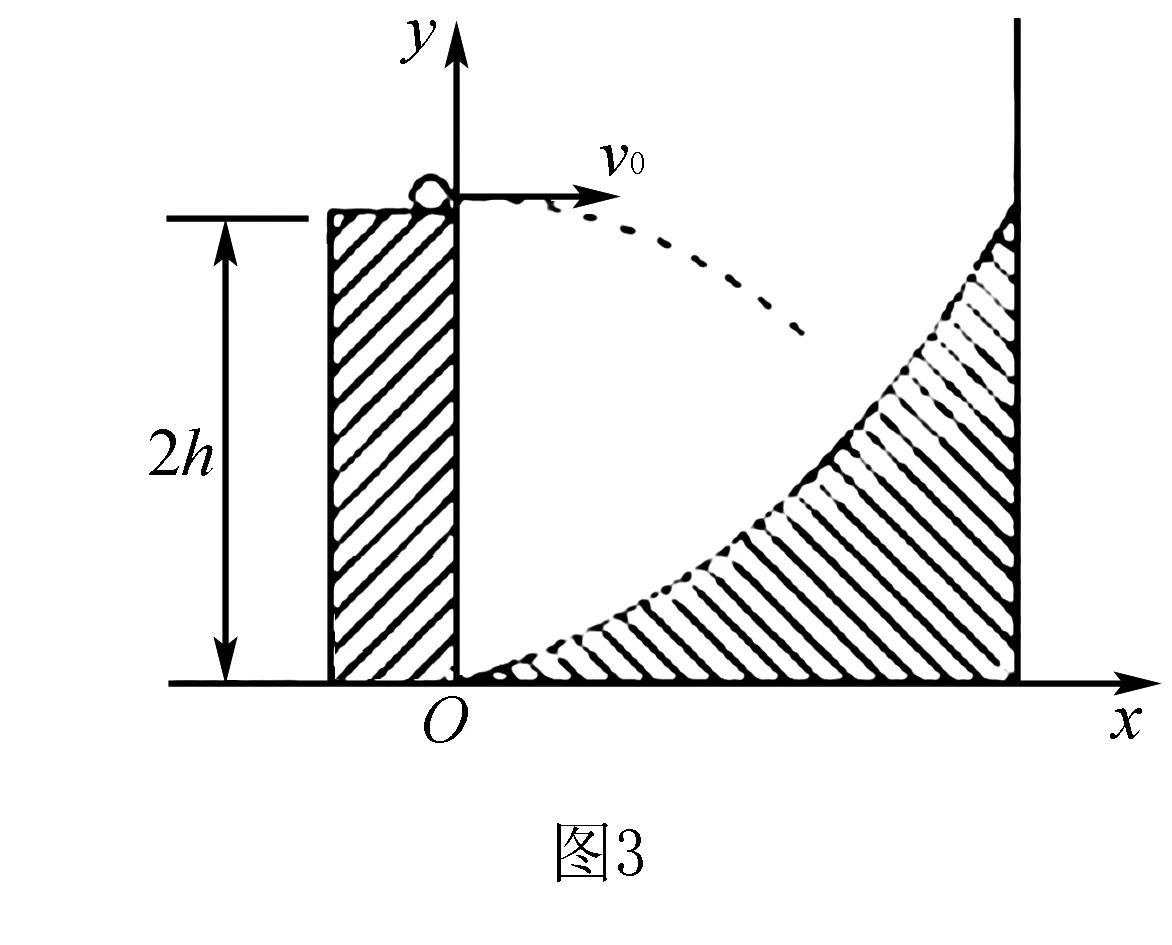
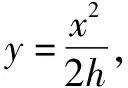
該題目創設的情境并不復雜,但卻涵蓋很多知識,主要有拋體模型、動能定理以及數學知識等.教學中要求學生認真審題,積極回顧所學的拋體模型,建立相關的方程,表示出Ek,而后運用數學知識求其最小值.
設探險隊員跳到平面上時的水平位移為x,豎直位移為H.
由幾何關系可得y=2h-H,
由數學知識得到
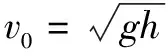
高中物理教學中注重相關模型的講解對提高學生的解題能力具有重要的促進作用,因此,應結合教學進度靈活采用多種方法,做好物理模型教學工作,尤其應創設具有難度的試題,訓練學生運用模型解題的技能,促進其解題水平與能力的進一步提升.

