圓錐曲線中最值問題的求解策略

鄒慶龍

(福建省長汀縣第二中學 366300)

一、均值不等式法

均值不等式法是高中數學的一個重要公式：a2+b2≥2ab，當且僅當a=b時，等號成立.在圓錐曲線最值的求解中，均值不等式常用于離心率的計算，題干中已知離心率，求離心率之差或之和，通過共軛方程的設立，分別表示離心率，然后利用均值不等式a2+b2≥2ab的原理，求得最值.

例1一對共軛曲線的離心率分別為e1,e2，求e1+e2的最小值.

解析設這對共軛曲線的方程為：

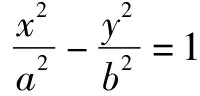
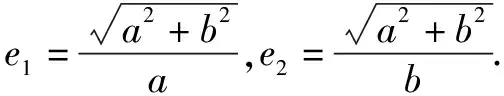
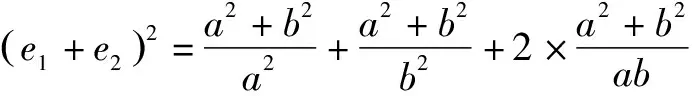
≥2+2+2×2

=8.

所以當且僅當a=b時，等號成立.

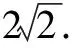
二、參數法

參數法是指在解題過程中，通過適當引入一些與題目研究的數學對象發生聯系的新變量(參數),以此作為媒介,再進行分析和綜合,從而解決問題.在求圓錐曲線上點到直線的問題中，可以利用圓錐曲線的參數方程的定義，將點P用參數式表示出來，然后將點到直線的距離表達出來，根據三角函數的性質得到直線的最短距離，同時得到sinθ和cosθ值，即點P的坐標.

解析設點P到l的距離為d，

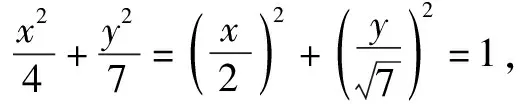
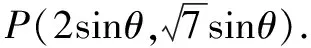
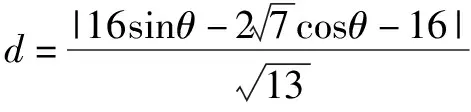
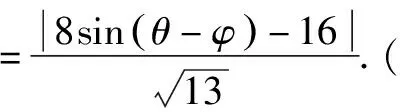
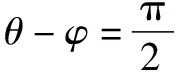
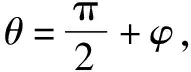
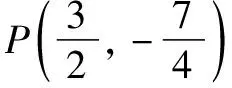
三、判別式法

判別式法可以判斷方程是否有根以及有幾個根，b2-4ac<0無實數根，b2-4ac=0有兩個相等實數根，即一個實數根，b2-4ac>0有兩個不相等實數根.在圓錐曲線最值求解中，若求函數式，則需構建等式，化簡得出y的表達式，聯立已知橢圓的方程與構建的新方程，利用判別式原理得出新方程的值.

例3已知(x,y)是橢圓x2+4y2=1上的點，試求3x+4y的最大值與最小值.

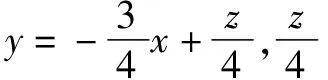
解析設3x+4y=z,

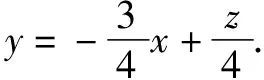
13x2-6zx+z2-4=0.

所以根據判別式Δ=b2-4ac，

得Δ=36z2-4×13(z2-4)≥0.

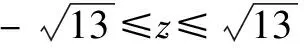
圓錐曲線最值求解是數學學習的重點內容，也是高考出題考慮的范圍，其涉及的知識繁多，可應用的方法也是多樣化.通過均值不等式法、參數法和判別式法三種方法的理解，同學們要加強核心內容的練習，熟練運用，加深對圓錐曲線內容的深化.