面向STL文件的截面輪廓線段連接方法研究

文 豪，高 健，張正甫

（1.廣東科學技術職業學院機械與汽車學院，廣東 珠海 519090；2.廣東工業大學機電工程學院，廣東 廣州 510006）

1 引言

在計算機中，STL的文件格式[1]可用于表示三維模型的外形尺寸，常用于逆向工程、快速原型、快速制造等相關工業領域[2]。其中針對3D打印及快速原型等應用環境，STL文件經常需要進行輪廓切片及截面求交的數據處理操作。對此，可行的計算機數據處理操作為先判斷網格面片與截平面的位置關系并提取相交面片的幾何信息[3]，再依次計算相交截點的坐標信息并連接形成截面輪廓[4]。

然而，STL的文件格式[5]僅隨機記錄三維模型的網格面片信息，并且只包含面片法矢與三個頂點的三維坐標。STL文件的模型數據無法直接實現截面交點的相鄰關系位置判斷，需要在模型的切片操作前對STL文件進行拓撲重構的數據處理操作，建立多種模型幾何數據的直接映射關系[6]。文獻[7]提出了基于標準模板庫set容器的拓撲關系重建算法，可有效去除STL文件的冗余數據，實現了模型數據的快速切片操作。文獻[8]根據模型的冗余信息確定了三角面片之間的拓撲關系，并判定有序點列形成封閉的截面輪廓。文獻[9]使用半邊數據結構重構了三角面片間的鄰接拓撲關系，解決了截面輪廓生成中截面交點的有序連接問題。基于ACIS平臺，文獻[10]研究了STL模型的拓撲重構問題，實現了模型數據快速準確的算法操作。文獻[11]使用三維k-d樹的方法實現了網格模型的自適應分層切片，并在增材制造中實際應用。文獻[12]提出了基于鏈表的拓撲重建算法，可有效提高切片算法的整體效率。文獻[13]以哈希表作為查找表，建立了模型的幾何拓撲關系，可顯著提升后續的切片效率。文獻[14]提出了STL文件的數據擴展格式，豐富了模型文件內容，可實現切片數據的直接生成。

綜上所述，針對3D打印中模型數據的截面輪廓求取問題，目前研究先對模型文件進行幾何拓撲數據重構，再在已知幾何鄰接關系的基礎上依次求取表示截面輪廓的交點坐標，從而根據模型重構的幾何拓撲關系連接截面交點生成截面輪廓。然而模型文件的幾何拓撲數據重構操作復雜，常伴隨著大量的冗余數據處理，嚴重影響3D 打印系統中的截面輪廓與加工路徑生成速度。對此重點研究STL文件的截面求交操作與輪廓線段的連接方法，通過STL文件的計算機數據格式特征分析，提出了面向STL文件的截面輪廓線段連接算法，先通過截面與面片的相交判斷與交點計算，獲取所有的相交輪廓線段，再對相交輪廓線段的鄰接關系進行判斷，最終形成有效的截面輪廓，并于PythonOCC的測試平臺中編程驗證。該算法可直接避免模型數據的拓撲數據操作，通過STL文件的直接數據處理，直接實現3D打印中模型數據截面輪廓的獲取生成。

2 STL文件的數據處理分析

區別于工程領域中的參數化模型，三角網格模型使用一系列三角面片表示模型的外形輪廓。在計算機中常以STL的文件格式存儲模型數據，其中隨機記錄了三維模型的網格面片信息。STL文件中的一個面片數據只包含面片法矢與三個頂點的三維坐標，如圖1所示。

圖1 STL文件中的一個面片數據Fig.1 One Facet Data in STL File

在模型數據的獲取與處理當中，三角網格模型可能存在著幾何缺陷問題，包括共邊、相交、重疊、孔洞裂縫等[15]，會造成截面輪廓的求交計算錯誤。然而STL文件中并未直接反映這些幾何缺陷問題，在截面輪廓的生成計算前應優化模型文件，確保網格質量。對于正確有效的模型數據，算法生成的截面輪廓應為首尾相連、不重疊重復的有序線段，且每條輪廓線段對應一個面片，如圖2所示。

圖2 STL文件的截面輪廓線段Fig.2 Cross Contour Segments of STL File

目前研究的操作過程為先對STL文件進行模型數據的幾何關系拓撲重構，建立幾何數據的映射關系，再在此基礎上計算截面交點的坐標數據，并根據模型重構的幾何拓撲關系連接截面交點生成截面輪廓。然而拓撲重構的數據處理量大，并伴隨著與當前截面求交無關的大量冗余數據操作，對于STL文件的直接截面輪廓生成操作不具備速度優勢。另一方面，由于截面輪廓線段分別對應于網格模型的相交三角面片，其數據信息已于STL文件中逐一記錄。因此，針對STL文件的截面輪廓生成操作，應直接處理STL文件的模型數據。

3 算法原理與操作步驟

所提算法的主要思路是利用STL文件逐次記錄的面片信息直接計算截面輪廓線段，再直接判斷各線段的鄰接關系生成截面輪廓，無需依靠模型重構的幾何拓撲關系判斷截面交點的連接順序。算法流程，如圖3所示。其中可分為三步操作。

圖3 算法流程Fig.3 Algorithm Flow

3.1 相交面片判斷與數據選取

欲使模型輪廓與截平面求交，則截面不能與輪廓重合，面片與截面只有相交和不相交的兩種位置關系。若面片與截面不相交，則面片三個頂點均位于截面的一側，可利用該特征依次提取STL文件中的面片數據，再判斷是否與截面相交，如圖4所示。

圖4 截面與面片不相交的情況Fig.4 Situation that Cross Section and Facet are not Intersect

截平面的空間坐標表達式均可轉換為一般方程：

式中：A、B、C、D—已知常數，A、B、C不可同時為0。設頂點與截面的位置判斷函數：

對于提取的一個網格面片數據，可將三個頂點v1、v2、v3的三維坐標分別代入式（2），若f(x，y，z)的三個計算值均大于或小于0，說明了面片的三個頂點均位于截面的一側，面片與截面不相交。否則應選取當前面片數據，并用于下一步的算法處理操作。

3.2 截面輪廓線段的計算生成

截面與面片相交可劃分為四種情況，如圖5所示。其中，相交的結果均可表示為一段長度大于或等于0的直線線段，并可用兩個頂點的三維坐標表示。

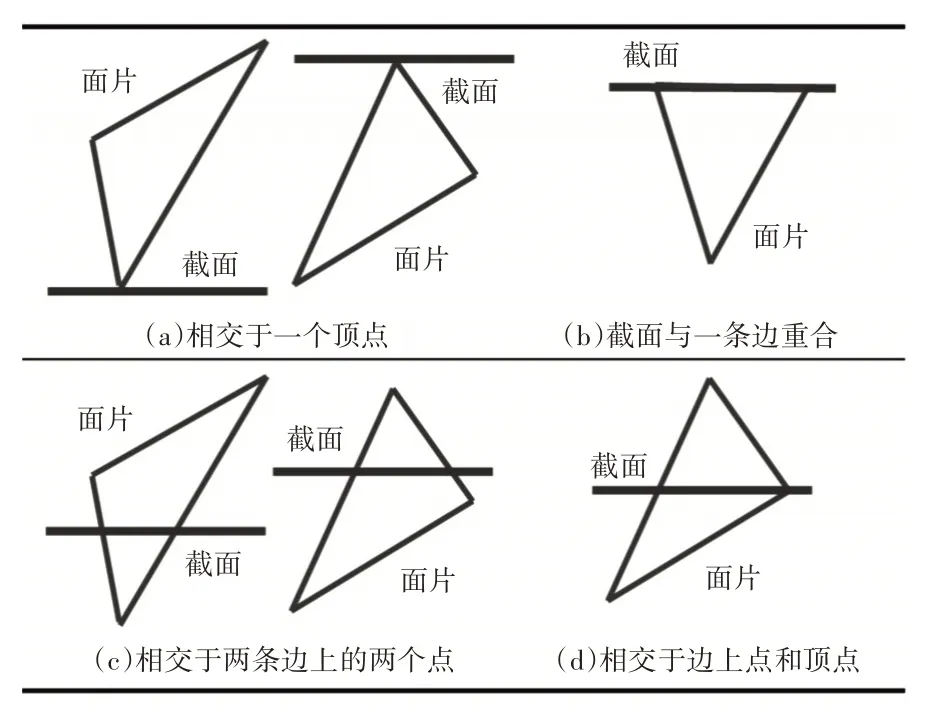
圖5 截面與面片相交的四種情況Fig.5 Four Situations of Cross Section and Facet

輪廓線段兩個頂點的三維坐標計算判斷如下：

（1）若面片三個頂點的f(x，y，z)計算值有兩個為0，則截面與一條邊重合，輪廓線段的兩個頂點即為f(x，y，z)計算值為0的兩個面片頂點。

（2）若面片三個頂點的f(x，y，z)計算值有且僅有一個為0，則需判斷另外兩個面片頂點相對截面的位置關系。若另外兩個面片頂點的f(x，y，z)計算值均大于或小于0，則說明了面片與截面相交于一個頂點，輪廓線段的長度為0，兩個頂點均為f(x，y，z)計算值為0的面片頂點。若另外兩個面片頂點的f(x，y，z)計算值出現一個大于0和另一個小于0的情況，則說明了面片與截面相交于邊上點與頂點。此時輪廓線段的一個頂點為f(x，y，z)計算值為0的面片頂點，另一個頂點為面片邊與截面交點，需要選取f(x，y，z)計算值不為0的兩個面片點與截面方程聯合求解。

（3）若面片三個頂點的f(x，y，z)計算值均不為0，則面片與截面相交于兩條邊上的兩個點。截面與邊相交，邊的兩個頂點也應分別位于截面兩側。從面片三個頂點中選取兩組f(x，y，z)計算值分別大于0和小于0的兩個面片頂點組成兩條面片邊，再分別與截面方程聯合求解，可得輪廓線段兩個頂點的坐標數據。

截面與面片邊的交點計算，如圖6所示。根據截面方程和兩個分別位于截面兩側的面片頂點可實現交點坐標的聯合求解。

圖6 截面交點的求解計算Fig.6 Calculation of Cross Section Intersection

相交邊的兩個頂點與坐標為P1(x1，y1，z1)和P2(x2，y2，z2)，分別位于截面的兩側，與截面的距離分別為d1和d2，可通過點到面的距離公式計算：

設截面交點及坐標為P(x，y，z)，根據點與點的距離比例關系，可得截面交點P的x坐標函數關系：

至此，通過對所有相交面片的求交計算，可生成所有的截面輪廓線段，且每段線段包含兩頂點的坐標信息。然而選取STL文件的相交面片順序是隨機的，計算生成的截面輪廓線段也是隨機無序的，需要對輪廓線段的相同頂點進行判斷及連接才能生成截面輪廓。

3.3 截面輪廓線段的判斷連接

對于不同的模型外形輪廓特征，截面輪廓是各不相同的。對于無幾何缺陷問題的STL 文件，其模型外形可劃分為封閉曲面、開放曲面及組合曲面三類，如圖7所示。其中，封閉曲面的截面輪廓為首尾相連的閉合線條；開放曲面的截面輪廓為首尾不連接的線條；組合曲面則為多個曲面的組合，其截面輪廓也為多個單一截面輪廓的組合，各截面輪廓之間互不相同。

圖7 截面輪廓的分類Fig.7 Classification of Cross Contour

根據上述的相交面片判斷與數據選取及截面輪廓線段計算生成操作，可以得到當前截面所對應的輪廓線段，每條輪廓線段則包含兩個頂點的坐標信息，且截面輪廓線段的所有數據均為無序排列。對網格模型的截面輪廓線段進行了歸類劃分，如圖8所示。其中單一截面輪廓可能存在封閉與開放的兩種情況，組合截面輪廓則由多個單一截面輪廓組成。

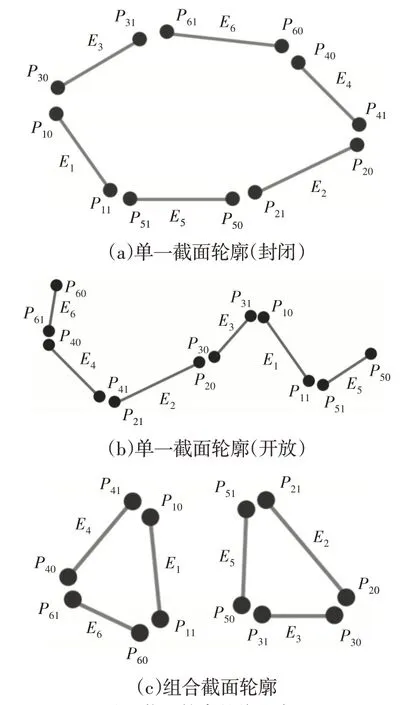
圖8 截面輪廓的線段類型Fig.8 Segments Types of Cross Contour

對于截面輪廓的最終生成，需要對無序的輪廓線段進行連接，判斷單一截面輪廓的封閉性，并分別存儲組合截面輪廓中各個單一截面輪廓的數據信息。結合圖8，具體的算法步驟及描述如下：

（1）選取輪廓線段的任意頂點作為起點。可任意選取P40作為起點，如圖8（a）所示。

（2）使用當前選定的頂點檢索相鄰輪廓線段。由于截面交點計算可能存在一定的精度損失，若某個輪廓線段頂點與該頂點的距離小于允許計算精度（建議值為0.0001mm），則可認為兩頂點所對應的兩條截面輪廓線段相鄰。如依次計算其他輪廓線段的頂點與已選取頂點P40的距離，其中，唯有P60符合允許計算精度要求。因而可知頂點P40和P60對應的截面輪廓線段E4和E6相鄰，公用頂點坐標為P40和P60的坐標平均。

（3）使用上述操作（2）的方法依次檢索相鄰輪廓線段，獲取最終輪廓連線的頂點坐標。通過已檢索的頂點P60及其對應的輪廓線段E6可快速獲取另一頂點P61，再使用（2）的方法可依次檢索P61→P31→E3→P30→P10→E1→P11→...，最終生成的截面輪廓為相鄰輪廓線段公用頂點的依次連線，即

（4）判斷當前生成截面輪廓的封閉性。對于上述的操作（3），在相鄰輪廓線段數據信息的依次檢索中，可能出現封閉輪廓的重復檢索問題，也可能出現開放輪廓無法繼續檢索的問題。對于封閉輪廓的判斷，可將相鄰輪廓線段快速獲取的另一頂點與起點相比較，若為同一頂點則封閉輪廓形成閉環。每次相鄰輪廓線段快速獲取的另一頂點P61、P30、P11等均與起點P40比較，直至頂點P41對應輪廓線段E4快速獲取的另一頂點為起點P40，如圖8（a）所示。對于開放輪廓的判斷與處理，若沒有任何頂點與選定頂點的距離小于允許計算精度，則說明該選定頂點為邊界點，此時應返回起點并使用操作（2）的方法向另一個方向檢索相鄰輪廓線段直至邊界點。若從起點檢索至P50，無法檢索下一相鄰輪廓線段，P50為邊界點，返回起點并沿另一方向檢索，直至另一邊界點P60為止，如圖8（b）所示。

（5）組合截面輪廓的判斷與處理。若通過上述的4步操作仍有未被檢索的輪廓線段，說明該截面輪廓為組合的，并存在未被處理的單一截面輪廓。可將未被檢索的輪廓線段重新用于上述的4步操作，生成另一個單一截面輪廓，直至所有的輪廓線段均被檢索。若E1、E4、E6所組成的單一截面輪廓已被處理，剩下的E2、E5、E3未被檢索，可使用上述的4步操作生成對應的另一個單一截面輪廓，從而形成最終完整的組合截面輪廓，如圖8（c）所示。

設所有輪廓線段的頂點集合為P，任意一條輪廓線段Eɑb對應的兩個頂點為()Vɑ，Vb，O為每一條獨立輪廓的點的有序集合（列表）。算法為cɑlc_outline，形參*P、*V、*O是指針傳遞形式。截面輪廓線段判斷連接的算法偽代碼，如圖9所示。

圖9 算法偽代碼Fig.9 Algorithm Pseudocode

4 實例測試與數據驗證

4.1 測試環境

基于所提出的STL文件截面輪廓線段連接算法，借助開源的三維模型顯示平臺，在計算機中編程開發了面向STL文件的截面輪廓生成模塊。具體的測試環境參數如下：

4.2 數據驗證

將多個STL文件輸入至測試平臺，并通過截面輪廓生成模塊的數據處理，驗證所提出截面輪廓線段連接算法的有效性。軟件運行及數據處理的最終效果，如圖10所示。可見所提算法可通過STL文件的直接數據處理，避免模型數據的拓撲數據操作，快速有效的生成3D打印中模型數據的截面輪廓。

圖10 算法測試及效果顯示Fig.10 Algorithm Test and Effect Display

5 結論

面向3D打印中模型數據的截面輪廓求取問題，重點研究了STL文件的截面求交操作與輪廓線段的連接方法，通過STL文件的計算機數據格式特征分析，提出了面向STL文件的截面輪廓線段連接算法。首先，通過STL文件的相交面片選取與求交坐標計算，直接生成了相交截面的輪廓線段；然后，通過輪廓線段的連接判斷，快速生成了模型數據的截面輪廓；最后，借助PythonOCC的開源三維模型顯示平臺，使用Python的計算機編程語言編程開發了面向STL文件的截面輪廓生成模塊，并通過多個模型的數據測試對所提算法的有效性給予了驗證。實驗結果表明，所提出算法可通過STL 文件的直接數據處理，避免模型數據的拓撲數據操作，快速有效的生成3D打印中模型數據的截面輪廓。