內燃搗固鎬沖擊特性仿真研究與分析

王 滔，劉 歡，王 黎，王 杰

（四川大學機械工程學院，四川 成都 610065）

1 引言

搗固鎬是一種廣泛應用于鐵路施工、維修作業中的小型養護機械，主要應用于鐵路道碴的搗固作業[1]。沖擊系統是搗固鎬的核心部分，它是一種以高壓氣體為動力，驅動沖擊內筒往復運動，將氣體壓力能轉化為機械能，使得軌枕底部道碴重新排列的專用機械裝置[2]。目前，國內市場由Atlas Copco、Wacker Neuson等國外品牌主導。國內對搗固鎬的研究只是一種局部化的工作，主要是在國外已有的技術基礎上，對局部零件進行優化研究，但國產搗固鎬在技術設計水平上整體還存在較大差距。文獻[3]對搗固鎬激振力的評測方法進行了系統的研究；文獻[4]使用有限元分析軟件ANSYS，針對ZCD-300型搗固鎬進行了振動特性分析，得到了該型搗固鎬工作狀態下手持裝置的固有頻率和振型；文獻[5]研究了材料在沖擊載荷下的動態斷裂問題；文獻[6]針對沖擊機具作業時的能量傳遞進行了研究，闡明了沖擊能量的轉化過程。

作業時，搗固鎬的沖擊內筒直徑及質量對沖擊系統運動特性及輸出沖擊能影響極大。而對于搗固鎬沖擊系統中沖擊內筒的交變運動特性分析及結構參數影響，研究較少。鑒于此，以內燃沖擊搗固鎬為對象，提出基于AMESim仿真軟件的數值研究方法，進行數學建模并模擬分析，得到搗固鎬的運動特性為該類產品的設計及性能改進提供理論依據。

2 搗固鎬沖擊錘工作原理

內燃搗固鎬結構簡圖，如圖1所示。工作原理為：搗固鎬作業時，將鎬釬14插入軌枕下的石碴中，鎬釬與沖擊內筒8接觸。發動機1輸出的轉速和扭矩，通過摩擦離合器2傳遞給齒輪減速機構3，減速機構調整轉速和扭矩，并通過曲柄4帶動連桿5運動，將回轉運動轉換為壓氣活塞7在沖擊內筒中的往復運動。曲柄及連桿的原理為曲柄滑塊機構。沖擊內筒與壓氣活塞之間為密閉工作腔，工作腔中介質為空氣。工作腔在壓氣活塞的往復運動作用下產生周期性變化的壓強，不斷吸附和驅動沖擊內筒在外筒6中做直線往復運動，鎬釬受到沖擊內筒的周期性沖擊，最終完成沖擊能的輸出。

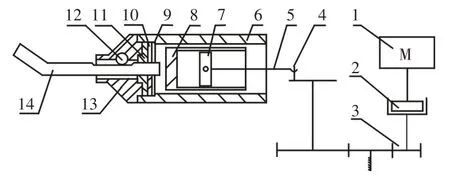
圖1 內燃搗固鎬主要結構簡圖Fig.1 Main Structure of Tamping Pick

3 沖擊系統數學模型

3.1 模型假設條件

為研究搗固鎬的沖擊系統運動特性與系統結構參數間的關系，有必要建立沖擊系統數學模型。由于系統實際情況比較復雜，且在建模中有些因素并不是主要的，可以忽略。因此，根據內燃搗固鎬的實際工作情況，作出如下假設：

（1）曲柄工作穩定時做勻速旋轉運動；

（2）沖擊內筒撞擊鎬釬的位置不變；

（3）在很短時間的一個周期內，忽略壓氣活塞與沖擊內筒間的氣體泄漏。

（4）由于氣體分子熱運動的速度比系統中各個氣體狀態的變化速率要快很多，所以將工作腔中的空氣視為理想氣體，即可以通過狀態方程描述氣體狀態之間的關系[7]；

（5）搗固鎬在高頻條件下工作，在短時間內可將工作腔中氣體的狀態變化視為絕熱過程[7]，忽略同外界環境中的能量交換。

3.2 建立數學模型

根據模型假設條件，對驅動機構以曲柄旋轉中心為原點，活塞直線運動方向為x軸，并定義壓縮工作腔為正方向建立坐標系，如圖2所示。

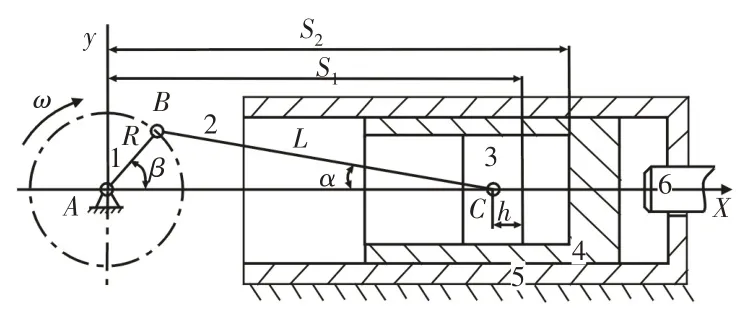
圖2 內燃搗固鎬沖擊系統簡圖Fig.2 Diagram of Tamping Pick Impact System

圖中：ω—曲柄角速度（rad/s）；R—曲柄長度（m）；L—連桿長度（m）；β—曲柄的角位移（rad）；α—連桿與x軸的夾角（rad）；S1—壓氣活塞的位移（m）；S2—沖擊內筒的位移（m）；h—壓氣活塞中心到活塞表面的距離（m）。3.2.1 工作腔氣體體積

式中：S—壓氣活塞和沖擊內筒的距離（m）；A—壓氣活塞端面面積（m2）；D1—壓氣活塞端面直徑（m）；v1—壓氣活塞速度（m/s）；v2—沖擊內筒速度（m/s）

3.2.2 工作腔氣體壓強

在搗固鎬的一個沖擊過程中，工作腔的壓強是實時變化的，其變化規律遵循氣體狀態方程，在絕熱條件下：

將式（7）帶入式（6）中，求導得工作腔空氣壓強隨時間的變化為：

式中：P—工作腔壓強（Pa）；V—某時刻工作腔體積（m3）；m—工作腔氣體質量（kg）；k—氣體絕熱指數，對于空氣取值1.4 ；Ve—氣體比容（m3/kg）。

3.2.3 工作腔氣體溫度

式中：T—工作腔氣體溫度（K）；P0—標準大氣壓，取值1.013×105Pa；T0—標準大氣溫度，取值273.15K。

3.2.4 工作腔氣體質量

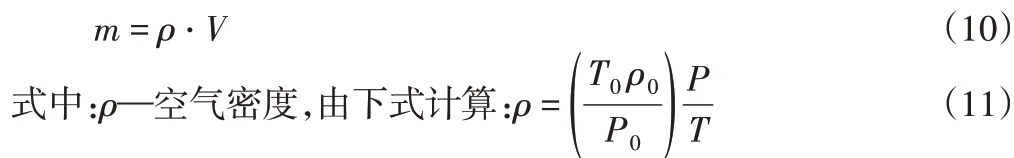
將式（4），式（9），式（11）帶入式（10）中：

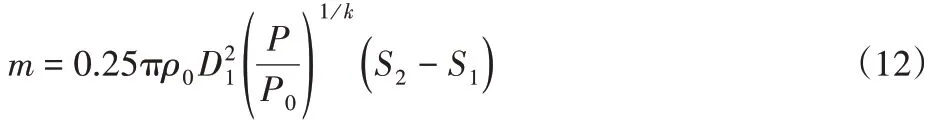
式中：ρ0—標準大氣密度，約為1.185kg/m3。

3.2.5 壓氣活塞的運動

曲柄在搗固鎬穩定工作階段做勻速旋轉運動，其轉速可由發動機轉速n計算。曲柄的角速度：

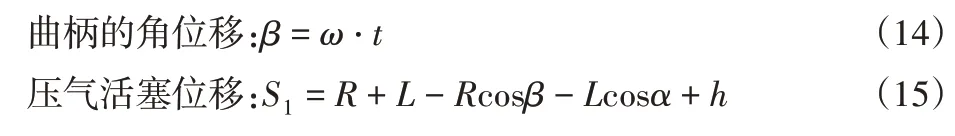
由式（13），式（14），式（15）得：

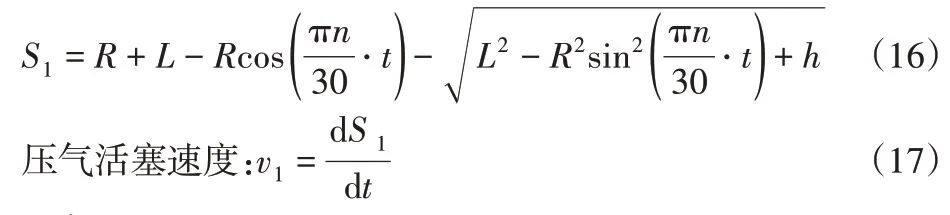
3.2.6 沖擊內筒的運動

沖擊內筒運動時主要受左右腔的壓差力、密封圈的摩擦力及其粘滯阻力，分析計算得：

式中：F2—沖擊內筒左右腔壓差力（N）；m2—沖擊內筒質量（kg）；ɑ2—沖擊內筒加速度（m/s2）；v2—沖擊內筒速度（m/s）；b—粘滯常數｛N/（m/s）｝，由于氣體粘滯阻力的阻尼常數很小，一般為10-3數量級，所以可以忽略站住阻力的影響，即bv2=0。可得沖擊內筒的運動加速度：

3.2.7 O型密封圈的摩擦力

壓力活塞在往復運動過程中，與沖擊內筒間存在摩擦力，主要為活塞上的O型密封圈與沖擊內筒內壁間的摩擦。這是一個動態、復雜的過程，所以摩擦力并不是一個常量，與密封圈材質、密封圈壓縮率、工作腔壓強等因素有關[8]。為使計算更加貼合工程實際情況，考慮密封氣腔壓力變化、O型圈壓縮率、沖擊活塞運動狀態變化等因素確定O型圈的總摩擦力計算公式[9]：

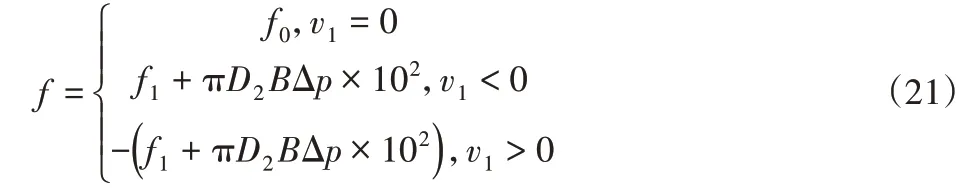
式中：f0—靜摩擦力（N）；f1—與O型密封圈壓縮率和潤滑工況有關的摩擦力（N），其模型，如圖3所示；D2—沖擊內筒直徑（m）；Δp—壓氣活塞兩側氣壓差（bar）；B—O 型密封圈被壓縮后與沖擊內筒壁接觸寬度（m），且B≈0.4w（w為O型密封圈截面直徑）。

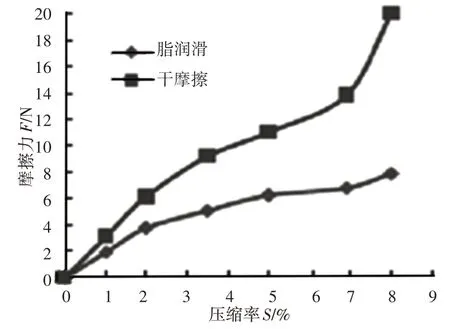
圖3 不同狀態下O型密封圈摩擦力Fig.3 Friction of O Ring under Different Condition

式中：dg—壓氣活塞凹槽直徑（m）；w—O型密封圈截面直徑（m）。

4 AMESim仿真分析

4.1 數值模型建立

搗固鎬試驗研究使用的動力源為一款歐瑪原裝進口汽油機，具體參數，如表1所示。

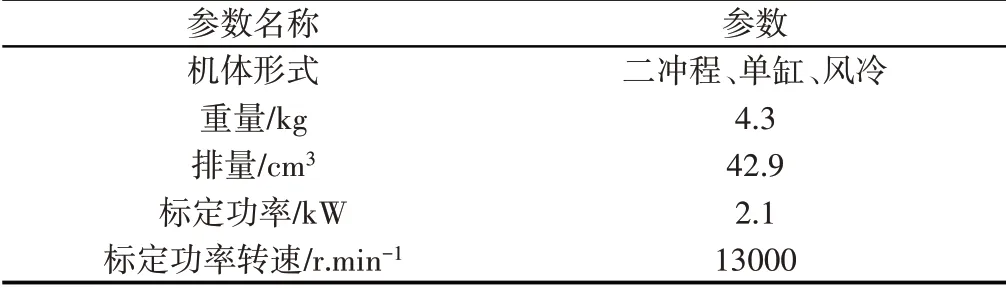
表1 汽油機主要技術參數Tab.1 Main Technical Parameters of Engine

汽油機標定功率為2.1kW，最高輸出轉速為13000r/min。搗固鎬齒輪減速機構的整體減速比i≈4.92，故能滿足的最大沖擊頻率約為43Hz，該頻率是仿真模型中設置電機模型參數的邊界條件。以搗固鎬沖擊系統的物理結構和數學模型為基礎[10]，搭建搗固鎬沖擊系統仿真模型，如圖4所示。

圖4 搗固鎬AMESim模型Fig.4 The AMESim Model of Tamping Pick

曲柄模型：將回轉運動轉換為直線往復運動，定義該模型的主要參數為曲柄長度、連桿長度以及補償量。

彈簧阻尼模型：位于曲柄連桿與壓氣活塞兩模型之間的彈簧阻尼模型，在仿真模型中只起紐帶作用，其功能是將左右端的兩個模塊連通起來。為了將左端的速度信號準確傳遞到右端，該模型的阻尼和剛度參數設置尤為重要。

活塞套筒模型：AMESim機械元件庫中提供了活塞與套筒模型，用于仿真帶有可運動外殼的物體的整體運動特性。定義該模型的參數主要有：活塞質量、內筒質量、內筒直徑、氣室初始厚度等。

O型密封圈模型：AMESim密封圈摩擦力模型提供了四種摩擦力計算方法，分別為用戶自定義參數模型、帕克摩擦力模型[11]、馬提尼摩擦力模型[12]、解析摩擦力模型[13]。參數設置時，考慮O型密封圈摩擦力模型的特點，選擇使用解析摩擦力模型。定義該模型的主要參數有O型密封圈材料楊氏模量、壓氣活塞凹槽直徑、沖擊內筒直徑、氣缸壁直徑、O型密封圈截面直徑等。

撞擊模型：在AMESim 軟件機械元件庫中有專門的撞擊模型，主要設置參數為撞擊起始間隔、接觸剛度、接觸阻尼等，其中影響質量體撞擊效果的主要為接觸剛度和接觸阻尼。

4.2 模型分析

（1）考慮了活塞與內筒間的摩擦力，基于摩擦力模型可以研究由于其他因素（如O型圈結構尺寸、有無潤滑等）而導致的不同動態摩擦力對沖擊內筒沖擊能的影響。

（2）撞擊模型的加入，可以研究不同反彈條件下沖擊內筒沖擊能的變化，即反映了不同的材質特性對沖擊能的影響。

（3）對搗固鎬沖擊能產生影響的結構參數，在模型中均可進行設置，如曲柄長度R、連桿長度L、沖擊內筒直徑D2、壓氣活塞直徑D1、工作腔初始長度S等在數學模型中出現的參數。仿真模型以內燃搗固鎬的實際測量值輸入參數[14]。關鍵參數列舉，如表2所示。

表2 仿真參數設置Tab.2 Simulation Parameter Setting

4.3 狀態量變化及分析

仿真步長取0.001s，各狀態量變化規律，如圖5～圖8 所示。根據仿真結果可知，沖擊內筒起始階段響應非常快，大約0.12s即可達到穩定運動階段。沖擊內筒的運動特性，如圖5～圖6所示。

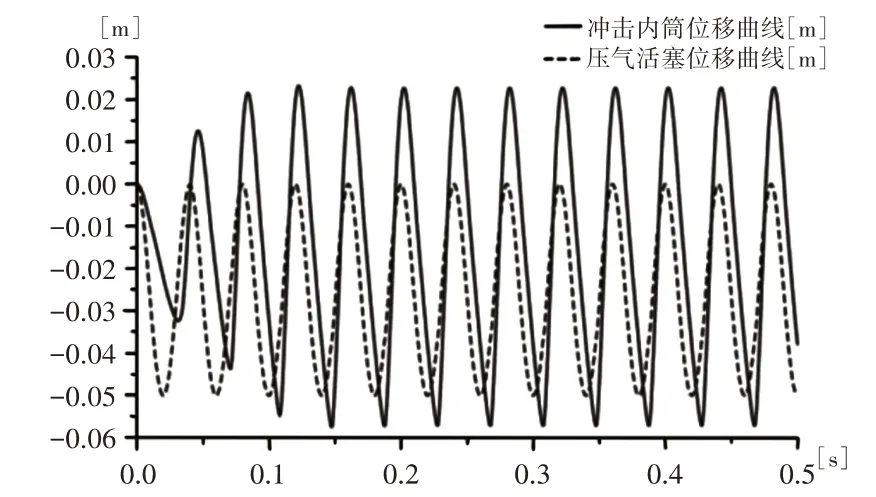
圖5 沖擊內筒與壓氣活塞位移曲線對比Fig.5 Displacement Contrast

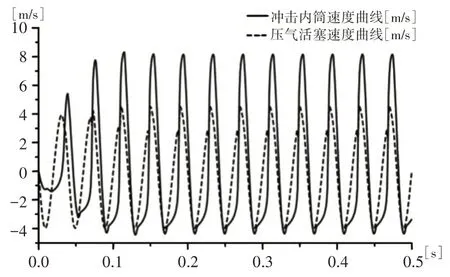
圖6 沖擊內筒與壓氣活塞速度曲線對比Fig.6 Speed Contrast

與壓氣活塞有一致的運動頻率，但在沖程和回程時間上不一致。壓氣活塞受曲柄勻速旋轉運動的影響，沖程和回程時間基本相等；而沖擊內筒受工作腔氣體變化及撞擊的影響，在一個周期內，沖程時間短，回程時間長。沖程運動主要發生在工作腔容積逐步減為最小時，壓氣活塞進入沖程開始壓縮空氣，工作腔中的溫度逐漸升高，開始儲存能量，當工作腔儲能達到最大后，驅動沖擊內筒加速撞擊鎬釬，同時釋放能量，完成內能到動能的轉化，溫度降到最低值，如圖7、圖8 所示。實際產品在額定沖擊頻率25Hz下的試驗沖擊能為55J。仿真模型在該額定頻率下沖擊內筒的沖擊速度為8.29m/s，沖擊能約為56.42J，與試驗沖擊能存在一定的差異，誤差為2.59%。原因為：（1）仿真模型中，沒有考慮運動過程中的氣體泄漏問題，因此導致理論沖擊效率偏高；（2）沖擊模型是為了模擬沖擊負載，由于實際產品的負載條件不清楚，不能完整還原搗固鎬的沖擊響應；（3）工作腔模型的深層結構仍是基于數學模型構建的，模型中氣體被假設為理想氣體，外部氣體的初始條件假設為標準大氣壓等，都會導致誤差出現。

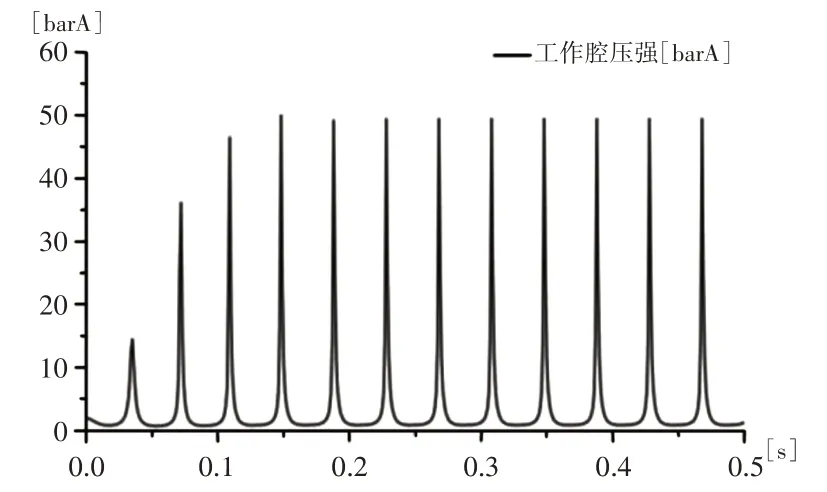
圖7 工作腔壓強曲線Fig.7 Pressure of Cylinder Working Chamber

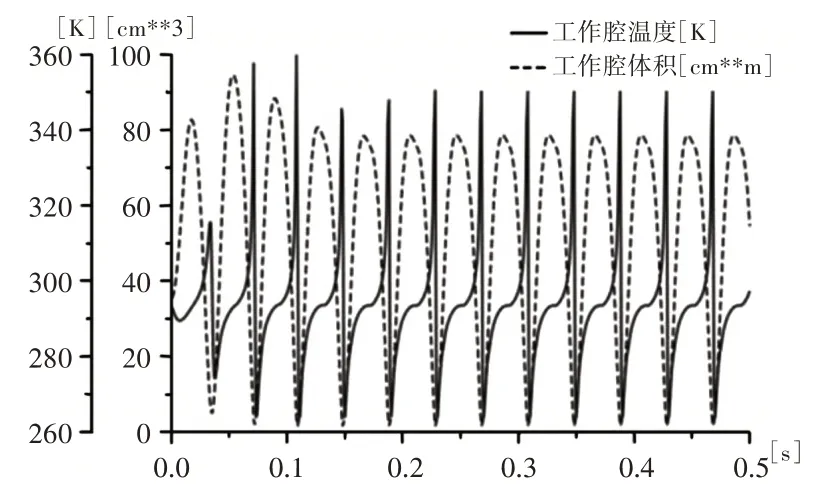
圖8 工作腔溫度、體積曲線Fig.8 Temperature and Volume of Cylinder Working Chamber

5 沖擊內筒對沖擊能的影響

5.1 沖擊內筒直徑對沖擊能的影響

沖擊內筒直徑的變化，將影響壓氣活塞的受力面積與工作腔氣體的體積。而壓氣活塞受力面積的變化影響對沖擊內筒的作用力，此外還將影響壓氣活塞與沖擊內筒間的配合狀態。為了保證單一參數變化帶來的影響，則相應的結構尺寸需要配合調整，如活塞凹槽直徑。沖擊內筒直徑分別取35mm、45mm、55mm，沖擊頻率保持為25Hz，其他參數按照產品實際結構取值，得到不同直徑下的沖擊內筒速度，如圖9所示。

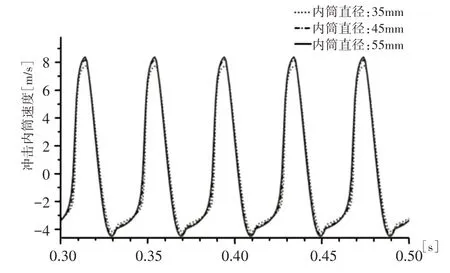
圖9 不同內筒直徑條件下，內筒速度變化Fig.9 The Change of Inner Cylinder Velocity with Different Inner Cylinder Diameter

由圖9 可知，當沖擊內筒直徑分別為35mm、45mm、55mm時，內筒的最大沖擊速度隨著內筒直徑的增大而增大，但增大幅度較小。理論沖擊能與沖擊內筒速度的平方成正比，故搗固鎬輸出沖擊能與內筒直徑應為正相關關系。為進一步研究內筒直徑與輸出沖擊能之間的細微關系，沖擊內筒直徑以2mm為差值在（35～65）mm之間取值，將得到的仿真結果代入MATLAB R2018b中求解，得到內筒直徑與輸出沖擊能的關系曲線，如圖10所示。

圖10 內筒直徑-沖擊能曲線Fig.10 Relationship between Impact Inner Cylinder Diameter and Impact Energy

由圖10可知，沖擊內筒直徑的變化對沖擊能的影響為非線性關系。原因為：沖擊內筒的直徑過小時，工作腔受力面積不足，導致回程階段沖擊能儲存不足；沖擊內筒的直徑過大，會造成因四周接觸摩擦阻力過大導致壓縮階段能量損失。當沖擊內筒直徑為（45～60）mm范圍時，沖擊能的損失較小；沖擊內筒直徑取為53mm時，沖擊能輸出效率最高。

5.2 沖擊內筒質量對沖擊能的影響

沖擊內筒質量與沖擊能理論上為線性關系，但是由于氣體流體及摩擦力的影響，沖擊內筒對沖擊能的影響便不再是簡單的線性關系。仍取該產品的沖擊頻率為25Hz，內筒質量分別取1.34kg、1.64kg、1.94kg，得到不同質量下的沖擊內筒速度，如圖11所示。

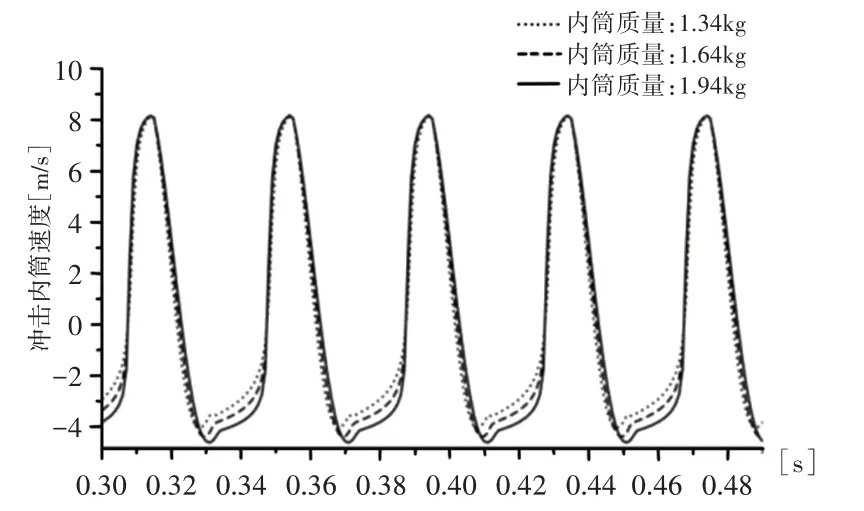
圖11 不同內筒直徑條件下，內筒速度變化Fig.11 The Change of Inner Cylinder Velocity with Different Inner Cylinder Mass

由圖11可知，當內筒質量分別取1.34kg、1.64kg、1.94kg時，內筒的最大沖擊速度無明顯變化。為進一步研究內筒質量與輸出沖擊能之間的相互關系，內筒質量以0.3kg為差值在（0.142～4.342）kg之間取值，同樣將仿真結果代入MATLAB R2018b中求解，得到內筒質量與輸出沖擊能的關系曲線，如圖12所示。由圖12可知：沖擊內筒的有效沖擊質量約為（0.3～3.6）kg之間，3.142kg為沖擊內筒質量的最佳取值，沖擊能可達到56.97J；仿真結果顯示：當內筒質量過大（大于3.742kg）時，沖擊能傳遞效率會極大降低。可能原因為：當內筒質量逐漸增大到一定的值時，沖擊內筒的加速度加速減小，在有限的時間內能達到的最終沖擊速度小，因此沖擊能輸出較低；而當內筒質量較小時，沖擊內筒加速度大，且能獲得較大的最終沖擊速度，但因零件質量較小，整體沖擊能輸出依然較低。因此，可以在（0.3～3.6）kg的范圍內通過改變沖擊內筒質量來改變沖擊能輸出，達到產品設計所需要的輸出值。

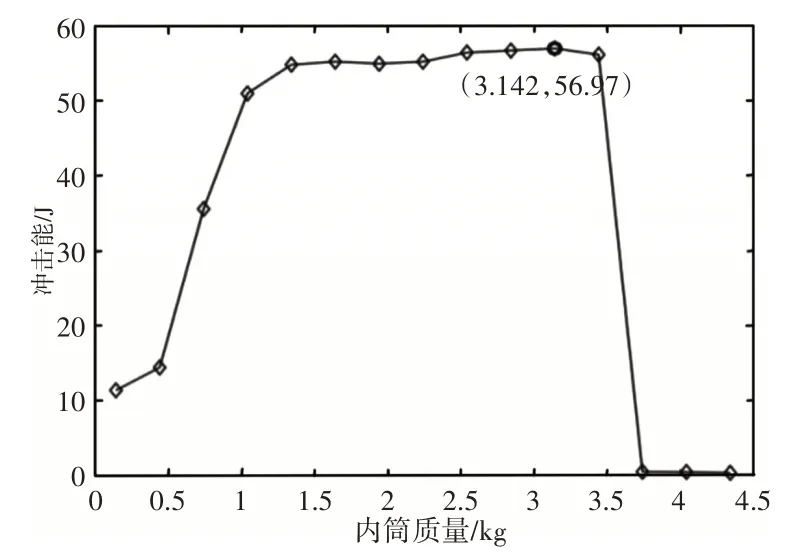
圖12 內筒質量-沖擊能曲線Fig.12 Relationship between Impact Inner Cylinder Quality and Impact Energy

6 結論

內燃搗固鎬作為一種高頻沖擊設備，通過分析其物理結構及工作原理，建立數學模型及仿真模型，驗證了該模型具有一定的正確性，可實現對內燃搗固鎬沖擊特性的快速研究，為新產品的研發提供理論支持，能夠彌補在實際開發過程中數據難采集、研究周期長等缺點。通過仿真模型分析，得出了搗固鎬沖擊系統各狀態量及輸出量的變化規律；詳細研究了沖擊內筒直徑、質量與沖擊能之間的影響關系，可為合理設計及優化該類型產品的氣動系統結構參數提供依據。