理工科專業基于MATLAB輔助線性代數教學改革與實踐

李泓霖

(重慶師范大學物理與電子工程學院 重慶 401331)

線性代數是各理工科專業的一門基礎必修課，具有廣泛的實用性，其主要研究線性空間相關問題，邏輯性較強。線性問題廣泛存在于各個科技領域，本課程所介紹的方法可適用于各個學科。通過該課程的學習，要求學生掌握線性代數的基本內容，如行列式、矩陣、線性方程組、線性空間等[1]；預期能夠使學生具備一定的空間想象力和分析解決問題的能力，為后繼專業課的學習做好必要的數學準備。這些學科特點對線性代數的教學提出了新要求，不僅要求學生掌握基礎的知識、具備解決基本問題的能力，還要在此基礎之上謀求創新發展。我國高校目前大多重知識輕實踐，對關鍵知識點的理解把握關注不夠。這就造成了許多應用型工科專業學生對相關概念的具體內涵不甚清楚。線性代數課程最大的特點是理論性強、知識體系涵蓋范圍廣，要求學生準確把握和理解關鍵知識點存在相當的難度。實際教學過程中發現，學生面對諸如轉置、分塊矩陣、向量內積，尤其是特征值和特征向量等抽象概念的時候，只能憑想象去理解而無法建立直觀的感受，因而常產生厭學情緒，傷害學生的積極性，教學效果往往不及預期[2]。針對上述線性代數課程特點，我們從教學模式方面進行了全新的嘗試。經過兩學期的教學實踐，發現利用MATLAB輔助教學可在最大程度上幫助學生直觀地理解線性代數的幾個重要概念并達到課程培養目的。

一、線性代數教學現狀

線性代數是我院電子專業本科學生的專業主干課程，其教學目標是使學生基本掌握幾類計算方法，較好地理解線性代數這門課的抽象理論，培養學生的創新能力、自學能力和應用能力。但以往課堂教學無法達到這種效果，主要是由于以下幾點問題：

（一）學習缺乏積極性

本專業的線性代數安排在大一上，與高數同步進行。此時學生不僅要適應高數的教學節奏，還要逐漸培養適合線性代數的學習策略。從實際反饋看，大一學生普遍反映線性代數難于高等數學，出現了畏學厭學、學習興趣減弱、積極性下降等情緒。這些現象主要是由于高數中如函數、導數等概念可以順利延續中學的理解，學生可以快速構建自己的數學體系來幫助理解新知識[3]。而線性代數的很多概念都是全新的，比如行列式、轉置、逆序數、矩陣、秩、正交等，而且線性代數知識體系有較強的內在關聯性和邏輯性，對大一新生而言，一旦初期跟不上，后續很難通過自學完成課程目標，導致失去學習興趣。

（二）知識體系聯系緊密、內容抽象

線性代數的知識點都具有一定的抽象性和概括性。教學中很多時候不可避免地脫離實際情景去講述重點難點，這樣教學模式就顯得單一，內容難免枯燥晦澀。此外，我們調研發現各大高校的線性代數教學安排普遍為32學時，考慮到實際情況我們學院增加到了48學時，但實際教學過程中仍感到學時略顯不足。

（三）教學模式傳統，學習方式單一

目前我院線性代數采用課堂講授、課后做題的傳統的授課模式，學生基數大，難于單個獨立輔導，學生在課堂上有疑問無法及時得到解決，只能對共性問題加以解釋[4]。為了在有限的時間內完成規定的課程目標和教學任務，教師往往專注于重要知識點的講授，側重于理論的闡述，而相應的背景知識、如何靈活運用、怎樣與專業知識相聯結等方面相應地有所減弱，這就會出現學生只懂得做題，而不會利用所學解決實際問題的情況。

（四）評價體系不完善

與大多數兄弟院校類似，目前我院對學生學習的考核方式為期中考試、平時成績和期末考試，各占30%、20%和50%。平時成績主要以考勤、作業及課堂表現進行考核。該考核體系測評因素多為考查學生的計算能力、知識點掌握的程度和一部分應用能力，而對學生的學習主動性、創新性、創造性等自主學習能力測查不夠。

二、針對線性代數教學現狀的改進措施

（一）著重培養學生的學習興趣和積極性

要提高學生對線性代數的學習興趣，需要加強所學知識與相關專業課程的融合，調整傳統單一授課模式，順應高校教學發展，將專業軟件、數學建模、數據分析等融入日常教學中，充分利用好工科專業具備的實訓環境與硬件資源，培養學生實際操作分析能力。以我院為例，近年來不斷加強線性代數與python、MATLAB、大數據分析等課程的整合溝通，讓學生切身感受到知識的應用價值。

（二）改進考核方式，增加實踐環節

課程考核是衡量教學成果、評價學習成效的重要環節。根據我們近幾年的實際教學經驗，可在原期中考試、平時成績和期末考試三部分中加入第四環節：課程實踐，占總成績的10%，期中考試分值降至20%。課程實踐采用課后作業形式自由發揮，遴選具有一定抽象性與發散性的知識點，結合實際背景，讓學生充分討論分析，查閱文獻等相關資料，最后以電子文檔形式給出解決方案。

（三）改進教學方法，豐富教學手段

加強線性代數知識的理解并為后續綜合應用需從兩方面認識：課堂知識與應用技能[5]。課堂知識是實踐應用的基礎，從程序本身講，線性代數中的絕大部分知識點都可用MATLAB來實踐。我們需要做的就是適當合理地引導學生，使其熟練掌握這些可由程序完成的運算操作。通過前期溝通，我們學院將MATLAB也安排在了大一上學期開設，這樣利用軟件來完成線性代數知識點的理解和鞏固成了最優的安排配置，以此提高學生運用知識的能力。讓學生運用MATLAB進行簡單操作，并實踐相關的知識點包括：行列式與矩陣、轉置的概念、矩陣的秩、矩陣的基本運算以及求解線性方程組等。

三、基于MATLAB平臺的實踐教學探索

要對線性代數進行教學改革，理論聯系實際則成了不可或缺的環節。最好的方式是讓學生自己動手，依托所學知識點進行相關具體探索與操作。矩陣及其運算、轉置、向量的內積等知識點往往抽象難懂，課堂講授的模式學生較難理解[6]。為了解決這一現實問題，我們結合同期開設的MATLAB課程搭建起了成本低、簡單易用、界面人性化的MATLAB實踐教學平臺，作為課堂講授的有效補充。

以第二章矩陣及其運算章節為例，矩陣的基本運算性質（假設運算可行）包括滿足交換律和結合律，而矩陣與數的乘法是將數乘矩陣A中的每一個元素。我們在解釋矩陣與數的乘法這一知識點時，讓學生做出一個矩陣圖形，然后對其進行數乘操作，可以非常直觀地理解為什么需要將數乘以矩陣A中的每一個元素。

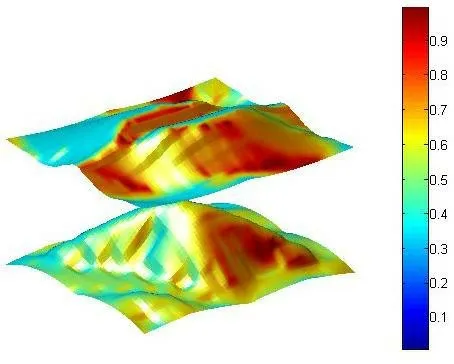
圖1 利用MATLAB對矩陣數據進行作圖（學生作業）

能帶結構是半導體物理中重要的基礎知識，我們給學生一個半導體能帶結構的矩陣數據，要求學生利用MATLAB作出相應圖形，而后進行數乘運算。能帶結構是半導體物理中的概念，貫穿電子專業后續必修課程的學習。對能帶的理解需要固體物理相關知識的支撐，這對學生存在一定的難度。這一步我們直接給出矩陣數據，讓學生自由作圖并修改。圖1為學生實際作出的能帶矩陣圖，從中可看出半導體的寬度及導帶和價帶等特征。如果對其進行數乘運算，則圖形整體將發生變化，這使得學生能夠直觀地看出為什么矩陣的數乘運算要對矩陣中的每一個元素進行操作，使學生明白其中的關聯。同時更可加深對晶體結構、作圖細節等技能的理解和掌握，為后續深入學習打好基礎。根據我們的觀察分析，這種實踐環節的加入能夠明顯提高學生的主動性和積極性。通過MATLAB輔助實踐教學，明顯改善了線性代數的教學效果，讓學生更深入地理解線性代數的基礎知識，激發了他們的創新思維和鉆研精神。

四、結束語

線性代數是工科專業的一門基礎必修課，不僅要求學生了解相關基本概念、基本知識和基本方法，為后續專業課打牢基礎，還要提高實際解決問題的能力。本專業的培育目標是為社會輸出合格的應用型人才，根據以往線性代數教學過程中存在的問題，我們對相關的教改內容提出幾點思考，并進行了有益探索。本文介紹了MATLAB在教學實踐方面的應用，結果顯示這種模式可初步解決線性代數課程抽象難懂的問題，激發學生的學習興趣，有效補充實踐教學環節。