稀疏對稱矩陣的LDLT分解在GPU上的高效實現

陳鑫峰，王武

1.中國科學院計算機網絡信息中心，北京 100190

2.中國科學院大學，北京 100049

引 言

稀疏對稱矩陣的LDLT分解對許多科學工程問題的有效求解非常重要。例如基于有限差分或有限元離散得到的稀疏線性系統，若采用迭代法難以奏效（迭代收斂很慢甚至不收斂）時，直接法LU分解便可有效解決問題。若矩陣具有對稱性，則LU分解轉化為LDLT分解。直接法分解過程計算開銷較大，如何提高其性能尤為重要。直接法的步驟可分為符號分解、數值分解和三角求解，其中數值分解最耗時。目前在多核或眾核上并行實現稀疏矩陣分解比較困難，因為分解過程中有較多的數據依賴和不規則數據訪問，導致難以充分利用這些多核CPU或加速卡，加速效果不佳，甚至無法加速。

基于CPU+GPU的并行異構架構已成為當今高性能計算機和服務器的主流體系結構之一。在GPU上稠密矩陣的計算已經具備很高的性能，如CUDA的cuBLAS庫[1]，因為稠密問題有利于高效內存訪問和存取，以及向量化計算指令集的應用。由于非零元素分布不規則的稀疏方程組難以高效訪存和向量化計算，無法充分利用GPU的計算資源實現高效求解。目前有很多適用于CPU的稀疏矩陣直接法求解器，比如SuperLU、MKL的PARDISO、MUMPS、UMFPACK、HSL[2]的MA57等，但是在GPU上有效實現稀疏矩陣分解的軟件還很少。CUDA的cuSOLVER[3]還沒有提供GPU上稀疏LU分解的接口。加州大學Peng等[4]開發了基于GPU的稀疏LU分解算法庫GLU 3.0，并用于集成電路仿真。它的數值分解較快，但符號分解存在瓶頸。如何有效利用GPU計算能力提升稀疏矩陣分解的性能仍是需要研究的課題[5]。

本文設計和實現了一種基于GPU的稀疏對稱矩陣的LDLT分解，該方法基于右視（right- looking）的LDLT分解，使得該分解可以實現右視算法的三層循環并行，這極大的提高了LDLT分解的并行度，并通過GPU動態并行技術提升了GPU的計算和訪存效率。本文最后針對一般稀疏對稱矩陣的一個典型測試集測試了該分解的性能。

實驗結果表明，本文提出的LDLT分解算法在NVIDIA TITAN V GPU測試平臺上達到較高的計算性能，針對稀疏對稱矩陣測試集，LDLT數值分解的計算速度相對于UMFPACK最高加速46.2倍，加速倍數取決于稀疏矩陣在分解過程中的非零元填充比。

本文結構如下：第1部分介紹LDLT的右視分解算法、符號分解和數值分解；第2部分重點介紹數值分解在GPU上的并行算法和實現；第3部分給出分解和求解算法在典型測試集上實現的性能，并與UMFPACK、MA57、cuSOLVER和GLU 3.0進行了性能對比。最后給出本文結論。

1 稀疏矩陣的LDLT 分解算法

1.1 LDLT分解的右視算法

階對稱矩陣A的LDLT分解可表示為A=LDLT，其中L是一個對角線元素為1的下三角矩陣，D是一個對角矩陣，而LT表示L的轉置。LDLT分解是高斯消去法的一個變型，即：

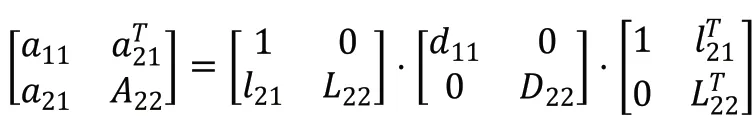
其中l11=1，d11和a11是標量，l21和a21是（n?1）×1的列向量，l22和D22以及A22是（n?1）階的子矩陣。由此可得到，d11=a11，l21=a21/d11，L22D22LT22=A22?l21d11lT22。一直重復該過程，直到求出L和D的所有元素，D的元素存儲在L的主對角線上。

右視算法每次迭代時先求解D的一個元素，然后求解一列L的元素，最后更新剩下的子矩陣。從中可以看到很大的數據依賴性，即必須先分解前k?1列，才能分解第k列，這極大的限制了并行性。

為了節省存儲空間，需要將稀疏矩陣壓縮后存儲，這導致稀疏矩陣非零元素的內存訪問極不規則。由于處理器對內存的訪問有空間局部性和時間局部性的特點，而LDLT分解過程中經常不規則跳躍式訪問數據，這與內存訪問特點相悖，因此極大地降低了性能，所以選擇一個適當的稀疏矩陣儲存格式很重要，本文采用壓縮稀疏列（Compressed Sparse Colum，CSC）格式，它一定程度上減少了不規則內存訪問。

稀疏矩陣A的CSC格式由三部分組成，分別為Ai，Ap和Ax，其中Ai表示稀疏矩陣A的行索引，大小為nnz（A的非零元素個數），Ap表示A的列指針，大小為n+1，n為A的維數，Ax表示A的非零元素值，大小為nnz。第k列元素的索引和值分別為Ai[Ap[k]],Ai[Ap[k]+1],…,Ai[Ap[k+1]-1]和Ax[Ap[k]],Ax[Ap[k]+1], …,Ax[Ap[k+1]- 1]。圖1是某個稀疏矩陣的非零元分布結構，●表示非零元素的位置。

圖1 稀疏矩陣分布Fig.1 The pattern of sparse matrix

算法1展示了右視LDLT分解算法的偽代碼，在這個偽代碼中，L表示初始矩陣A被符號分解后的矩陣，包括重排序和非零元填充（fill-in）。k表示當前列的索引，j表示當前列右邊的列。第k列被計算完成后，第j（j>k）列將會被立即更新。即第k列被計算完以后，該算法會向右看，使用算好的第k列更新第k列所有右邊的列j（j>k）。所以主要的操作變成子矩陣更新，該過程具有較好的并行性。

算法1.基于右視的LDLT分解

分解過程有3層循環，最外層的循環表示正在被分解的列，中間一層循環表示將要被更新的列，而最內層的循環表示待更新列的某個元素。顯而易見，最內層的兩個循環完全可以并行計算，后面介紹如何通過圖劃分實現最外層循環并行。

1.2 符號分解方法

由于本文待求解的稀疏矩陣是對稱的，并且符號分解不涉及任何具體的數值，所以本文使用稀疏Cholesky分解的符號分解[6-11]，這一部分時間很短，所以沒有使用GPU加速。這一步結束以后會將矩陣重新排列，即C=PTAP，其中P是排列矩陣，而且還會生成一個parent數組，表示列與列的依賴關系，即parent[i]=k表示第k列依賴第i列，也就表示必須先分解第i列，然后使用分解好的第i列更新第k列，最后才能分解第k列。這個parent數組也為后續的最外層循環并行提供基礎。

符號分解也需要為下一步的數值分解確定L矩陣的結構，因為對稱稀疏矩陣分解后，原先的零元素可能變成非零元素，即fill-in，所以需要盡可能的減少fill-in的數量。這就需要重排序算法，即減少fill-in的數量而提出的算法。符號分解主要包含以下4個步驟：

（1）重排序

該步驟通過對稀疏矩陣的非零元位置置換，即重排序來盡可能減少fill-in的數量。結束后會返回置換矩陣P，并使用該矩陣來重排序初始矩陣A，即C=PTAP。常用的重排序有近似最小度[12]（Approximate Minimum Degree, AMD）排序和METIS軟件包的圖劃分排序[13]，我們默認調用METIS重排序，對于規模較小的矩陣（比如n小于5000），則使用AMD重排序。METIS的排序算法基于多層次遞歸二分切分法、多層K路劃分法以及多約束劃分機制，執行效率更高，填充數量更少。

（2）尋找依賴圖

該步驟根據重排序后的矩陣C，尋找列與列之間的依賴關系，即依賴圖parent，數組parent[i]=k表示第k列依賴第i列，必須先分解完第i列，然后使用第i列更新第k列，最后才能分解第k列。可通過構造etree函數實現[14]。

圖2為圖1稀疏矩陣符號分解過程的依賴圖：其中節點表示列，邊表示列與列之間的依賴關系，且位于上面的節點所代表的列依賴下面節點所代表的列。從該依賴圖看出，分解完第1列后才能分解第6列；分解完第6列后才能分解第7列；分解完第7列后才能分解第9列；分解完第9列后才能分解第10列；分解完第10列后才能分解第11列。

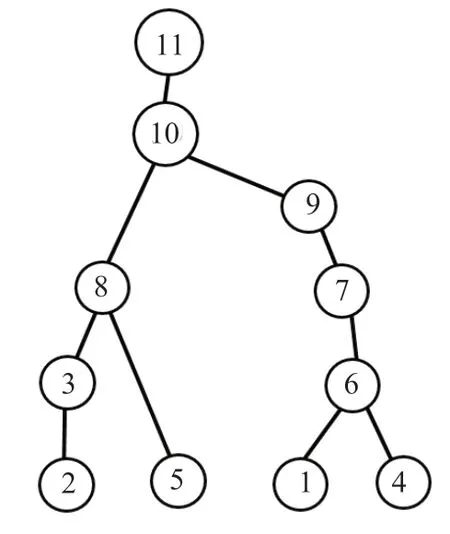
圖2 依賴圖Fig.2 The dependency graph

依賴圖為樹結構，對于一個樹節點，必須先分解完它的孩子節點所代表的列，然后使用它的孩子節點所代表的已分解好的列更新它自己所代表的列，最后才能分解它自己所代表的列。可見不同子樹代表的子列分解完全獨立，這進一步提升了并行度，即多層圖劃分并行。

（3）根據依賴圖確定levels

根據以上分析，我們可以實現層劃分并行。該步驟根據列與列的依賴關系，即依賴圖數組parent確定可并行計算的列，即level[]，同一個level中的列都可以并行分解，不同的level中的列有依賴關系，只能串行分解。

算法2為確定節點層劃分的算法偽代碼。其中葉子節點的層記作level 0，每個節點的層編號為它的左孩子節點的level值與右孩子節點的level值最大值取其較大者加1。level_i[]數組大小為n，它表示每一層包含的列編號，總層數為nlevel，數組level_p[]用于確定每層level_i的起始和終止列，大小為nlevel+1。例如第k層包含的列為level_i[level_p[k]],level_i[level_p[k]+1],…,level_i[level_p[k+1]-1]。這跟儲存稀疏矩陣的CSC格式類似，因此可通過level_i[]和level_p[]索引快速定位每層節點包含的列編號。

對圖2進行多層劃分后的依賴圖見圖3。其中屬于level 0的為第1、2、4、5列，這些列可以被并行分解。屬于level 1的為第3，6列，這些列必須等待level 0中的列被分解完以后才能被分解，同樣這些列也可以被并行分解。屬于level 2的為第7、8列，這些列必須等待level 1中的列被分解完以后才能被分解，同樣這些列可以被并行分解。屬于level 3的為第9列，這些列必須等待level 2中的列被分解完以后才能被分解，同樣這些列可以被并行分解。屬于level 4的為第10列，這些列必須等待level 3中的列被分解完以后才能被分解，同樣這些列可以被并行分解。屬于level 5的為第11列，這些列必須等level 4中的列被分解完以后才能被分解，同樣這些列可以被并行分解。

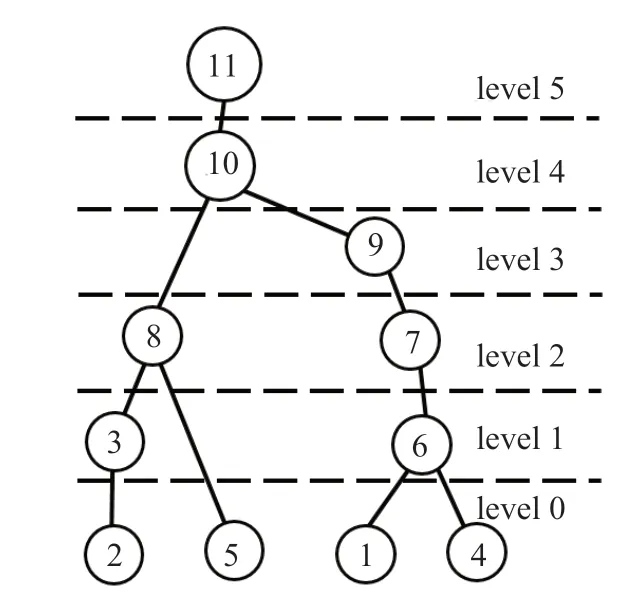
圖3 多層劃分后的依賴圖Fig.3 The dependency graph after level partition

（4）根據依賴圖數組確定L的結構

該步驟根據列與列之間的依賴關系，即依賴圖parent數組，來為下一步的數值分解確定L的結構。確定L結構的算法基于Cholesky分解的上視分解[6]，算法3為確定填充元位置的偽代碼，其中矩陣L第k行的非零元位置通過ereach函數[6]得到。圖4為圖1的稀疏矩陣符號分解填充后的L矩陣結構，其中●表示非零元素的位置，○表示填充元的位置。

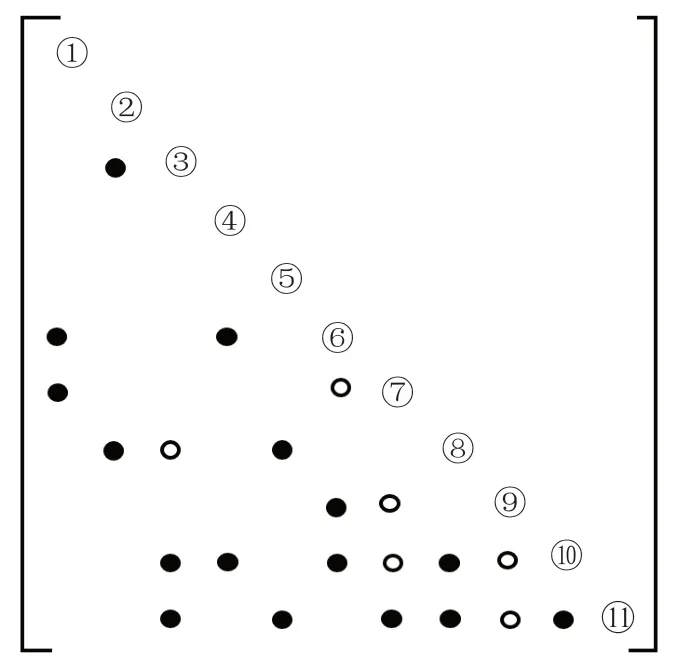
圖4 填充后的L矩陣Fig.4 The L matrix after fill-in

算法3.確定填充元的位置

17: Lx[p]= x[i];18: x[i]= 0; //為第k+1行清除x 19: end for 20: //存儲Lkk 21: p = c[k]++;22: Li[p]= k;23: Lx[p]= x[k];24: x[k]= 0;25: end for 26: Lp[n]= c[n-1];

1.3 并行數值分解方法

基于右視的LDLT分解算法見算法1，對應的并行數值分解過程的偽代碼見算法4[14]。

算法4.并行化的LDLT數值分解

其中第一層循環是選擇一個level的所有列，這些列可以被并行分解。

在第一層循環內部一共有兩個階段，第一階段為通過使用向量標量除法來并行分解當前選中的列，可以看出這些被選中的列可以被完全并行分解。第二階段為更新操作，即使用當前分解好的列來更新那些依賴該列的子列，這些子列很容易由以下方法定位：

假設當前被分解好的列為k，且lik≠ 0，lik≠ 0(i≥ j)，根據算法1中的第9行lij= lij- lik* ljk* lkk就可以知道lij≠ 0。所以如果lik≠ 0，則第i 列依賴第k列。為了快速判斷lik是否等于零，采用臨時非壓縮數組temp，即temp[i]=lik，如果temp[i]≠ 0，則表示lik≠ 0，這樣就可以快速定位和更新這些子列。從算法1的第9行也可以看到，該更新涉及到兩次乘法，為了提高數值分解速度，用了兩個臨時數組：tmpMem1[i]=lik*lkk，tmpMem[i]=lik。而且這些子列只是讀取這些臨時數組，并沒有更新它們，所以更新某個子列并不會影響其它子列的更新。

從算法1中可以看到，這些子列只更新一次且更新相互獨立，所以這些子列的更新完全可以被并行。第三層循環本質上是一個向量標量乘法和向量加法操作，即MAD操作，這個操作用來更新一個子列，算法1中子列每個元素的更新相互獨立，完全可以并行進行。可以看到，算法1的三層循環通過算法2和算法3實現完全并行，這有利于在GPU上提升性能。

1.4 三角求解方法

完成重排序、符號分解和LDLT數值分解之后，就可以求解線性方程組Ax = b，其中x可以是向量或矩陣，即同時求解多個有相同系數矩陣和不同右端向量b的線性方程組。因為C=PTAP，且C=LDLT，基于分解矩陣L、D和置換矩陣P，Ax = b的求解過程為：

(1)x=PTb;

(2)Ly=x;

(3)Dx=y;

(4)LTy=x;

(5)x=Py。

為了提高數值分解的并行度，沒有采用動態選主元，而是假設主對角元不為零，在分解過程中，如果主對角元足夠小，就將其賦值為常量，這會導致主對角元非常小的情況下數值分解后三角求解的計算結果有一定的誤差，為減少誤差，三角求解時使用迭代收斂[15-16]方法提高精度。相對于數值分解，三角求解的計算時間很短，沒有必要使用GPU加速。

2 LDLT數值分解在GPU上的實現

2.1 GPU架構和CUDA編程

GPU在科學與工程計算的很多應用領域發揮著越來越重要的作用[17-21]，尤其是對于計算密集型的應用。GPU由一組線程化的流多處理器（SM）構成，它們共享全局內存。每個SM含多個標量處理器、L1緩存、常量緩存（C-Cache）、多線程指令獲取(MT issue)以及共享內存等部件。線程是GPU的基本運算單元，多個線程構成線程塊，一個SM上可同時運行多個塊，塊內以單指令多線程（SIMT）方式執行程序。塊內的線程可實現同步。

CUDA作為GPU的編程模型，它支持核調用和核內存分配，從而充分利用GPU的并行計算能力。CUDA假設CPU和GPU有各自的內存空間，分別稱為主機內存和設備內存。同一個塊中所有線程可訪問同一共享內存，全局內存所有線程均可訪問。CUDA提供了blockIdx.x和threadIdx.x等內置變量，調用核函數時這些變量被自動確定，指引每個線程和塊的索引，將數據映射到對應的線程上，從而每個線程可獨立處理對應的數據。

2.2 LDLT數值分解在GPU上的實現

LDLT數值分解的算法偽代碼見偽代碼1，被重排序后的矩陣C=PTAP的列被劃分成了level層，即算法的最外層循環，每層的列可并行分解。前文已經表明，需要兩個臨時非壓縮的內存空間來更新子列，但是GPU的全局內存有限，所以需要提前判斷當前GPU還有多少全局內存可用。

在偽代碼1的第3行，free表示剩下可用的全局內存，單位是字節。因為level中的每一列分解都需要nB=2*n*sizeof(數據類型)字節的內存（算例中的矩陣數據是單精度的，可以是實數也可以是復數），而如果level中的列比free/nB還要大,尤其是n很大且level很小時，無法一次性全部并行分解完level中的所有列，必須分幾次才能完這些列的并行分解。

偽代碼1.基于GPU的并行LDLT數值分解

一旦確定了要并行分解的列，就要調用一個核函數（dynamic）來并行分解這些列，即偽代碼1的第14行，其中restCol表示當前需要并行分解的列數，該核函數調用表示每個線程塊負責分解一列，其偽代碼如下：

偽代碼2.動態并行分解核函數

10: update<<>>(Lp,Li,Lx,tmpMem,tmpMem1,n,k,blockIdx.x);11: cleartmpMem<<<(subColSize+1023)/1024,1024>>>(Lp,Li,tmpMem,tmpMem1,n,k,blockIdx.x);12: end function

在dynamic核函數中，每個線程首先確定當前被分解的列，然后再分別并行調用三個核函數factorize、update和clearTmpMem，它們分別表示分解當前列，用分解好的當前列更新依賴這一列的子列，以及清空分解當前列所使用的非壓縮的內存空間，它們的偽代碼分別為：

偽代碼3.當前列的多線程分解

偽代碼4.更新當前列的子列

14: atomicAdd(＆(Lx[Lp[j]+offset+threadIdx.x]), -x);15: end if 16: offset += blockDim.x;17: end while 18: end function

偽代碼5.清空當前列多線程分解所用內存

本文使用了CUDA C的動態并行（dynamic parallel）技術[20,22]。它支持嵌套執行內核函數，即從內核中啟動內核。動態并行的優勢是等內核執行的時候再配置創建網格和線程塊，這樣就可以動態的利用GPU硬件調度器和加載平衡器，通過動態調整適應負載。并且在內核中啟動內核可以減少一部分數據傳輸的開銷。動態并行技術尤其適合嵌套調用和遞歸調用的內核函數[22]，但只支持Nvidia推出的計算能力大于3.5的GPU設備。

3 數值結果

算法實現基于C/C++和CUDA C，編譯選項為-O3，其中GCC版本為4.8.5，CUDA的版本為11.1。測試平臺包含2個20核的Intel Xeon Gold 6148 CPU和4個NVIDIA TITAN V GPU，CPU主頻為2.4GHz，CPU端的內存為384GB，每張GPU卡的顯存為12GB。操作系統為Red Hat Linux 4.8.5-16。

實驗使用的測試集來自佛羅里達大學稀疏矩陣集[23]，它被廣泛用于稀疏矩陣基準測試，評價稀疏矩陣相關算法的性能。用于對比本文求解器性能的UMFPACK-5.6.2是稀疏數學庫SuiteSparse[24]的一個子集，它同時支持復數和實數矩陣的數值分解和直接法求解。

用于性能對比的稀疏矩陣直接法求解器還有HSL的MA57、CUDA自帶的cuSOLVER和加州大學Peng等開發的GLU。cuSPARSE只提供不完全LU分解，cuSOLVER的cusolverSp模塊雖然實現了稀疏矩陣的LU分解、Cholesky分解和QR分解，但目前的版本還沒有提供設備端的接口，因此無法通過GPU加速。GLU3.0在GPU上實現了稀疏矩陣的LU分解，并用于電路仿真，但只支持實數類型的稀疏矩陣。

利用CUDA實現的稀疏對稱矩陣的LDLT分解求解器在測試平臺上分解和求解各階段的運行時間見表1（其中數值分解在GPU上進行）；在CPU上采用UMFPACK、MA57和GPU上的LDLT數值分解的時間見圖5；采用UMFPACK、MA57、cuSOLVER和GPU上的LDLT求解器求解各階段的整體時間見圖6；本文求解器相比UMFPACK的LDLT數值分解的加速比和整個方程組求解時間的加速比見表2和圖7。圖表中的時間單位為毫秒（下同）。

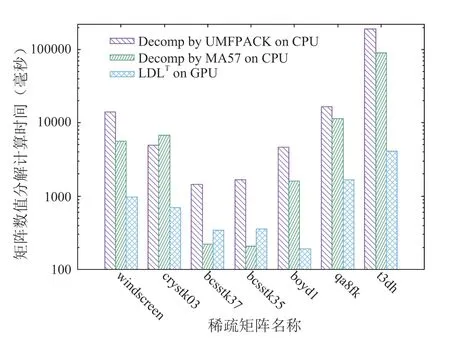
圖5 不同軟件數值分解的時間（毫秒）Fig.5 Runtime of LDLT (in ms)

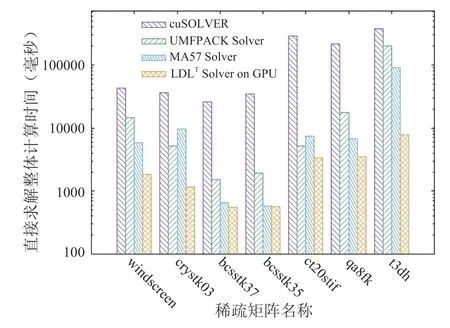
圖6 不同求解器的整體求解時間（毫秒）Fig.6 Total runtime of different solvers (in ms)

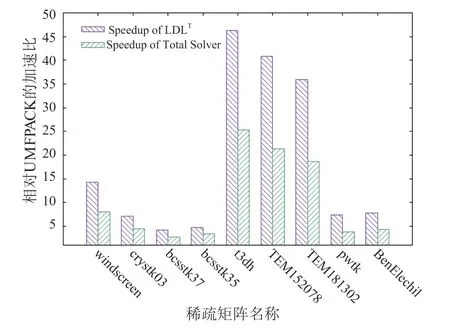
圖7 數值分解和整體求解的加速比Fig.7 Speedup of LDLT and total solver

表中的稀疏對稱矩陣以維數n排序的，考慮到并行度和內存限制，排除了1萬階以下和25萬階以上的矩陣集。其中matrix表示矩陣名稱，n表示矩陣的維數，nz表示初始矩陣的非零元個數（只包含了下三角部分），nnz表示本文求解器符號分解后的L矩陣的非零元個數。

nnz/nz表示fill-in的倍數。symbolic表示符號分解運行時間，numeric表示數值分解運行時間，solve表示三角求解運行時間，total表示本文求解器總的運行時間，為符號分解和數值分解以及三角求解運行時間之和，T(umf)表示UMFPACK總的運行時間，即符號分解和數值分解以及三角求解運行時間之和，Sp(ldlt)表示數值分解的加速比，Sp(total)表示總運行時間的加速比。

針對表1中列舉的矩陣，從表2可以看出，三角求解的運行時間遠少于數值分解的運行時間，因此表1中只對LDLT分解進行GPU加速。從表1和表2還可以看出，非零元填充比越高（即nnz/nz越大），LDLT數值分解的性能提升越明顯，因為更高的非零元填充比可以更好地利用右視分解算法的三層循環并行性，而且計算訪存比更高。

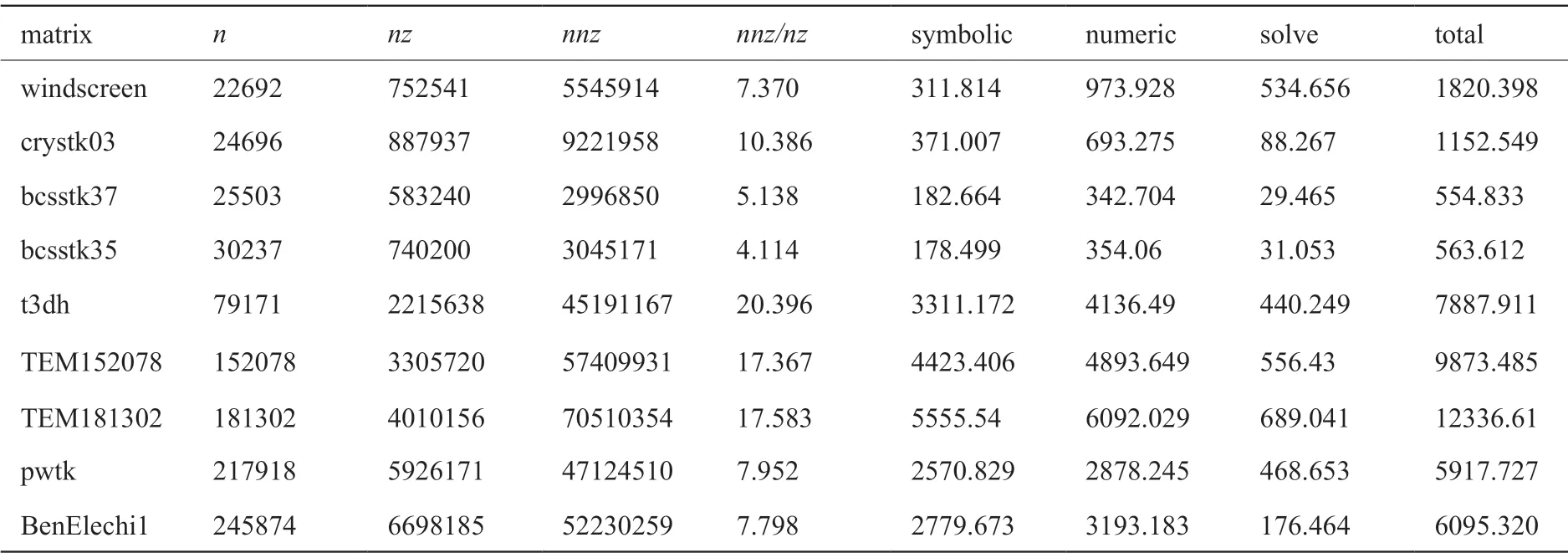
表1 基于本文的直接法求解、LDLT分解和求解階段的時間（ms）Table 1 Runtime (in ms)of LDLT decomposition and solving phases using our direct solver

從圖5、圖6可以看出，GPU上的LDLT求解器性能優于UMFPACK、MA57和cuSolver求解器，雖然對少數矩陣（如bcsstk37、bcsstk35），LDLT數值分解部分與MA57相比沒有加速，但求解總時間是最快的，因為其符號分解策略更佳。從圖7和表2可以看出，和UMFPACK相比，LDLT求解器數值分解階段最高可加速46.2倍，分解和求解總時間最高加速25.2倍。我們將LDLT與GLU 3.0的LU分解進行對比， GPU上的數值分解部分運行時間見圖8。從圖中可以看出，對于大多數算例，LDLT比GLU快2-8倍，僅對bcsstk37、bcsstk35兩個矩陣慢了10%。LDLT比GLU 3.0快的原因是采用了層次劃分和動態并行技術，且LDLT針對的是對稱矩陣，GLU3.0針對普通稀疏矩陣（對稱矩陣還要補齊另一半非零元數據）。但GLU在CPU端的符號分解部分的性能比2.2節的策略慢10倍以上，因此LDLT整體矩陣分解時間更快。

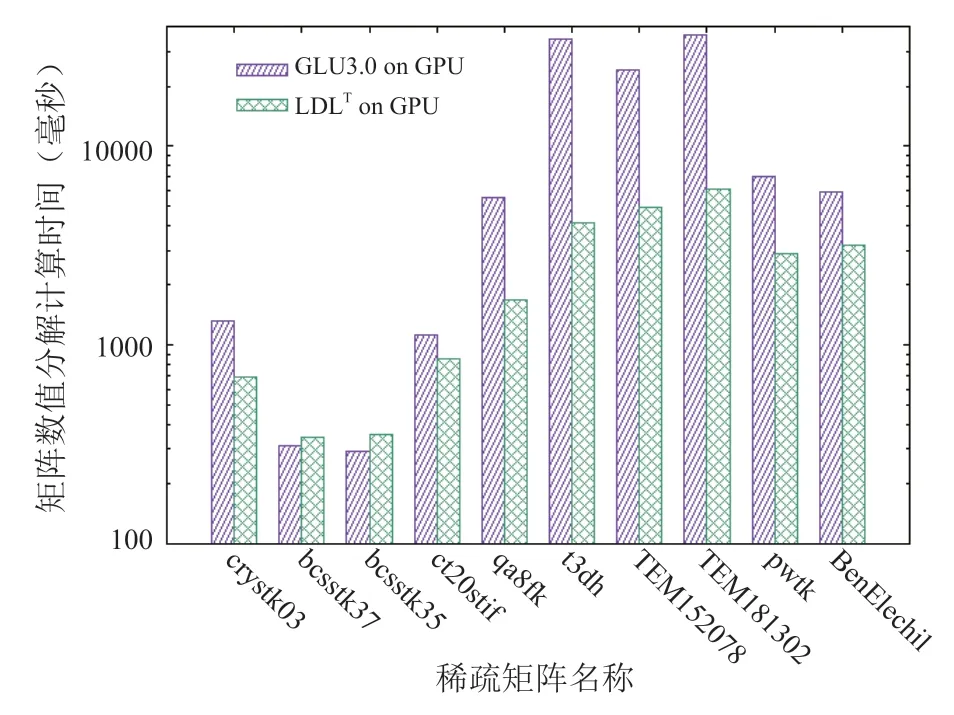
圖8 LDLT和GLU3.0在GPU上運行時間（毫秒）Fig.8 Runtime of LDLT and GLU 3.0 on GPU (in ms)

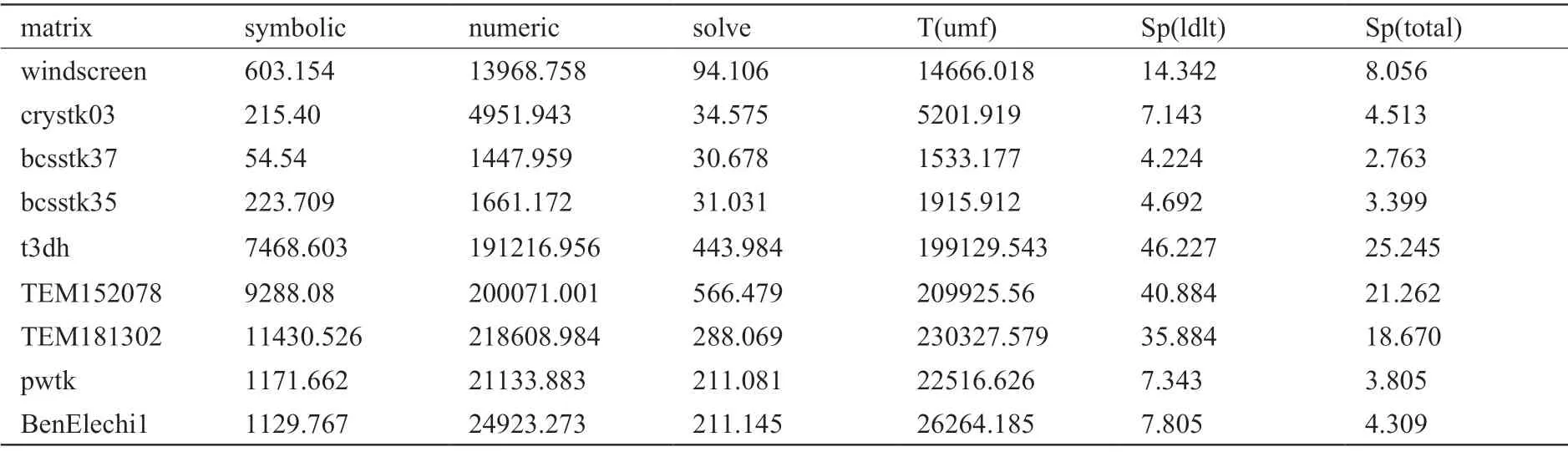
表2 UMFPACK的分解和求解各階段的時間（ms），以及本文求解器相對UMFPACK的加速比Table 2 Runtime (in ms)of LDLT decomposition and solving phases using UMFPACK solver, and the speedup of our solver compared with UMFPACK

4 結論與展望

本文設計并實現了一種基于GPU的稀疏對稱矩陣的LDLT求解器，該求解器采用Cholesky符號分解和右視算法的LDLT數值分解，并且該數值分解可以對右視分解算法的三層循環進行完全線程級并行計算，并采用依賴圖的層次劃分策略和CUDA的動態并行技術，這非常有利于LDLT數值分解在GPU上的加速。實驗結果表明，針對稀疏對稱矩陣測試集，GPU上實現的LDLT數值分解計算速度相對于CPU上的UMFPACK最高加速46.2倍，直接求解整體最高加速25.2倍。而且矩陣分解速度也快于加州大學Peng等開發的基于GPU的稀疏矩陣LU分解數值軟件包GLU3.0。

LDLT分解在GPU上的實現策略可為其它高性能GPU異構平臺上開展稀疏方程組的高性能數值求解器的設計實現提供借鑒，并有望應用于復雜電路仿真與設計、結構力學分析等領域的有限元離散線性方程組在GPU上快速高效求解。

利益沖突聲明

所有作者聲明不存在利益沖突關系。