利用等價無窮小替換求極限時應(yīng)注意的問題

黃 星，張倩瑤

(南陽職業(yè)學(xué)院，河南 南陽474500)

1 等價無窮小替換基本知識

知識1：無窮小的定義。如果當x→x0(或x→∞)時，函數(shù)f(x)的極限為零，則函數(shù)f(x)稱為當x→x0(或x→∞)時的無窮小量，簡稱為無窮小。

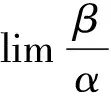
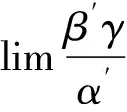
上述定理表明，當極限式為兩個無窮小之比或無窮小是極限式中的乘積因子且替換后極限存在，則可使用等價無窮小替換求極限。

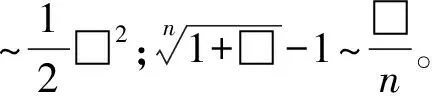
解法一(重要極限公式)：

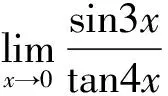
解法二(洛必達法則)：

解法三(等價無窮小替換)：

解法一(洛必達法則)：

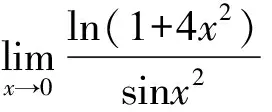
解法二(等價無窮小替換)：

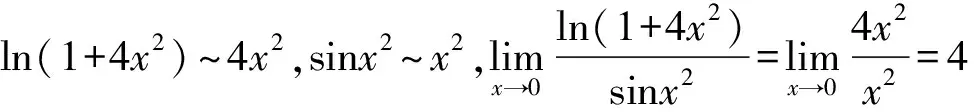
2 利用等價無窮小替換求極限應(yīng)注意的幾個問題

例3：指出下列解法的錯誤之處。

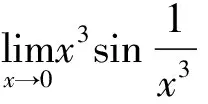
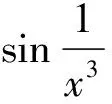
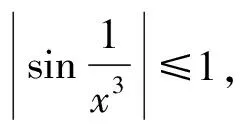
由例3可以看出，被替換的量在取極限時其極限必須為零，否則不能用等價無窮小替換。

例4：指出下列解法的錯誤之處。

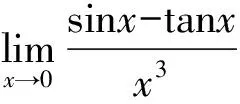
解： ∵x→0時，sinx～x，tanx～x，

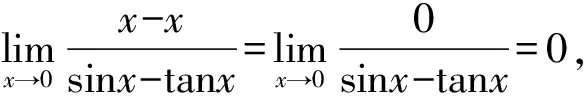
正確解法是：

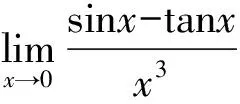
由例4可以看出，被替換的量作為乘除因子時可以用等價無窮小替換，而作為加減因子時就會出錯。事實上，等價無窮小替換在一定條件下對加減法也是成立的。等價無窮小替換對加減法成立的條件如下：

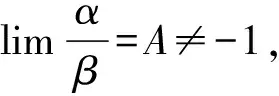
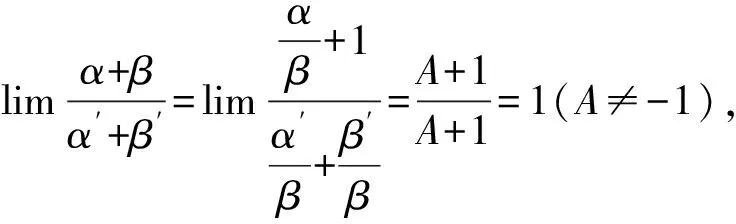
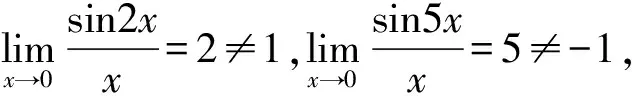
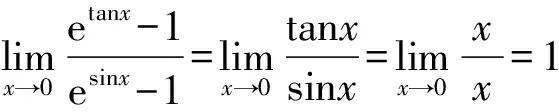
由等價無窮小替換對加減法成立的條件可知，不能直接用tanx-sinx去替換分子(etanx-1)-(esinx-1)，對于此題來說，等價無窮小替換對分子里的加減運算不適用，只能先將函數(shù)的分子恒等轉(zhuǎn)化為乘除運算，然后再用等價無窮小替換。

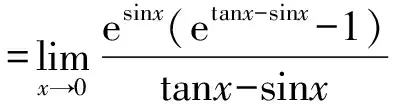
3 結(jié)語

在利用等價無窮小替換求極限時，要注意以下兩點：①被替換的量在取極限時其極限必須為零。②對于分子分母中的乘積因子，可以放心使用等價無窮小替換。若分子或分母是兩個等價無窮小之和或差，應(yīng)慎用此種方法。