一類各向異性非牛頓微極流體方程組弱解的存在性
王長佳, 石紹力
(長春理工大學 理學院, 長春 130022)
0 引 言
在三維空間中考慮如下一類各向異性非牛頓微極流體方程組的初邊值問題:

(1)
其中:Ω?3為一邊界充分光滑的有界區域,QT=Ω×[0,T],ΓT=?Ω×[0,T]; 未知向量函數u=(u1,u2,u3)表示流體速度,w=(w1,w2,w3)表示角速度,P表示壓力,f=(f1,f2,f3),g=(g1,g2,g3)為給定的外力項,Diu=(?iu1,?iu2,?iu3); 指數qi為給定的常數, 滿足1 微極流體方程是一類重要的偏微分方程, 在數學和物理中應用廣泛, 可描述一些經典Navier-Stokes方程無法處理的黏性不可壓縮流體的物理現象, 如動物血液的流動等. Araújo等[1]在具有Dirichlet邊界條件三維空間的有界光滑域中, 利用Faedo-Galerkin和緊致性論證的方法, 證明了非牛頓微極流體模型解的唯一性和周期性. 對于各向異性非牛頓流體, Antontsev等[2]研究了一類具有各向異性擴散的不可壓縮Navier-Stokes方程的演化問題, 證明了其第一初邊值問題弱解的存在性. 令q=(q1,q2,…,qN), 1 Lq(Ω)={u|u∈Lqi(Ω),i=1,2,…,N}, W1,q(Ω)={u|u∈W1,1(Ω),Diu∈Lqi(Ω),i=1,2,…,N}, 分別賦予范數 則其成為完備的線性賦范空間, 即Banach空間. 記β=max{q1,q2,…,qN},α=min{q1,q2,…,qN}, 為討論方便, 本文假設指數qi滿足α=q1≤q2≤…≤qN=β. 引理1[3]令Ω?N為一邊界充分光滑的有界開集.如果則如下嵌入關系成立: (2) (3) 注1由引理1, 本文假設指標qi(i=1,2,3)滿足條件1/q1+1/q2+1/q3>1. 下面考慮拋物型各項異性空間.令 (4) 2)u(0)=u0,w(0)=w0; 3) 對?φ∈Vq∩Lθ(Ω),φ∈L2(Ω)以及a.e.t∈[0,T], 有 注2在弱解定義1中未包含壓力項P.事實上, 若定義1中條件1),3)成立, 則由Rham定理知, 存在函數P∈L2(Ω)在廣義函數意義下滿足上述積分等式[4]. 注3定義1中,u(0)=u0,w(0)=w0在下列意義下成立: (5) (6) (7) 引理3[4]設X,Y為兩個Banach空間,X連續嵌入到Y.如果函數u∈L∞(0,T;X)且u: [0,T]→Y是弱連續的, 則u: [0,T]→X是弱連續的. 定理1設Ω?3為一個邊界充分光滑的有界開集,若則問題(1)至少存在一對弱解(u,w), 滿足 u∈CW([0,T];H)∩Lq(0,T;Vq),w∈CW([0,T];L2(Ω))∩L2(0,T;H01(Ω)), 其中: (8) u∈CW([0,T];X)表示u: [0,T]→X是弱連續的. 下面證明定理1. (9) 尋求問題(1)如下形式的近似解: 并且當m→∞時, um(0)=u0m→u0于H;wm(0)=w0m→w0于L2(Ω). (12) (15) 利用引理2、 H?lder不等式與Young不等式, 整理式(15)可得 將式(16),(17)相加, 并整理得 將式(18)在(0,t)(0≤t≤T)上積分, 可得 又對?φ∈Lqi(0,T;Vqi(Ω)), 有 利用估計式(20)可知 (22) 下面推導Ji(i=1,2,3,4,5)的估計. 對J2項, 利用引理2可得 對J3項有 對J4項, 利用式(15)有 (27) 對J5項有 (28) (29) 在廣義函數意義下, 將式(11)重寫為 (30) 下面逐項推導Ii的估計. 對I2項有 由式(20)知wm∈L2(0,T;W1,2(Ω))∩L∞(0,T;L2(Ω)), 故由文獻[8]中引理2.3.3知,wm∈L4(0,T;L3(Ω)), 從而 (32) 對I3項有 由式(15), 對I4項有 對I5項有 (35) 綜合式(32)~(35)并利用式(20)可得 (36) 由式(20),(22),(29),(36)可得下列收斂性: um→u強收斂于Lα(0,T;H), (38) 從而由式(20),(38)并利用插值定理可得 um→u強收斂于Lσ(0,T;H), ?σ≥1. (39) wm→w強收斂于L2(0,T;L2(Ω)). (40) 由上述收斂性, 在式(10),(11)中令m→∞取極限, 可得 當φ∈Vq,u∈L∞(0,T;H)∩Lq(0,T;Vq)時, 有 (43) 下面只需證明 (46) 由于對?ξ,η∈Lq(0,T;Vq),ξ≠η, 有 即Ai,A為單調算子, 因此可利用單調性方法證明式(46)成立. (47) 由α的定義及引理1知 于是由插值公式有 其次, 類似于文獻[6]中方法可知, 對a.e.t∈(0,T), 有 對?η∈Lq(0,T;Vq), 令 由A的單調性可知 (49) 由式(10)可知 令m→∞, 得 結合式(48),(49)可知 (50) 對任意的λ≥0,ξ∈Lq(0,T;Vq), 取η=u-λξ, 代入式(50)得 (51) 在式(51)中令λ→0取極限, 得 故S=A(u), a.e.(x,t)∈QT.定理1得證.1 預備知識










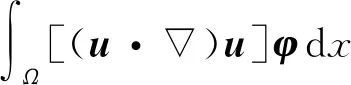



2 主要結果

2.1 近似解的構造




2.2 一致性先驗估計

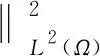














2.3 近似解的收斂性和存在性證明













