一個參數未知的網格多渦卷超混沌系統的自適應同步

許榮今, 李木子, 岳立娟

(東北師范大學 物理學院, 長春 130024)

由于網格多渦卷混沌系統具有更復雜的拓撲結構和動力學行為, 因此使網格混沌吸引子在信息加密和安全通信中具有廣泛的應用前景. Suykens等[1]在蔡氏系統上引入由絕對值函數組成的非線性函數, 構造了第一個單方向多渦卷混沌吸引子. 之后人們提出了應用分段線性函數、 階躍函數、 正弦函數、 雙曲正切函數等非線性函數構造單方向多渦卷混沌系統[2-7], 網格多渦卷混沌吸引子具有更高的復雜特性. 文獻[8-11]用不同的非線性函數構造網格多渦卷混沌系統: Yalcin等[8]提出了一個引入階躍函數構造的網格多渦卷混沌系統; Deng等[9]引入滯回函數構造了網格多渦卷混沌系統; 張朝霞等[10]在蔡氏系統上引入階躍函數和多項式構造了網格多渦卷混沌系統; Xu等[11]在三維系統中引入由雙曲正切函數組成的非線性函數構造了網格多渦卷混沌系統. 目前網格多渦卷系統大部分是混沌的, 但超混沌系統具有更復雜的動力學特性.

混沌同步方法包括廣義同步、 滑模同步、 反饋同步、 自適應同步等[12-16]. 其中自適應同步具有魯棒性強和穩定性高等特點. 在很多實際情況下, 系統參數不能確定, Park[17]提出了參數不確定R?ssler系統的自適應同步； 陳士華等[18]在參數辨識方法的基礎上, 研究了R?ssler超混沌系統自適應同步； 阿布都熱合曼·卡的爾等[19]研究了參數未知的統一超混沌系統自適應同步； 黃瑋[20]研究了參數未知Lü系統的自適應同步. 由于網格多渦卷混沌系統的構造更復雜, 因此對其同步的研究較少. 本文通過引入雙曲正切函數, 構成一個網格多渦卷超混沌系統, 相比于傳統的非線性函數, 雙曲正切函數作為連續可微函數, 更易分析混沌同步, 并有助于理解神經網絡存在的復雜動力學行為. 隨著渦卷數的增加, 系統的最大Lyapunov指數和復雜度均增加, 動力學特性變得更復雜. 本文基于Lyapunov指數穩定理論, 對該系統進行了參數未知的自適應同步研究. 數值仿真結果表明, 該方法可較好地實現參數不確定網格多渦卷超混沌系統的同步.

1 網格多渦卷超混沌系統模型及動力學分析

本文構造一個網格多渦卷混沌系統, 系統模型為

(1)

其中x,y,z,w,v為系統的狀態變量,a為系統參數,h(x)和f(y)為如下非線性函數：

通過改變h(x)和f(y)中的i和j擴展系統(1)的鞍焦平衡點個數, 進而產生任意連續的渦卷數.式(2)可在x方向產生偶數個渦卷, 式(3)可在x方向產生奇數個渦卷, 式(4)可在y方向產生偶數個渦卷, 式(5)可在y方向產生奇數個渦卷.鞍焦平衡點類型分為“指標1”和“指標2”兩種[21], “指標1”鞍焦平衡點用于產生鍵帶, “指標2”鞍焦平衡點用于產生渦卷.當參數a=1,h(x)選取式(2),f(y)選取式(4),i=1,j=1時, 有4×4個“指標2”鞍焦平衡點, 用“·”標出, 系統(1)在x-y平面的鞍焦平衡點分布如圖1所示, 由于每個“指標2”鞍焦平衡點對應1個渦卷, 因此網格渦卷的數量是4×4個.

圖1 4×4網格多渦卷吸引子的鞍焦平衡點分布Fig.1 Distribution of saddle focal equilibrium points of 4×4 grid multi-scroll attractors

系統(1)的吸引子相圖如圖2所示.當系統(1)的初值取(0.64,0.06,0,0.1,0),h(x)選取式(2),f(y)選取式(5),i=1,j=1時, 系統(1)產生的吸引子渦卷數為4×3, 如圖2(A)所示； 當h(x)選取式(2),f(y)選取式(4),i=1,j=1時, 系統(1)產生的吸引子渦卷數為4×4, 如圖2(B)所示； 當h(x)選取式(3),f(y)選取式(4),i=1,j=1時, 系統(1)產生的吸引子渦卷數為5×4, 如圖2(C)所示； 當h(x)選取式(2),f(y)選取式(4),i=2,j=2時, 系統(1)產生的吸引子渦卷數為6×6, 如圖2(D)所示.當渦卷數不同時, 對應Lyapunov指數列于表1.

圖2 系統(1)的吸引子相圖Fig.2 Attractor phase diagram of system (1)

表1 不同渦卷數的Lyapunov指數

由表1可見, 隨著渦卷數的增加, 系統(1)的Lyapunov指數始終有2個正的, 1個趨近于0, 2個負的, 在不同的渦卷數下, 始終均為超混沌狀態.

以4×6網格為例,h(x)選取式(2),f(y)選取(4)式,i=1,j=2, 當參數a改變時, 其狀態變量x和y的分岔圖如圖3所示, Lyapunov指數譜如圖4所示.

圖3 系統(1)隨a變化的分岔圖Fig.3 Bifurcation diagram of system (1) with a variation

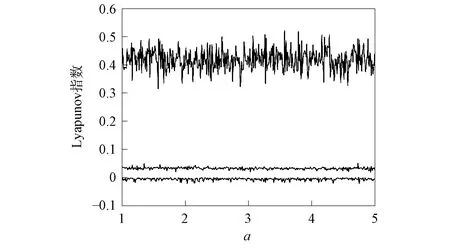
圖4 系統(1)隨a變化的Lyapunov指數譜Fig.4 Lyapunov exponential spectrum of system (1) with a variation

由圖3可見, 在x方向有并行的4條線, 在y方向有并行的6條線, 即系統(1)此時渦卷數為4×6.由圖4可見, 當a從1變化到5時, 始終有2個正Lyapunov指數、 1個趨近于0、 2個負的Lyapunov指數(未畫出), 系統處于超混沌狀態.

為進一步探討網格多渦卷超混沌系統的復雜性, 用文獻[22]中計算復雜度的方法研究系統(1)的復雜度, 計算網格混沌吸引子在x和y方向的復雜度, 結果列于表2.由表2可見, 隨著網格渦卷數的增加, 系統在x和y方向的復雜度明顯增加, 系統的復雜度越大, 其保密通信的效果越好.

表2 網格多渦卷混沌系統的復雜度

2 參數未知網格多渦卷超混沌系統的自適應同步

系統(1)為驅動系統, 響應系統為

(6)

其中a1為響應系統中需估計的參數,u=(u1,u2,u3,u4,u5)T為控制器.

定義誤差為

(7)

則誤差系統為

(8)

設計控制器為

(9)

參數自適應律為

(10)

選取Lyapunov函數為

(11)

對V求導可得

選取驅動系統(1)的初值為(5,-3,5,-3,0), 響應系統(6)的初值為(-1,-1,-1,5,2), 取α1=10.9,α2=10.95,α3=10.85,α4=10.8,α5=10.8,η=0.95,ei(i=1,2,3,4,5)隨時間t的變化如圖5所示.由圖5可見, 誤差快速趨近于0.參數自適應律ki(i=1,2,3,4,5)收斂曲線如圖6所示.由圖6可見, 參數ki在較短的時間內趨近于常數.參數a的辨識曲線如圖7所示.由圖7可見, 參數a在較短的時間內穩定收斂于估計值.

圖5 ei(i=1,2,3,4,5)隨時間t的變化曲線Fig.5 Change curves of ei(i=1,2,3,4,5) with time t

圖6 參數自適應律ki(i=1,2,3,4,5)的控制曲線Fig.6 Control curves of parameter adaptive law ki(i=1,2,3,4,5)

圖7 參數a的辨識曲線Fig.7 Identification curve of parameter a

綜上, 本文提出了一個網格多渦卷超混沌系統, 該系統僅有一個參數, 通過對系統Lyapunov指數譜的分析表明, 當參數變化范圍較大時, 該系統始終處于超混沌狀態, 通過Lyapunov指數和復雜度的分析表明, 隨著渦卷數的增加, 系統的最大Lyapunov指數和復雜度均增加, 并根據Lyapunov穩定性理論對網格多渦卷超混沌系統進行了參數未知的自適應同步, 仿真結果表明, 該方法在較短的時間內實現了兩個系統同步, 且同步效果較好, 可應用于保密通信.