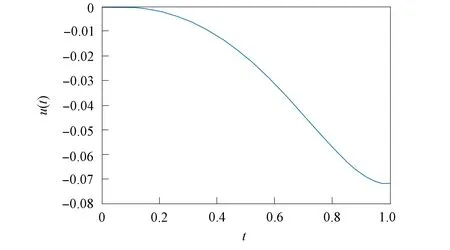
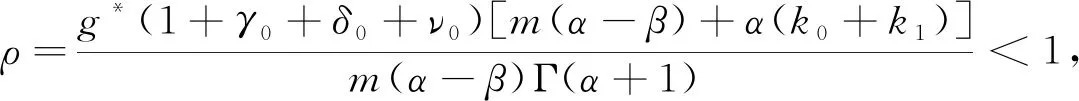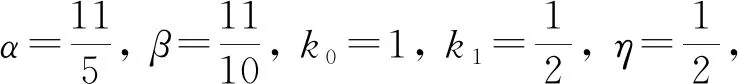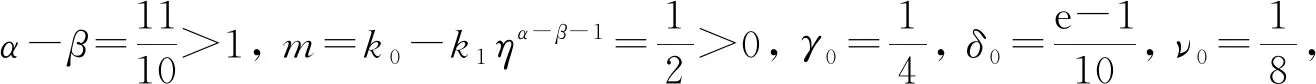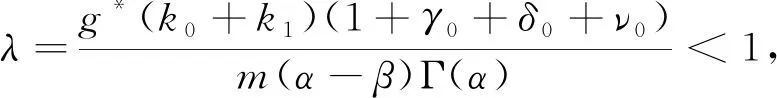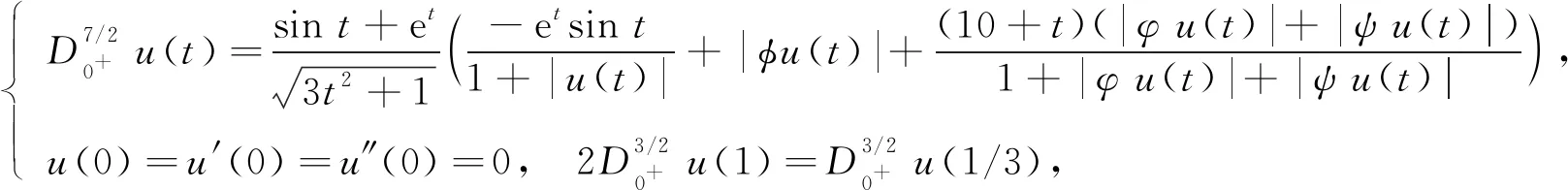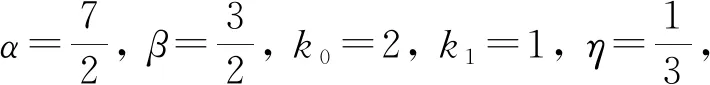一類非線性分數階積分微分方程解的存在性與模擬仿真
孫文超, 蘇有慧, 孫 愛
(1. 沈陽工業大學 理學院, 沈陽 110870; 2. 徐州工程學院 數學與統計學院, 江蘇 徐州 221018)
0 引 言
微分方程問題在物理、 化學、 生物和工程等領域應用廣泛[1-5], 目前, 關于分數階微分方程解的存在性研究已有很多結果[6-12]. 但實際問題中抽象出的方程通常可能是較復雜的且含有積分的分數階微分方程, 如擴散過程、 封閉系統中種群增長的Volterra模型及控制理論等[13-16]. 因此, 研究分數階積分微分方程尤為重要.
文獻[14]研究了如下分數階積分微分方程正解的存在性:
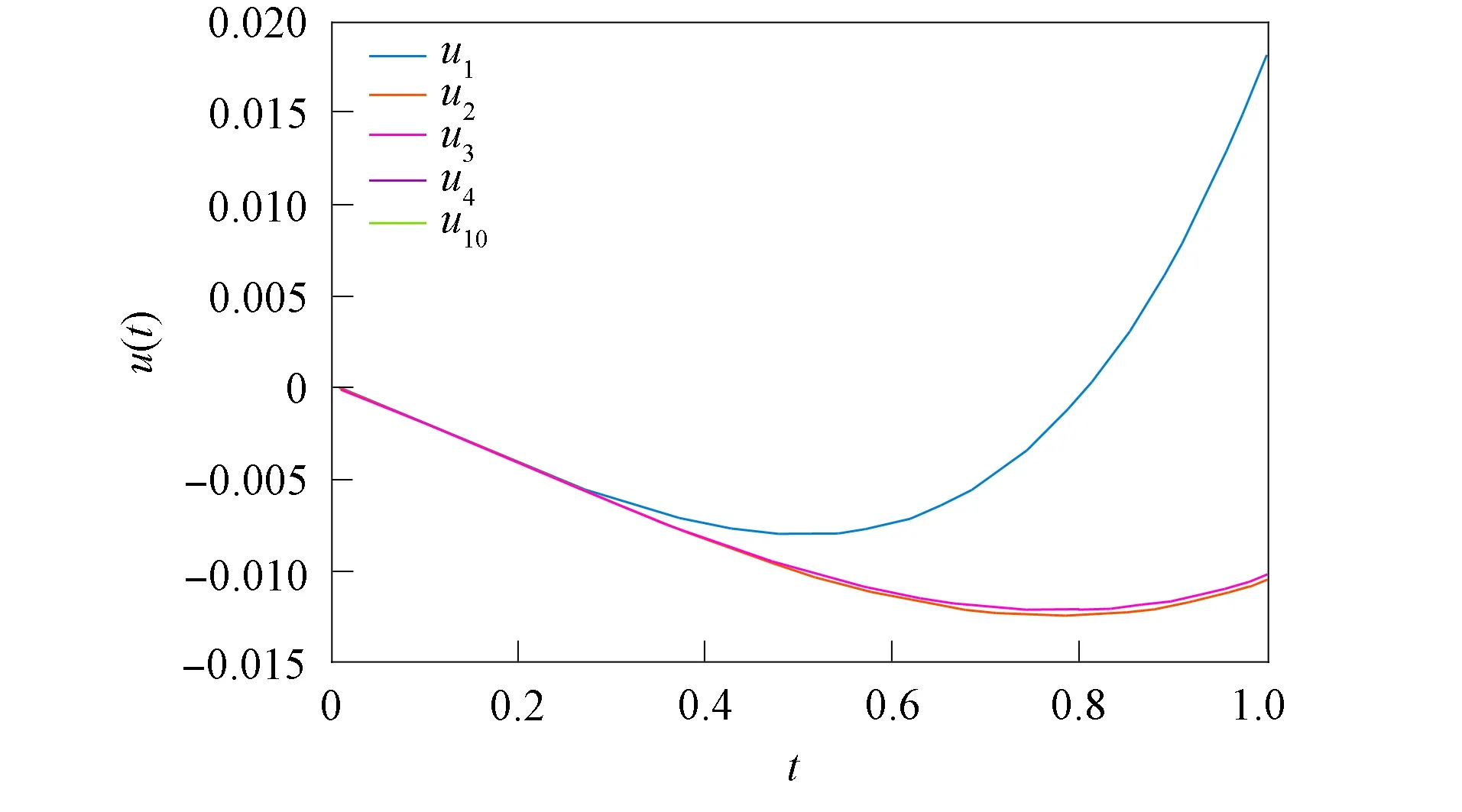
得到了其解的存在性和唯一性結果, 其中:n-1<α≤n, 0<μ 使用Krasnoselskii不動點定理, 得到了其至少存在一個解的結果, 其中: 1<α≤2, 0<β≤1;f: [0,1]×3→是連續的; 定義映射但上述結果都只從理論方面研究了分數階積分微分解的存在性, 關于其數值解方面的研究目前報道較少[17-18].基于此, 本文考慮如下非線性分數階積分微分方程: (1) 且滿足 通過使用Banach壓縮映射原理和Krasnoselskii不動點定理, 給出分數階積分微分方程(1)至少存在一個解和存在唯一解的結論.特別地, 通過模擬仿真實例說明本文主要結果的正確性. 定義1[19]令α>0, 函數u: (0,+∞)→的Riemann-Liouville分數階積分定義為 其中等式右端在(0,+∞)上有定義. 定義2[19]令α>0, 函數u: (0,+∞)→的Riemann-Liouville分數階導數定義為 其中n-1≤α 引理1[20]令α>0, 則有分數階微分方程 這里Ci∈,i=1,2,…,n,n=[α]+1. 引理2假設y∈C[0,1]且n-1<α (2) 有唯一解 (3) 這里m=k0-k1ηα-β-1>0. 證明: 根據引理1, 有 由u(0)=u′(0)=…=u(n-2)(0)=0, 可得 C2=C3=…=Cn-2=0, 因此 (4) 進一步可得 (5) 將式(5)代入式(4)即可推出式(3). 引理3(Krasnoselskii不動點定理)[21]設X是Banach空間E中的非空閉子集, 映射A,B滿足如下條件: 1) 當x,y∈X時,Ax+By∈X; 2)A是連續且緊的; 3)B是一個壓縮映射. 則存在z∈X, 使得z=Az+Bz. 假設: (H3) 存在一個常數b∈(0,α-n+1)和非負函數g(t)∈L1/b([0,1],(0,+∞)), 使得對任意的t∈[0,1],u,x,y,z,u′,x′,y′,z′∈, 均有 |f(t,u,x,y,z)-f(t,u′,x′,y′,z′)|≤g(t)(|u-u′|+|x-x′|+|y-y′|+|z-z′|). 定理1假設條件(H1)~(H3)成立, 且存在一個常數ρ, 如果 (6) 則邊值問題(1)有唯一解. 證明: 定義算子A:X→X為 令ΩR={u∈X: ‖u‖ 1) 對任意的u∈ΩR,Au∈ΩR. 對u∈?ΩR, 有 因此‖Au‖≤R, 從而A:ΩR→ΩR. 2)A是壓縮映射. 對任意的u,v∈ΩR,t∈[0,1], 有 因此, |Au(t)-Av(t)|≤ρ‖u-v‖, 故A在ΩR上是壓縮映射.根據Banach壓縮映射原理可知, 邊值問題(1)有唯一解. 例1考慮邊值問題: (9) 根據定理1可知, 分數階積分微分方程(9)有唯一解. 下面用迭代法對邊值問題(9)進行模擬仿真, 并給出其迭代過程曲線與逼近解.令 θ(t)=f(t,u(t),φu(t),φu(t),ψu(t)), (10) 其中 取初始值 迭代公式為 邊值問題(9)的迭代過程如圖1所示.由圖1可見, 其迭代過程是收斂的.圖2是邊值問題(9)經過10次迭代后的逼近解.由圖2可見, 分數階積分微分方程(9)有唯一解. 圖1 邊值問題(9)的迭代過程Fig.1 Iterative process of boundary value problem (9) 圖2 邊值問題(9)的逼近解Fig.2 Approximate solution of boundary value problem (9) 定理2假設條件(H1)~(H3)成立, 并且存在一個常數λ, 使得 (11) 則邊值問題(1)在X中至少存在一個解. 證明: 先將ΩR上的映射A分成A1和A2, 其中 下面分為三步證明. 1) 對任意的x,y∈ΩR, 有A1x+A2y∈ΩR. 根據式(7)中倒數第二個不等式, 可得 對任意的x,y∈ΩR,t∈[0,1], 有 因此,A1x+A2y∈ΩR. 2)A1是連續且緊的. 首先, 證明A1在ΩR上一致有界.顯然, 根據式(7)倒數第二個不等式的前兩項, 有 因此, 對任意的u∈ΩR,A1在ΩR上一致有界. 其次, 證明A1是等度連續的.由于f是連續的, 易知A1也是連續的.令u∈ΩR,t1,t2∈[0,1], 且 可得 因此, 如果t2→t1, 則有 |(A1u)(t2)-(A1u)(t1)|→0, 故A1是等度連續的.根據Arzela-Ascoli定理可知,A1在ΩR中是連續且緊的. 3)A2是一個壓縮映射. 對任意的u,v∈ΩR,t∈[0,1], 根據假設條件(H3), 有 由式(11)可知,A2是一個壓縮映射.因此, 引理3所有的條件都滿足, 故邊值問題(1)至少存在一個解. 例2考慮邊值問題: (12) 根據定理2可知, 分數階積分微分方程(12)至少存在一個解. 下面利用迭代法對邊值問題(12)進行模擬仿真, 并給出其迭代過程曲線與逼近解.令θ(t)定義如式(10), 其中 取初始值 迭代公式為 邊值問題(12)的迭代過程如圖3所示.由圖3可見, 其迭代過程收斂.圖4是邊值問題(12)經過15次迭代后的逼近解.由圖4可見, 分數階積分微分方程(12)至少存在一個解. 圖4 邊值問題(12)的逼近解Fig.4 Approximate solution of boundary value problem (12)
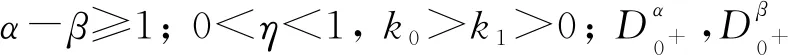
1 預備知識
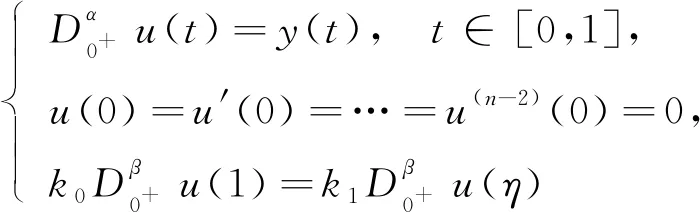

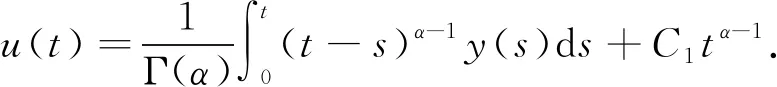
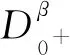

2 主要結果