Conformable分數階微分方程三點共振邊值問題解的存在性

江衛華, 董 倩

(河北科技大學 理學院, 石家莊 050018)

0 引 言

分數階微分和積分方程在流體力學、 化學工程、 機械學和控制論等領域應用廣泛, 最常見的分數階導數有Riemann-Liouville分數階和Caputo分數階導數等[1-6]. 目前, 關于一些常見的分數階微分方程邊值問題的研究已取得許多成果[7-9], 但對Conformable分數階導數的研究文獻報道較少[10-14]. Haddouchi[14]利用錐上不動點定理研究了如下Conformable分數階微分方程:

(1)

得到了該方程至少存在一個正解, 其中α∈(1,2],η∈(0,1] ,f: [0,1]×[0,∞)→[0,∞)是連續函數,Dα是Conformable分數階導數.

受上述研究啟發, 本文基于Conformable分數階導數, 討論下列三點共振邊值問題：

(2)

解的存在性, 其中1<α≤2,Dα是Conformable分數階微分.微分方程(2)滿足下列假設條件：

(H1)βη=1；

(H2) 映射f： [0,1]×2→滿足Caratheodory條件, 即當(x,y)∈2固定時, 對a.e.t∈[0,1],f(t,x,y)是t的可測函數； 當t固定時,f(t,x,y)是(x,y)的連續函數, 且對?r>0, 存在φr∈Y, 使得|f(t,x,y)|≤φr(t)成立, 其中|x|≤r, |y|≤r, a.e.t∈[0,1].

1 預備知識

設X,Y是實Banach空間,L: domL?X→Y是指數為0的Fredholm算子,P:X→X和Q:Y→Y是連續投影算子, 且滿足ImP=KerL, KerQ=ImL,X=KerL⊕KerP,Y=ImL⊕ImQ.因此L: domL∩KerP→ImL是可逆的, 用Kp表示其逆.

1) ?(u,λ)∈[(domLKerL)∩?Ω]×(0,1),Lu≠Nλu；

2) ?u∈KerL∩?Ω,Nu≠ImL；

3) deg(JQN|Ker L,Ω∩KerL,0)≠0, 這里J： ImQ→KerM是一個同構映射.

定義2[4]若α∈(n,n+1], 則函數y： [0,+∞)→的Conformable分數階積分為

(3)

其中式(3)右邊是在(0,+∞)上逐點定義的.

定義3[4]若α∈(0,1], 則連續函數y： [0,+∞)→的Conformable分數階導數為

(4)

若α∈(n,n+1], 則連續函數y： [0,+∞)→的Conformable分數階導數為

Dαy(t)=Dβy(n)(t),β=α-n.

(5)

其中式(4)和式(5)右邊是在(0,+∞)上逐點定義的.

引理1[10]若當t>0,α∈(n,n+1]時,y(n+1)(t)存在, 則有Dαy(t)=tn+1-αy(n+1)(t).

引理2[4]若當α∈(n,n+1]時,y(t)是在[0,∞)上的連續函數, 則對t>0, 有DαIαy(t)=y(t).

引理3[7]若當α∈(n,n+1]時,y(t)是α階可微的函數, 則對t∈(0,∞),Dαy(t)=0當且僅當y(t)=a0+a1t+…+antn, 其中ak∈,k=0,1,…,n.

引理4[7]當α∈(n,n+1]時, 如果Dαy(t)在[0,∞)上連續, 則

IαDαy(t)=a0+a1t+…+antn,ak∈,k=0,1,…,n.

2 主要結果

引理5(X,‖·‖),(Y,‖·‖)為Banach空間.

證明： 顯然, (X,‖·‖)是Banach空間.

假設{yn}是Y中的一個Cauchy數列, 則

(6)

顯然yn∈L[0,1], 又因為0<α<1,E=[0,1], 故對?δ>0, 有

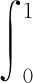
定義算子L： domL∩X→Y和算子N：X→Y分別為

Lu=Dαu(t),u∈domL,

Nu=f(t,u(t),u′(t)),u∈X,

其中

domL={u|u∈X,Dαu(t)∈Y,u(0)=0,u(1)=βu(η)}.

則微分方程邊值問題(2)等價于Lu=Nu,u∈domL.

引理6設條件(H1)成立, 則L: domL?X→Y是一個0指標的Fredholm算子.

證明： 顯然KerL={u∈domL|u(t)=ct, ?t∈[0,1],c∈}.

取y∈ImL, 則?u∈domL, 使得Lu=y, 即Dαu(t)=y(t).因此

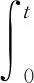
(7)

將邊值問題(2)的邊界條件代入式(7), 可得y滿足

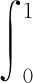
(8)

于是

另一方面, 若y∈Y滿足式(6), 則取

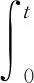
其中c是常數.易證u滿足邊值問題(2)的邊界條件, 于是

綜上可得

定義線性算子P:X→X為

Pu(t)=Dα-1u(1)t.

顯然P2u=Pu, ImP=KerL, KerP={u∈X|Dα-1u(0)=0},X=KerL⊕KerP.定義線性算子Q:Y→Y為

通過計算可得Q2y=Qy, 即Q是一個冪等算子, 是Y上的線性投影算子.顯然ImL=KerQ.任取y∈Y, 可寫成y=(y-Qy)+Qy, 其中(y-Qy)∈KerQ=ImL,Qy∈ImQ, 因此Y=ImL+ImQ.取y∈ImL∩ImQ, 由y∈ImQ得y=Qy, 由y∈ImL=KerQ得Qy=0, 因此y=0, 所以Y=ImL⊕ImQ.又因為dim KerL=1=co dim ImL, 所以L是一個0指標的Fredholm算子.證畢.

引理7定義線性算子Kp: ImL→Z為

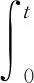
則Kp=(L|dom L∩Ker P)-1.

證明： 易證KP(ImL)?domL∩KerP.取y∈ImL, 可得Kpy∈domL∩KerP,LKpy=Dα(Iαy(t))=y(t).另一方面, 對u∈domL∩KerP, 由引理1可得

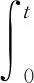
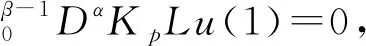
未缺血再灌注大鼠腦組織未出現腫脹，腦溝腦回清晰皮層顏色較紅潤；淺表血管豐富、充盈好、鮮紅，腦缺血再灌注大鼠腦組織有明顯腫脹腦溝腦回表淺，皮層顏色蒼白,表面血管塌陷，基本無血流[1]。如圖 1-2所示。

|f(t,u(t),u′(t))|≤φr(t),t∈[0,1].

本文假設如下條件成立：

(H3) 存在常數M, 使得對?t∈[0,1], 當u∈domL, |u′(t)|>M時, 有QNu≠0, 即

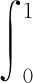
|f(t,x,y)|≤a(t)+b(t)|x|+c(t)|y|,t∈[0,1],x,y∈,

其中‖b‖Y+‖c‖Y<1/2;

(H5) 存在常數B>0, 使得當|c|>B時, 下列不等式之一成立：

1)cQN(ct)>0, ?t∈[0,1];

2)cQN(ct)<0, ?t∈[0,1].

引理9若條件(H3),(H4)成立, 則Ω1={u|u∈domL/KerL,Lu=λNu,λ∈[0,1]}在X中有界.

證明： 任取u∈Ω1, 則Lu=λNu,λ≠0,Nu∈ImL=KerQ.由條件(H3)知, 存在t0∈[0,1], 使得|u′(t0)|≤M, 由Lu=λNu和u(0)=0, 得

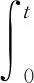
(9)

對式(9)兩邊求導, 得

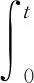
(10)

令t=t0, 代入式(10)得

從而

于是有

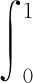
由|u′(t0)|≤M和條件(H4), 可得

因此可得

(11)

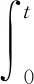
從而

再結合式(8)可知Ω1有界.證畢.

引理10若條件(H1)～(H3)成立, 則Ω2={u∈KerL|Nu∈ImL}在X中有界.

證明： 令u∈Ω2,u=ct,c∈,QNu=0, 則

由條件(H3)知, 存在t0∈[0,1], 使得|u′(t0)|≤M.又因為|u′(t)|=|c|≤M, 故Ω2有界.證畢.

引理11若條件(H1)～(H3),(H5)成立, 則集合

Ω3={u∈KerL|λJu+(1-λ)QNu=0,λ∈[0,1]}

在X中有界, 其中J: KerL→ImQ,J(ct)=c(c∈,t∈[0,1])是線性同構映射.

證明： 任取u∈Ω3, 則

u=ct,λJct+(1-λ)QN(ct)=0.

如果λ=1, 則c=0.如果λ=0, 則由條件(H5)可知|c|≤B.

對λ∈(0,1), 如果|c|>B, 則由條件(H5)可得

與已知條件矛盾.因此Ω3有界.

注1如果條件(H1),(H2),(H4)和(H5)中2)成立, 則集合

有界.

定理2假設條件(H1)～(H5)成立, 則邊值問題(1)至少有一個解.

1) ?(u,λ)∈[(domLKerL)∩?Ω]×(0,1),Lu≠Nλu；

2) ?u∈KerL∩?Ω,Nu≠ImL.

下面證明deg(JQN|Ker L,Ω∩KerL,0)≠0.令H(u,λ)=±λJu+(1-λ)QNu, 由引理11可知,H(u,λ)≠0,u∈?Ω∩KerL.由度的同倫不變性得

于是利用定理1可知, 微分方程邊值問題(2)在X上至少有一個解. 證畢.

綜上所述, 本文討論了Conformable分數階三點共振微分方程邊值問題, 通過定義合適的Banach空間、 范數及算子, 利用Mawhin重合度理論證明了其解的存在性.