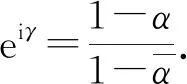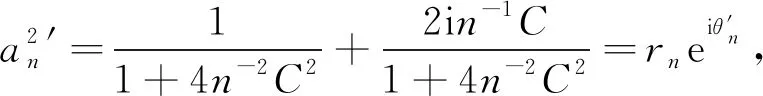圓盤自同構(gòu)迭代的零點序列與Blaschke乘積

和佳星, 曹 陽

(吉林大學 數(shù)學學院, 長春 130012)

1 引言與主要結(jié)果

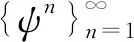
定義2[2]如果存在η∈(0,1), 使得水平集{z∈D; |u(z)|<η}是連通的, 則稱一個屬于H∞的內(nèi)函數(shù)為單分支[3]內(nèi)函數(shù).

Aleksandrov[4]給出了內(nèi)函數(shù)u(z)是單分支的充要條件為存在常數(shù)C=C(u), 使得對所有的a∈D, 均有

文獻[2]證明了幾類內(nèi)函數(shù)是否為單分支的, 如有限Blaschke乘積是單分支的, 但插值Blaschke乘積和無窮Blaschke乘積不一定是單分支的.

定義3[5]若存在正數(shù)δ>0, 使得B(z)滿足

則稱B(z)為插值Blaschke乘積.

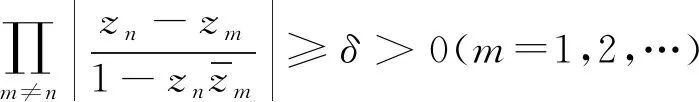
Dρ(an,r)={z∈D:ρ(z,an)<ε}

是兩兩分離的.

定義4[2]z與w在偽雙曲度量下的距離定義為

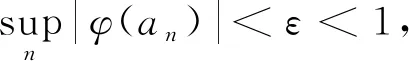
則存在一個常數(shù)γ, 使得

|B′(eiθ)|≤{γ|φ′(eiθ)| a.e.

如果f∈Aut(D)并且f不是恒同映射, 則f或者在圓盤D內(nèi)有一個不動點, 或者在圓周T上有兩個(可以重復)不動點.

定義5[6]圓盤中自同構(gòu)的分類定義如下：

1) 如果自同構(gòu)在圓盤D內(nèi)有且只有一個不動點, 則稱其為橢圓型的；

2) 如果自同構(gòu)在圓周T上有兩個不同的不動點, 則稱其為雙曲型的;

3) 如果自同構(gòu)在圓周T上有一個重復不動點, 則稱其為拋物型的.

定義6設(shè)f:D→D和g:D→D分別是拓撲空間D和D上的連續(xù)自映射, 如果存在同胚映射h:D→D, 使得h°f=g°h, 則稱f和g是拓撲共軛的.特別地, 如果f,g和h都是全純(線性, 光滑,cr可微)的, 則稱f和g是全純(線性, 光滑,cr可微)共軛的, 稱h是一個全純(線性, 光滑,cr可微)共軛.

因為上半平面與單位圓盤是全純共軛的, 因此本文利用文獻[7]中的分類進行討論, 將上半平面的全純自映射gi(z)通過全純共軛h(z)映射為單位圓盤上的全純自映射

并利用作用任意的單位圓盤自映射A(z)得到

定理1在單位圓盤的解析自同構(gòu)分類中, 拋物型的和雙曲型的在迭代后得到的零點均可構(gòu)成單分支的插值Blaschke乘積； 橢圓型的迭代后得到的零點不趨于邊界, 不能構(gòu)成Blaschke乘積.

1 定理1的證明

命題1單位圓盤上的解析自同構(gòu)中, 所有拋物型的和雙曲型的在迭代后得到的零點均可構(gòu)成Blaschke乘積B1(z)和B2(z), 橢圓型的零點不能構(gòu)成Blaschke乘積.

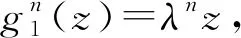
由于

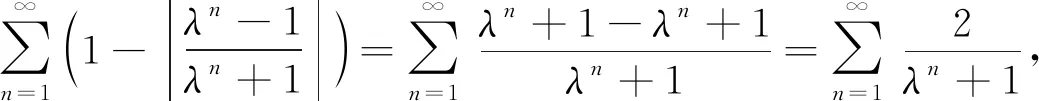
(1)

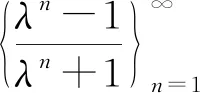
注意到

其中

設(shè)α=a+bi, 化簡得

其中

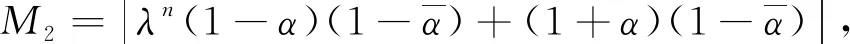
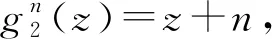
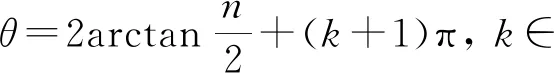
其中

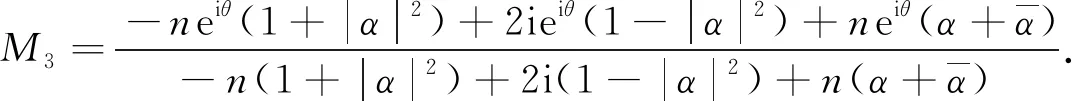
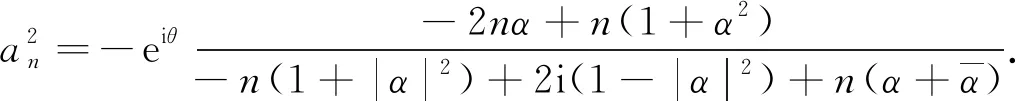
設(shè)α=a+bi, 化簡得

其中

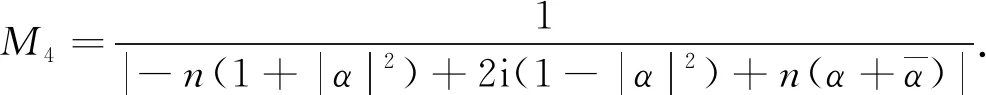
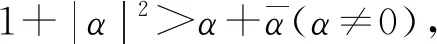
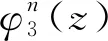
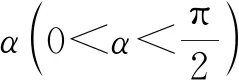
引理1[2]令b是一個零點為{zn;n∈}的插值Blaschke乘積.如果對某個σ∈(0,1), 集合是連通的, 則b即為一個單分支的內(nèi)函數(shù).特別地, 如果對所有的n, 均有ρ(zn,zn+1)<σ<1, 則b也是一個單分支的內(nèi)函數(shù).

命題2B1(z)是插值Blaschke乘積并且是單分支的.

其中

因此零點收斂, 極限點為-eiθeiβ.

此時,

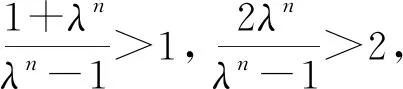
當cosm<0時, ?N, 使得當n>N時, |λn-1|>λn-1, 則有

引理2[2]如果Blaschke乘積的零點zn=rneiθn滿足:

rn

則該Blashke乘積是插值的且是單分支的.

命題3B2(z)是插值Blaschke乘積并且是單分支的.

因此不妨設(shè)

則

并且有

其中

由引理2知,B2(z)是插值的且是單分支的.

綜合命題1～命題3可得定理1.