“虛擬教室與教學樓”模型在無機化學四個量子數教學中的應用
陳廣慧,林旺強,馬荔
1汕頭大學理學院化學系,廣東 汕頭 515063
2上海交通大學化學化工學院,上海 200240
1 課程調研
無機化學[1]是化學專業大一本科生的必修課。根據多年的教學經驗,發現其中許多學生對主量子數n、角量子數l、磁量子數m和自旋磁量子數ms這四個量子數的概念及其物理意義不理解,影響了后續內容,如亞層原子軌道的能量比較、核外電子的排布、元素各論知識的學習。為了解學生陷入困境的原因,我們進行了課程調研,探究是什么原因導致對以上內容理解困難。最后,根據學生的反饋,總結出以下兩點原因:
(1) 大部分學生在高中階段原子結構與性質相關知識的缺失。廣東高校的大部分生源均來自于廣東省,高考使用的是全國I卷,其中原子結構與性質的內容不是必考,只需從兩道選考題,即有機化學基礎和原子結構與性質中任選一道答題即可。因為有機化學基礎選做題相對比較簡單,相對容易得分,所以廣東省內的大部分高中都建議或引導學生專攻有機化學基礎的選做題,甚至不少高中直接放棄原子結構與性質的內容。只有少數重點高中為了取得優異的競賽成績,針對有機化學基礎和原子結構與性質的內容安排課時進行學習。因此,導致大部分高中學生對于原子結構的知識還停留在初中階段,認為核外電子只是單純地繞原子核做圓周運動,完全沒有掌握亞層軌道、電子自旋這些基本概念。由于高中原子結構與性質相關知識的缺失,這部分學生初到大學,以前學習的知識體系突然被顛覆,面對無機化學課程,特別是原子結構與性質的內容就會束手無策,覺得難懂、難學。
(2) 學生還沒適應大學學習的抽象思維。高中的大部分知識都非常具體,著重學習現象與結論,例如A和B反應生成C和D并伴隨著怎樣的實驗現象,對于反應機理或物質內在結構的學習只是停留在皮毛階段。然而大學著重學習原理和結構與性質內在的聯系,需要具備抽象的思維來理解原理。而大一學生剛從高中畢業,還沒有具備大學化學專業課學習所必需的抽象思維能力。
根據以上調研可以發現,無機化學課程是化學類專業大一新生踏入大學的第一門專業課,教師在教學中需要深入了解學生現有的知識水平,對接高中的知識,盡量想辦法把抽象的概念具象化,并在教學中逐漸培養學生的抽象思維,這是對無機化學課程教師的一大挑戰。
研究表明[2],學生在學習的過程中看到陌生概念和規律時,總是不斷在大腦中搜索與此相關的信息,再根據相關信息進行篩選和處理。當發現新問題與舊知識有相似點時,會進行比較和推測,使用類比法正是遵循這個過程。類比的一個重要特征就是用一個熟悉的事物去說明陌生的事物,用淺顯的事理來說明復雜抽象的事理,達到其他邏輯推理方法所不能達到的目的。因此,使用類比法不僅遵循學生的學習規律,同時也能鍛煉學生的創造性思維能力。所以,類比教學對教育的改革和發展有著重要的實踐意義。
采用類比法教學使課程中抽象的概念具象化,很多高校化學教師積累了成功的經驗。例如郭玉鵬[3]使用類比法應用在物理化學熱力學函數關系式的教學中,幫助學生記憶復雜的熱力學函數關系式,最終幫助學生提高學習效果。楊風霞和連照勛[4]采用公式類比、模型類比、概念類比和判據類比的方法對物理化學知識進行總結與歸納,便于學生掌握和復習。黃四平等[5]將類比思維應用于有機化學教學中,有效地提高教學效果和學生的學習效果,拓寬學生的知識視野、培養學生的創新思維。唐正姣等[6]將類比教學應用于化工原理課程中,引導學生使用類比法解決填料吸收塔與板式精餾塔的計算問題,達到提高教學效果的目的。借鑒他們的成功經驗,我們也嘗試將類比法應用于無機化學物質結構內容的教學中,將抽象的概念具體化、形象化,希望通過類比教學能使學生對四個量子數的概念有深入的理解和掌握。
2 四個量子數的物理意義
進行類比法教學前,需要理解四個量子數的由來:推導和求解單電子原子的薛定諤方程(Schr?dinger equation)[7],如式(1)所示:



式中me與mN分別為電子和原子核的質量。因此,將式(2)代入式(1)即可得到單電子原子的薛定諤方程,如式(4)所示:

實驗證明,使用分辨率較強的分光鏡觀察氫原子光譜時,當電子由2p軌道躍遷到1s軌道時得到的不是一條譜線,而是靠得很近的兩條譜線。這一現象不能用n,l,m三個量子數進行解釋。因為2p和1s從n,l,m三個量子數的角度來看都只是一個能級,這種躍遷只能產生一條譜線。1925年兩位荷蘭學生烏倫貝克(George Eugene Uhlenbeck)和古德斯密特(Samuel Abraham Goudsmit)根據氫原子和堿金屬光譜的精細結構等諸多實驗事實[11],發展了行星模型,提出電子不僅有軌道運動、還有自旋運動具有自旋角動量這一假說。自旋角動量在磁場方向的分量Msz由自旋磁量子數ms決定[12],如式(5)所示:

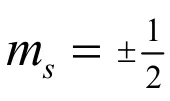
根據以上單電子原子薛定諤方程的求解即可得到四個量子數的物理意義。主量子數n是描述原子中電子出現概率最大區域離核的遠近[1]。n= 1,代表第一層,這是離核最近的電子層;n= 2,代表第二層;n= 3,代表第三層。因此,n值是量子化的,n值越大代表電子離核越遠,能量越高。對于單電子的氫原子和類氫離子來說,主量子數n決定了電子的能量;對于多電子原子或離子,核外電子的能量除了取決于主量子數n以外,還與其他因素有關,如角量子數l。
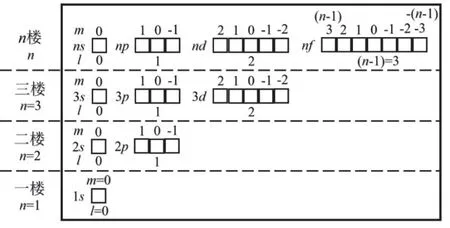
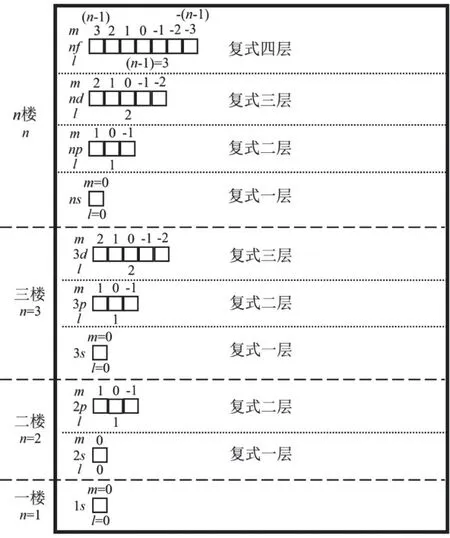
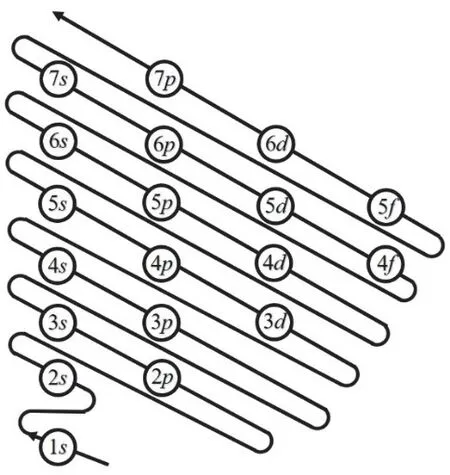
角量子數l的取值為0,1,2,3,4,…,(n? 1),分別用符號s,p,d,f,g來表示。因此,l的取值受主量子數n的限制,只能取從0到(n? 1)的整數,共有n個值。角量子數l的物理意義是代表原子亞層軌道的形狀。l= 0,表示s軌道,形狀為球形;l= 1,表示p軌道,形狀為啞鈴形;l= 2,表示d軌道,形狀為花瓣形;l= 3,表示f軌道,形狀更復雜。對于多電子原子或離子來說,其能量由主量子數n和角量子數l共同決定[13]。對于n相同,l不同的原子軌道,l越大軌道能量E越大,例如E4s 磁量子數m的取值為0,±1,±2,±3,±4,…,±l,即m的取值受角量子數l的影響,從0到±l,共有(2l+ 1)個取值[14]。磁量子數m的物理意義是決定原子軌道在核外空間中的取向[8]。當角量子數l=0時,表示球形的s軌道,這時磁量子數m只有一種取值0,因此s軌道在核外空間中只有一種分布方向,即以核為球心的球形分布;l= 1時,表示啞鈴形的p軌道,m有三種取值0和±1,說明p軌道在核外空間坐標系有三種不同的分布方向。一般情況下,磁量子數m與原子軌道的能量無關,因此三種不同取向的p軌道,其能量相等;l= 2時,表示花瓣形的d軌道,m有五種取值0,±1和±2,說明在核外空間中有五種不同的分布方向,這5種d軌道能量簡并,即簡并度為5。 綜上所述,n,l,m這三個量子數可以決定原子軌道的離核遠近、形狀和空間取向,而ms則決定電子的自旋方式。因此,四個量子數確定之后,電子在核外空間的運動狀態就確定了。 如果將以上抽象的知識直接向剛進大學的大一新生進行講授,學生一時肯定難以接受新概念和新知識,例如原子軌道代表原子體系單電子波函數等概念。因此,為了幫助學生越過抽象思維的“能壘”,我們先采用類比教學的方法向學生構建“虛擬教室與教學樓”模型將四個量子數的概念及其物理意義具象化。 對于單原子或離子,如氫原子或者類氫離子,無論主量子數n等于多少,原子亞層軌道的能量都相同,即Ens=Enp=End=Enf。因此,我們向學生構建出“虛擬教室與教學樓”模型,如圖1所示,用來說明四個量子數的概念。將電子比作學生,樓層比作電子層,樓層中的復式比作電子亞層,一間教室比作一個原子軌道。當n= 1時,只有1個s軌道,對應教學樓一樓只有一間教室,教室里面有兩位學生,一位學生面向黑板,另一位學生背向黑板,代表1s軌道有兩個自旋相反的電子;n= 2時,對應教學樓二樓有四間教室,分別是一間2s教室和三間2p教室,每間教室有兩個坐向相反的座位;同理,n= 3時,教學樓三樓有一間3s教室、三間3p教室和五間3d教室,每間教室有兩個坐向相反的座位。n≥ 4的情況也是以此類推。 圖1 單電子體系“虛擬教室與教學樓”模型 對于多電子原子或離子,結合圖2“虛擬教室與教學樓”模型進行類比教學。n= 1時,只有1個s軌道,對應教學樓一樓只有一間教室,教室里面有兩位坐向相反學生,代表1s軌道填充兩個自旋相反的電子;n= 2時,有1個2s軌道和3個2p軌道,對于多電子原子或離子2p軌道的能量大于2s軌道,因此我們將復式樓層比喻為電子亞層:教學樓二樓是二層復式樓層,復式一層只有一間教室,代表2s軌道,教室里有兩個坐向相反的座位,代表可容納兩個自旋相反的電子;復式二層有三間教室,代表2p三個能量簡并的軌道,每間教室里面有兩個坐向相反的座位,復式二層共4間教室,教室數等于n2(n= 2);同理,n= 3時,教學樓三樓是三層復式樓層,復式一層只有一間教室,二層有三間教室,三層有五間教室,復式二層共9間教室,教室數等于n2(n= 3);n≥ 4的情況也是依此類推。 與此同時,我們在講授時特別強調主量子數、角量子數與磁量子數間的約束關系,如圖1、圖2所示:例如對于多電子體系,教學樓的樓層數等于主量子數,每一樓層的復式層代表電子亞層,也即代表角量子數,因此樓層數與復式層數的數量關系,也就是主量子數與角量子數的約束關系,每一層復式有若干教室,教室數目代表磁量子數,即復式層數與教室數的關系,也代表著角量子數與磁量子數的約束關系。 圖2 多電子體系“虛擬教室與教學樓”模型 另外,我們也利用“虛擬教室與教學樓”模型向學生講授電子排布的三大規則:能量最低原理、泡利不相容原理和洪特規則,引導學生掌握1–18號元素的電子排布規律。 在課堂上采用以上類比教學,大部分學生對四個量子數的概念及其物理意義在頭腦中產生了清晰的圖像,也初步地理解了1–18號元素的電子排布規律,說明我們類比教學取得理想的成果。但是單憑以上的知識,學生還不足以完全掌握其他基態原子的電子排布。對于多電子原子,原子軌道徑向分布的不同,導致了屏蔽效應和鉆穿效應的出現,引起了多電子原子能級交錯的現象。例如原子序數為15–20的元素,E4s 圖3 電子填充能級順序圖 最后,為了檢驗本次教學改革的效果,我們進行了隨堂測驗,考查1–36號的元素的基態原子的電子排布。發現與往年相比,學生都普遍獲得較好的成績,說明采用這種類比教學方法取得滿意的效果。說明這種把抽象的概念具象化、形象化的類比教學法取得了成功。同時,我們在無機化學后續內容的教學中逐漸加強培養學生的抽象思維。 提出問題:一直以來,不少學生反映無機化學課程的物質結構部分難學難懂,特別是覺得四個量子數非常抽象而學得一知半解,導致對后續的內容完全不知所云。 解決問題:為了幫助學生解決這一難題,我們采用類比教學的方法將抽象的四個量子數的內容具象化——利用“虛擬教室與教學樓”模型進行類比,將電子比作學生,樓層比作電子層,樓層中的復式比作電子亞層,一間教室比作一個原子軌道,將看不見摸不著的抽象概念形象化、簡單化。同時,向學生推薦使用類比法將抽象的內容具體化,能幫助學生培養抽象思維,幫助學生適應大學的學習。 課后反響:通過學生的課堂表現與隨堂測驗的結果,發現學生的理解和掌握程度比往年都要理想,說明當前的類比教學取得理想的教學效果。這也激勵我們今后將類比教學方法運用于更多的知識點教學上,幫助學生理解得更深入,掌握得更扎實。同時也希望學生能夠將類比思維應用于日后的學習與科研之中。 不足:“虛擬教室與教學樓”模型也存在其不足之處: (1) 未能強調自旋并無經典的可對應量; (2) 未能體現洪特規則; (3) 沒法解釋屏蔽效應和鉆穿效應帶來的多電子原子軌道能級交錯; (4) 該模型使用是否為復式樓層去類比單電子與多電子體系,實際上,原子或分子體系是不分單電子或多電子體系,兩者應是統一自洽的,本模型并沒有建立一個更完善的模型去統一描述單電子與多電子體系,這是本模型的缺點。但是如果建立這樣的模型,勢必需要引入介紹更深奧難懂的概念,例如兩個電子之間的交換相關作用等,只會增加學生的理解難度。如果我們講授的是本科高年級課程結構化學,甚至是研究生課程量子化學,引入更深奧的概念去構建更完善的模型是很有必要的。但我們的初衷只是為了讓剛踏入校園的大一新生掌握四個量子數的物理意義以及其能級的能量高低,才使用“虛擬教室和教學樓”模型進行類比,如果引入更深奧的理論去構建更完善的模型,我們認為這是不切實際的,學生肯定很難理解和接受。當然,我們在講授的過程中會以思考題的形式讓學生尋找該模型的缺點,最后我們肯定也會在講授過程中強調其中的缺點,以防學生進入理解誤區。 這是當前“虛擬教室與教學樓”模型的不足,這也是在后續的教學實踐中需要提高與改進之處。在這里拋磚引玉,希望能跟同行進行交流并改進。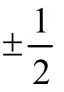
3 四個量子數的類比教學
4 結語

