d-作用下保測(cè)系統(tǒng)的限制敏感性
張瑞豐, 朱曉凡
(合肥工業(yè)大學(xué) 數(shù)學(xué)學(xué)院,合肥230601)
1 引 言
1948年,Shannon將統(tǒng)計(jì)物理中的概念引申到通道通信的過(guò)程中時(shí)提出了Shannon熵的概念,開創(chuàng)了“信息論”.隨后,1959年,Kolomogorov和Sinai借助Shannon信息論中的思想,引入了測(cè)度熵的概念,首次將熵與動(dòng)力系統(tǒng)結(jié)合起來(lái).之后Adler,Konheim和McAndrew于1965年在拓?fù)鋭?dòng)力系統(tǒng)中用開覆蓋定義了連續(xù)映射的拓?fù)潇?1971年,Bowen利用分離集和張成集給出了拓?fù)潇氐牡葍r(jià)定義.
1971年,Ruelle[1]首次嚴(yán)格的給出了初值敏感依賴的定義,受到人們的廣泛關(guān)注.1986年,Devaney把初值敏感依賴作為定義動(dòng)力系統(tǒng)混沌的重要條件,給出了比Li-Yorke混沌更直觀的定義——Devaney混沌.熵和敏感性都是反映系統(tǒng)復(fù)雜程度的重要指標(biāo),敏感性和熵之間的關(guān)系也一直是專家學(xué)者感興趣的研究方向.2005年Cadre和Jacob在文獻(xiàn)[2]給出了兩兩敏感的概念,并說(shuō)明弱混合蘊(yùn)含兩兩敏感,同時(shí)證明了正熵蘊(yùn)含兩兩敏感.之后,2012年,Domenico Aiello和Hansheng Diao[3]在其基礎(chǔ)上給出了限制敏感性和限制兩兩敏感的定義,并研究了限制敏感性、限制兩兩敏感性與測(cè)度熵之間的關(guān)系.
2 準(zhǔn)備知識(shí)
Λn={g=(g1,g2,…,gd)∈d∶|gi| λn=#Λn,#Λn代表集合Λn中元素個(gè)數(shù). 定義1[6]設(shè)(X,B,μ)是一個(gè)概率空間,G為作用在空間上的d-作用,若對(duì)?g∈Λn和?B∈B,都有 g-1B∈B且μ(g-1B)=μ(B), 則稱(X,B,μ,d)是一個(gè)保測(cè)系統(tǒng). 定義2[6]設(shè)(X,B,μ,d)是一個(gè)保測(cè)系統(tǒng),如果對(duì)任意?g∈Λn滿足g-1B=B的B∈B,必有μ(B)=0或μ(B)=1,那么稱系統(tǒng)(X,B,μ,d)是遍歷的. 定義3[6]設(shè)(X,B,μ)是一個(gè)概率空間,μ∈M(X),G為作用在空間上的d-作用A={A1,A2,…,Ak}是一個(gè)有限可測(cè)剖分,定義剖分A測(cè)度熵為 進(jìn)一步定義G關(guān)于剖分A的測(cè)度熵為 定義G關(guān)于μ的測(cè)度熵為 hμ(G)=suphμ(G,A), 這里A取遍X所有有限可測(cè)剖分. 定義4(X,B,μ,d)是一個(gè)保測(cè)系統(tǒng),ρ是X上與測(cè)度μ相容的度量.如果對(duì)μ-a.e.x∈X,存在δ>0,a>0,使得對(duì)所有ε>0,存在n∈,及存在g∈Λn有 μ{y∈Bε(x)∶ρ(gx,gy)>δ}>0, 則稱(X,B,μ,d)是限制敏感的. 定義5(X,B,μ,d)是一個(gè)保測(cè)系統(tǒng),ρ是X上與測(cè)度μ相容的度量.如果存在a>0,δ>0使得對(duì)μ×μ-a.e.(x,y)∈X×X,存在n∈,及存在g∈Λn使得 ρ(gx,gy)>δ, 則稱(X,B,μ,d)是限制兩兩敏感的. 稱δ為敏感性常數(shù),a為漸進(jìn)率,根據(jù)定義,如果δ為敏感性常數(shù),則任意δ′<δ也是敏感性常數(shù);如果a為漸進(jìn)率,則任意a′>a也是漸進(jìn)率. 性質(zhì)1設(shè)(X,B,μ,d)是一個(gè)保測(cè)系統(tǒng),ρ是X上與測(cè)度μ相容的度量,且ρ是μ-正則的,如果(X,B,μ,d)是限制兩兩敏感的,則其也是限制敏感的. 證假設(shè)(X,B,μ,d)是有限制兩兩敏感常數(shù)δ和漸進(jìn)率a的限制兩兩敏感的,由定義可知對(duì)a.e.x∈X,a.e.y∈X,存在n∈,及?g∈Λn,使得ρ(gx,gy)>δ. 因?yàn)棣咽铅?正則的,對(duì)上述x,取c>0,使得 (1) 考慮對(duì)任意ε≤δ,εΜ=sup{ε′<ε∶μ(Bε′(x))<μ(Bε(x))}.若μ(BεM(x))=μ(Bε(x)),則取ε′<εM非常接近εM,使得 μ(Bε(x)Bε′(x))>0,μ(Bε′(x))≥cμ(Bε(x)). (2) μ(Bε(x)Bε′(x))>0. 根據(jù)(1)式可得 (3) 根據(jù)上述x和ε′,對(duì)a.e.y∈Bε(x)Bε′(x),存在n∈,及?g∈Λn,有ρ(gx,gy)>δ. 由(2),(3)式可知 μ(Bρ(x,y)(x))≥μ(Bε′(x))≥cμ(Bε(x)), 故 所以(X,B,μ,d)限制敏感的. 性質(zhì)1說(shuō)明了在ρ是μ-正則的情況下,限制兩兩敏感性比限制敏感性強(qiáng).敏感性和熵都是反映動(dòng)力系統(tǒng)復(fù)雜程度的量,自然地,想要研究敏感性與熵之間的關(guān)系.文獻(xiàn)[7]中給出了amenable群作用系統(tǒng)下非遍歷情形的Shannon-McMillan-Brieman定理,amenable群包括所有的有限群,緊致群和可解群,d是一類特殊的amenable群. 引理1(Shannon-McMillan-Brieman定理:非遍歷情形) 設(shè)(X,B,μ,d)為一個(gè)保測(cè)系統(tǒng),G為一個(gè)可數(shù)離散amenable群,對(duì)G中任何滿足增長(zhǎng)條件的temperedFφl(shuí)ner序列{Fn}以及X的有限可測(cè)剖分P,對(duì)μ-a.e.x∈X都有 且 定理1設(shè)(X,B,μ,d)是一個(gè)保測(cè)系統(tǒng),μ是X上的無(wú)原子概率測(cè)度,ρ是X上與測(cè)度μ相容的度量,且是μ-正則的,令A(yù)={A1,A2,…,Ak}是X的一個(gè)有限可測(cè)剖分使得對(duì)所有?i有diamAi<δ,令hμ(G,A)是G關(guān)于剖分A的測(cè)度熵.如果(X,B,μ,d)是有漸進(jìn)率a和限制兩兩敏感常數(shù)δ的限制兩兩敏感的,則有 證假設(shè)(X,B,μ,d)是有限制敏感常數(shù)δ和漸進(jìn)率a的限制兩兩敏感的,由定義知:選x∈X使得對(duì)μ-a.e.y∈X,存在n∈,及?g∈Λn使得 ρ(gx,gy)>δ. (4) ρ(gx,gy)<δ, ?g∈Λn (5) 由于ρ是μ-正則的,存在c>0使得 因?yàn)棣淌菬o(wú)原子概率測(cè)度,故當(dāng)r→0時(shí),μ(Br(x))→0.對(duì)任意的整數(shù)n,令εn滿足 e-(n-1)c>μ(Bεn(x))≥e-nc. 于是 兩邊取對(duì)數(shù)得 即 由題設(shè)可知(X,B,μ,d)是有限制敏感常數(shù)δ和漸進(jìn)率a的限制兩兩敏感的,則存在 及存在g∈Λi,使得ρ(gx,gy)>δ.由(5)可知y?Cn(x),斷言得證. 故由斷言得 令 由Shannon-McMillan-Brieman定理 定理1說(shuō)明了對(duì)于一個(gè)保測(cè)系統(tǒng)來(lái)說(shuō),限制兩兩敏感意味著正測(cè)度熵,自然地,想要知道限制敏感與熵之間的關(guān)系.在證明定理2的過(guò)程中要用到文獻(xiàn)[8]中的amenable群作用下遍歷版本的 Brin-Katok熵公式: 其中BFn(x,ε)={y∈X∶ρFn(x,y)<ε}={y∈X∶ρ(gx,gy)<ε,對(duì)任何g∈Fn}. 定理2設(shè)(X,B,μ,d)是一個(gè)遍歷系統(tǒng),μ是無(wú)原子概率測(cè)度,ρ是X上與測(cè)度μ相容的度量.如果則對(duì)所有x∈X,(X,B,μ,d)是有漸進(jìn)率a和敏感常數(shù)δ的限制敏感的. 證假設(shè)對(duì)所有x∈X,(X,B,μ,d)不是有漸進(jìn)率a和敏感常數(shù)δ的限制敏感的.存在一個(gè)正測(cè)集A,使得對(duì)?x∈A和δ>0,存在ε(δ)≤δ,對(duì)所有n∈,及?g∈Λn,有 μ{y∈Bε(δ)(x)∶ρ(gx,gy)>δ}=0, (6) 對(duì)這樣的n,令 ρn(x,y)∶=max{ρ(gx,gy)∶?g∈Λn},Bn(x,δ)={y∈X∶ρn(x,y)≤δ}, ρ(gx,gy)≤δ, ?g∈Λn (7) 故 利用Brin-Katok熵公式,存在x∈A使得 與已知條件矛盾,假設(shè)不成立,所以對(duì)所有x∈X,(X,B,μ,d)是有漸進(jìn)率a和敏感常數(shù)δ的限制敏感的. 致謝非常感謝相關(guān)文獻(xiàn)對(duì)本文的啟發(fā)以及審稿專家提出的寶貴意見.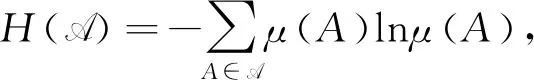
3 主要結(jié)果及證明

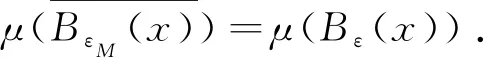

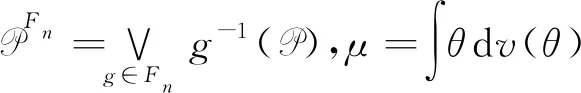
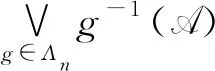

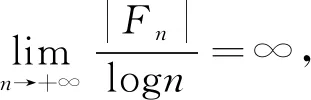


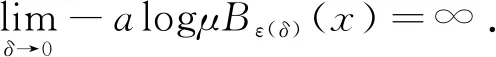
4 結(jié) 論

