大學數學公共課程思政元素挖掘初探

趙東紅， 魏海瑞， 劉 林

(北京科技大學 數理學院，北京100083)

1 引 言

為了深入貫徹落實習近平總書記關于教育的重要論述和全國教育大會精神，全面落實“三全育人”精神，2020年5月28日教育部印發了《高等學校課程思政建設指導綱要》.《綱要》指出，全面推進高校課程思政建設，把思想政治教育貫穿人才培養體系，將課程思政融入課堂教學建設全過程. 大學公共數學課程思政育人目標是注重數學思維方法訓練和科學倫理教育，培養學生探索未知、追求真理、勇攀科學高峰的責任感和使命感，在向學生傳授課程知識的同時，使其樹立正確的價值觀，激發學生科技報國的家國情懷和使命擔當. 樹立“課程思政”理念，強調學校教育應具備360度德育“大熔爐”的合力作用[1]，立足大學數學教學內容，將德育與數學基礎知識融于一體，借助知識點、數學史、典故等，將知識傳授與價值引領相結合，引導學生正確做人、做事和做學問，助力學生全面發展，報效祖國，實現“立德樹人”之根本目標. 近幾年，一線數學老師對數學專業課程進行了思政元素融入課程的研究——朱婧等[2]在《數學模型》將思政元素融入到傳染病模型教學中，劉秀琴等[3]在《隨機過程》將思政元素融入到馬爾可夫鏈的講解過程中，公徐路[4]以《離散數學》課程的思政教育為出發點，將德育元素合理滲透到專業知識中，鄭蘇娟等[5]以河海大學大禹學院《工科數學分析》這門課程為例研究了如何融入思政元素，提出了四要素，并將思政教育融于拔尖創新人才的培養體系中，取得了一定的成效，閔杰等[6]提出了《數值分析》課程思政建設的七個方面內容，并分別給出課程思政的教學案例. 同樣，公共數學課程進行了融入思政元素到課程教學的研究—吳慧卓[7]以《高等數學》為例，闡述了課程思政的內涵，以實現從思政課程到課程思政的轉化，孫和軍等[8]結合數學學科特點和課程育人定位，設計切合實際的思政映射和融入點，選擇合適的教學手段和方法，無痕地將思政元素融入課程教學. 但是，公共數學課程思政元素融入更偏重于理論描述，主要是在思政研究的必要性等方面.本文主要是從思政元素與實際案例的結合為出發點，研究公共數學課程思政元素融入，更加具體，更加直觀，而且教學實踐反映了以思政融入為契合點的教學內容更新，教學設計變化的成效.

最后設計科學的調查問卷，通過分析數據，可以看到在教務評價系統中，同學們對思政元素融于教學內容的反饋取得了令人滿意的成效. 最終初步實現了適合各工科專業的公共數學課程內容重整，教學設計更新，人文教育滲透，把整個公共數學課程的教學質量提高一個臺階.

本文立足于思政微案例，對課程思政教學模式進行設計，但由于篇幅限制，只是對公共數學課程思政元素進行分析，分別對微積分、線性代數、概率論與數理統計挖掘思政元素，闡述并進行舉例和初探.

2 主要內容

2.1 微積分課程思政元素挖掘并舉例

以極限、定積分物理應用、常數項級數為例,詳細地分析了思政元素的結合點，增強了數學學習的趣味性，實現借助合適的思政結合點幫助同學們樹立正確的人生觀和價值觀.

思政微案例1極限——自然對數底e

金融復利問題：按年、半年、季度、月、周和天的順序，計算一年后本息和，見表1.

表1 復利計息

(i) 繼續按照小時、分鐘和秒計息，假設計息周期趨于零，一年后本息會一直增大嗎？

(iii) 引入e后,介紹歷史上對e的研究過程[10]，約翰·納皮爾找到了對數常數e；歐拉證明了e是無理數；夏爾·埃爾米證明了e是超越數.

無論是金融利滾利問題引入，還是對e的拓展學習，極大地提高了學生對數學的濃厚興趣，同時讓同學們更加理解，現在課本中學習的每一個知識點離不開一代代科學家不懈努力和刻苦鉆研.

思政微案例2定積分物理應用——變力做功

設墻壁對鐵釘阻力與鐵釘擊入深度成正比，鐵釘長6cm，每次將鐵釘擊入1.5cm，如果鐵錘每次擊打鐵釘時做功相等，鐵錘擊打多少次能將鐵釘完全釘入?

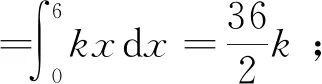
此例有助于同學們深刻理解習近平總書記的“發揚釘釘子的精神，一張好的藍圖一干到底”[11]涵義，實現培養學生學習和工作中要有專心致志和刻苦鉆研精神的育人目標.

圖1 變力做功

思政微案例3常數項級數——芝諾悖論

芝諾認為阿基里斯永遠追不上烏龜，原因是：假設剛出發時，阿基里斯在A點，烏龜在B點，經過一段時間之后他到了B點，而烏龜卻也往前走了一段到達了C點；阿基里斯又從B點開始追，等到達C點時，烏龜又往前走了一段，到了D點……總之，阿基里斯每趕到烏龜之前的落腳點，烏龜就已經往前走了一段，雖然它們之間距離永遠在縮小，但他永遠追不上烏龜！

圖2 芝諾悖論

芝諾悖論是缺少微積分這一數學工具造成錯誤理解，無法處理“無窮個無窮小”總和是什么.當每階段考慮的時間越來越小，成為一個收斂的無窮級數，實際上證明了阿基里斯落后于烏龜的時間是有限的,并將在有限的時間內超過烏龜.

圖3 液膜冷卻問題

這個悖論對于鍛煉同學們的數學思維有很重要的意義.芝諾悖論和其他邏輯學上有趣的悖論一次又一次地提醒哲學家和邏輯學家們去反思自己的思維框架和習慣，人類就是在這種反思和檢討中戰勝錯覺，取得進步.

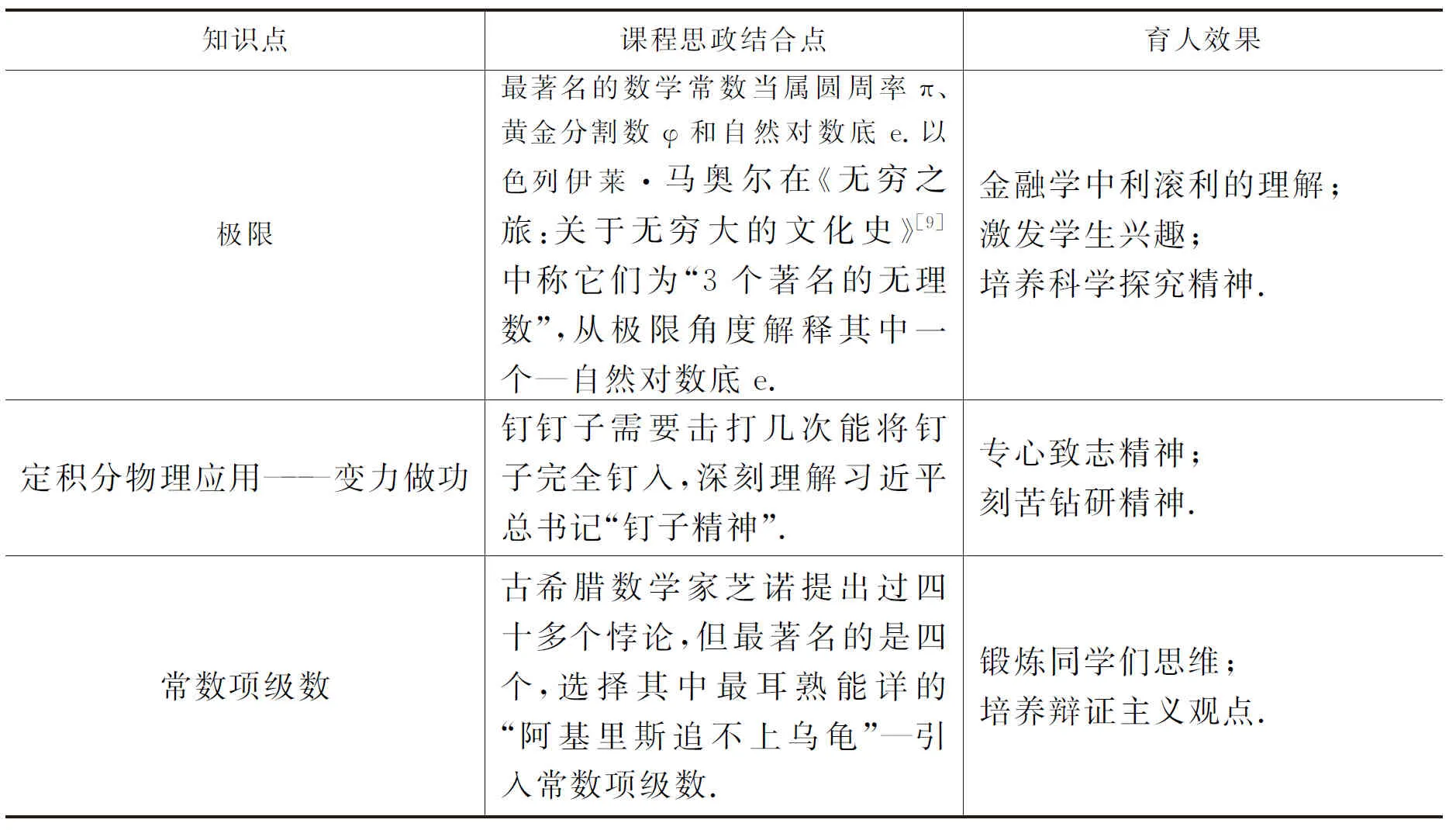
表2 微積分思政元素挖掘舉例

2.2 線性代數課程思政元素挖掘并舉例

公共數學課中線性代數特點是公式多、式子大、符號繁瑣以及規律性強，思政元素挖掘比較困難，下面以基變換與坐標變換、矩陣對角化、線性方程組為例，對思政元素進行分析.

思政微案例1基變換和坐標變換——液膜冷卻問題

從中國航天衛星發射的歷史進程引入，重點以長江二號火箭為例，介紹助推器發動機和一級主發動機的構成，引出液膜冷卻問題.

這個實例既能形象直觀地把基變換和坐標變換引出，又能激發同學們的愛國主義熱情. 在引入過程中，同學們一起回顧了中國航天事業發展歷程，充分肯定了祖國發展成就，增強了青年學生民族自豪感.雖然只是一節普通的數學課，但是很好地融合了思政材料，整個融入過程非常流暢，不但使同學們獲得了數學知識，而且提高了思想境界，取得了一定的思政育人成效.

思政微案例2矩陣對角化——人口問題

假設北京市總人口是固定的，若每年有5%居民搬到郊區，3%郊區居民搬到市區，假設初始人口情況如下：40%居住在市區，60%居住在郊區，問10年、40年、60年后，市區和郊區人口比例如何?

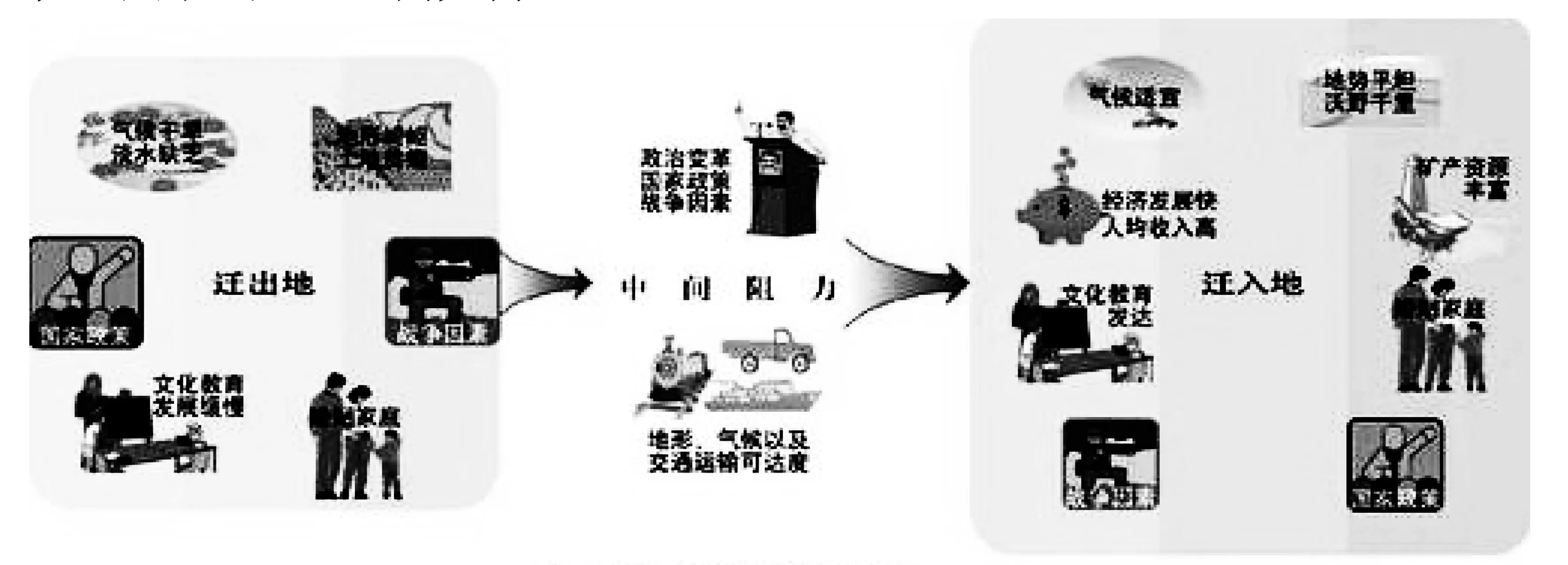
圖4 人口遷移

作為開放式作業，通過矩陣對角化解決矩陣冪運算. 一方面有助于理解如何將抽象的知識點通過數學建模應用到實際問題中，另一方面引起同學們對城市問題、生態環境問題和人口遷移問題等社會問題的重視，引導同學們關注社會發展和民生問題，深刻理解新時代大學生歷史使命和責任擔當[12].

思政微案例3線性方程組——《九章算術》

《九章算術》第八章方程中介紹了一次方程組，采用分離系數方法表示方程組，這些系數相當于現在的矩陣. 解方程組使用的直除法與矩陣的初等變換一致，這是世界上最早提出的完整解線性方程組解法. 在這一章使用了負數，雖然負數是現在初一年級學習的內容，但在當時這是世界數學史上一項重大成就，第一次突破了正數范圍，拓展了數字系統.

表3 線性代數思政元素挖掘舉例

2.3 概率論與數理統計課程思政元素挖掘并舉例

概率論與數理統計[13]相對于其他公共數學課程而言，跟實際問題結合最為密切，應用背景更豐富，本文從課堂教學挖掘的思政元素中，以數學期望、貝葉斯公式、假設檢驗為例進行分析.

思政微案例1數學期望——核酸檢測分組

原問題：某地區共有1000人參加疾病普查，已知每人血液呈陽性的概率是0.2，采用兩種方案進行血液檢測.

方案1：逐一進行檢測；方案2：每100人為一組進行分組檢測，哪種方案最優？

新問題：某地區共有1000人參加新冠病毒核酸檢測，已知每人咽拭子呈陽性的概率是0.2，采用兩種方案進行核酸檢測.

方案1：逐一進行檢測；方案2：每100人為一組進行分組檢測，哪種方案最優？

這一背景變化結合了當前實際環境，本質上是同一個數學問題——數學期望，不同的是給我們提供了非常好的思政育人條件，在課堂教學中計算出結果之后，設計了一個分享最近一年感受的環節，可以看出每個同學不但學業上取得進步，思想上更加成熟.

思政微案例2貝葉斯公式——警察破案

某地發生了一個案件，嫌疑人有甲、乙、丙三人，在不了解案情細節(事件B)之前，偵破人員根據過去的前科，對他們作案可能性有一個估計，設為P(A1)、P(A2)、P(A3),且P(A1)最小，但在知道案情細節(事件B發生)后，這個估計就變為P(A1|B)、P(A2|B)、P(A3|B),但P(A1|B)最大. 原來認為作案可能性較小的甲，現在變成了重點嫌疑犯. 通過這個引例，不但加深理解貝葉斯公式的本質，而且間接地教育同學們要成為一個遵紀守法之人.

思政微案例3假設檢驗——女士品茶

這個故事最早出現在統計學家Fisher發表于1935年的著作《The Design of Experiment》，被用來描述原假設.統計學家Fisher在當年就給出了他的一套實驗方法：他調配出了八杯其他條件一模一樣而僅僅是倒茶倒奶順序相反的茶，讓女士品嘗之后告訴他哪四杯是先倒“奶”.

首先假設女士沒有這個能力(被稱為原假設)，如果女士很好地鑒別了這八杯茶，那就說明在原假設成立的情況下，發生了非常反常的現象，以至于說明原假設是令人懷疑的.從統計上來說，如果在原假設成立的前提下，發生了非常小概率的事件，有理由懷疑原假設的真實性.這也是Fisher教授的假設檢驗的基本思路-概率性質的反證法.

這個故事作為開端，可以讓同學們理解，每一個科學理論的誕生都是來源于生活，來源于實踐，而且從中可以看到科學研究的這種精神，學習科學家善于觀察，善于對生活中的每一個細節進行思考、反思和試驗.

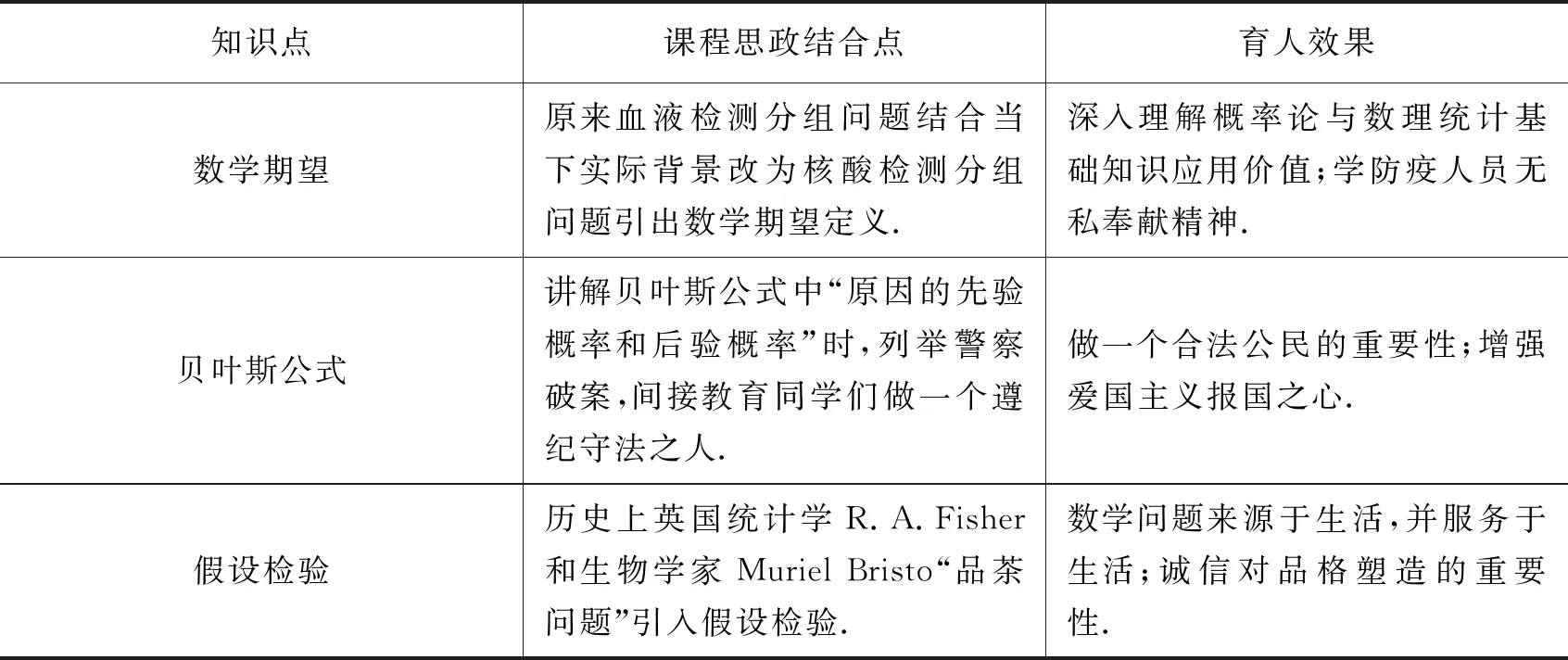
表4 概率論與數理統計思政元素挖掘舉例

3 教學效果與教學評價

3.1 教學效果

為了檢驗教學效果，學期末對微積分、線性代數兩個講臺同學進行了課程思政調查問卷.調查問卷設計了四個評價指標，分別為價值引領的作用、愛國主義與文化自信、科學創新的精神、中華民族精神，評價等級為非常有效、一般有效、無效三個層次. 微積分講臺人數151人，其中140人自愿參加了調查問卷，線性代數講臺人數180人，其中170人自愿參加了調查問卷，調查結果如圖5、圖6所示.

圖5 微積分課程思政調查數據餅圖 圖6 線性代數課程思政調查數據餅圖

實踐表明，絕大多數同學對思政元素融入到課堂教學中是肯定的，正如高教司司長吳巖所說讓課程思政成為有情有義、有溫度、有愛的教育過程. 同時說明了將思政元素融于公共數學課程內容這種教學模式值得研究和探索，我們將在今后的教學中繼續應用與改進.

3.2 教學評價

學校為落實《關于進一步加強課程思政建設的實施意見》(校黨發〔2020〕37號)文件精神，開展“課程思政特色示范課程”建設工作. 學校整個評教體系導向發生很大變化，評價內容如下：

將課程思政融入到課程教學中，提高了對學生人文關懷的程度和同學們對公共數學課程的學習興趣，可以看出學生對教師各方面評分較高，特別對課程思政有效性評價較高. 下面我們對表5中微積分講臺和線性代數講臺第2題和第7題進行詳細地分析，如圖7—圖10所示.

表5 教學評價指標數據

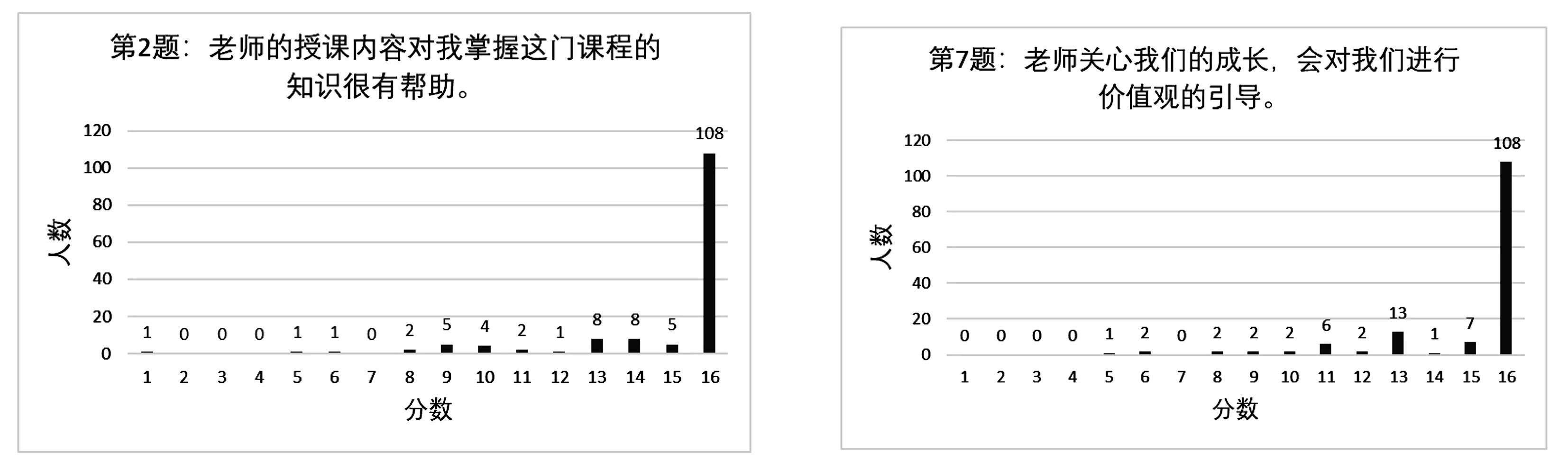
圖7 微積分講臺 圖8 微積分講臺

圖9 線性代數講臺 圖10 線性代數講臺

從上述分析中，可以看出融入了思政元素的公共數學課受到了學生認可和喜愛，但也看出個別同學覺得思政元素與課程內容融合度比較弱，說明后面我們要繼續努力挖掘思政元素，實現傳授知識與思政元素無縫對接，達到潤物細無聲的教學效果.

4 結 論

本文對三門公共數學課程思政元素挖掘并初探，從多個角度深入分析，通過豐富的教學案例說明如何將思政元素融入到課程教學中.實踐證明，公共數學思政特色示范課建設的必要性和有效性. 眾所周知，提高同學們對公共數學課程學習興趣和培養創造性思維能力是教學目標之一，現在我們更加注重如何將知識傳授，能力培養和價值引領有效結合，將隱藏在課程內容中的思政元素挖掘出來，不但激發學生的學習興趣，而且使學生具有多方面的情感、態度和價值觀，全面提升育人質量，最終實現立德樹人之根本目標.

致謝非常感謝參考文獻對本文的啟發，審稿專家認真評審了論文，提出了寶貴的意見，作者受益匪淺，在此表示衷心的感謝.