基于全參數化建模的高速客船型線優化設計

謝玲玲，張守慧，馮佰威，田中文

(1.武漢理工大學 高性能船舶技術教育部重點實驗室，湖北 武漢 430063；2.中國船級社 海南分社，海南 海口 570206；3.中船黃埔文沖船舶有限公司，廣東 廣州510715)

0 引 言

船體型線設計是船舶整體設計非常復雜和重要的部分，船舶的結構設計、性能計算、機艙布置和生產放樣均基于船體型線。通常，基于一些基本規則和相關設計經驗，針對船舶特性，確定1個或多個船體型線設計方案，通過多次模型測試改進型線并最終確定。船體型線設計通常需要手動修改，效率較低。因此，如何快速生成船體型線是船舶設計需要解決的重要問題。

基于計算流體動力學(Computational Fluid Dynamics，CFD)數值模擬方法，通過CFD數值計算尋找最佳設計方案[1-5]，該方法不僅可快速找出最佳方法，而且可更節省大量的人力、時間和試驗成本。

1 船體型線全參數化建模

采用CAESES FRIENDSHIP-Framework軟件進行全參數化建模。首先，通過分析船體型線特征，構建控制主要特征的參數化曲線；然后，根據建立的特征曲線，采用剖線生成器生成光順的橫剖線；最后，通過曲面生成器模塊Meta Surface，依據生成的剖線，采用蒙面法生成光順的船體曲面。圖1為某型高速客船全參數化模型。

圖1 某型高速客船全參數化模型

2 阻力性能數值計算

SHIPFLOW是與CEASES參數化建模軟件相結合、進行船體參數化優化應用較多的一個軟件。許多研究表明，SHIPFLOW軟件中的勢流計算和黏流計算模塊可有效求解船體阻力性能，因此選取該軟件進行水動力性能計算。

2.1 計算區域

采用SHIPFLOW軟件進行船體阻力預報，其計算區域如圖2所示。水流方向必須是由船體艏部至艉部。區域1為勢流計算區域，采用Rankine源法，按照線性和非線性的自由表面邊界條件進行高階面元法的勢流理論計算，后續的興波阻力計算主要在該區域進行。區域2為薄邊界層區域，根據邊界層理論求出邊界層厚度，對該區域船體邊界層進行計算可得到船體前部2/3的摩擦阻力[6]。區域3為黏流計算區域，包括船體后部、船體下游和整個流域尾部，采用納維-斯托克斯方程(Navier-Stokes Equations，N-S方程)、k-ε湍流模型和壁面函數進行求解。

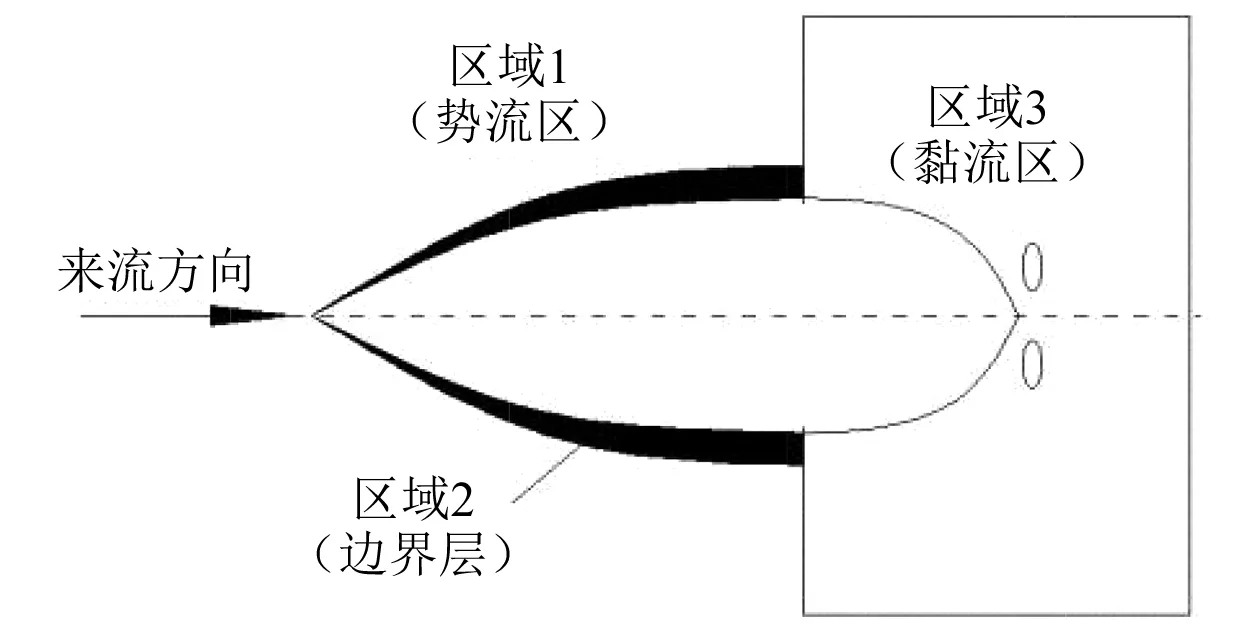
圖2 計算區域示例

2.2 CFD計算

2.2.1 計算模型

船模具體參數如表1所示。

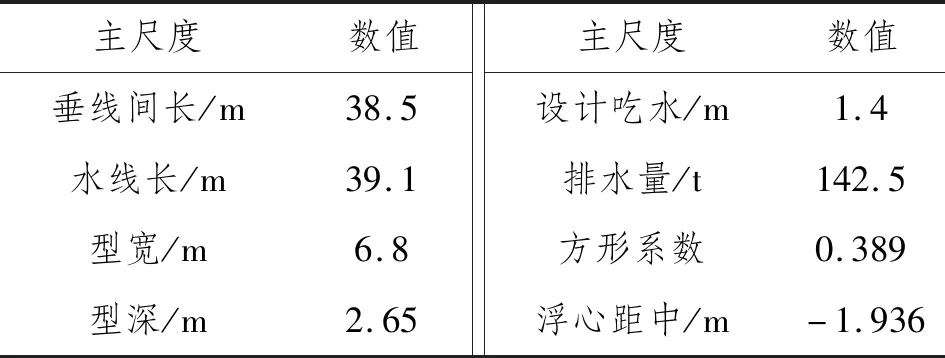
表1 船模參數

2.2.2 網格劃分

網格劃分影響后續阻力優化是否成功。SHIPFLOW軟件自帶網格劃分功能，在XMESH中進行勢流計算的面元網格劃分，在XGRID中進行黏流結構化體網格劃分。經多次設置計算，確定在進行黏流計算時采用該軟件的fine網格模式，在進行勢流計算時采用該軟件的medium網格模式。船體曲面面元網格如圖3所示。船體勢流計算網格與計算區域如圖4所示。

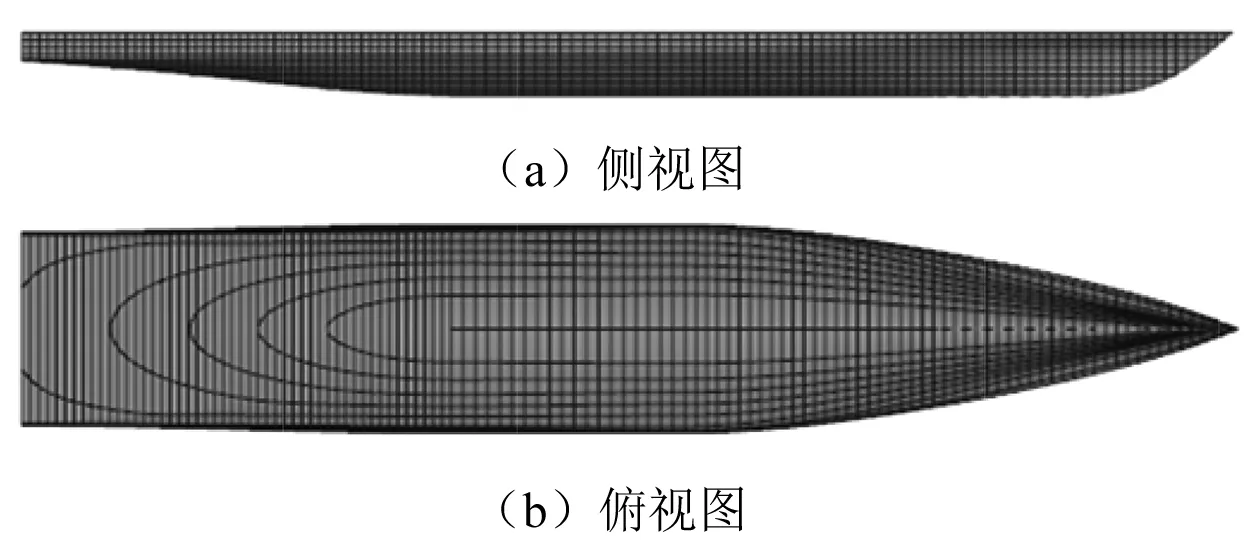
圖3 船體曲面面元網格

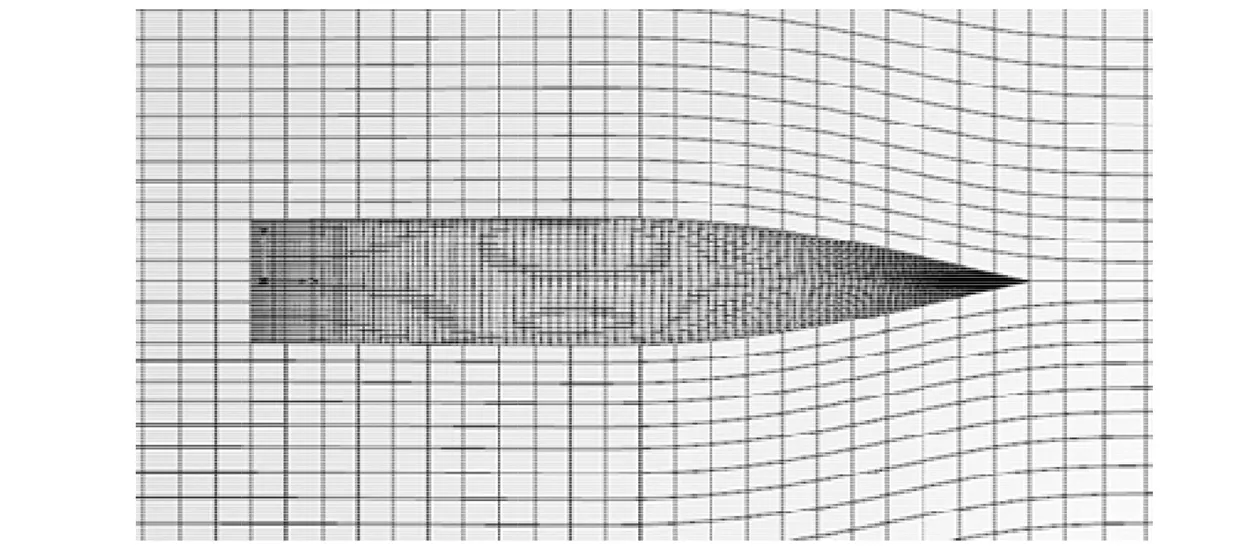
圖4 船體勢流計算網格與計算區域

2.2.3 數值分析

船體阻力系數CT的計算公式為

CT=CV+CW=CF+CPV+CW=

(1+h)CF+CW

(1)

式中：CV為黏性阻力系數；CW為采用壓力積分法進行計算得到的興波阻力系數；CF為摩擦阻力系數；CPV為黏壓阻力系數；h為形狀因子。

SHIPFLOW軟件對興波阻力進行計算的方法為橫切波法和壓力積分法，橫切波法對網格質量的敏感性相對較低。對初始模型進行阻力性能計算，分析計算結果發現：采用壓力積分法得到的初始模型興波阻力數值較船模高很多，而采用橫切波法則與船模接近。因此，確定后續計算采用橫切波法。船模與初始模型的15 kn(低速)、17 kn(中速)和19 kn(高速)(簡稱“多航速”)興波阻力數值如表2所示。由表2可知：船模與初始模型的興波阻力數值在多航速下誤差均在1%內。因此，初始模型可保證船型在阻力性能方面的擬合度和后續船型優化中的計算精度。

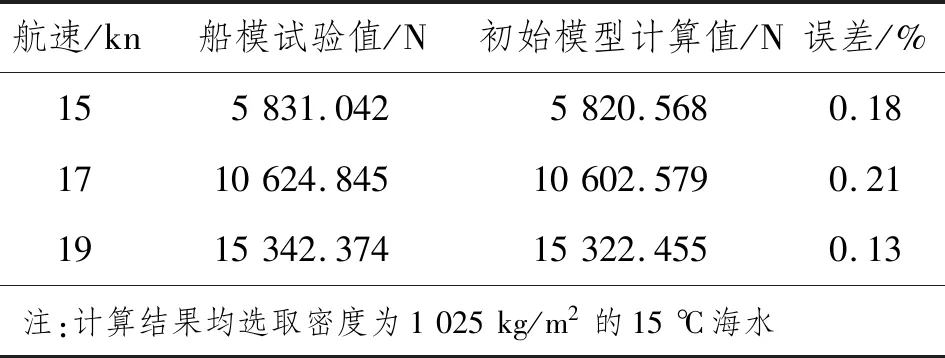
表2 多航速興波阻力數值

3 特征參數靈敏度分析

采用Sobol算法對選取的13個船體艏部特征參數進行靈敏度計算。在蒙特卡洛方法中，Sobol算法屬于擬蒙特卡洛方法，其優點在于是一種樣本分布均勻、穩定、覆蓋率很好的序列[7]。蒙特卡洛方法關鍵在于隨機數的生成，目前發展較快的是數學方法。Sobol算法基于半隨機的Sobol序列，其生成原理是基于1個以2為底數的不可約多項式生成多個方向數，對每個選定的優化變量由確定性計算生成偽隨機序列，設計方案以一種標準形式在整個空間域內進行傳播，使變量在設計空間內均勻分布。傳統的無約束優化算法在進行全局優化中具有一定的缺陷，而用Sobol算法在規定的研究空間內對最優解優化方向進行初步探索，所求的解不一定是最優解，但可以其作為研究對象，選擇其他優化算法進行進一步優化，從而節省優化時間。經靈敏度分析，得到靈敏特征參數及其最佳取值范圍，如表3所示。

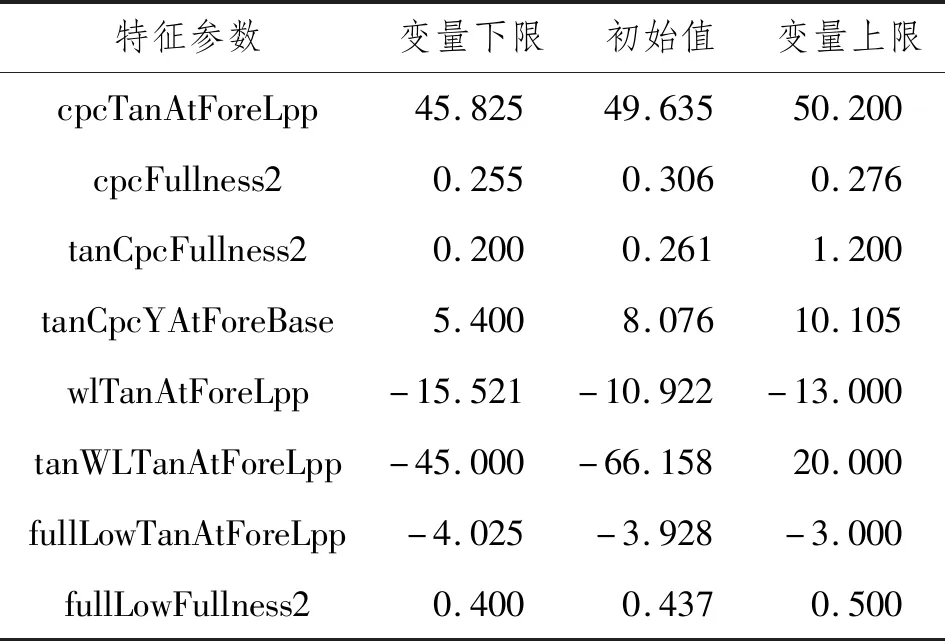
表3 靈敏特征參數及其最佳取值范圍

4 多航速船體型線優化

4.1 設計變量

將表3中的8個靈敏特征參數的變量上下限數值作為優化模型的設計變量。

4.2 約束條件

在模型優化過程中，將濕表面積和排水體積作為約束條件，使優化后的濕表面積和排水體積較優化前的誤差保證在±1%內，其約束公式為

(2)

(3)

式(2)和式(3)中：Sopti為優化模型濕表面積；Sorig為初始模型濕表面積；▽opti為優化模型排水體積；▽orig為初始模型排水體積。

4.3 優化目標

將15 ℃無風無浪海水中的多航速興波阻力作為優化目標并求其最小化。

4.4 優化結果數值分析

多航速優化模型的船體艏部特征參數數值如表4所示。多航速優化模型的約束條件和優化目標數值變化如表5所示。優化后的濕表面積和排水體積均滿足誤差絕對值在1%內，且興波阻力在多航速下均有所降低。

表4 多航速優化模型的船體艏部特征參數數值

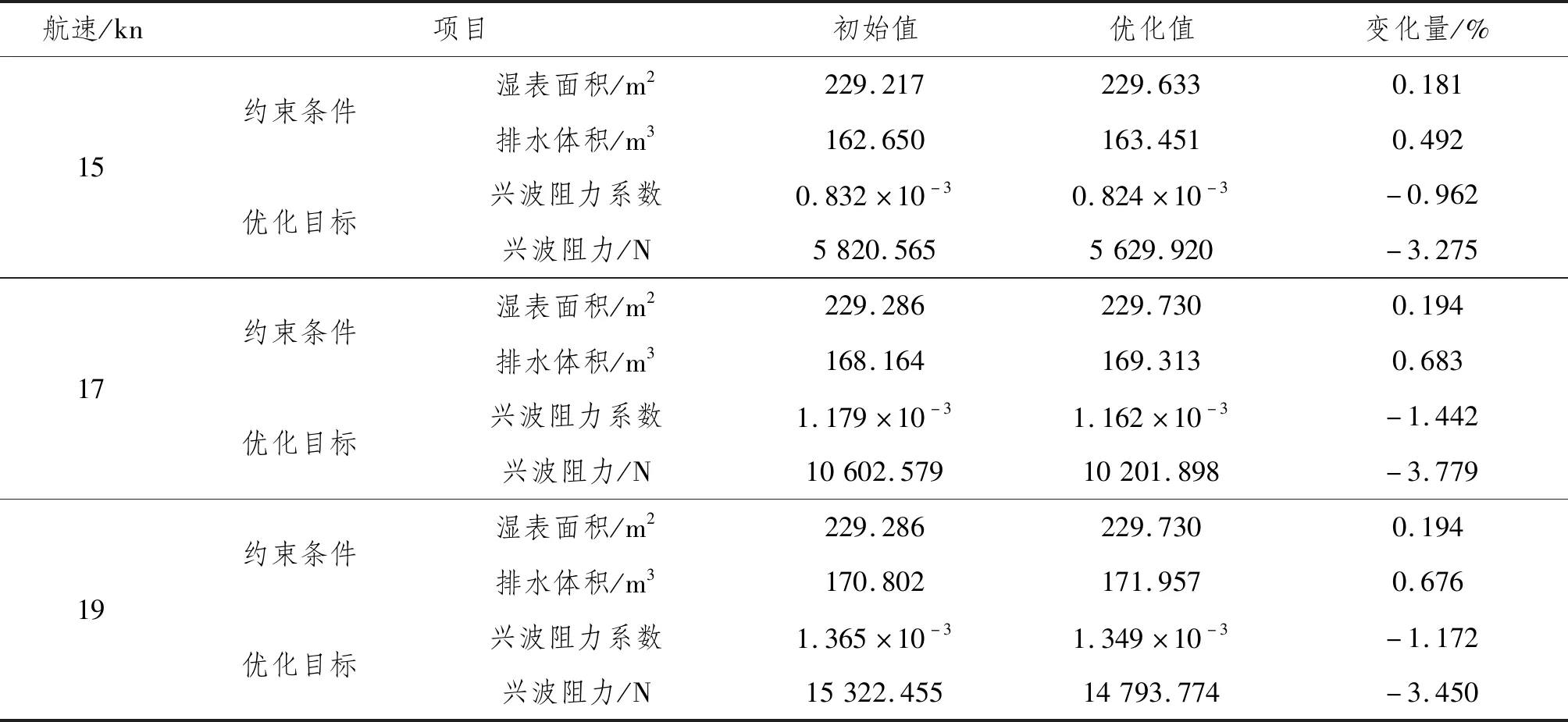
表5 多航速優化模型的約束條件和優化目標數值變化

4.5 優化結果圖形分析

優化模型的效果主要根據由波浪引起的自由液面波形圖及船體表面的壓力系數分布圖進行分析比較。

優化模型與初始模型的多航速自由液面波形圖對比如圖5所示。由圖5可知：在15 kn航速下，優化模型的最大波幅較初始模型有所降低，波數也有所降低，且幅值也較小；在17 kn和19 kn航速下，優化模型的波幅較初始模型無太大變化，波切圖波形走勢大體相同，但優化模型的波切圖波幅較初始模型有所減少。

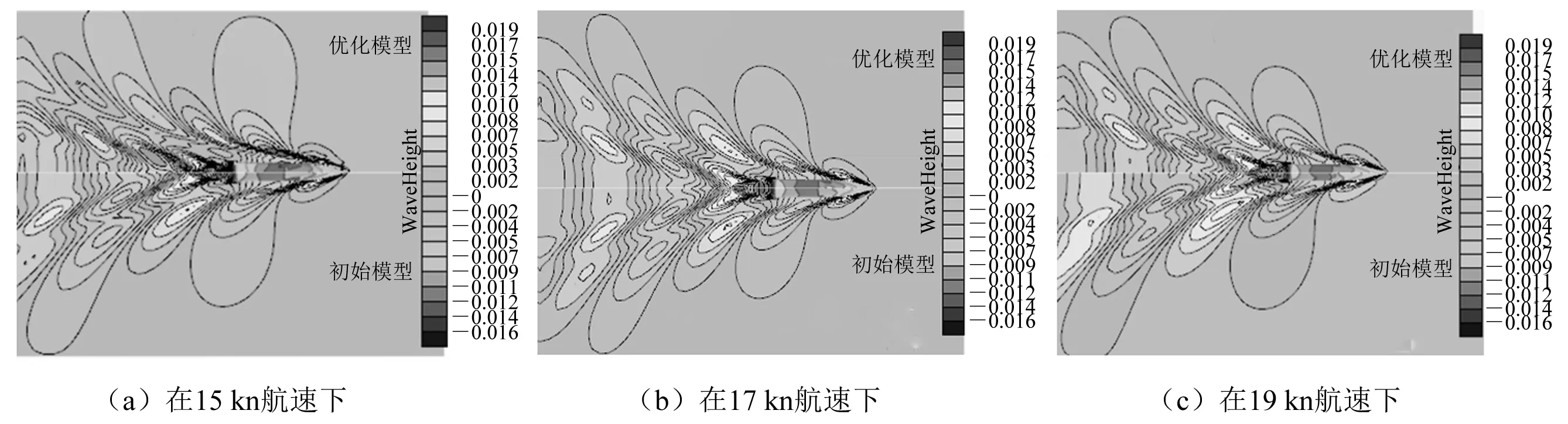
圖5 多航速自由液面波形圖對比

優化模型與初始模型的多航速船體表面壓力系數分布如圖6所示。由于只對船體艏部型線進行優化，因此在優化后，船體艉部表面壓力系數分布無大的變化。由圖6可知：優化模型的船體艏部壓力在多航速下較初始模型均明顯縮小，隨著壓力系數的減少，興波阻力也相應降低。在優化方案中，船體艏部壓力梯度在多航速下均變緩，且優化模型的船體前部壓力分布向船體后部移動，這樣優化后的興波分離降低，從而興波阻力也相應降低。

圖6 多航速船體表面壓力系數分布

對多航速優化模型與初始模型的型線進行對比，如圖7和圖8所示。由于只對船體艏部型線進行優化，因此船體艉部型線并無變化。由圖7和圖8可知：優化模型的船體艏部型線具有急速收縮的趨勢，水線面面積減少，從而導致興波阻力系數減少。

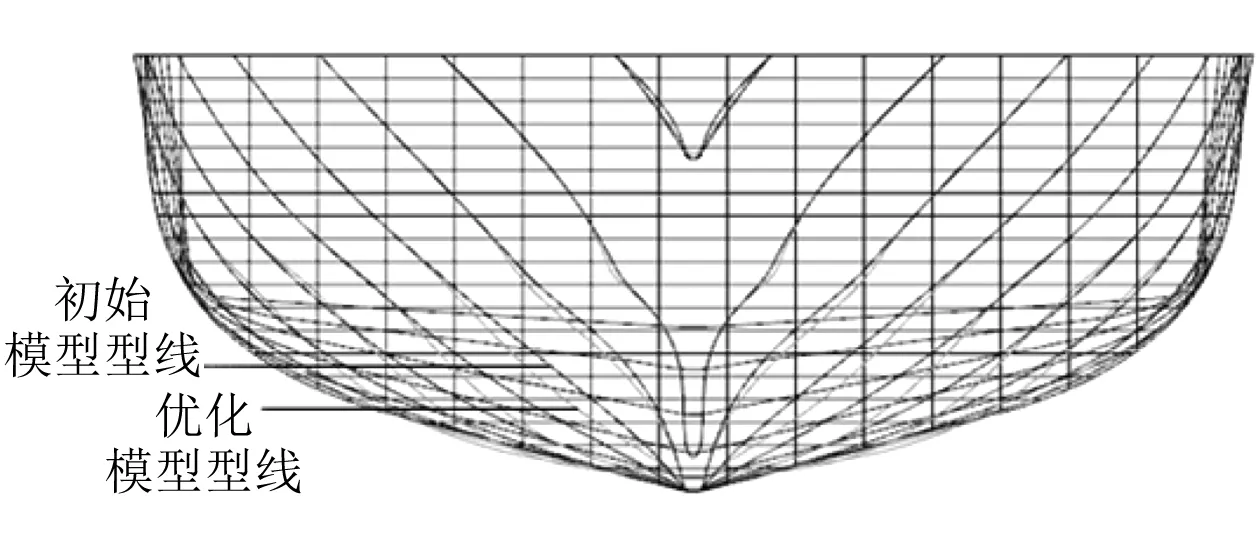
圖7 船體艏部橫剖線對比

圖8 船體艏部型線俯視圖對比

5 結 語

對多個優化方案進行分析，通過多次比較流場和阻力，優化模型在多航速下均具有良好的流場分布和較緩的壓力梯度分布，其興波阻力在多航速下較初始模型均明顯降低，且水面興波也較小。對于優化后的型線，除船體艏部具有1處存在稍不平緩現象外，其他各處均滿足曲線和曲面光順性的要求，由于在船舶建造過程中可進行人工光順，因此這種情況對興波阻力影響很小。綜合分析，可認為對某型高速客船的船體阻力性能優化是成功的。