二維彈道修正彈修正機構氣動特性研究

張德鍵,張 健,焦志剛,倪慶杰

(1.沈陽理工大學 裝備工程學院,遼寧 沈陽 110159;2.遼沈工業集團有限公司,遼寧 沈陽 110045)

目前,將常規炮彈智能化,以提高射擊精度、降低成本,是各軍事強國研究的重點,二維彈道修正彈就是在這個契機下誕生的[1]。

與常規榴彈相比,二維彈道修正彈在結構上加裝了二維修正機構,改變了二維修正彈丸外彈道運動過程中的力學特性,使二維彈道修正彈的運動更為復雜。COSTELLO[2]在1998年建立了雙旋二維修正彈的七自由度剛體彈道模型,隨后COSTELLO等[3]還給出了雙旋彈的陀螺穩定因子和動態穩定因子的表達式。WERNERT等[4-6]對155 mm的雙旋彈進行了風洞試驗,得到了氣動特性的變化規律,并建立了不同坐標系下雙旋彈的氣動模型,分析了不同坐標系下雙旋彈氣動參數的變化規律。JE等[7]用CFD仿真計算軟件對二維彈道修正彈進行氣動仿真,得到了不同馬赫數和舵偏角下二維修正彈的氣動特性。國內對二維彈道修正彈的研究起步相對較晚,近些年也取得了一定的研究成果。朱少雄等[8]分析了固定舵二維修正彈的氣動特性,將CFD仿真計算結果和風洞實驗結果進行對比,驗證了CFD仿真結果的可靠性。許巍等[9]對有舵彈丸和無舵彈丸進行了數值仿真,仿真結果表明,修正結構使彈丸的升力、阻力和滾轉力矩增大,從而影響了有舵彈丸的射程和散布。徐輝雯等[10]使用CFD對修正機構反旋與不旋進行了對比仿真,結果表明修正機構反旋會使阻力系數和升力系數下降,當彈丸攻角不為0時,彈丸存在側向力。張蛟龍[11]使用CFD軟件對鴨式布局雙旋彈進行了仿真計算,得到了當來流速度處于亞音速、跨音速和超音速時各項氣動參數的變化規律和流場分布規律。吳萍[12]設計了不同舵偏角鴨式布局二維修正彈的風洞實驗。觀察超音速下的紋理照片,發現彈丸頭部和圓弧部出現激波,影響修正能力,對模型進行改進后,采用CFD仿真計算改進后模型的升力、阻力、滾轉力矩和壓心系數的變化規律。

對彈丸氣動參數的研究是求解彈道方程、分析飛行穩定性的基礎。現有文獻中,對于二維彈道修正氣動特性的研究手段,多以風洞實驗和CFD仿真計算為主,在前期準備和實施過程中,需要耗費一定的時間。本文結合飛行器氣動特性工程計算方法建立二維彈道修正彈的氣動計算模型,引入升阻比,探究了二維彈道修正彈氣動特性與舵偏角和滾轉角的關系,為二維彈道修正彈結構設計和修正控制研究提供參考。

1 修正彈結構

二維彈道修正彈由修正機構和彈體組成,修正機構置于頭部,裝有4個固定舵偏角的舵片,兩兩成對,一對同向舵,一對差動舵,舵片為矩形對稱薄翼。彈體分為圓弧部(尖拱形)、定心部、圓柱部(忽略彈帶)和船尾部。彈體與修正機構通過滾動軸承連接,修正機構和彈體可以獨立旋轉,如圖1所示。

圖1 二維彈道修正彈結構

2 受力分析

無控時,修正機構舵片與彈體繞彈軸高速旋轉,舵片在舵機的作用下減旋且旋轉方向與彈體相反。有控時,修正機構固定不轉,滾轉角為φ,舵偏角為δ,全彈攻角為α,彈體仍保持旋轉。全彈的受力情況可視為兩部分,即修正機構舵片的受力和彈體的受力。

2.1 舵片間的干擾

修正機構采用十字型舵片組合體,如圖1所示,舵片兩兩垂直,水平方向為舵片1,同向舵,豎直方向為舵片2,差動舵。當氣流通過舵片時,舵片1的下洗流平行于舵片2的翼面,則舵片1與舵片2不產生相互影響。如式(1)所示,當舵片相互垂直時,上反角ψ為45°,此時Kψ=1.0,則進行十字型翼的受力時,可單獨分析一對舵片,再將兩對舵片疊加。

Kψ=2cos2ψ

(1)

式中:ψ為上反角[13]。

2.2 舵片受力分析

當攻角不為0時,氣流在攻角平面關于翼面不對稱,舵片迎風一側為高壓區,背風一側為低壓區,總的空氣動力在攻角平面內可以分解成垂直舵片面的法向力和平行于翼面與攻角平面交線的軸向力,再將法向力和軸向力向豎直方向和水平方向分解,得到舵片的升力和阻力,且升力向上為正,阻力向右為正。

一般二維彈道修正彈的兩對舵片,一對為同向,舵偏角方向相同,即兩側同為正或同為負。一對差動,舵偏角方向異向,即一側舵偏角為正,一側為負。下面將以舵片升力為例,對舵片的受力情況進行分析。

2.2.1 正舵偏角

當舵偏角為正時,舵片的有效攻角為α+δ,如圖2所示,法向力FN分解產生的升力Fy1,方向豎直向上。軸向力FA分解產生的升力Fy2,方向與Fy1相反。總升力大小Fw+=Fy1-Fy2,為方向豎直向上的正升力。

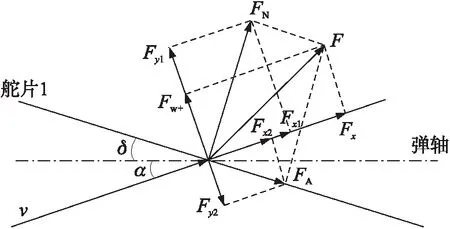
圖2 舵偏角為正時舵片的受力情況

根據空氣動力學線性理論,小擾動下機翼升力特性的計算方法,當舵偏角為正時,舵片升力的表達式為

Fw+=C′ypdSw(α+δ)

(2)

2.2.2 負舵偏角

當舵偏角為負時,舵片的有效攻角大小變為α-δ,如圖3所示。法向力FN和軸向力FA沿豎直方向分解產生的升力分別為Fy1和Fy2,二者方向相反，且合力方向豎直向上,為舵片提供正升力,升力大小Fw-=Fy1-Fy2,方向豎直向上。

圖3 舵偏角為負時舵片的受力情況

舵偏角為負時,舵片升力表達式為

Fw-=C′ypdSw(α-δ)

(3)

綜上分析,二維彈道修正彈同向舵為2個舵片的舵偏角同為正,其升力Fwt表達式為

Fwt=C′ypdSw(α+δ)

(4)

差動舵為2個舵片舵偏,舵偏角一個為正,一個為負,其升力Fwc表達式為

整理得:

Fwc=C′ypdSwα

(5)

2.2.3 滾轉角

滾轉角對舵片的受力情況如圖4所示。

圖4 滾轉角對舵片受力情況

如圖4所示,滾轉角對二維彈道修正彈的氣動特性的影響由兩部分組成,一部分為攻角與滾轉角的組合,另一部分為舵偏角與滾轉角的組合。

2.2.4 攻角與滾轉角組合

當舵偏角為0時,將舵片的升力分解為垂直翼面1的分量FN1和平行于翼面1的分量FN2,平行于翼面1的分量FN2垂直于翼面2。FN1=Fy,wcosφ,FN2=Fy,wsinφ。再將FN1和FN2沿豎直方向分解,得到翼1和翼2的升力為

Fy,w1=Fwtcos2φ,Fy,w2=Fwcsin2φ

(6)

則舵片升力表達式為

Fw=Fy,w1+Fy,w2=C′ypdSwαcos2φ+C′ypdSwαsin2φ

整理得:

Fw=C′y,wpdSwα

(7)

2.2.5 舵偏角與滾轉角組合

當攻角為0時,舵片1為同向舵,舵片2為差動舵,左右兩片差動舵產生的升力方向相反,數值相同,此時的升力僅由舵片1提供,舵片的升力表達式為

Fw=Fy,w1+Fy,w2=C′ypdSwδcosφ

(8)

綜上,當考慮舵偏角和滾轉角時,修正機構舵片升力系數為

Cy,w=C′y,w(α+δcosφ)

(9)

式中:a+δcosφ為舵片的合攻角。

2.3 彈體的受力分析

二維彈道修正彈彈體為旋成體,當攻角不為0時,其受力情況與普通榴彈相同,可參考文獻[14]。

3 氣動力計算

3.1 升力系數

彈翼之間存在相互干擾,致使二維彈道修正彈的升力系數不單純等于彈體升力系數與舵片升力系數之和,計算過程中需要考慮干擾的影響。當攻角不為0時,通過舵片的氣流在舵片上下表面形成了一個壓力差,使舵片產生升力。同時氣流通過舵片產生的自由渦系和附著渦系映射在彈體內部形成的鏡像渦系,使彈體產生了附加升力,這個附加升力就是舵片對彈體的干擾升力。

同樣,彈體對舵片也造成一定干擾,當氣流的垂直分量v∞sinα通過彈體時,在彈體兩側形成了上洗流,越靠近彈體,上洗流速度越大。在舵片和彈體結合位置,靠近彈體的上洗流作用在舵片上,對舵片的升力產生干擾。

綜上,可得二維彈道修正彈升力系數為

Cy=Cy,B+(Cy,wSw/Sm)

(10)

式中:Cy,B為彈體的升力系數,Cy,w為矩形舵片的升力系數,Sm為彈體橫截面積。

(11)

式中:Kα和Kδ為干擾因子,求解公式根據參考文獻[13]為

(12)

式中:舵片所在位置彈體直徑D與舵片展長l之比s=D/l。若設舵片展長為定值,可通過s的值分析舵片安裝位置對全彈氣動特性的影響。若舵片安裝位置為定值,則可通過s的值分析舵片展長對全彈氣動特性的影響。

3.2 阻力系數

全彈的阻力系數等于零升阻力系數與誘導阻力系數之和,加裝了修正機構后,其零升阻力可視為彈體零升阻力系數加上舵片的零升阻力系數,誘導阻力也可視為彈體誘導阻力系數加上舵片的誘導阻力系數。

Cx=Cx0B+(NCx0wSw/Sm)+CxiB+(CxiwSw/Sm)

(13)

式中:Cx0B為彈體的零升阻力系數;Cx0w為單獨舵片的零升阻力系數,等于舵片的摩阻與波阻之和;N為舵片數(對);CxiB和Cxiw分別為彈體的誘導阻力系數和單獨舵片的誘導阻力系數,舵片的誘導阻力系數包含彈體對舵片干擾產生的誘導阻力和舵片對彈體干擾產生的誘導阻力。

3.3 可靠性分析

以某型號固定翼二維彈道修正彈為算例,計算二維彈道修正彈氣動特性隨馬赫數的變化規律,與CFD仿真結果進行對比,驗證工程算法的可靠性。

全彈的結構參數:彈徑D=0.122 m,弦長b=0.046 2 m,舵片面積Sw=0.004 6 m2,彈體最大橫截面積Sm=0.011 7 m2,彈體橫截面積與側面積之比Sc=11.067 6,長徑比λ=5.97,彈頭部長徑比λn=3.2,圓柱部長徑比λc=2.06,彈尾部長徑比λt=1.0,彈尾收縮比st=0.5,根梢比η=1.0,展弦比λw=2.16,聲速為340 m/s,舵片數2對。

當攻角α=6°,舵偏角δ=4°,徑展比s=0.5,升力系數、阻力系數隨馬赫數的變化曲線如圖5所示。從圖5可以看出,隨著馬赫數的增大,升力系數呈先增大后減小再增大的變化趨勢,阻力系數呈先增大后減小的變化趨勢。將計算得到的升力系數曲線、阻力系數曲線與CFD仿真結果對比,升力系數的誤差為8.1%,阻力系數的相對誤差為9.5%,均小于10%,對于二維彈道修正彈氣動計算模型,滿足計算的可靠性。

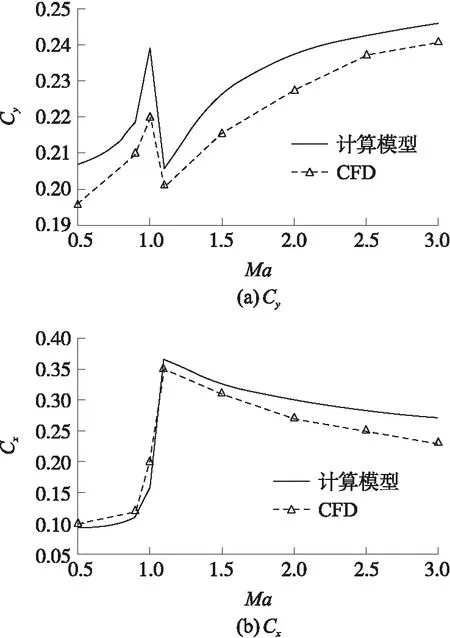
圖5 氣動力系數與馬赫數關系圖

分析產生誤差的原因:進行工程計算時設置的環境參數為定值,致使雷諾數等參數在計算時存在一定誤差;在工程算法中的需要查公式中的系數(如彈體的法向力系數)與彈丸結構的關系圖,查圖存在一定誤差;對于跨音速段的忽略也會造成一定的誤差。

4 舵偏角和滾轉角的影響

4.1 升阻比

為分析舵偏角和滾轉角對二維彈道修正彈氣動特性的影響,引入二維彈道修正彈升阻比ζK=Cy/Cx。

當二維彈道修正彈以最大的升阻比運動時,其氣動效率最好,氣動能力最佳[15]。

遺傳算法是一種模擬生物進化過程的計算模型,是一種搜索最優解的方法[16]。基于遺傳算法,對在舵偏角δ=0°且無控時的二維彈道修正彈的最大升阻比和最佳攻角進行尋優。設置種群數為1 000,進化代數為60,交叉概率為0.7,變異概率為0.01。求解結果,最大升阻比約為1.45,對應的最佳攻角約為13.7°,如圖6和圖7所示。

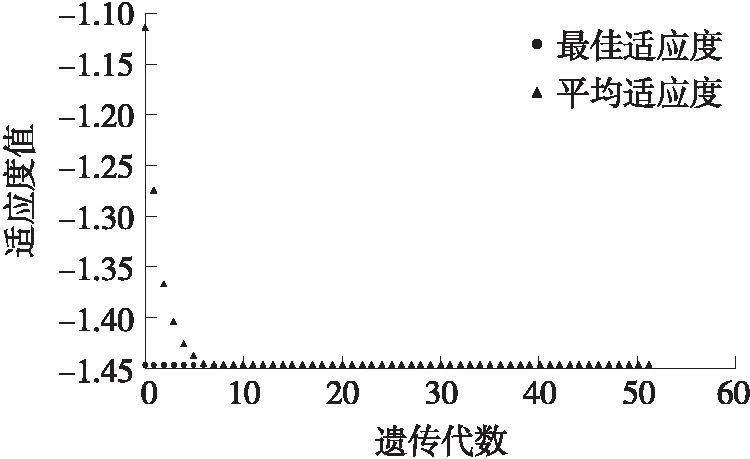
圖6 遺傳算法圖像

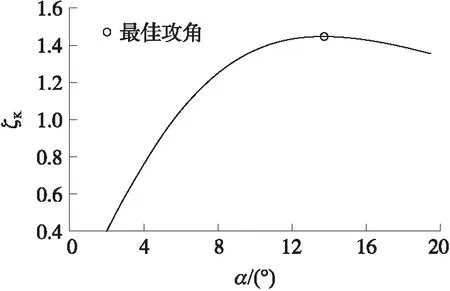
圖7 升阻比與攻角關系圖

4.2 舵偏和滾轉的影響

4.2.1 舵偏角的影響

圖8為修正機構舵片的舵偏角對二維彈道修正彈最大升阻比和最佳攻角的影響。由圖可知,通過對比遺傳算法的尋優結果,隨著修正機構舵偏角的增大,二維彈道修正彈的最大升阻比在減小,對應的最佳攻角也在減小。由此可知,當攻角較大時,較小的舵偏角可使二維彈道修正彈獲得更高的氣動效率和更好的氣動能力。當攻角較小時,較大的舵偏角可使二維彈道修正彈的氣動效率和氣動能力更好。當進行修正時,攻角越大,可控制舵偏角變小;若修正時攻角較小,可控制舵偏角變大。以保證修正時,彈丸有最好的氣動能力。

圖8 舵偏角與升阻比關系圖

4.2.2 滾轉角影響

采用遺傳算法對修正機構有控時(修正時)的滾轉角進行尋優,如圖9所示。

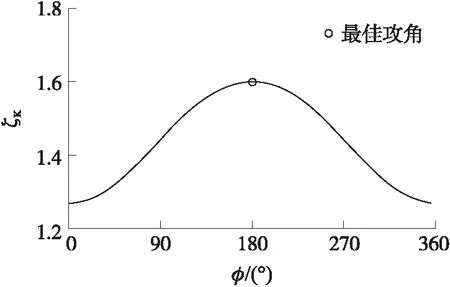
圖9 最佳滾轉角

圖9為攻角和舵偏角固定時,升阻比、滾轉角和最佳攻角關系圖。當滾轉角為180°時，全彈的升阻比最大。考慮滾轉角后,二維彈道修正彈全彈的升阻比隨攻角變化規律如圖10所示。

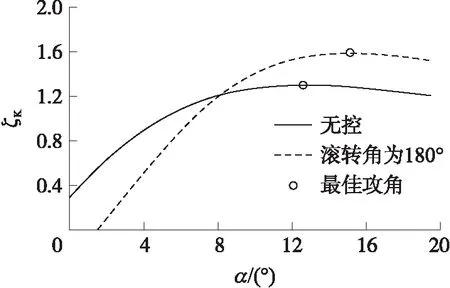
圖10 滾轉角與升阻比關系圖

從圖10可以看出,當攻角小于8°時,無控的二維彈道修正彈全彈具有更大的升阻比,當攻角大于8°時,滾轉角為180°時,二維彈道修正彈全彈具有更大的升阻比。最大升阻比對應的最佳攻角出現在攻角大于10°的區域,且其數值均大于無控時的數值。由此可見,當滾轉角處于180°時,二維彈道修正彈具有更好的氣動效率和氣動能力,此時對彈道的縱向修正效果更好。

5 結束語

本文通過對二維彈道修正彈進行受力分析,采用飛行器氣動特性工程計算方法,對二維彈道修正彈升力和阻力進行了仿真計算,分析了其力學特性的變化規律。計算結果與CFD仿真結果對比,相對誤差不大于10%。綜上說明本文使用的氣動計算模型能夠用于計算二維彈道修正彈的升力系數和阻力系數,分析結構參數對其氣動特性的影響,可為二維彈道修正彈氣動特性的研究和結構設計提供參考。

基于遺傳算法,分析了修正機構舵偏角和滾轉角對二維彈道修正彈氣動特性的影響。得出如下結論:全彈的最大升阻比和最佳攻角均隨修正機構舵偏角的增大而減小。當攻角較小時,舵偏角越大,全彈的氣動效率越好,氣動能力越好。若修正時,攻角較大,可控制舵片的舵偏角變小,攻角較小時修正,可控制舵偏角變大,使二維彈道修正彈在修正時氣動能力處于最佳狀態,以達到最佳的修正效果。在進行修正時,全彈的最大升阻比出現在滾轉角為180°時,且在攻角大于10°時,全彈的升阻比更大,氣動效率更高,彈道縱向修正能力更好。