諧振子的經典和量子統計分布

康琳惠，張 林

(陜西師范大學 物理學與信息技術學院，陜西 西安 710119)

經典統計是描述宏觀體系狀態的統計理論,而量子統計則是描述微觀系統統計性質的理論，兩種統計方法所遵循的統計原理本質上是相同的，即都是把系統的宏觀量作為相應微觀狀態的統計平均值.量子統計與經典統計的根本區別在于它們的動力學基礎不同，經典統計是以經典動力學為基礎，而量子統計則是建立在量子動力學的基礎之上，這就導致對微觀粒子運動的描述方式截然不同.諧振子模型作為在經典物理和量子物理中都非常重要的模型，是理解很多復雜體系行為的最基本單元.本文通過對諧振子系統的經典統計分布和量子統計分布的詳細研討，以Mathematica軟件為數學輔助手段，通過可視化的圖像，比較和歸納出經典統計與量子統計的區別和聯系.這一比較研究可以更加深刻地理解諧振子在宏觀和微觀尺度下不同的統計行為，從而加深對量子力學基本規律的理解和認知.

1 經典運動和統計分布

(1)

則運動方程可寫為

(2)

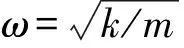
x(t)=Asin(ωt+φ)

(3)

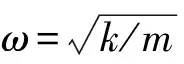
(4)

對于遵循經典運動的諧振子，我們可以由其在勢阱中位置的統計測量結果來獲得其運動的狀態.根據經典運動的解(3)，諧振子在平衡位置附近的運動被限制在-A到A之間.當我們大量測量振子的位置，會發現其位置在x到x+dx之間被測到的概率P(x)dx與振子在此區間停留的時間dt成正比

(5)

其中T是振子來回運動一次的周期，分子上的2表示振子來回過程中有兩次經過同一區域.值得一提的是，在周世勛先生編寫的《量子力學教程》(第二版)中的第33頁線性諧振子一節中[2]，給出的經典統計概率密度為

(6)

該式子沒有考慮到振子來回過程中有兩次經過同一區域，因此其概率密度也會加倍，所以分子上應該乘以2.該問題雖小，但由于這個2的存在，可以非常自然地得到經典的歸一化的概率分布.由式(5)有

(7)

其中v=dx/dt是振子在x到x+dx之間的運動速度.利用振子的運動方程：x(t)=Asin(ωt+φ)可以得到

(8)

將上式帶入P(x)得到歸一化的經典統計分布

(9)

這是一個在x=±A處有奇點的分布，運用Mathematica的積分函數Integrate[P(x),{x，-A，A}]可以非常方便地計算出P(x)的積分為1，即經典諧振子在區間[-A，A]上的經典分布自洽得滿足幾率之和為1.

2 量子運動和統計分布

如果把經典振子縮小到量子尺度，雖然振子所處的勢場不變，但振子的運動狀態將不能采用經典力學中的位置和速度(或動量)來描述，而其運動行為直接由波函數ψ(x)給出的統計性質來描述，波函數滿足定態薛定諤方程：

(10)

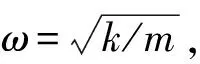
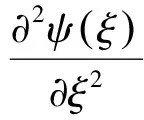
(11)

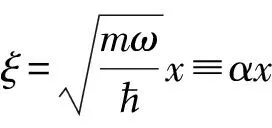
(12)

(13)

利用Mathematica程序對諧振子在經典平衡位置附近的分布進行圖像展示.如圖1給出了諧振子處于最低的幾個能態的波函數圖像，波函數的縱軸的位置是相應能級的位置.

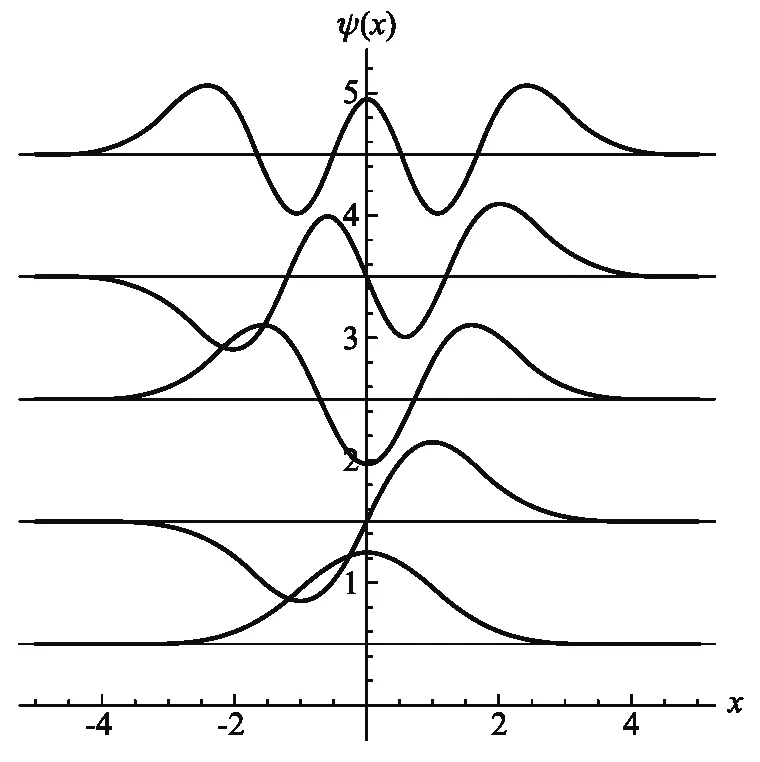
圖1 諧振子的波函數圖像分布(從下到上依次為n=0基態,n=1,2,3,4的波函數圖像)

由此可知，量子諧振子的波函數是坐標x(ξ≡αx)的函數，雖然它不能表示振子在某一時刻的位置坐標，但波函數絕對值的平方|ψn(ξ)|2與振子在空間某點出現的概率成正比，即它出現在某一位置的概率密度是可以確定的.一維諧振子的概率密度為

(14)

為此我們在Mathematica中做出其相應的概率密度分布如圖2.

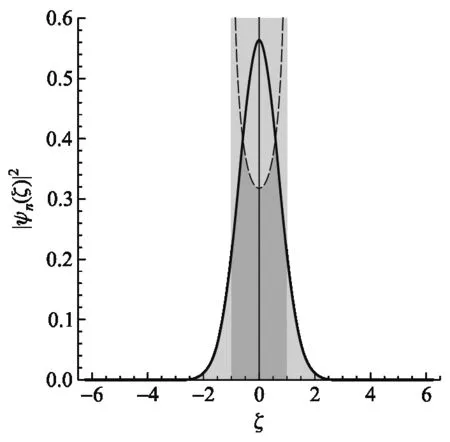
(a) n=0

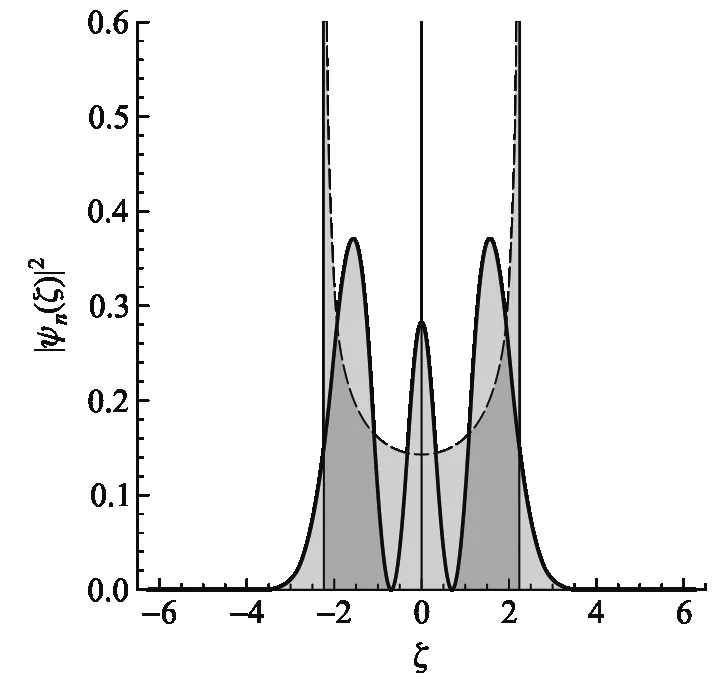
(b) n=2

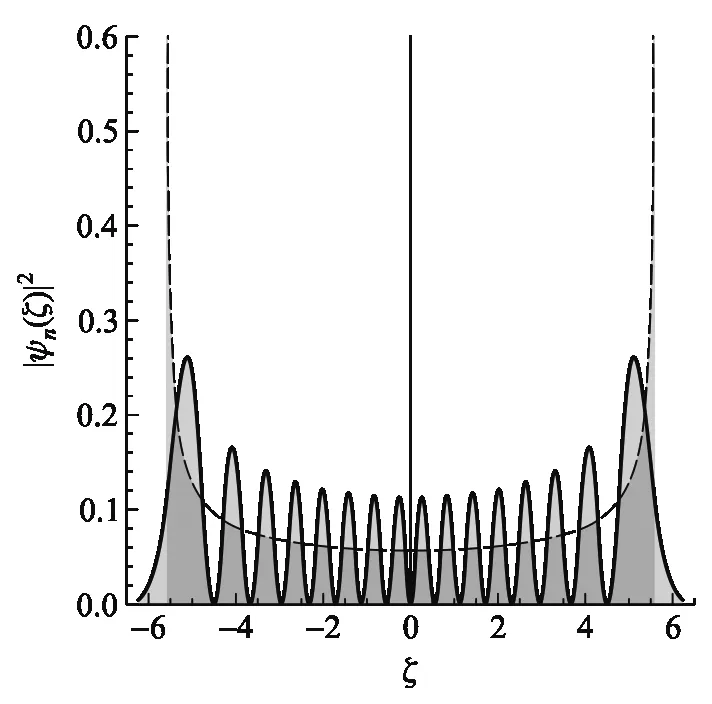
(c) n=15圖(實線)與對應經典概率分布(虛線)比較

從圖2中諧振子的經典(虛線)和量子(實線)概率密度分布可以看出：

1) 經典統計：對于經典動力學行為，在平衡位置ξ=0處，經典諧振子出現的概率最小，這是由于此時諧振子動能最大，振子在x=0處停留時間最短，測量到的概率也最小.而在兩邊最大值(振幅)處，振子的速度為零，停留時間較長，更容易測到振子，因而出現的概率最大.當然振子的能量越大其位置分布的范圍也越大.

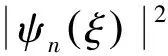
3 諧振子的經典和量子能量

經典諧振子的動能Ek和勢能Ep的表達式為

(15)

(16)

振子的總能量E

(17)

顯然在運動過程中，經典諧振子的能量是連續變化的且總能量保持不變.

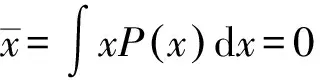
(18)

(19)

(20)

(21)

則有

(22)

(23)

可以得到

(24)

如果能量取成諧振子的量子能量，那么

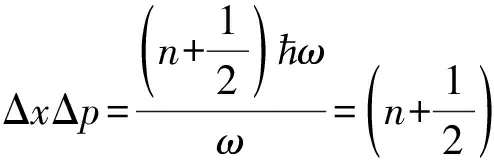
(25)

此統計結果與量子諧振子給出的統計結果也完全一致[1].

4 諧振子的相空間動力學描述

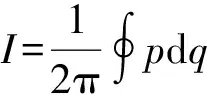
(26)

而量子力學中這個作用量是量子化的

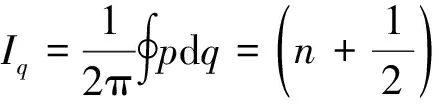
(27)

表明其能量是量子化的.

在諧振子的相空間的描述中，經典振子的動力學狀態是一個封閉的圓(標度后)，如圖3(a)所示.而對應振子的量子狀態在相空間的描述則比較復雜[5]，我們采用正定的Husimi函數[6]來描述振子相空間分布.對于任意數態|n〉，其相空間的Husimi分布函數為

(28)

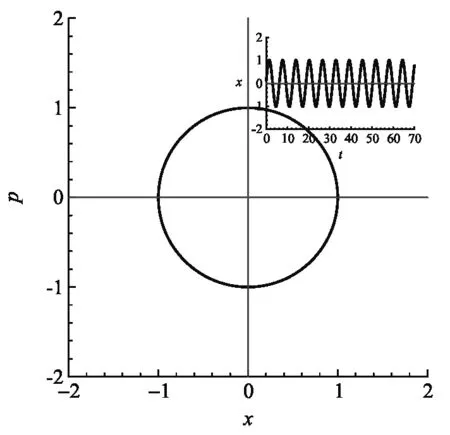
(a) 經典粒子的相軌道(右上角是隨時間的振動)

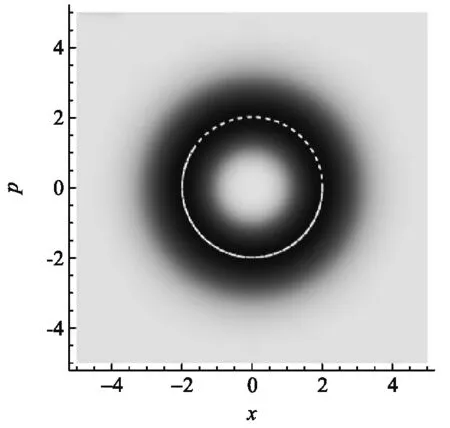
(b) n=1相空間分布(白色虛線對應能量的經典軌道)

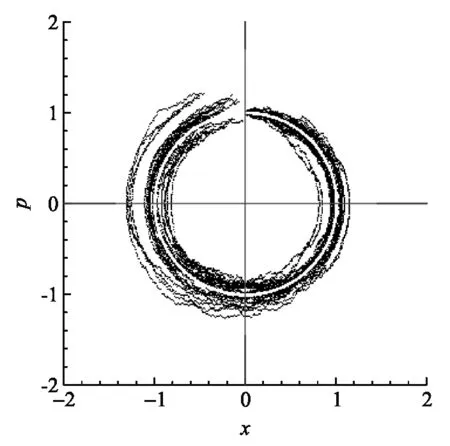
(c) 在經典軌道上加入隨機噪聲后的相空間演化軌道

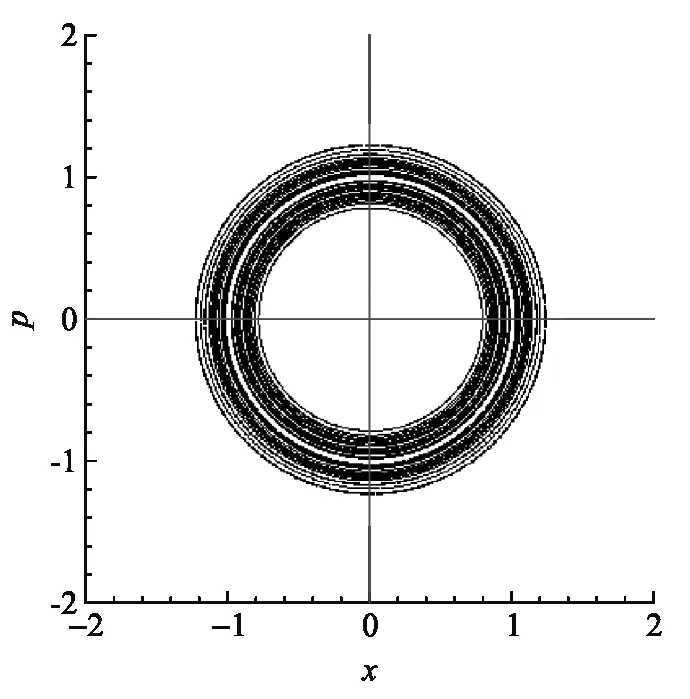
(d) 在經典軌道上(中間實線圓)加入初始動量為高斯分布的相空間軌道分布圖3 諧振子的相空間動力學描述

顯然對于相干態|α〉而言參數α的實部Re(α)和虛部Im(α)分別可以對應振子的位置和動量：

(29)

(30)

因此可得

(31)

(32)

數態|n〉的分布如圖3(b)所示為有寬度的環(虛線則為經典的軌道)，數態的量子軌道相空間統計分布體現了量子的漲落(環的寬度)，而經典相軌道(白色虛線)則只是量子平均的結果，顯然二者有本質的區別，因為量子的概率統計分布是無法用經典軌道加入隨機噪聲進行動力學統計來還原的.圖3(c)是在經典諧振子方程中引入高斯型白噪聲后多個隨機動力學軌道的相空間圖像，多個經典隨機軌道演化后的統計分布結果顯然和量子分布圖3(b)不同，所以微觀諧振子動力學行為不能簡單用加入隨機過程的經典動力學來進行模擬.同樣如圖3(d)所示，諧振子在相空間的量子統計分布也不能用初始動量為高斯分布的大量經典諧振子的相空間軌道來進行模擬，所以量子動力學給出的概率統計是全局動力學相干的，其空間概率分布是全空間相關聯的結果.當然當諧振子能量很大的時候諧振子經典相空間軌道和量子的環面會越來越接近，因為能量漲落(環的寬度)在大能量下基本可以忽略.

5 結束語

綜上所述，經過我們對宏觀和微觀諧振子的進一步研究發現，經典諧振子與量子諧振子的統計分布既有嚴重的分歧又有某些必然的聯系， 量子諧振子的行為只能在一定條件下趨近于經典諧振子而不可能完全等同[4].本次工作借助Mathematica軟件的數值計算和圖像展示功能，使比較抽象的諧振子問題變得更加形象和容易理解，通過比較諧振子系統的經典統計分布與量子統計分布為進一步理解相關物理規律奠定了基礎.