狄拉克δ-函數及有關應用

鄭神州， 康秀英

(1. 北京交通大學 理學院，北京 100044; 2. 北京師范大學 物理系， 北京 100875)

狄拉克δ-函數是一類“奇怪”的函數，有廣泛應用. 它按照通常古典的函數定義方式是無法做到，實際上它是非通常意義下的“函數”，更準確地稱為“廣義函數、Schwarz分布函數或泛函”，它是以英國理論物理學家狄拉克名字命名的，在數學和物理中有著獨特的地位[1,2]. 狄拉克 δ-函數可以用來描寫物理學中一切點量，如：點質量、點電荷、瞬時源等；數學上可以進行微分和積分變換，為處理數學物理問題帶來極大的方便. 尤其它在偏微分方程、數學物理方程、傅立葉分析和概率論等領域都離不開這個函數的應用[3-7]，有了狄拉克 δ-函數，傅立葉變換就不受絕對可積條件限制，通常稱為廣義傅立葉變換.

狄拉克δ-函數具有悠久的歷史, 這得從Kronecker δ-函數講起, Kronecker δ-函數非常簡單：

(1)

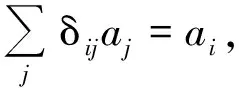
(2)

(簡記:(f*δ)(x)=f(x),f(x)δ(x)=f(0)δ(x))

(3)

δ(x-x0)=δ(x0-x)

(4)

從離散過渡到連續(xù)，自然地從求和過渡到積分；這看起來兩種δ-函數很雷同了. 所以狄拉克δ-函數就達到類似于Kronecker δ-函數的選擇器效果，對于δ-函數的選擇器作用是泊松先提出的，后來Cauchy利用它的選擇器性質研究了許多應用問題，進一步地傅里葉給出了其無窮級數表示，在此基礎上狄拉克對研究量子力學時發(fā)現了連續(xù)型的δ-函數重要作用. 物理上看，狄拉克δ-函數可以看成一些通常意義下函數列的逼近，但嚴格的數學理論表明：這不是通常意義下的極限(這是泛函意義下的極限，或稱“弱收斂”). 事實上，其真正嚴格意義下的定義方式是在Schwarz分布函數[2](廣義函數或泛函)基礎上才有的，這表明從此物理上廣泛實用的狄拉克 δ-函數可做數學嚴謹的推理了.

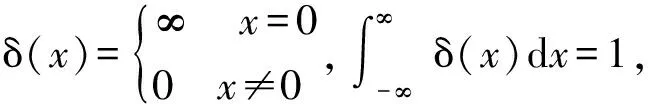
1 狄拉克δ-函數作為廣義函數定義

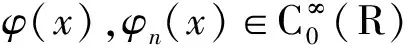
(5)

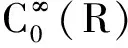
2) 狄拉克δ-函數定義[1,5]

〈δ,φ〉=φ(0), ?φ∈D(R)

(6)

它是廣義函數.事實上:

①δ(x)是線性的：對于任意的α、β∈R以及φ1(x)、φ2(x)∈D(R)，有

〈δ,αφ1+βφ2〉=αφ1(0)+βφ2(0)=α〈δ,φ1〉+β〈δ,φ2〉

(7)

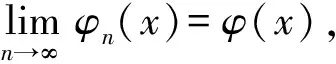
(8)

這里要強調的廣義函數收斂性一定要在試驗函數作用下收斂的，泛函分析中稱為弱收斂.

(9)

簡單的驗證：這是一個線性連續(xù)泛函.任一個局部可積函數按以上做法都有唯一的廣義函數與之對應，且可證明：不同的局部可積函數對應于不同的廣義函數，并保持線性運算不變；這樣可以將局部可積函數f等同于與其對應的廣義函數F.反之，狄拉克δ-函數不是通常函數，沒有局部可積函數與之對應[1,5].事實上，反證法：若存在這樣的局部可積函數f(x), 有

(10)

特別地取特殊的試驗函數為

(11)

則φ(nx)∈D(R),且

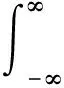
(12)

但另一方面

(13)

這是一個矛盾，所以狄拉克δ-函數沒有局部可積函數與之對應.

2 狄拉克δ-函數的逼近方式

上面定義的廣義函數有點抽象，下面我們從物理直觀上，用各種函數列逼近的方式來理解狄拉克δ-函數，這種逼近也不是通常意義下的極限，而是泛函意義下的逼近，是一種弱形式的極限[1,2,5].

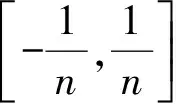
(14)

顯然Hn(t)∈Lloc(R)(積分值不超過1).

對任意φ(x)∈D(R)，有

(15)

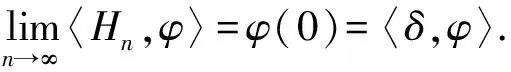
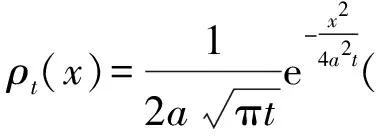
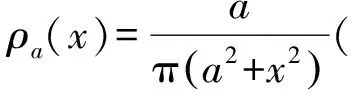
3 廣義導數(弱導數)和狄拉克δ-函數

先給出廣義導數定義:對一個廣義函數f∈D′(R),若存在f′ 使得

〈f′,φ〉=-〈f,φ′〉,?φ∈D(R)

(16)

則稱為廣義函數f有一階廣義導數，其廣義導數為f′(見文獻[1,2,5]).一般地，定義k-階廣義導數為；若有f(k)使得

〈f(k),φ〉=(-1)k〈f,φ(k)〉,?φ∈D(R)

(17)

稱f(k)為廣義函數f的k-階廣義導數，k=1,2,….注：通常意義下的導數一定是廣義導數，其本質就是分部積分公式；反之不對，從定義得知：廣義導數不是逐點定義的.例如：Heaviside函數

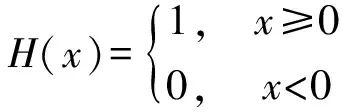
(18)

對于任意φ(x)∈D(R)，則有

(19)

所以狄拉克δ-函數可看作是Heaviside函數的廣義導數. 考慮函數|x|的第m階廣義導數(m為不小于1自然數)，有

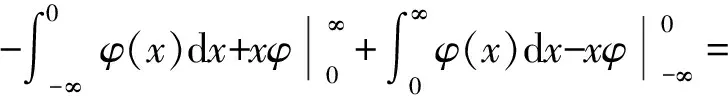
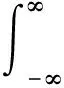
(20)

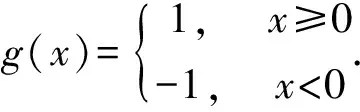
所以|x|′=2H(x)-1.一般地

|x|(m)=2δ(m-1),m≥2

(21)

4 狄拉克δ-函數性質和廣義傅里葉變換[1,3,5]

兩個已知函數f1(t)、f2(t)卷積定義：

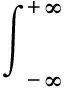
(22)

狄拉克δ(x)函數一些重要性質：

1) 卷積性質

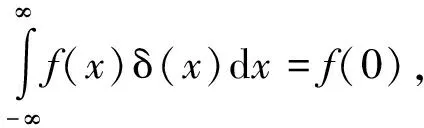
(23)

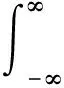
事實上，對于試驗函數φ(x)∈D(R)和f(x)的單零點an，由于f(an)=0,f′(an)≠0，在每個an存在鄰域都是一一對應，作局部的變量代換y=f(x)

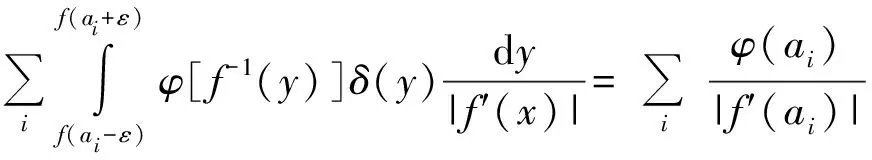
(24)

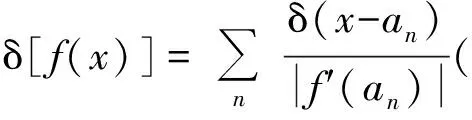
f(x)=(x2-a2)?δ(x2-a2)=

(25)

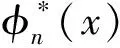
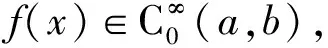
(26)

考慮{φn(x)}是正交基

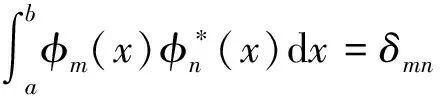
(27)

得證.

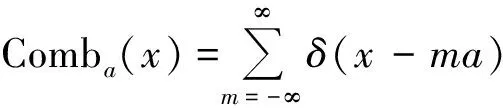
(28)

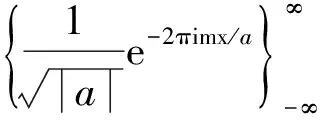
(29)

得證.

5) 三維狄拉克函數：δ(x,y,z)=δ(x)δ(y)δ(z)，即：

類似于一維的性質：

f(x0,y0,z0)， ?f(x,y,z)∈C(R3)

1)δ(x)函數的傅里葉變換為1,即:F[δ(x)]=1.

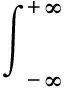
3) 又如求正弦函數f(t)=sinω0t的不是絕對可積的，但它的廣義傅里葉變換

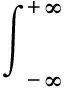
iπδ(ω+ω0)-δ(ω-ω0)

(30)

一般地，不滿足可積性條件函數的廣義傅里葉變換，其像函數通常與狄拉克δ-函數有關[8].

5 δ-函數在邊值問題中的應用

基本解和格林函數是由δ-函數來定義的.這里以拉普拉斯算子為例談論其在線性偏微分方程中邊值問題求解中的應用.

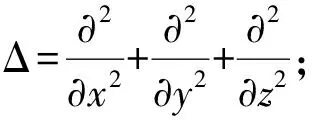
對于任意r∈Ω，有

(31)

其中n為?Ω上的外單位法向向量.