基于深度學習的冗余機械臂無碰運動規劃*

季曉明，文懷海

(1.江蘇安全技術職業學院電氣工程系，江蘇 徐州 221011；2.大連理工大學機械工程學院，遼寧 大連 116024)

0 引言

工業機器人是智能制造領域的重要構成單元，被廣泛應用于3C行業、汽車制造、食品包裝及航空航天等領域，在國民經濟與社會發展中起著重要作用。在機器人技術中，冗余機械臂無碰運動規劃問題一直是國內外的研究熱點[1-2]。該問題研究的是在避免碰觸到周圍環節障礙物的前提下，尋找從初始位形到目標位形的機械臂運動，其中避碰是核心。

機械臂的避碰研究一般分為全局避碰法與局部避碰法兩種[3]。前者需預先獲得機械臂周圍環境信息，再對機械臂進行離線規劃，常見的方法有A*搜索[4]、馬爾科夫決策法[5]、隨機樹形搜索法[6]等。這些方法雖能有效解決機械臂的避碰運動規劃，但也會帶來諸如關節位姿無法約束、算法極易陷入局部最優值、實時性較差等問題，故不易得到推廣。局部避碰法中含有碰撞檢測環節，可根據機械臂運動狀態與障礙物信息實時作出避碰決策，這也是目前最受學者青睞的方法。例如，曹博等采用改進人工勢場法分別在任務空間和關節空間內建立勢場引導7自由度機械臂的無碰運動，該算法的可行性在仿真和試驗下得到了驗證[7]。Shen H Y等采用主從任務轉化法實現了避碰運動與機械臂末端執行器運動的主從優先級轉化，降低了計算量和減少了運動奇異性出現的概率[8]。Chen Y J等用橢球模型近似描述障礙物與機械臂連桿，提出了基于虛擬力的避碰運動規劃方法[9]。然而，上述方法大都將障礙物簡化成一個質點或球形，忽略了機械臂連桿與障礙物原有的三維幾何信息，這樣會導致關節速度激變、末端執行器運動精度變差。

本文提出了一種基于深度學習的冗余機械臂避碰運動規劃方法，該方法的核心算法是基于天牛須搜索機制的循環神經網絡算法(Beetle Antennae Olfactory Recurrent Neural Network，簡稱BAORNN)，這屬于位置級而非速度級的運動規劃，即規劃過程中不要求末端執行器的初始位置處于參考軌跡上，可避免雅可比矩陣的計算、提高計算效率。另外，本算法中碰撞檢測策略選擇的是Gilbert Johnson Keerthi (簡稱GJK)算法，它能有效描述兩個多面體之間的距離[10]。最后，通過仿真算例對本文所提算法的可行性和有效性進行了驗證。

1 問題描述

考慮冗余機械臂跟蹤一條光滑曲線，其實質是將關節空間的運動軌跡投影到任務空間末端執行器的運動軌跡中，即可通過正向運動學來實現上述功能[11]：

x(t)=f(θ(t))

(1)

式中，t為時間，x(t)∈Rn為末端執行器位形，θ(t)∈Rm為關節角序列，m>n代表了機械臂構型上冗余。基于式(1)，可獲得冗余機械臂逆向運動學的描述形式為：

θ(t)=f-1(x(t))

(2)

在機械臂實際操作中應預先規劃好末端執行器的運動軌跡xr(t)。為了跟蹤該軌跡，關節角序列必須滿足[12]：

θ(t)=f-1(xr(t))

(3)

根據冗余機械臂的結構特性可知，式(3)存在關節角的多組解，即存在冗余性。為解決上述問題，需從關節空間中找出一組合適解，進而可將軌跡規劃問題轉化成如下函數優化問題：

(4)

這里的gtr(·)是軌跡規劃目標函數，其具體形式為：

(5)

在軌跡規劃問題中考慮避碰條件以保證冗余機械臂安全作業。選擇最大化末端執行器與障礙物之間的最小距離作為避障目標函數，并將其添加到式(4)中，有：

(6)

式中，O是障礙物頂點的笛卡爾坐標，gOI(·)是避障函數，即：

(7)

式中，β是超參數，di(O,θ(t))是第i根連桿到障礙物頂點的距離，由GJK算法計算獲得，具體形式如下所示：

(8)

式中，VA∈RnA×3和VB∈RnB×3分別為三維空間中不規則體A與B的頂點集合，nA和nB是最大頂點數。

由式(8)可知，GJK算法需要連桿和障礙物的幾何信息。定義連桿頂點函數為Mi(θ)∈Rni×3，即：

Mi(θ)=Ri(θ)Mi(0)+Ti(θ)

(9)

式中，ni是第i根連桿的頂點數，Ri(θ)和Ti(θ)分別為第i根連桿的轉動矩陣和移動矩陣。

2 BAORNN算法

冗余機械臂的避障控制包含三部分：軌跡規劃、避碰及關節角約束。綜合這些要求并將其轉換成函數優化問題，即：

(10)

式中，g(·)是總優化目標函數，其具體形式為：

g(O,xr(t),θ(t))=ω1gtr(xr(t),θ(t))+ω2gOI(O,θ(t))

(11)

式中，ω1和ω2為權重因子。

本文用BAORNN算法來求解上述優化問題。其中，BAO算法模擬的是天牛在未知環境下搜尋食物的過程，即天牛根據兩個觸須獲得的氣味大小來確定下一步的走向[13]。在這個過程中，天牛不會在任何方向上隨機移動，而是用嗅覺判明方向后，再做出下一步的計算決策，這可保證算法的多樣性。算法的數學機理為：

假設在第k次迭代時，機械臂的關節位置為θk，用標準正態分布函數b∈Rm模擬天牛左右兩個觸須接收到的氣味信息，即：

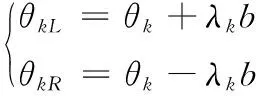
(12)

式中，λk是模擬兩觸須間距離的超參數，θkL和θkR分別為第k次迭代時左右關節角(對應兩個觸須氣味信息)，該位置應滿足如下約束：

ΩθkX=PΩ(θkX)

(13)

式中，X∈{L,R}。PΩ是關于集合Ω的投影函數，其數學描述為：

(14)

集合Ω的數學描述為：

Ω={θ∈Rm|θ-<θ(t)<θ+，di>dmin}

(15)

式中，di=di(O,θ(t))。

結合式(10)與式(13)，可得到用來評價當前關節位置的目標函數：

gkX=g(O,xr(t),ΩθkX)

(16)

進而，設計第k+1次迭代時關節預測位置為：

Ωθk + 1=PΩ[θk-δk(λk)sign(gkL-gkR)b]

(17)

式中，sign(gkL-gkR)b為符號函數，能保證天牛向著目標函數較小的觸角方向移動。δk(λk)為超參數，用來計算θ(k+1)X與θkX間的歐氏距離。上式可在預測的左右關節角中抉擇出較優值。

第k+1次迭代時預測關節角對應的目標函數為：

(18)

更新冗余機械臂的關節角與目標函數，即：

(19)

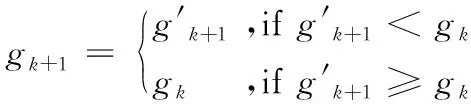
(20)

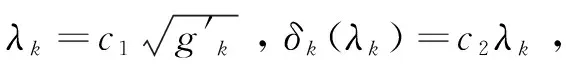
進而，將BAO算法添加進RNN中形成BAORNN算法，去解決冗余機械臂的避碰運動規劃問題，算法的流程如圖1所示。

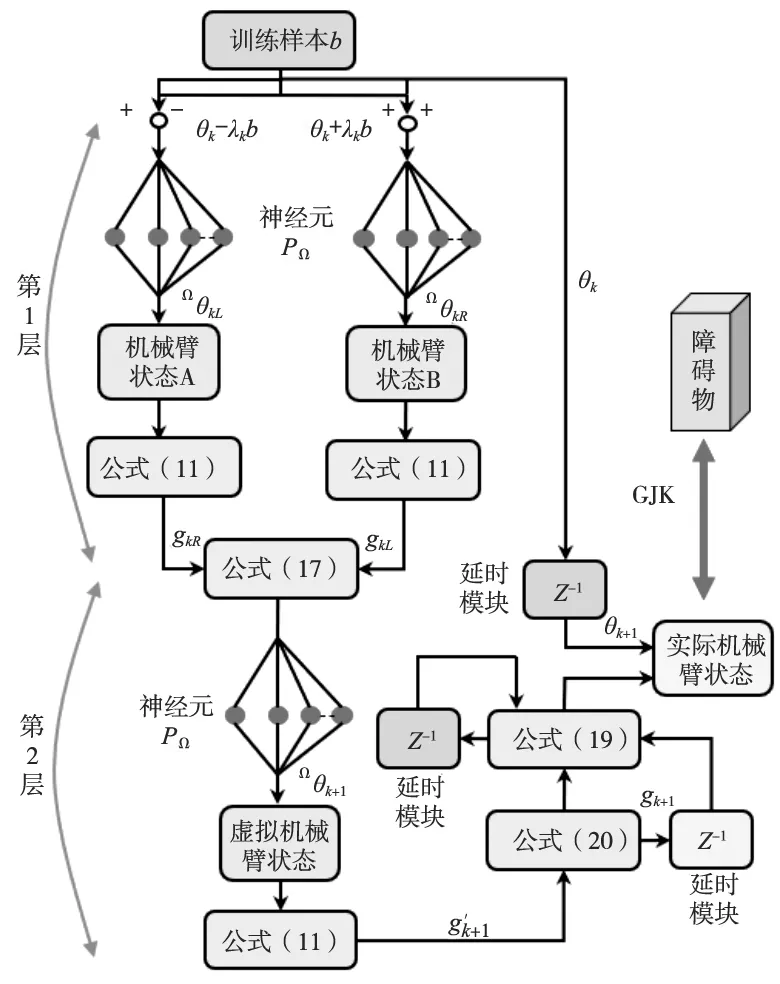
圖1 BAORNN算法流程圖

其中，RNN是一種常見的深度學習策略，其包括輸入層、隱藏層和輸出層，它將冗余機械臂關節角預測問題轉換為前后有依賴性的兩層時間序列問題，整個結構包括3m+6個神經元。在每個隱藏層中，用投影函數PΩ作為每個神經元的激活函數，并通過目標函數g(·)來判斷信號流向。根據上述分析可知BAORNN算法的計算復雜度為O(m)，即計算復雜度為關節數的線性函數，故可在普通計算機上高效率運算。

3 仿真算例

為驗證本文所提避障算法的合理性，選取文獻[14]提出的7-DOF冗余機械臂作為分析對象，該機械臂類似于肩腕關節偏置的仿人手臂，具有靈活性高、柔順性好的特點，如圖2所示。相應的DH參數也在表1中給出。另外，BOARNN算法的參數設置為：c1=0.6，c2=0.7，Tmax=500，ω1=0.7，ω2=0.3。仿真環境為Inter Core i7-4720 PC，MATALAB 2020a。

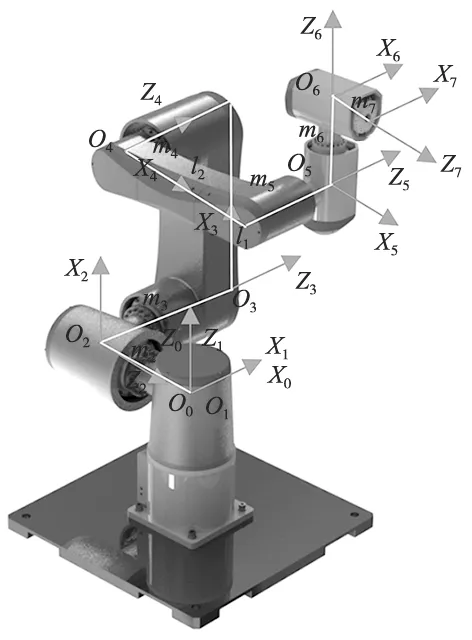
圖2 7-DOF冗余機械臂

表1 冗余機械臂的DH參數

仿真中，利用蒙特卡羅法[15]按照標準正態形式隨機生成機械臂的可達工作位形，并作為訓練樣本來訓練網絡。蒙特卡羅法的計算公式為：

θi=θimin+(θimax-θimin)·randn(0,1)

(21)

式中，randn(·)為呈正態分布的隨機函數。將生成的隨機關節角代入到正向運動學公式(1)，便可獲得冗余機械臂末端執行器的位形。這里的訓練樣本由1000個位形構成(如圖3所示)，取其中700作為訓練集，300作為測試集。

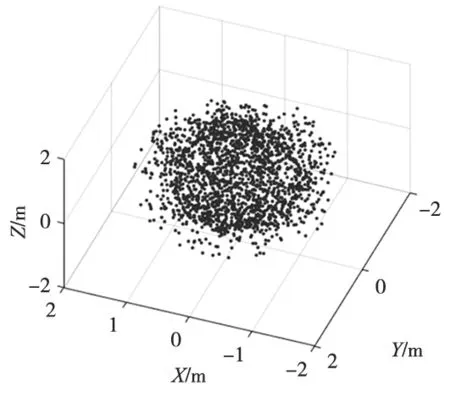
圖3 冗余機械臂的隨機位形

為了評價預測結果的優劣，選取單次預測的精度評估公式為：

(22)

式中，Ωθ是預測關節角，θ是參考關節角，δ為預測精度。對雙隱藏層的BAORNN算法，分別選取神經元數為15、21、27、33和39進行訓練，其預測精度如圖4所示。從圖中可以看出，隨著隱藏層神經元數目的增加，BAORNN算法的預測精度也隨之增加，當數目逾27后，預測精度卻開始下降，故選擇隱藏層的神經元數目為27。

圖4 預測精度

用訓練好的網絡預測測試集中的末端執行器位形，并計算其相對誤差，結果在圖5中給出。從圖中可以看出，在BAORNN算法的幫助下，測試集的相對預測誤差均小于5%，這說明了本文所提算法預測準確性較高。

圖5 BAORNN相對預測誤差

接著選取四面體的一個面作為待加工面，機械臂的末端執行器需沿著其三個頂點運動，此過程可模擬機器人焊接、噴涂等過程。假設工作環境中有一長方體障礙物，要求機械臂繞開障礙物并依次達到三個目標點位置。表2給出了待加工面和障礙物的坐標信息。為了比較BAORNN算法的性能，引入改進人工勢場法[7]進行比較，結果如表3所示。

表2 待加工面與障礙物的信息

從表3中可以看出，BAORNN算法的預測精度比改進人工勢場法平均高出10.89%、算法時間節約2.44 s。同時，基于BAORNN算法的冗余機械臂的無碰運動規劃效果如圖6所示。從圖中可以明顯看出機械臂的避碰過程和運動過程。圖7給出了7個關節角的響應，過程中沒有出現嚴重的關節突變，變化過程較為平滑、柔順。上述結果驗證了本文所提算法的可行性與優越性。

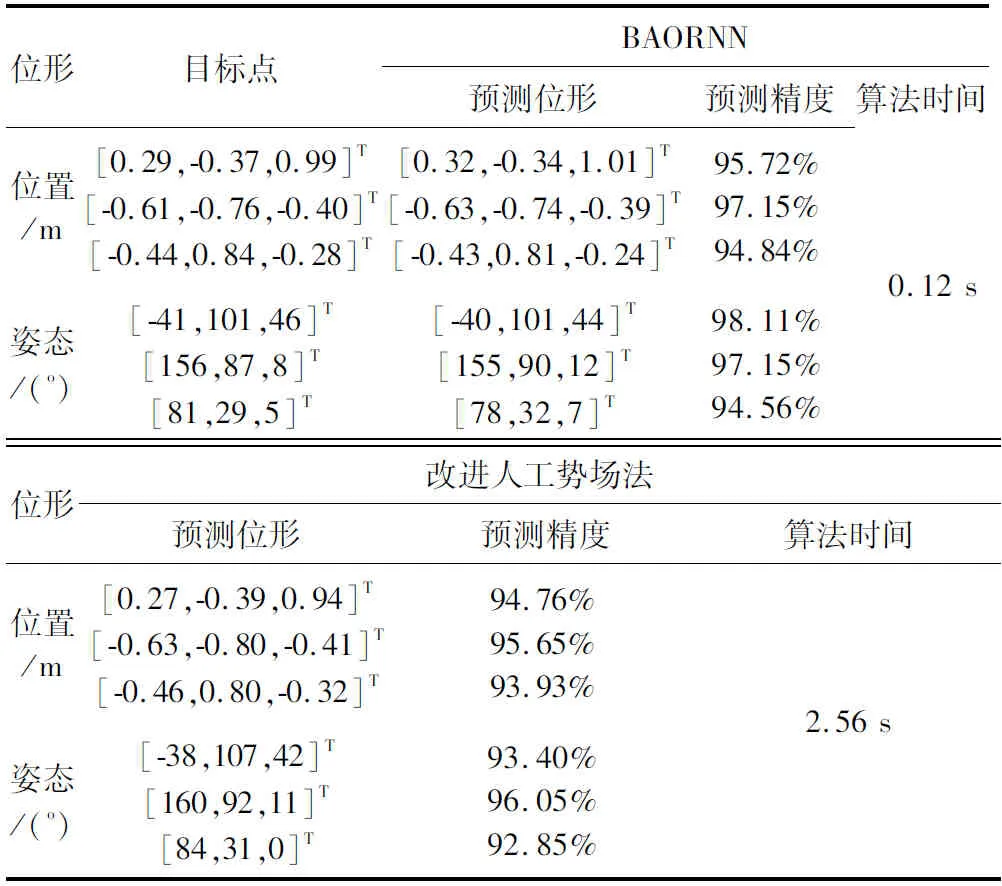
表3 兩種算法預測能力的對比

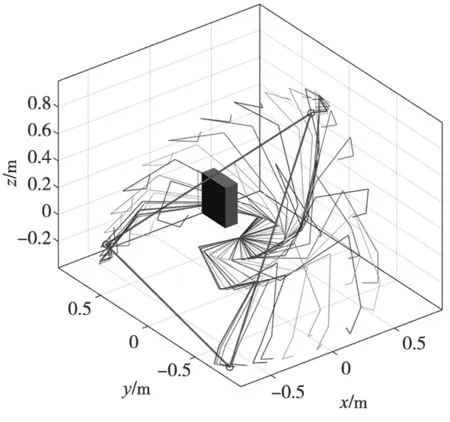
(a) 三維軌跡圖

(b) XY平面內的軌跡 圖6 冗余機械臂的運動規劃結果

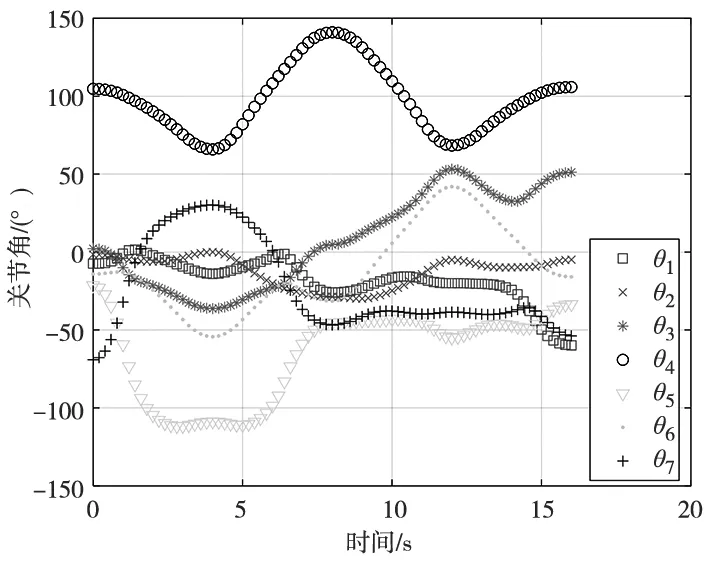
圖7 關節角的響應

4 結束語

本文針對冗余機械臂無碰運動規劃問題，提出使用BAORNN算法進行預測，主要結論如下：

(1)BAORNN算法的預測精度與神經元數目有關，仿真中最佳神經元數目為27，此時算法的預測精度最高。

(2)BAORNN算法的相對預測誤差小于5%，基本上能滿足本文冗余機械臂無碰運動規劃的需求。

(3)與改進人工勢場法相比，BAORNN算法的平均預測精度要高出10.89%，運算時間節約2.44 s。

(4)BAORNN算法具有較高的預測精度，能夠較好地解決冗余機械臂避碰運動規劃問題。