復合材料周期結構數學均勻化方法的一種新型單胞邊界條件

朱曉鵬， 陳 磊, 黃 俊

(1.安徽華電工程咨詢設計有限公司，合肥 230022； 2.北京航空航天大學 航空科學與工程學院，北京 100191；3.北京航空航天大學合肥創新研究院，合肥 230012)

1 引 言

復合材料具有比強度高和比剛度大等優點，廣泛應用于航天和航空工業領域。眾所周知，對于很多復合材料的宏觀解，如低階頻率和模態，可以使用等應變模型或等應力模型[1]以及其他均勻化方法[2]，但相對于宏觀應力分析，細觀分析要復雜很多。為了在計算精度和效率之間達到平衡，各種多尺度方法相繼提出，如數學均勻化方法MHM[3,4]、廣義有限單元方法GFEM[5,6]、多尺度有限單元方法MsFEM[7,8]、異類多尺度方法HMM[9,10]以及多尺度特征單元方法MEM[11,12]，在這些方法中，數學均勻化方法是具有代表性的方法，文獻[13-21]都作了詳細的闡述；文獻[22-28]討論了數學均勻化方法的攝動階次和使用的單元階次對計算精度的影響，在單胞上施加四邊固支邊界條件求解其影響函數控制方程，結果顯示對于一維結構是精確的，但對于二維結構計算精度不盡人意。

本文在文獻[22,24]的基礎上詳細研究了單胞影響函數控制方程在周期復合材料結構中的真實邊界條件，并以此為標準檢驗數值計算中施加的周期邊界條件計算精度，提出更為合理的二維結構單胞周期邊界條件。

2 數學均勻化方法矩陣列式

基于微觀周期性和單胞域的一致性假設，均勻化理論將異質邊界值問題分解為單胞(微觀)問題和結構問題(宏觀)，二維周期性復合材料結構的控制方程為橢圓型偏微分方程：

(1)

(2)

文獻[22,24]強調了二階攝動對數學均勻化方法計算精度的重要性，所以本文同樣考慮了二階攝動項的計算精度。

表1給出了一階和二階攝動位移的解耦形式以及影響函數的控制方程，其中EH為均勻化彈性模量，控制方程中的算子yj·和yn分別為散度和梯度。影響函數是單胞尺度(微觀尺度)y的函數，而均勻化位移及其各階導數只依賴于宏觀尺度x。從解耦形式和影響函數控制方程可以得到很多信息，詳見文獻[24]。

表1 攝動位移和影響函數控制方程Tab.1 Perturbed displacements and governing equations of influence functions

數學均勻化方法一般是通過有限元方法得以實現，所以需要將包含二階攝動項的數學均勻化方法的數學表達式通過加權殘量方法轉化為易于編程計算的矩陣列式，解耦的單胞影響函數控制方程矩陣列式為

(3)

(4，5)

(6)

宏觀均勻化位移控制方程為

KHu0=F0

(7)

(8)

式中D?Ω表示周期復合材料結構特定單胞區域，g為結構中單胞的數量。

求解結構宏觀位移導數和各階影響函數之后，宏觀結構單元節點的真實位移計算公式為

(9)

值得注意的是，對于周期復合材料結構，虛擬載荷和虛擬位移是以單胞為基本單位，且具有周期性，所以可以直接通過單胞結構計算其虛擬位移，然后復制到整個結構上，從而得到宏觀結構的虛擬載荷和虛擬位移，進而計算真實位移，此舉主要是減少計算量以提高計算效率，這也是數學均勻化方法在實際工程中得以廣泛應用的關鍵優勢所在。另一方面，為了求解方程(3)得到虛擬位移，需要施加周期性邊界條件，所以虛擬位移的計算精度很大程度上取決于周期邊界條件選擇的合理性，最理想的情況是施加的周期邊界條件能夠反映單胞在結構中的真實邊界變形情況，即可不因邊界條件的施加而引入誤差。

3 二維周期復合材料結構

為了更加詳細地研究周期復合材料單胞邊界條件問題，考慮一個四邊固支的矩陣平面周期復合材料結構，其結構尺寸為45 mm×45 mm，如圖1所示，每個單胞尺寸為9 mm×9 mm，內部包含一個矩陣夾雜，基體和夾雜的彈性模量分別為E1=2.97 GPa和E2=90.585 GPa，泊松比均為0.33。

圖1 二維周期復合材料及其單胞結構

3.1 單胞真實位移邊界條件

為了施加更為合理的單胞周期邊界條件，首先必須弄清求解影響函數控制方程(3)時，單胞在宏觀結構中真實的邊界情況，有效的方法是將整個宏觀結構作為一個大單胞來處理，即可避免額外施加單胞邊界條件，直接使用結構邊界條件求解虛擬位移(方法1)，這樣得到的虛擬位移在結構內部每個單胞邊界上的情況即為單胞真實位移邊界條件。

一階虛擬載荷F1由材料彈性參數矩陣決定，與單胞邊界條件無關，如方程(6)所示，F1矩陣的 3列 作為3個相互獨立的虛擬載荷作用在結構上，其矢量如圖2所示，分別對應F1矩陣的第1至第3列。可以看出，與F1相關的 3個 獨立虛擬載荷只有在基體和夾雜的交界線上具有非0的分段線性載荷。

圖2 宏觀結構F1矩陣矢量

(1) 宏觀結構內部單胞的真實邊界條件具有周期性。

(2) 宏觀結構內部單胞邊界的虛擬位移是非0的，圖3(c)表現尤為明顯。

圖3 宏觀結構真實邊界條件一階虛擬位1變形圖

(3) 宏觀結構單胞內部虛擬位移和邊界虛擬位移相差較大。

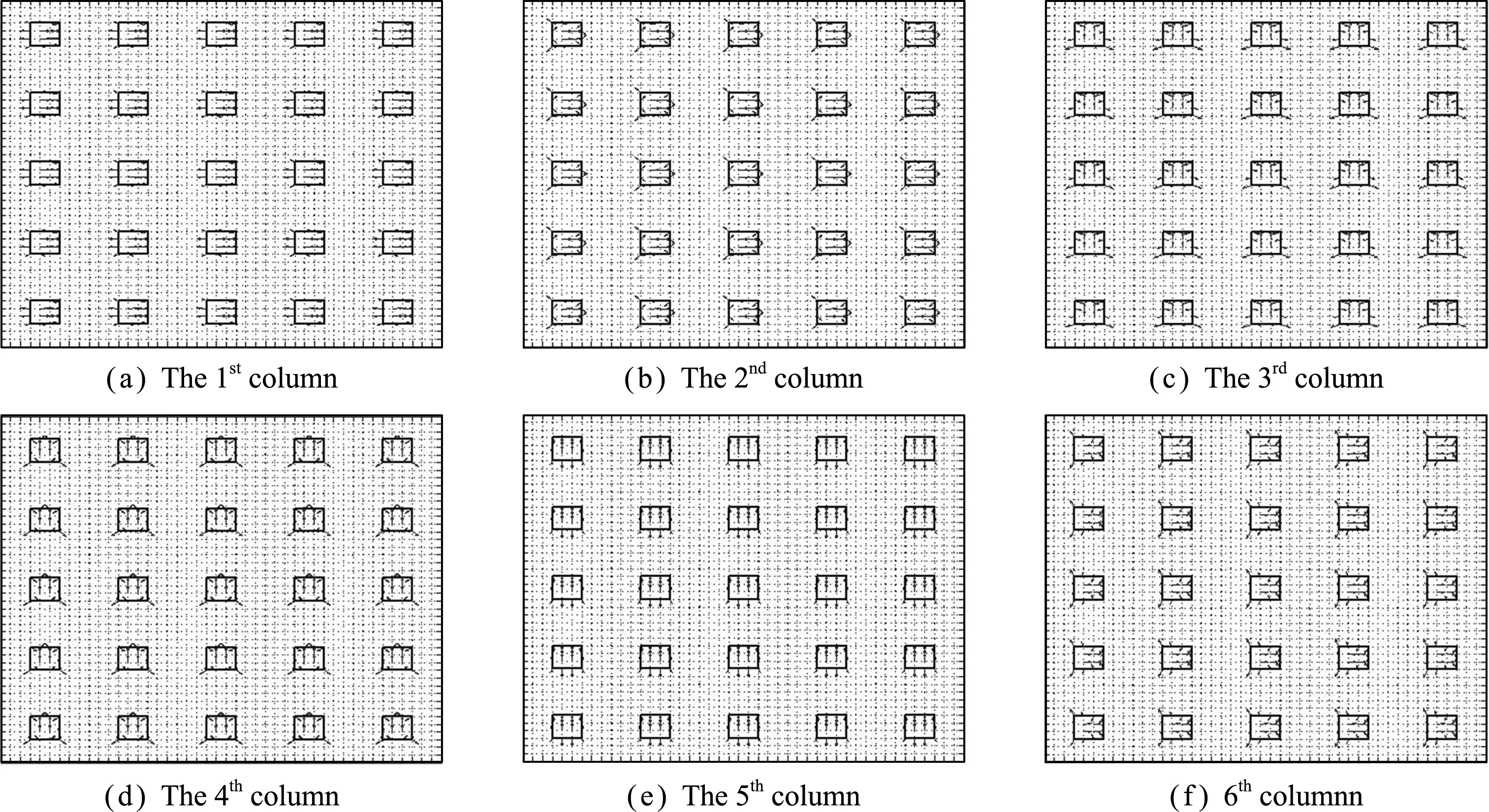
圖4 宏觀結構F2矩陣矢量

(1) 宏觀結構內部單胞的真實邊界條件仍然具有周期性。

(2) 宏觀結構內部單胞邊界二階虛擬位移相對一階虛擬位移變形更為明顯。

3.2 單胞影響函數控制方程邊界條件

3.2.1 四邊固支邊界條件

盡管四邊固支邊界條件廣泛應用于數學均勻化方法處理單胞邊界問題，但其對各階影響函數求解精度的影響尚未得到充分的研究。為了弄清該邊界條件的合理性，從結構中取出一個單胞施加四邊固支周期邊界條件分別計算一階和二階影響函數，然后利用單胞結構的周期性復制到整個結構中去，得到結構的虛擬變形圖(方法2)，與3.1節(方法1)得到的虛擬位移結構變形圖進行對比。

結構的一階和二階虛擬位移結構變形圖分別如圖6和圖7所示，分別與3.1節的圖3和圖5進行對比可以得到，

圖6 使用單胞四邊固支周期邊界條件的一階虛擬位移1結構變形圖

圖7 使用單胞四邊固支周期邊界條件的二階虛擬位移2結構變形圖

(1) 對于一階虛擬位移，方法1和方法2的虛擬位移結構變形圖的差別主要集中在單胞邊界上，但并不明顯。四邊固支邊界條件決定了單胞邊界上節點虛擬位移為0，而真實單胞邊界條件中邊界虛擬位移較小，所以使用四邊固支邊界條件求解一階虛擬位移是合理的。

(2) 對于二階虛擬位移，方法1和方法2得到的虛擬位移結構變形圖的差別十分明顯，同時表現在單胞邊界上的節點和單胞內部的節點，所以使用四邊固支邊界條件求解二階虛擬位移是不合理的，會造成很大的計算誤差。

3.2.2 超單胞周期邊界條件

從3.2.1節可以看出，盡管使用四邊固支周期邊界條件求解單胞虛擬位移較為方便，但對于二階虛擬位移的求解精度卻難以接受。實際上，單胞作為結構基本周期單元包含了所有的微觀信息，而且單胞的虛擬位移在邊界上取決于其在結構內部周圍單胞的相互作用，由此提出超單胞周期邊界條件(方法3)，即在9個單胞(3×3)組成的一個超單胞上施加四邊固支邊界條件，如圖8(a)所示，具體實現過程如下。

(1) 使用公式(3)計算超單胞的一階和二階虛擬位移。

(2) 將超單胞中9個單胞根據其在超單胞中的位置分為9種單胞，分別為A，B，C，D，E，F，G，H和I，如圖8(b)所示，每個單胞均有獨立的一階和二階虛擬位移。

(3) 將單胞E的一階和二階虛擬位移復制到結構內部的每一個單胞上，A，B，C，D，F，G，H和I共8個單胞的一階和二階虛擬位移根據其在超單胞中的位置分別對應復制到結構邊界上的單胞，如圖8(c)所示。

圖8 超單胞邊界條件實現過程

由超單胞周期邊界條件計算得到的一階和二階虛擬位移結構變形分別如圖9和圖10所示，將其分別與圖3和圖5對比，可以得到，

圖9 使用超單胞周期邊界條件得到的一階虛擬位移1結構變形

圖10 使用超單胞周期邊界條件得到的二階虛擬位移2結構變形

(1) 使用超單胞周期邊界條件得到的虛擬位移結構變形圖和真實邊界條件得到的虛擬位移結構變形圖差異較小。

(2) 超單胞周期邊界條件與真實單胞邊界條件相似，可以有效處理數學均勻化方法單胞問題。

3.3 虛擬勢能泛函

為了從數值上直觀反映超單胞周期邊界條件的計算精度，提出了與虛擬位移或虛擬載荷相對應的虛擬勢能泛函Π的概念，其計算公式如下，

Πk l p=Uk l p+Wk l p

(10)

表2和表3分別給出一階和二階虛擬勢能泛函的數值，其中ΠFEM表示使用真實單胞邊界條件(方法1)計算得到的虛擬勢能泛函，在此作為標準檢驗四邊固支周期邊界條件和超單胞周期邊界條件的計算精度，Π1為使用四邊固支周期邊界條件(方法2)計算得到的虛擬勢能泛函，Π2為使用超單胞周期邊界條件(方法3)計算得到的虛擬勢能泛函，從表2和表3的數值結果可以得到，

表2 對應一階虛擬位移的虛擬勢能泛函(107J)

表3 對應二階虛擬位移/載荷的虛擬勢能泛函(107J)

(1) 二階虛擬位移計算誤差要遠大于一階虛擬位移，即隨著虛擬位移階次的提高，無論施加何種單胞周期邊界條件，計算誤差都隨之增大。

(2) 使用四邊固支邊界條件計算一階虛擬位移的誤差較小，而二階虛擬位移計算誤差過大。

(3) 使用超單胞周期邊界計算虛擬位移的誤差大幅降低，說明超單胞周期邊界條件可以有效提高數學均勻化方法高階虛擬位移的計算精度。

3.4 數值算例分析

為了驗證上文分析結果的正確性，使用雙線性平面單元，在圖1結構中沿坐標x1方向施加面載荷f=0.1 MPa，每個單胞分為9×9個單元。為了方便研究單胞邊界條件對數學均勻化方法計算精度的影響，均勻化宏觀結構單元尺寸與單胞結構單元尺寸相同，均為1 mm×1 mm。

對四邊固支的二維周期復合材料結構分別使用上文中的三種邊界條件進行計算。

(1) 將整個結構作為一個大單胞進行處理，此時的單胞邊界條件與結構邊界條件相同，小參數ε=1，沒有引入周期邊界條件所帶來的誤差。

(2) 對單胞施加四邊固支周期邊界條件求解虛擬位移，值得注意的是，此時單胞單元的尺寸擴大5倍為5 mm×5 mm，小參數ε=1/5。

(3) 使用超單胞周期邊界條件求解虛擬位移，此時超單胞內的單元尺寸仍然擴大5倍為5 mm×5 mm，小參數ε=1/5。

使用這三種方法計算分別得到圖1中4條縱線A(穿過夾雜內部)、B(沿著單胞邊界)、C(沿著基體和夾雜交界線)和D(穿過基體)上的節點真實位移曲線，結果列入表4，其中FEM為有限元細網格計算結果，作為標準檢驗三種單胞邊界條件的計算精度，MsAEM1表示包含一階攝動項的節點真實位移，MsAEM2表示包含二階攝動項的節點真實位移，表5給出了勢能泛函的計算結果，計算公式為

(11)

由表4和表5的數值計算結果對比可以得到,

表4 沿著縱線A，B，C和D節點的真實位移曲線Tab.4 Actual displacements comparisons of line A,B,C and D

(1) 使用方法2，即四邊固支邊界條件得到的節點宏觀位移精度較差，根本原因在于四邊固支導致單胞邊界上的節點虛擬位移為0，即攝動位移為0，此時的節點宏觀位移就是均勻化位移；MsAEM2的精度在單胞內部較低，主要是由于二階虛擬位移計算精度較差。

(續表)

(2) 使用方法1和方法3得到的包含二階攝動位移的節點宏觀位移計算精度較高，也驗證了文獻[22]二階攝動項必要性的結論。

(3) 方法1和方法3的計算結果十分相近，說明超單胞周期邊界條件很好地反映了單胞在結構中的真實邊界條件，可以有效地處理數學均勻化方法中的單胞邊界問題。

4 結論

詳細研究了數學均勻化方法單胞邊界條件計算精度的問題，將影響函數作為虛擬位移得到了周期結構內單胞的真實邊界條件，并提出了與之相應的虛擬載荷和虛擬勢能泛函的概念，得到結論如下。

(1) 固支周期邊界條件不適合作為二維結構單胞邊界條件。

(2) 提出超單胞周期邊界條件，大幅提高了二維周期復合材料結構數學均勻化方法的計算精度。

(3) 使用虛擬勢能泛函驗證了不同邊界條件和攝動階次對結構宏觀位移計算精度的影響，進一步確定了二階攝動項對數學均勻化方法計算精度的必要性。