無網(wǎng)格穩(wěn)定配點(diǎn)法及其在彈性力學(xué)中的應(yīng)用

王莉華， 劉義嘉， 鐘 偉， 錢志浩

(同濟(jì)大學(xué) 航空航天與力學(xué)學(xué)院，上海 200092)

1 引 言

無網(wǎng)格法[1-4]在數(shù)據(jù)輸入時不需要提供單元連接信息，即節(jié)點(diǎn)之間不受網(wǎng)格結(jié)構(gòu)限制，很大程度上節(jié)省了建模的時間和成本，而且可以在計算中根據(jù)需要改變節(jié)點(diǎn)的位置而不存在網(wǎng)格畸變問題，因此在大變形、高速碰撞、斷裂破壞、金屬成型以及微觀粒子運(yùn)動等復(fù)雜問題分析中具有明顯優(yōu)勢，常應(yīng)用到一些傳統(tǒng)的數(shù)值計算方法(如有限元法和邊界元法等)無法很好解決和尚未觸及的領(lǐng)域。常用的無網(wǎng)格法主要分為基于伽遼金法的弱形式和基于配點(diǎn)法的強(qiáng)形式兩類。伽遼金型無網(wǎng)格法主要包括擴(kuò)散單元法DEM[5]、無網(wǎng)格伽遼金法EFG[6]、重構(gòu)核粒子法RKPM[7]、hp云團(tuán)法[8]、單位分解法PUM[9]、無網(wǎng)格局部彼得洛夫-伽遼金法MLPG[10]、徑向點(diǎn)插值法RPIM[11]和光滑粒子伽遼金法SPG[12]等。配點(diǎn)型無網(wǎng)格法主要包括徑向基函數(shù)配點(diǎn)法RBCM[3-15]、分區(qū)徑向基函數(shù)配點(diǎn)法SRBCM[6-18]、局部徑向基函數(shù)配點(diǎn)法[19]、徑向點(diǎn)插值配點(diǎn)法RPICM[20]、重構(gòu)核近似配點(diǎn)法RKCM[21,22]、有限點(diǎn)法FPM[23]和hp無網(wǎng)格云團(tuán)法[24]等。

伽遼金型無網(wǎng)格法具有精度高和穩(wěn)定性好的優(yōu)點(diǎn)，但是由于無網(wǎng)格形函數(shù)通常是有理式，且形函數(shù)影響域與背景積分網(wǎng)格通常不重合，所以伽遼金型無網(wǎng)格法通常難以實現(xiàn)準(zhǔn)確的數(shù)值積分。雖然穩(wěn)定節(jié)點(diǎn)積分SCNI[25-27]等技術(shù)能夠提高積分精度，但是積分過程較為復(fù)雜，尤其是構(gòu)建高階穩(wěn)定節(jié)點(diǎn)積分顯著增加了問題求解的復(fù)雜度。因此伽遼金型無網(wǎng)格法的效率較低，進(jìn)行大規(guī)模計算非常耗時。配點(diǎn)型無網(wǎng)格法構(gòu)建模式簡單，不需要積分，所以效率非常高，而且結(jié)合一些特定的形函數(shù)還可以獲得超收斂率[15]。然而，由于采用單個配點(diǎn)方程代表附近求解區(qū)域的信息而不對整個區(qū)域積分，其在求解一些復(fù)雜問題時精度和穩(wěn)定性往往較差[3]。

本文針對伽遼金型和配點(diǎn)型無網(wǎng)格法的缺點(diǎn)，介紹一種改進(jìn)的配點(diǎn)法,即無網(wǎng)格穩(wěn)定配點(diǎn)法，該方法采用重構(gòu)核函數(shù)作為近似函數(shù)，構(gòu)建規(guī)則子域進(jìn)行準(zhǔn)確積分。該方法在構(gòu)造近似場函數(shù)和數(shù)值積分中不需要背景網(wǎng)格，是一種真正的無網(wǎng)格法。其僅在規(guī)則子域積分，而不是像伽遼金法一樣在整個求解區(qū)域積分，既保留了配點(diǎn)法效率高的特點(diǎn)，又具備伽遼金型無網(wǎng)格法精度高和穩(wěn)定性好的特點(diǎn)，而且還兼具有限體積法滿足局域離散方程守恒的特點(diǎn)。與伽遼金型無網(wǎng)格法相比，無網(wǎng)格穩(wěn)定配點(diǎn)法的計算效率更高；與配點(diǎn)型無網(wǎng)格法相比，本文方法穩(wěn)定性好且精度高。該方法兼具效率高、精度高、穩(wěn)定性好和局域離散方程守恒的特點(diǎn)，可以應(yīng)用于固體力學(xué)問題的求解，未來可將其進(jìn)一步應(yīng)用于流體力學(xué)和流固耦合問題分析。

2 重構(gòu)核近似

重構(gòu)核近似和移動最小二乘是無網(wǎng)格法中最常用的兩類形函數(shù)，當(dāng)采用多項式作為基函數(shù)時，移動最小二乘近似和重構(gòu)核近似在本質(zhì)上是等價的。在重構(gòu)核近似中，假定近似函數(shù)可以表示為

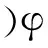
(1)

式中c(x)是需要確定的未知矢量，HT(x-xI)是一組基矢量，其表達(dá)式如下，

HT(x-xI)=[1,x-xI,y-yI,…，

(x-xI)m(y-yI)n,…,

(y-yI)p]

(m+n≤p)(2)

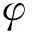
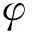
(3)

式中rx=|x-xI|/θx,ry=|y-yI|/θy,θx和θy分別表示x和y方向影響域的大小，通常可取θx=θy。核函數(shù)可取如下三次B樣條函數(shù)，

(4)

式中r=‖x-xI‖/θ。為了保證數(shù)值求解的精度和穩(wěn)定性，形函數(shù)需滿足如下的p階一致性條件，

(m+n≤p)(5)

式中N為影響域內(nèi)離散點(diǎn)的個數(shù)。式(5)可改寫為

(6)

將式(1)代入式(6)可得未知矢量為

c(x)=M-1(x)H(0)

(7)

式中M(x)稱作矩量矩陣，表示為

(8)

將式(7)代回式(1)可得重構(gòu)核近似的表達(dá)式為

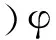
(9)

其一階和二階導(dǎo)數(shù)為

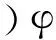
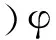
(α=x,y)(10)

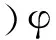
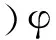
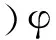
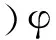
(α=x,y;β=x,y)(11)

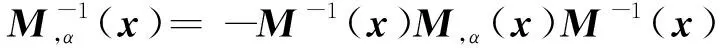
(12)

(13)

3 重構(gòu)核配點(diǎn)法

在重構(gòu)核配點(diǎn)法RKCM(Reproducing Kernel Collocation Method)[21,22]中，采用重構(gòu)核近似作為近似函數(shù)，基于配點(diǎn)法構(gòu)建離散方程。不失一般性，考慮彈性力學(xué)問題如下，

σi j,j+bi=0inΩ

(14)

σi jnj=hionΠ

(15)

ui=gionΓ

(16)

式中σi j=Ci j k lεk l為應(yīng)力張量，Ci j k l=λδi jδk l+μ(δi kδj l+δi lδj k)為彈性張量，其中拉梅常數(shù)λ=νE/(1+ν)(1-2ν),μ=E/2(1+ν)，E為彈性模量，ν為泊松比，εi j=u(i,j)=(ui,j+uj,i)/2為應(yīng)變張量，ui為位移，Ω為求解域，Π和Γ分別是自然和本質(zhì)邊界，bi為體力，hi和gi為給定的面力和位移，nj為自然邊界Π的外法線方向。

將位移用重構(gòu)核近似函數(shù)離散為

(17)

式中a=[a1,…,aN]T,aI=[ax I,ay I]T

(18)

Φ=[Φ1,…,ΦN],ΦI=ΨII

(19)

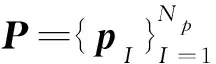
(20)

式中

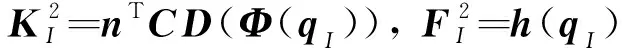
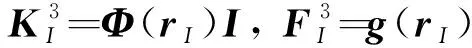
(21)

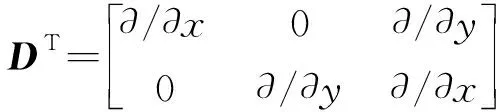
(22)

(23)

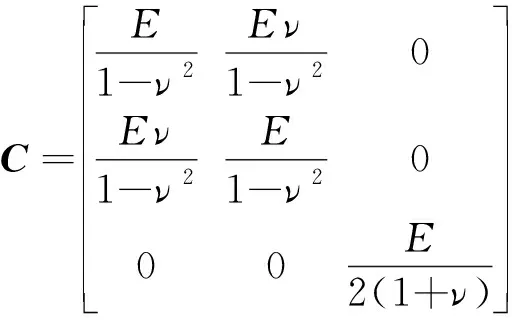
(24)

4 重構(gòu)核粒子法RKPM

重構(gòu)核粒子法RKPM(Reproducing Kernel Particle Method)[7]采用重構(gòu)核近似作為近似函數(shù)，結(jié)合伽遼金法構(gòu)建離散方程。在伽遼金法中，引入權(quán)函數(shù)wi，并在整個問題區(qū)域內(nèi)對控制方程(14)積分得

(25)

采用分步積分并引入散度定理，式(25)可表示為

(26)

考慮自然邊界條件方程(15)，并代入應(yīng)變表達(dá)式得

(27)

代入近似函數(shù)(17)并定義權(quán)函數(shù)的近似函數(shù)為w≈Ψ，式(27)可改寫為

(28)

(29)

(30)

(31)

本質(zhì)邊界條件(16)可以通過拉格朗日乘子法[6]和罰函數(shù)法[28]等方法施加，本文采用拉格朗日乘子法施加本質(zhì)邊界條件。

在數(shù)值計算中，無網(wǎng)格法可以借鑒有限元法的數(shù)值積分模式，將求解區(qū)域離散成相連而互不重疊的背景積分網(wǎng)格Ωl(l=1,2,…,Nl)，在背景積分網(wǎng)格上對剛度矩陣采用高斯積分得

(32)

(33)

同理，將自然邊界離散成相連而互不重疊的背景積分網(wǎng)格Πb(b=1,2,…,Nb)，對載荷矩陣采用高斯積分得

(34)

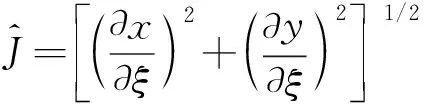
(35)

5 無網(wǎng)格穩(wěn)定配點(diǎn)法

在無網(wǎng)格穩(wěn)定配點(diǎn)法[29]中，首先在求解域及其邊界上布置若干個離散點(diǎn)，以每個離散點(diǎn)為中心構(gòu)建一子域，域內(nèi)子域通常可選用正方形，在子域內(nèi)積分如下。

(36)

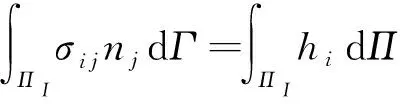
(37)

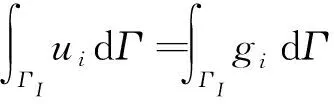
(38)

(39)

(40)

將重構(gòu)核近似位移離散函數(shù)(17)代入式(36～38)，可得

(41)

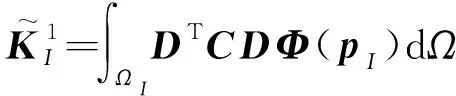
(42)

無網(wǎng)格穩(wěn)定配點(diǎn)法中，在規(guī)則的四邊形子域內(nèi)進(jìn)行高斯積分，可表示為

(43)

(44)

(45)

無網(wǎng)格穩(wěn)定配點(diǎn)法和典型的數(shù)值方法的比較列入表1，發(fā)現(xiàn)穩(wěn)定配點(diǎn)法具有如下優(yōu)點(diǎn)。

表1 典型數(shù)值方法比較Tab.1 Comparison of the numerical methods

(1) 構(gòu)建近似函數(shù)和積分均不需要背景網(wǎng)格，是真正的無網(wǎng)格法。

(2) 在子域內(nèi)容易實現(xiàn)高階準(zhǔn)確積分，積分精度高，效率高。

(3) 積分子域只和離散點(diǎn)的位置有關(guān)，在變形前后均保持規(guī)則形狀。

(4) 滿足局域離散方程守恒，這對于提高流體力學(xué)問題的數(shù)值計算精度和穩(wěn)定性尤為重要。

另外，需要特別說明的是，無網(wǎng)格穩(wěn)定配點(diǎn)法和無網(wǎng)格局部彼得洛夫-伽遼金法(MLPG)都是在子域內(nèi)進(jìn)行積分。不同的是，無網(wǎng)格穩(wěn)定配點(diǎn)法采用的是強(qiáng)形式直接積分；而無網(wǎng)格局部彼得洛夫-伽遼金法采用的是弱形式，引入散度定理，由于采用子域積分，需采用特定的試函數(shù)使得域內(nèi)子域自然邊界條件積分為0以簡化計算，而且其和邊界交界的子域積分也需經(jīng)過特殊處理。此外，無網(wǎng)格局部彼得洛夫-伽遼金法的子域在邊界上可能會截斷，影響計算精度，而無網(wǎng)格穩(wěn)定配點(diǎn)法的子域可以超出計算域，更為自由。因此，無網(wǎng)格局部彼得洛夫-伽遼金法的計算要比無網(wǎng)格穩(wěn)定配點(diǎn)法更為復(fù)雜，且求解精度受積分精度影響，而無網(wǎng)格穩(wěn)定配點(diǎn)法更容易實現(xiàn)準(zhǔn)確積分。

6 數(shù)值算例

在數(shù)值計算中，采用如下的L2和H1誤差來評估算法的精度

(46)

(47)

(i=1,2,…,Nd)(48)

式中RNd(i)∈(-1,1)為服從正態(tài)分布的隨機(jī)數(shù)，Nd為隨機(jī)數(shù)的個數(shù)。定義相對誤差如下，

(49)

(50)

6.1 一維桿問題

考察如圖2所示左端固定的一維桿問題，其控制方程和邊界條件如下。

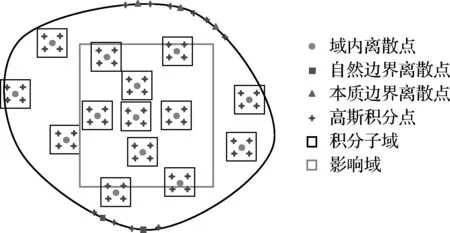
圖1 穩(wěn)定配點(diǎn)法中點(diǎn)的布置

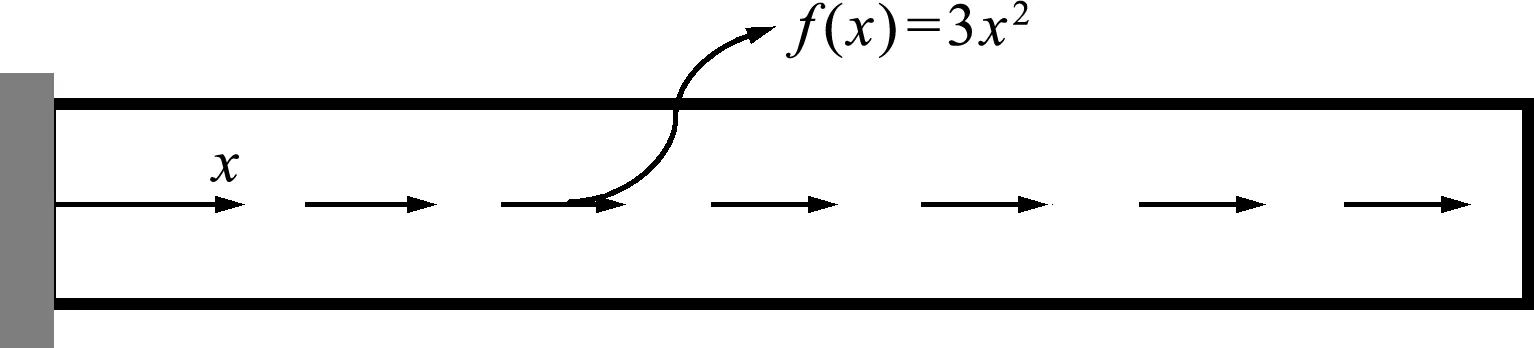
圖2 一維桿

EAu,x x+f(x)=0,u(0)=0,EAu,x(L)=0

(51)

圖3和圖4(相對誤差定義見式(49，50))比較了采用重構(gòu)核配點(diǎn)法、重構(gòu)核粒子法和穩(wěn)定配點(diǎn)法的精度、收斂性和穩(wěn)定性，其中重構(gòu)核粒子法和穩(wěn)定配點(diǎn)法均采用兩點(diǎn)高斯積分，結(jié)果表明穩(wěn)定配點(diǎn)法的精度、收斂率和穩(wěn)定性均優(yōu)于重構(gòu)核配點(diǎn)法和重構(gòu)核粒子法。圖5比較了三種方法的剛度矩陣條件數(shù)，其中穩(wěn)定配點(diǎn)法的條件數(shù)最低，這也使得其具有更好的穩(wěn)定性。從圖6的計算時間比較可以看出，穩(wěn)定配點(diǎn)法和重構(gòu)核配點(diǎn)法的效率均高于重構(gòu)核粒子法。

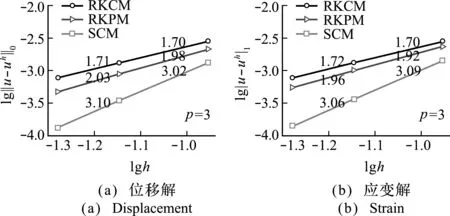
圖3 一維桿問題的數(shù)值計算結(jié)果

圖4 一維桿問題的穩(wěn)定性分析

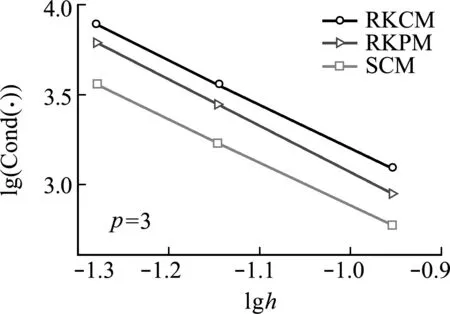
圖5 一維桿問題的剛度矩陣條件數(shù)

圖6 一維桿問題的計算時間

6.2 空心圓筒問題

如圖7所示，無限長空心圓筒受內(nèi)壓為P0=500 N，外壓為P1=500 N，圓筒內(nèi)徑為r0=4 m，外徑為r1=10 m。彈性模量E=2×107Pa，泊松比ν=0.3。由于對稱性，僅采用圓筒的1/4作為數(shù)值計算模型進(jìn)行離散。其控制方程和邊界條件可表示為

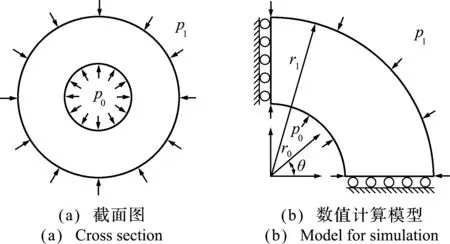
圖7 空心圓筒問題

(52)

式中ti=σi jnj。此問題的解析解為

(53)

圖8和圖9的數(shù)值計算結(jié)果再次表明，穩(wěn)定配點(diǎn)法的精度和穩(wěn)定性均優(yōu)于直接配點(diǎn)法(重構(gòu)核配點(diǎn)法)和伽遼金型無網(wǎng)格法(重構(gòu)核粒子法)，而且其對應(yīng)的剛度矩陣條件數(shù)更低，如圖10所示，這也有利于提高數(shù)值結(jié)果的穩(wěn)定性。圖11的計算時間比較表明，穩(wěn)定配點(diǎn)法的效率略低于直接配點(diǎn)法，明顯優(yōu)于伽遼金型的重構(gòu)核粒子法。

圖8 空心圓筒問題的數(shù)值計算結(jié)果

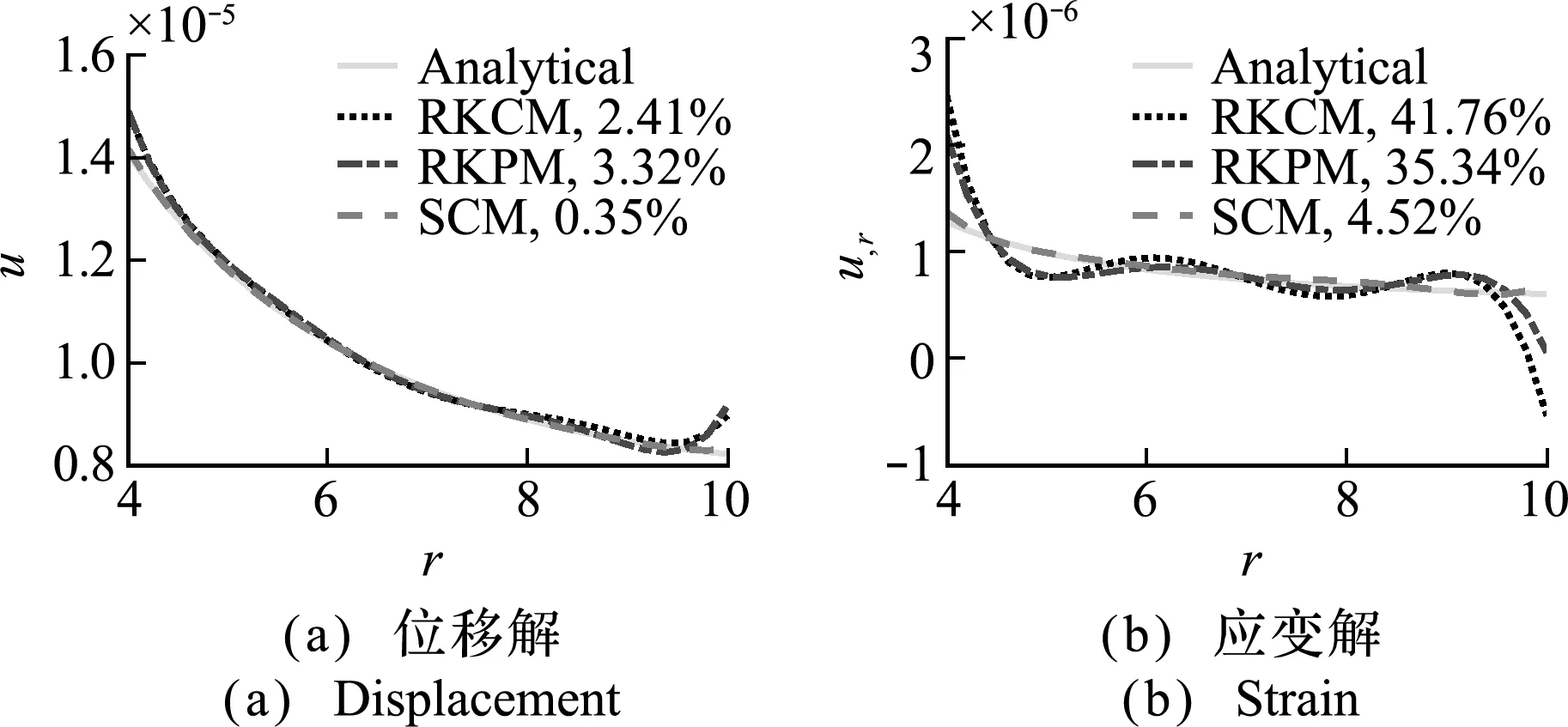
圖9 空心圓筒問題的穩(wěn)定性分析

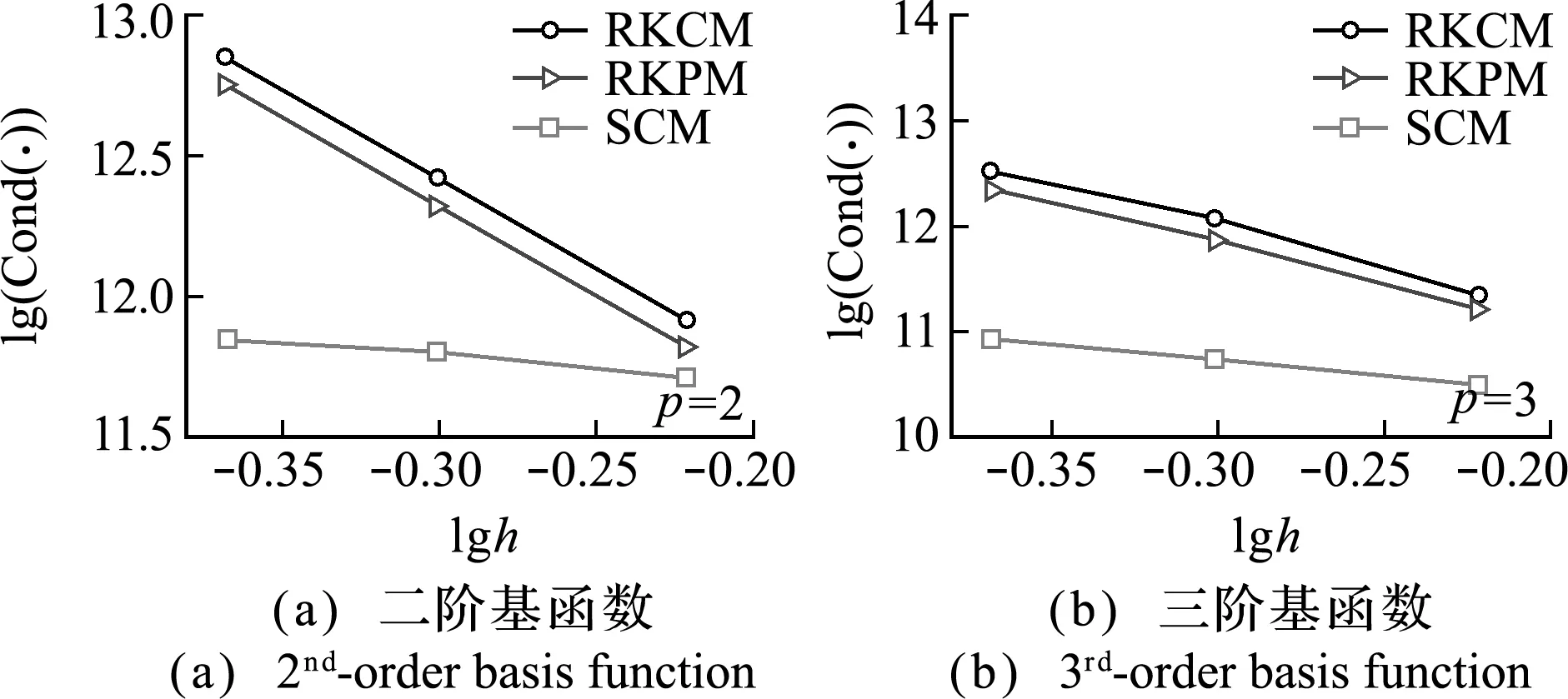
圖10 空心圓筒問題的剛度矩陣條件數(shù)

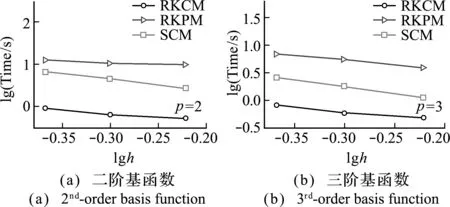
圖11 空心圓筒問題的計算時間

7 結(jié) 論

本文介紹了一種新的無網(wǎng)格法,即無網(wǎng)格穩(wěn)定配點(diǎn)法，該方法不需要網(wǎng)格構(gòu)建近似函數(shù)，也不需要背景網(wǎng)格進(jìn)行積分，是一種真正的無網(wǎng)格法。由于子域都是規(guī)則的正方形，采用高斯積分可以實現(xiàn)準(zhǔn)確積分，提高了算法的精度和穩(wěn)定性，而且子域積分有利于降低離散矩陣的條件數(shù)，進(jìn)一步提高了算法的穩(wěn)定性。由于對應(yīng)積分子域只和配點(diǎn)位置有關(guān)，和問題求解區(qū)域形狀以及變形均無關(guān)，對于大變形和局部高梯度等復(fù)雜問題[18]同樣適用，對于任何問題，積分子域都是規(guī)則子域而不會發(fā)生變形。相較于直接配點(diǎn)型無網(wǎng)格法，穩(wěn)定配點(diǎn)法通過準(zhǔn)確子域積分提高了精度和穩(wěn)定性，積分非常高效，仍然保持配點(diǎn)型無網(wǎng)格法的高效性。相較于伽遼金型無網(wǎng)格法需要在全域內(nèi)積分，而且難以實現(xiàn)準(zhǔn)確積分，穩(wěn)定配點(diǎn)法只需要在局部子域進(jìn)行積分，而且通過傳統(tǒng)高斯積分就可以實現(xiàn)高階準(zhǔn)確積分，所以比伽遼金型無網(wǎng)格法具有更高的效率。彈性力學(xué)算例的數(shù)值計算結(jié)果展示了該方法精度高、效率高和穩(wěn)定性好的優(yōu)點(diǎn)。由于穩(wěn)定配點(diǎn)法的基本方法是子域法，與有限體積法一樣滿足局部離散方程守恒，因此其在流體力學(xué)和流固耦合分析中具有較大潛力，未來將進(jìn)一步拓展這些方面的應(yīng)用研究。