非線性動力方程精細積分法的自適應(yīng)步長研究
王海波, 紀海潮
(中南大學(xué) 土木工程學(xué)院,長沙 410075)
1 引 言
鐘萬勰[1]提出的精細積分方法,為非線性系統(tǒng)的時程分析開辟了嶄新的途徑;趙秋玲[2]提出了一種非線性系統(tǒng)線性化的精細積分法;張洵安等[3]提出了一種精度較高的線性化迭代精細積分方法;裘春航等[4]將非線性部分用j次多項式來近似;李金橋等[5]先將非線性部分在tk時刻展開成泰勒級數(shù)形式,然后將非線性積分項采用泰勒展開法或高斯-勒讓德數(shù)值積分法與精細積分法結(jié)合進行求解;王海波等[6]將精細積分法與Adams-Bashforth-Moulton多步法相結(jié)合,提出了一種高精度和高效率的精細積分多步法;李緯華等[7]利用改進的歐拉法對狀態(tài)變量進行預(yù)估及校正,然后結(jié)合辛時間子域法對非線性方程進行求解;江小燕[8]根據(jù) Hamilton 變作用定律構(gòu)造了時空有限元矩陣,提出了求解非線性動力方程的精細時空有限元法;王海波等[9]結(jié)合精細積分法和Romberg數(shù)值積分,提出了一種避免狀態(tài)矩陣求逆的高效精細積分單步法;梅樹立等[10]利用龍貝格積分法的自適應(yīng)性解決時間步長的選擇問題,提出了結(jié)構(gòu)非線性動力方程的自適應(yīng)精細積分算法;李健等[11]基于積分區(qū)間逐次半分的思想實現(xiàn)了任意時間步長的自適應(yīng)求積。
本文基于Adams顯式和隱式預(yù)估公式實現(xiàn)對時間步長的自適應(yīng)選擇,使得時間步長依賴于給定的誤差限值。算例證明該思想可以應(yīng)用于預(yù)估型(求解過程需要用到預(yù)估公式)精細積分算法,能有效提高計算精度,同時使得算法具有很好的穩(wěn)定性,能解決剛度軟化和剛度硬化問題,具有廣泛的適用性。
2 自適應(yīng)步長的實現(xiàn)原理
2.1 非線性動力方程
非線性動力方程可以表示為
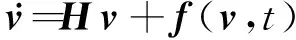
(1)
利用文獻[1]的指數(shù)矩陣可將其轉(zhuǎn)化為如下同解積分方程,
(2)
式中v(tk + 1)和v(tk)分別為所求解向量在時刻tk + 1和tk的值。
對于式(2),第一項可直接采用精細算法精確得到,計算精度非常高,因此誤差的主要來源是對第二項的處理。對于第二項,精細積分算法會用到預(yù)估公式,如文獻[6,9](先對v(tk + j / 4)(j=1,2,3,4)進行預(yù)估,再進行數(shù)值積分的一種精細積分算法)。
為數(shù)學(xué)上敘述方便,對積分方程(3)進行討論。
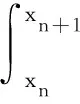
(3)
2.2 Adams顯式與隱式預(yù)估公式
設(shè)由r+1個已知的數(shù)據(jù)點(xn,fn),(xn - 1,fn - 1),…,(xn - r,fn - r)構(gòu)造插值多項式pr(x),其中fk=f(xk,yk),xk=x0+kh(h為時間步長),運用插值公式有
(4)
(5)
得到r+1階Adams顯式公式,
(6)
(j=0,1…,r)
同理,由r個已知的數(shù)據(jù)點(xn,fn),(xn - 1,fn - 1),…,(xn - r + 1,fn - r + 1)以及一個未知的數(shù)據(jù)點(xn + 1,fn + 1),構(gòu)造插值多項式pr(x),就可以得到r+1階Adams隱式公式。
2.3 Adams公式的局部誤差
y(xn + 1)為真實值,yn + 1為基于預(yù)估公式對y(xn + 1)的預(yù)估值,誤差函數(shù)Tn + 1=y(xn + 1)-yn + 1。
構(gòu)造如下具有p階精度的預(yù)估公式:
yn + 1=α0yn+α1yn - 1+…+αryn - r+
h(β-1fn + 1+β0fn+…+βrfn - r)
(7)
(8)
式(8)右端各項在點xn處作Taylor展開,整理得
y(p + 1)(xn)+O(hp + 2)
(9)
當參數(shù)αk和βk滿足式(10)時,預(yù)估公式達到p階精度。
(10)
當r=3,p=4,取β-1=0,α1=α2=α3=0,由式(10)可得出其他待定參數(shù)的方程組,解之得
(11)
(12)
式(11)是四階精度的Adams顯式公式,式(12)是其截斷誤差。同理可以得出各階精度Adams 公式的局部截斷誤差主項,列入表1。

表1 局部截斷誤差主項Tab.1 Local truncation error main term
2.4 誤差估計及其優(yōu)點
使用Adams顯式公式進行預(yù)估,將其結(jié)果作為已知的數(shù)值點代入Adams隱式公式,再利用Adams顯式與隱式公式的局部誤差公式,即可得到對一個時間步長的誤差估計,下面以四階精度的Adams顯式公式和隱式公式為例。
(13)
fn - 2]
(14)
(15)
(16)
(17)
ξ(xn + 1)=max[abs(ξ′(xn + 1))]
(18)
(19)
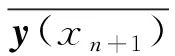
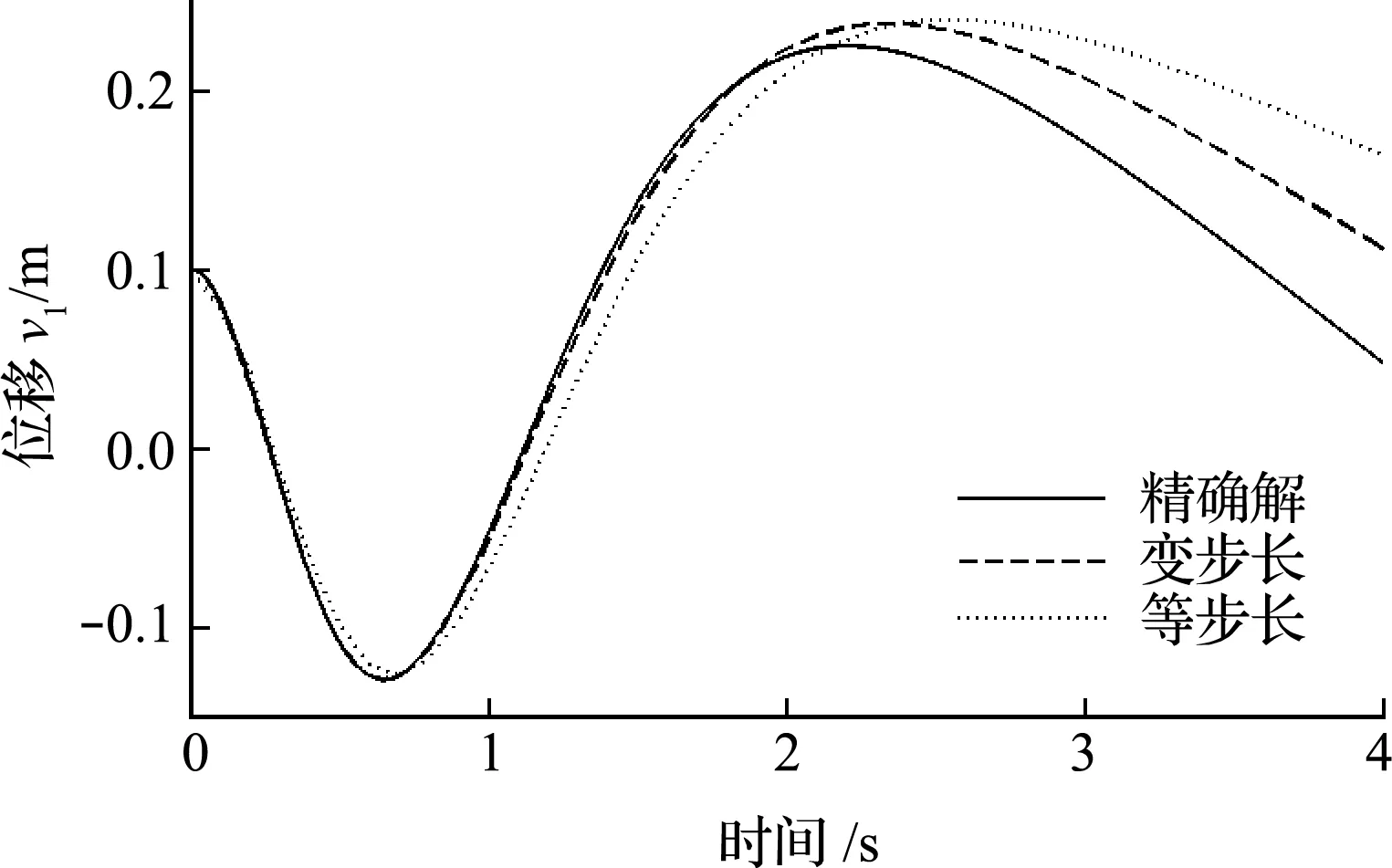
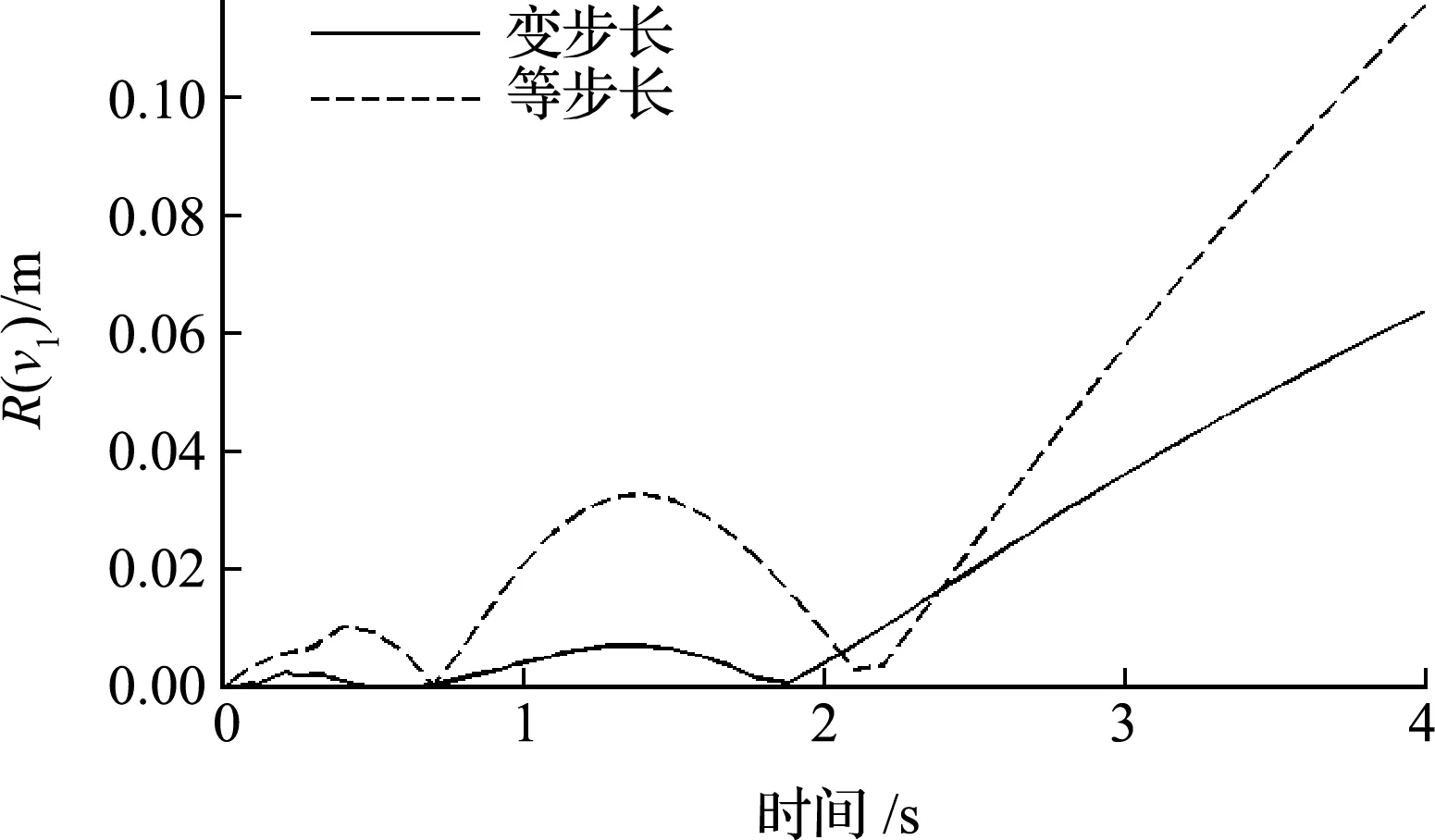
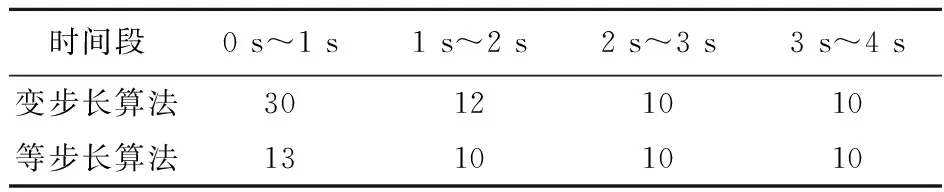
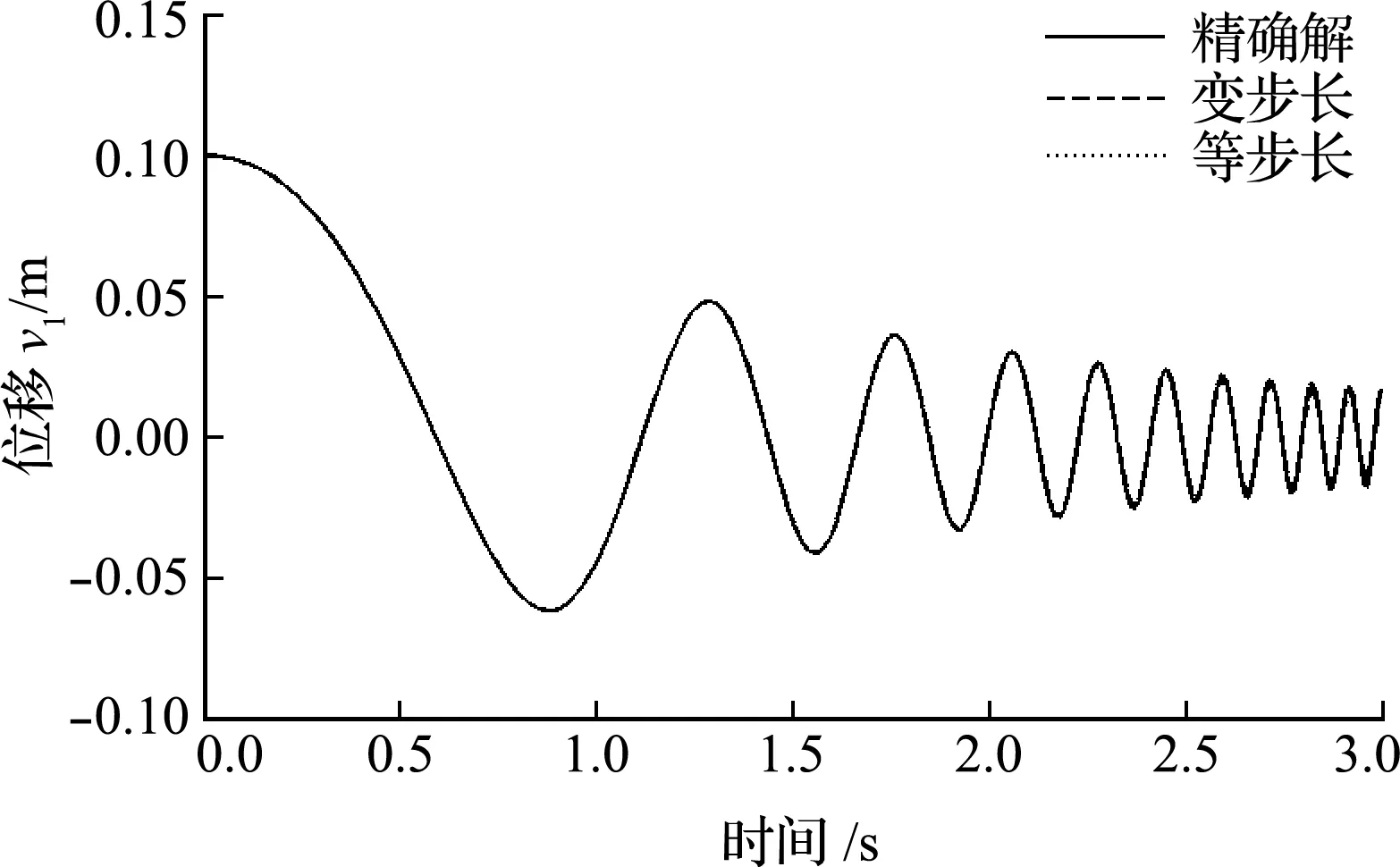
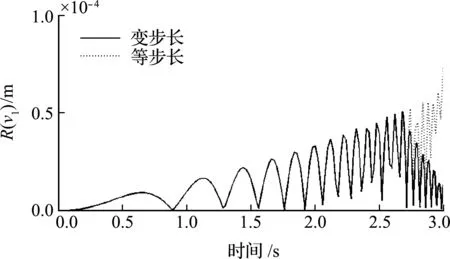
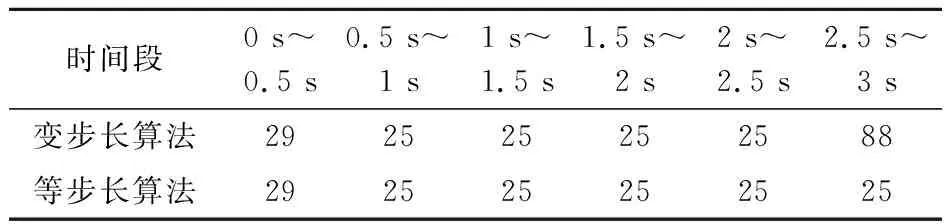
計算時,可調(diào)節(jié)計算步長,使ξ(xn + 1) (1) 通過選擇r+1階Adams公式及誤差限值a,理論上可以實現(xiàn)任意精度的計算結(jié)果。 (2)ξ(xn + 1) (3) 式(14~19)的系數(shù)均是小于1的數(shù),在進行重復(fù)計算時,使得計算誤差不會累計擴大,具有良好的穩(wěn)定性。 在精細積分算法中,預(yù)估環(huán)節(jié)應(yīng)用本文第2節(jié)的內(nèi)容,即可實現(xiàn)自適應(yīng)時間步長,本節(jié)以四階精度的Adams公式進行說明。 a的取值決定求解的時間步,進而影響求解精度與效率,在給定a值時,要注意每步局部誤差的大小與采用的Adams公式的精度有關(guān),如對于四階精度的Adams公式,其局部誤差的大小是時間步長的5次方。在選定a值時,要根據(jù)實際問題允許的誤差范圍,再結(jié)合采用的Adams公式的精度及所希望的時間步長范圍綜合考慮。 b為根據(jù)結(jié)構(gòu)非線性程度控制時間步長縮小的參數(shù),可以在不同的時段內(nèi)設(shè)置不同的b。當函數(shù)的階數(shù)越高,就需要越多的控制點才能準確描繪出曲線。求解非線性動力方程得到時程曲線,進而得到位移-時間的函數(shù)關(guān)系,當某一時間段內(nèi)的函數(shù)階數(shù)較高時,即非線性程度較高時,可以取較小的b值,結(jié)果是所取時間步長會較小,該時間步長內(nèi)的函數(shù)階數(shù)就會相應(yīng)降低,預(yù)估的結(jié)果更加準確。 圖1 算法流程 為便于說明基于Adams顯式和隱式預(yù)估公式實現(xiàn)對時間步長的自適應(yīng)選擇思想在精細積分算法中的應(yīng)用,選擇以文獻[6]為基礎(chǔ),其步驟簡單,思路清晰。 采用四階精度的Adams公式對式(2)的v(tk + 1)進行預(yù)估, P(tk+1)=eH Δ tv(tk)+wk (20) 37F(tk - 2)-9F(tk - 3)] (21) (i=0,1,2,3)(22) Ej=eH (tk - j + 1-tk - i) (j=0,1,2,3)(23) 式中Ej(j=0,1,2,3)采用精細算法[1]精確得到。 (24) 令F(tk + 1)=f[m(tk + 1),tk + 1], (25) F(tk - 3)] (26) (27) 給定誤差限值a,根據(jù)ξ(tk + 1)進行判斷, (1) 當ξ(tk + 1)≤a時 (28) 進入下一時間步的計算。 (2) 當ξ(tk + 1)>a時,令 Δt=bΔt,E0=eH Δ t (29,30) 返回式(20)重新進行計算。 式(24)的(Ck-Pk)存在起步問題,對v(t5)進行計算時,令C4=0,P4=0,其做法對結(jié)果的影響可以忽略不計。 本方法為多步法,需要用單步法計算表頭。 注意,等步長算法是文獻[6]提出的一次預(yù)估-校正精細積分多步法(Δt=0.1 s);變步長算法是以文獻[6]提出的一次預(yù)估-校正精細積分多步法為基礎(chǔ)的自適應(yīng)步長精細積分算法(a=0.0001 m,b=0.5,Δt=0.1 s)。 圖2中,精確解是指積分步長縮小至能計算出有效位數(shù)(一般取小數(shù)點后8位)相同的計算結(jié)果,下同。 圖2 位移時程曲線 從圖2和圖3可以看出,變步長算法的精度比等步長算法的精度高;由表2可知,在0 s~1 s的時間段內(nèi),變步長算法的時間步長小于等步長算法的時間步長;證明了基于顯式和隱式預(yù)估公式實現(xiàn)對時間步長的自適應(yīng)選擇的思想對預(yù)估型精細積分算法的有效性,根據(jù)給定的誤差限值來決定時間步長的大小,即根據(jù)非線性程度的大小決定時間步長的大小,從而提高非線性程度較大時間段內(nèi)的精度,進一步提高整體的計算精度。 圖3 解的絕對誤差 表2 各時間段包含時間節(jié)點的個數(shù) 本節(jié)的等步長算法是文獻[9]提出的精細積分法(Δt=0.02 s);變步長算法是以文獻[9]提出精細積分法為基礎(chǔ)的自適應(yīng)步長精細積分算法(a= 0.0001 m,b= 0.5,Δt=0.02 s)(文獻[9]所述精細積分法在每個時間步長中需要對v(tk + j / 4)(j=1,2,3,4)進行預(yù)估,可得出ξ(tk + j / 4)(j=1,2,3,4),本文令ξ(tk + 1)=ξ(tk + 1/4)+ξ(tk + 1/2)+ξ(tk + 3/4)+ξ(tk + 1))。 圖4 位移時程曲線 圖5 解的絕對誤差 表3 各時間段包含時間節(jié)點的個數(shù) 算例1是剛度軟化問題,算例2是剛度硬化問題,而且算例1與算例2分別以文獻[6,9]提出的預(yù)估型精細積分法為基礎(chǔ),兩個算例均有很好的效果,故基于Adams顯式和隱式預(yù)估公式實現(xiàn)對時間步長的自適應(yīng)選擇的思想具有廣泛的適用性。 (1) 本文將基于Adams顯式和隱式預(yù)估公式實現(xiàn)對時間步長的自適應(yīng)選擇思想應(yīng)用于精細求積算法中,使得算法的計算精度依賴于給定的誤差限值,故能根據(jù)非線性程度的大小控制時間步長的大小,有效提高非線性程度較大的時間段內(nèi)的精度,從而提高整體的計算精度。對于初始時間段內(nèi)非線性程度較大的問題,該思想更加有效。 (2) 應(yīng)用基于顯式和隱式預(yù)估公式實現(xiàn)對時間步長的自適應(yīng)選擇的思想能使精細積分算法具有很好的穩(wěn)定性。 (3) 本文思想應(yīng)用于精細積分算法中,能解決剛度硬化和剛度軟化等問題,具有廣泛的適用性。3 自適應(yīng)時間步長精細積分算法
3.1 流程圖及參數(shù)分析
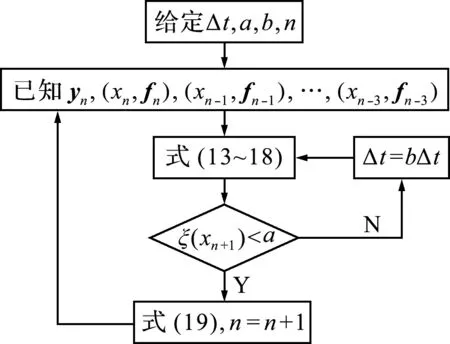
3.2 文獻[6]+自適應(yīng)步長
4 數(shù)值算例
4.1 算例1

4.2 算例2
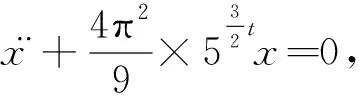
5 結(jié) 論

