基于數據驅動模型求解熱傳導反問題

陳豪龍, 柳占立

(清華大學 航天航空學院 應用力學教育部實驗室，北京 100084)

1 引 言

熱傳導反問題是采用物體內部或表面的溫度信息來反求物體的某些未知信息，如熱物性參數、幾何形狀、邊界條件以及熱源項等。熱傳導反問題在化工、材料、航天、無損探傷、動力工程、冶金工程和生物工程等領域有著廣泛的應用。

熱傳導反問題屬于典型的不適定性問題[1,2]。通常求解熱傳導反問題的方法有Tikhonov正則化[3]、梯度類算法[4,5]和元啟發式優化算法[6,7]等。正則化方法用一組與原不適定問題相鄰近的適定問題的解去逼近，從而降低反問題的不適定性；而迭代類算法是通過搜索待演變量，找到使計算溫度和測量溫度分布最接近的變量作為待求的解。但是迭代類算法在求解過程中需要不斷更新搜索變量，特別是對于邊界幾何形狀識別問題，需要對域內網格重剖分。文獻[8]提出了一種基于參數轉化的思想，將邊界幾何形狀識別問題轉化為有效導熱系數的識別問題，從而避免了域內網格的重剖分，提高了計算效率。但是，這種方法結合迭代類算法在求解反問題過程中，并沒有使用歷史數據信息，對于不同問題，需要重復計算。

近年來，隨著計算機科學的發展，機器學習和數據科學取得了長足進步[9]。借助數據驅動模型，能夠降低與本構模型相關的人力和時間成本，極大地拓展工程師分析力學的能力和進行數值計算的效率，特別是針對特定的力學問題[10,11]。

本文采用數據驅動模型求解熱傳導反問題。首先，使用有限元法求解熱傳導正問題，并利用隨機模型產生訓練數據。在此基礎上，運用有效導熱系數轉化的思想，建立深度學習模型，求解了測點溫度與有效導熱系數之間的抽象映射關系，進而識別了管道內壁的幾何形狀。并進一步擴展深度學習模型，識別了皮膚腫瘤的生長參數，同時討論了不同測量誤差對計算結果的影響。

2 數據驅動基本理論

2.1 人工神經網絡ANN

ANN(Artificial Neural Network)是一種受自然啟發的模擬生物神經網絡模型的方法，因其具有優良的擬合性能，逐漸成為機器學習的主流技術之一。首先簡要介紹ANN的基本原理。

ANN的核心思想是構建一個含有大量待定參數的網絡系統，并通過梯度下降法尋求最佳的網絡參數，從而使誤差函數最小。ANN中包含許多神經元。一組神經元中的每個神經元都與另一組神經元相連。圖1是ANN中單個神經元的數學模型。xi為輸入元素，ωi j為權重，bj為偏差，則輸入與權重的乘積X可以表示為

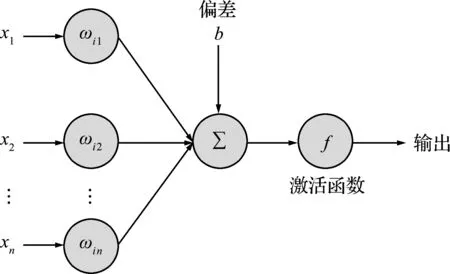
圖1 神經元的數學模型

(1)

然后通過激活函數f產生輸出

(2)

常用的非線性激活函數包括ReLU和Tansig。

如圖2所示，ANN的基本結構由三種類型的層組成，分別為輸入層、隱藏層和輸出層。ANN可以不需要任何額外的信息，尋找輸入層和輸出層之間的抽象映射關系，這個過程叫做訓練。在訓練過程中，根據相應的輸入和輸出(訓練集)來確定網絡中不同層次神經元的權重ωi j和偏差bj等網絡參數。重復訓練過程，直到損失函數值下降到一個可接受的范圍，從而確定網絡參數。損失函數定義為

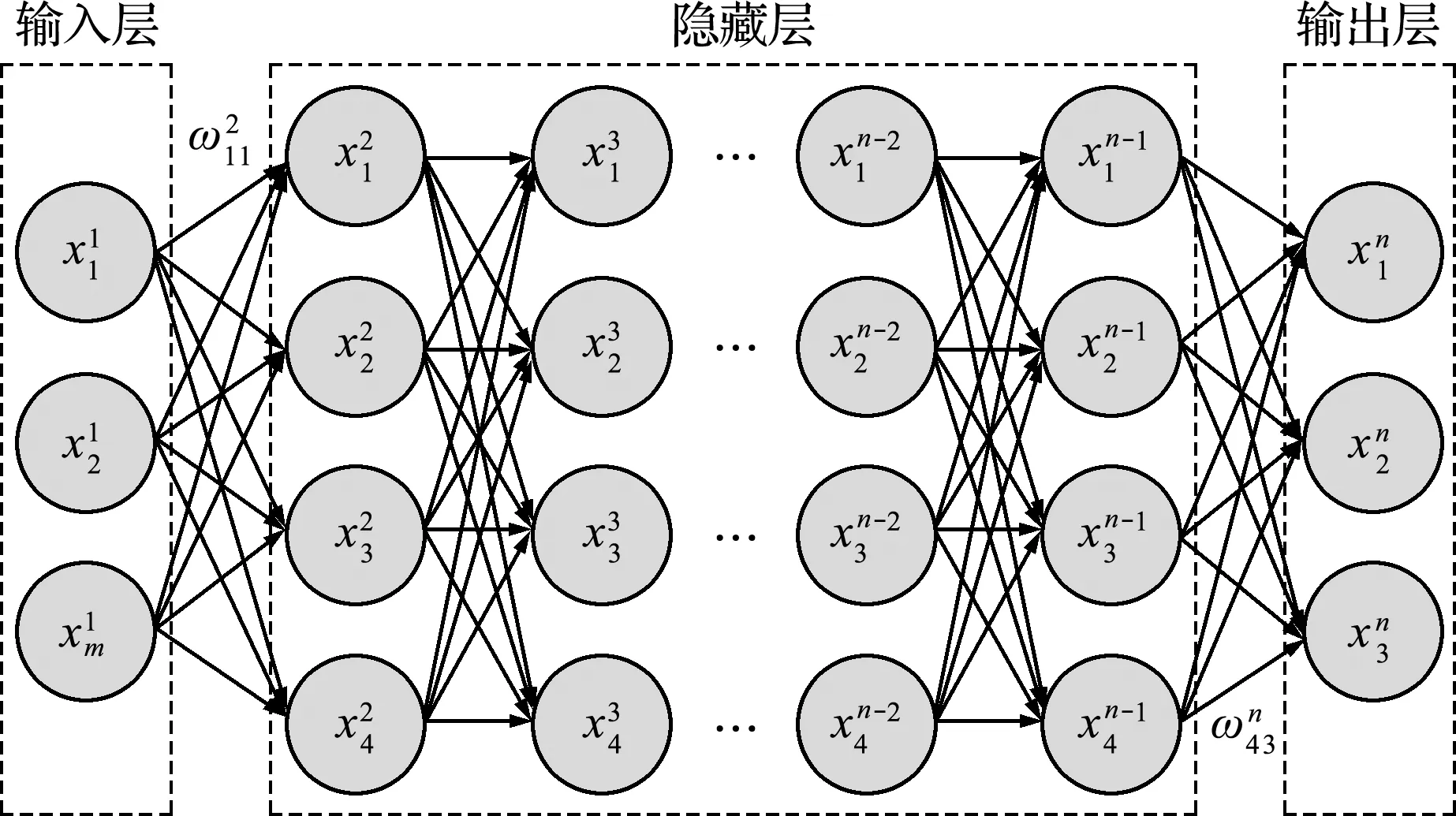
圖2 ANN的結構

(3)

梯度下降法是一種求解損失函數最小值的有效方法。假設L是向量v的函數，則L的變化可以用v的微小變化來近似,即

ΔL=L·Δv

(4)

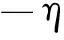
(5)

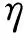
(6)

式中上標k為訓練次數。一般來說，訓練ANN的方法有隨機梯度下降法SGD、均方根傳播算法RMPprop以及自適應梯度算法Adam等。本文采用Adam訓練ANN。

雖然訓練ANN過程耗時較長，但在激活階段能夠根據輸入快速計算輸出，不需要任何迭代過程。需要指出的是，在求解熱傳導反問題過程中，網絡的輸入為溫度數據，輸出則為未知參數或函數。

2.2 卷積神經網絡CNN

CNN(Convolutional Neural Network)是ANN的一個重要分支，主要具有以下特點，同一個卷積層的所有神經元共享一組相同的權重和偏差；每一層只有部分神經元與下一層的神經元連接；在卷積層之后引入池化層。CNN的結構如圖3所示。可以看出，CNN的結構與傳統的ANN非常相似，不同的是，神經元之間的連接是空間稀疏的。

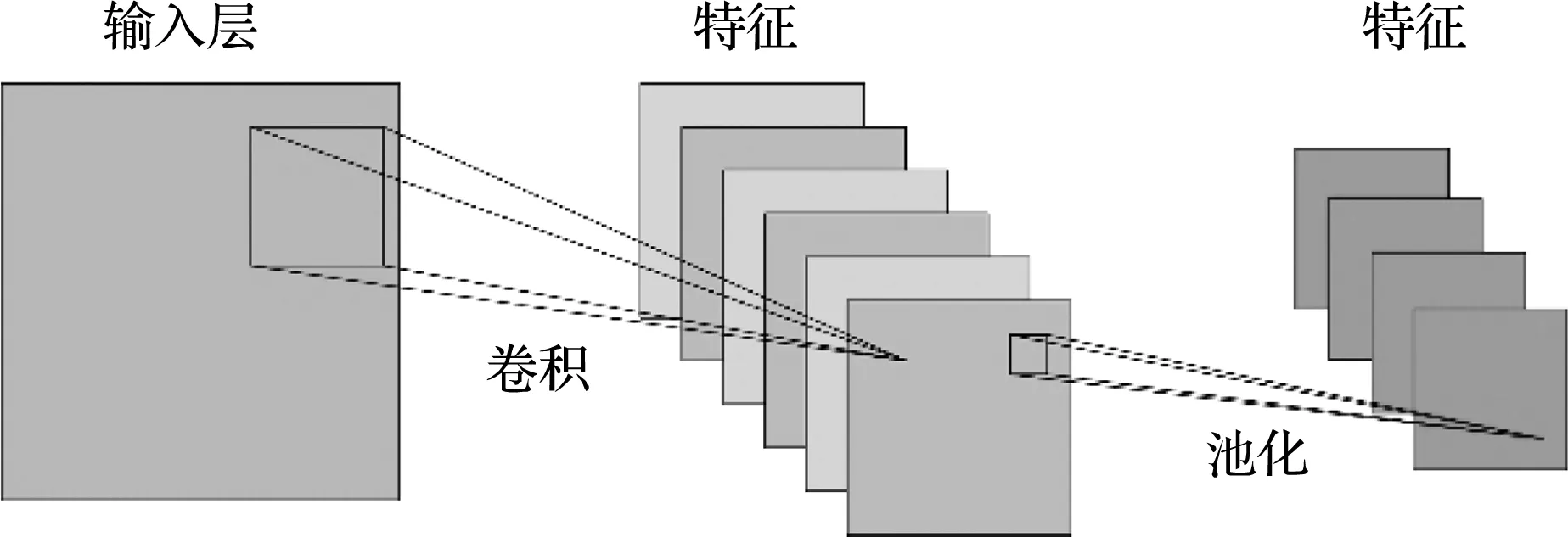
圖3 CNN的結構

在卷積運算中，卷積核作為一個濾波器，應用于輸入層的所有空間，以提取每個空間位置的特征。此外，前一層的特征可以由卷積核獲得，更復雜的特征由后一層的卷積核得到，然后進行池化操作。經卷積和池化后的每個特征都與全連接層相連，這些層之間的連接與ANN相同。

2.3 自動編碼器AE

自20世紀80年代以來，機器學習領域中AE(Auto Encoder)的概念就一直廣受關注。AE通常由編碼器和解碼器兩個部分組成，有如下特點，(1) 有損壓縮和解壓數據；(2) 提取數據特征；(3) 對數據本身進行學習。AE的結構如圖4所示。

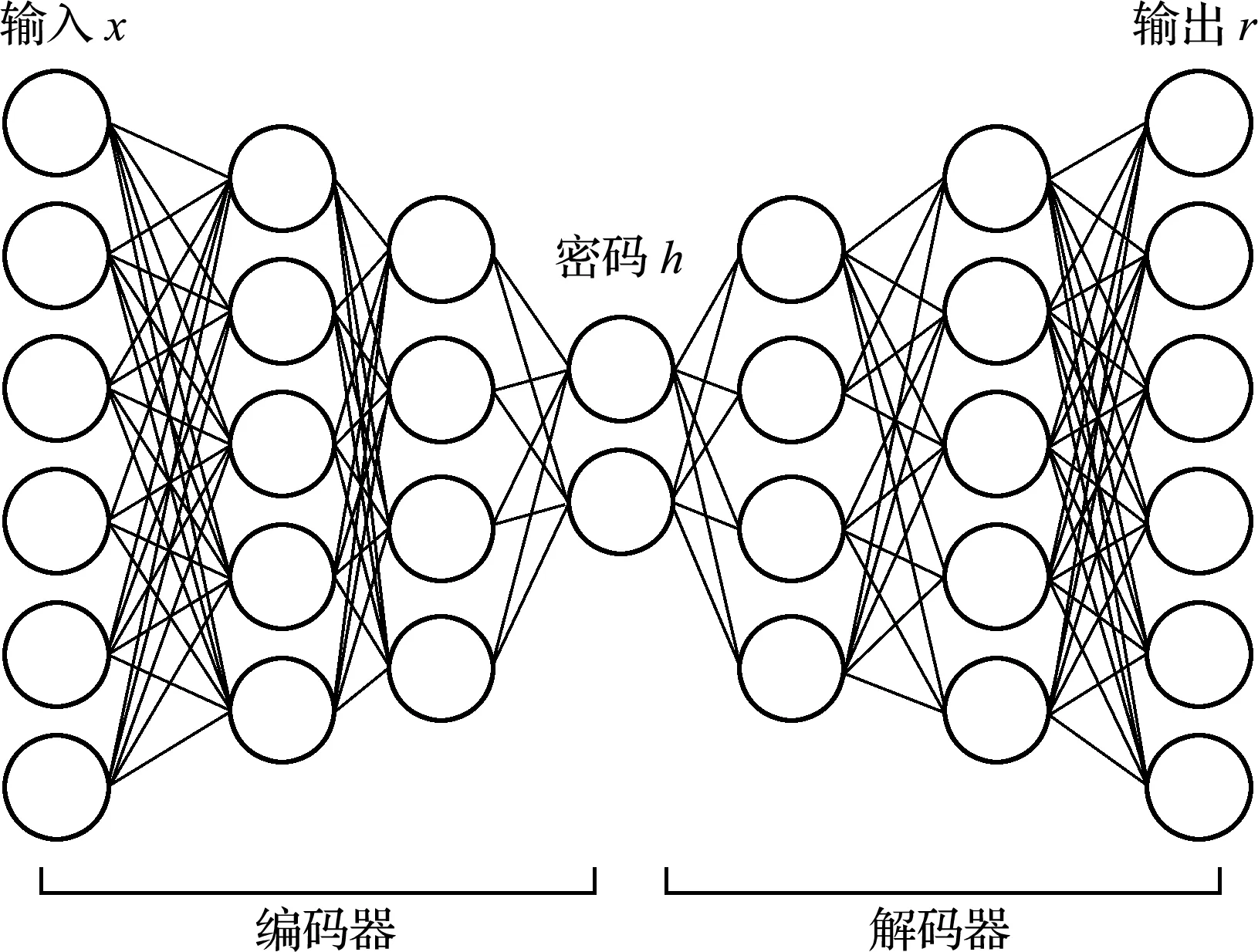
圖4 AE的結構

AE的基本思想是構建一個與輸入具有相同維度的輸出層。編碼器函數可以表示為

h=f(x)

(7)

式中h為密碼。將密碼h傳遞給解碼器，可以重構得到數據r。解碼器函數可以表示為

r=g(h)=g(f(x))

(8)

給定AE的損失函數如下，

(9)

式中S為輸出層參數的個數。本文編碼器的作用是提取數據特征，解碼器的作用是從特征中復現樣本數據。

3 數據驅動求解熱傳導反問題

3.1 管道內壁識別問題[11]

管道內壁識別問題的模型如圖5所示。假定管道外壁的半徑為定值r1，管道內壁的半徑r2是極角θ的函數，導熱系數為常數k0。則管道熱傳導問題的控制方程表示為

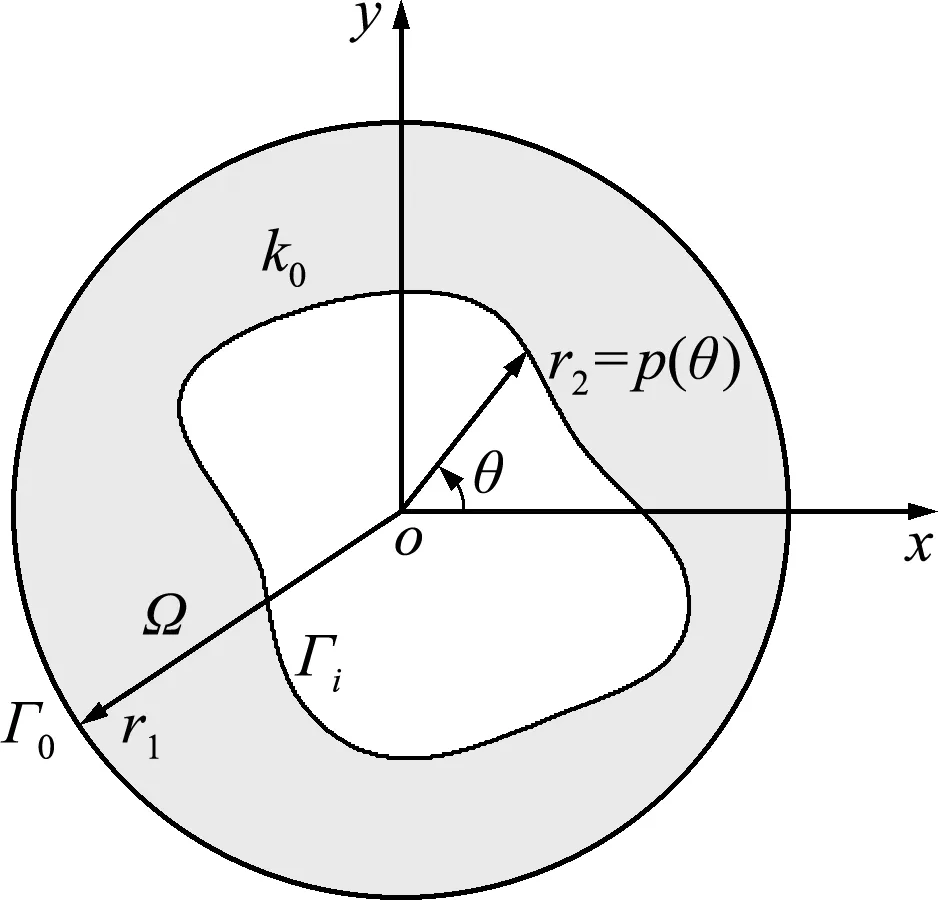
圖5 管道內壁識別幾何模型

(10)

給定邊界條件如下,

T(r,θ)=Tatr=r2

(11)

-k0[?T(r,θ)/?r]=qatr=r1

(12)

在幾何形狀識別問題中，除管道內邊界形狀r2=p(θ)未知外，所有參數和邊界條件均已知。管道內壁幾何形狀識別問題的目標是通過測量表面或區域內的溫度來反求管道內壁的幾何形狀。

本文采用一種轉換方法如圖6所示，在求解過程中，將未知的邊界幾何形狀轉換為規則形狀，但導熱系數是邊界坐標的函數。然后,將幾何形狀識別問題轉化為有效導熱系數的識別問題，從而避免了求解過程中網格的重構。有效導熱系數可計算為

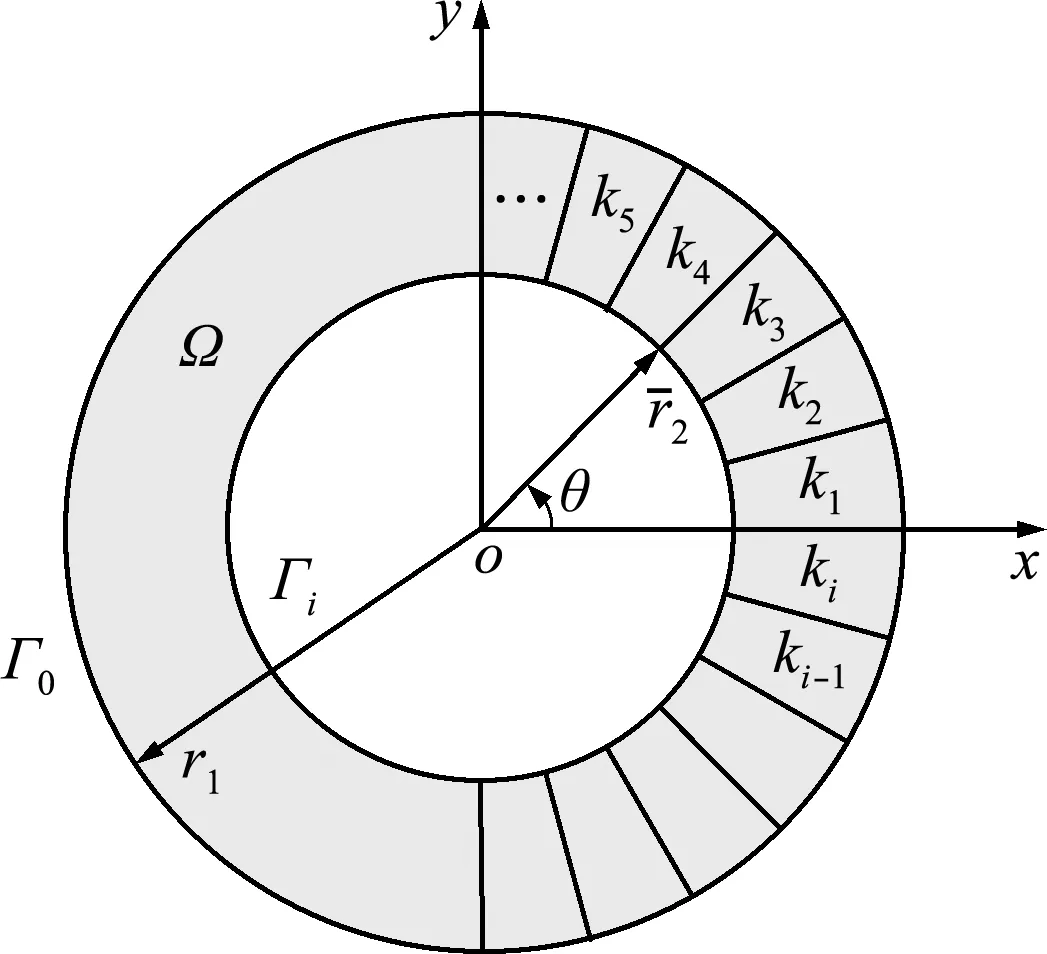
圖6 轉換后的管道模型

(13)

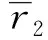
然后,將原問題轉化為求解功能梯度材料的熱傳導問題，控制方程為

(14)

式中k為式(13)的有效導熱系數，同樣給定邊界條件為式(11,12)。

得到有效導熱系數后，經轉換，可得未知的邊界幾何形狀為

(15)

管道內壁識別的流程如圖7所示。所有算例都在3.4 GHz CPU(Interl Xeon E5-1680 v4 128.00 GB RAM)的個人計算機上進行。

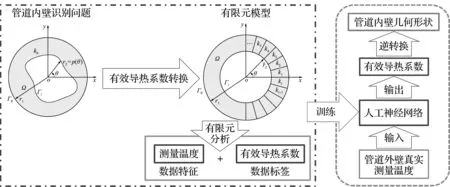
圖7 管道內壁識別的計算流程

3.1.1 測量誤差對計算結果的影響

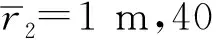
(16)

討論不同隱藏層數和訓練次數對計算結果的影響，隱藏層分別取2,3和4，訓練次數分別設置為500次、1000次和2000次，使用隨機產生的5000個模型作為訓練樣本。計算結果的損失函數值列入表1。

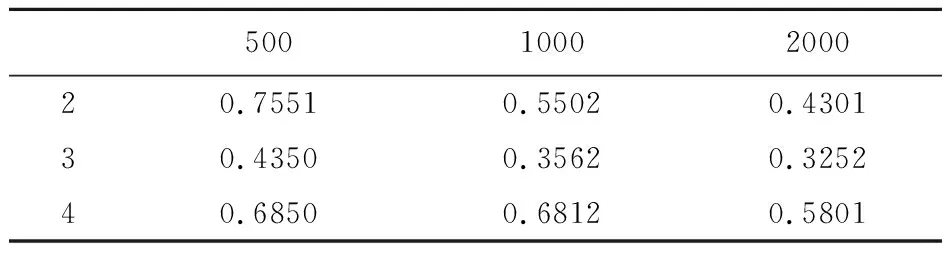
表1 不同隱藏層及訓練次數的損失函數值

由表1可知，隨著訓練次數的增加，損失函數值逐漸減小。當隱藏層數為3時，經過2000次訓練得到的損失函數值最小。所以，在后續的計算中設置隱藏層數為3，訓練的次數為2000次。

討論不同測量誤差對計算結果的影響。測量誤差分別取為1%和5%。表2和圖8給出了不同測量誤差的反演結果，圖9展示了反演結果的相對誤差。

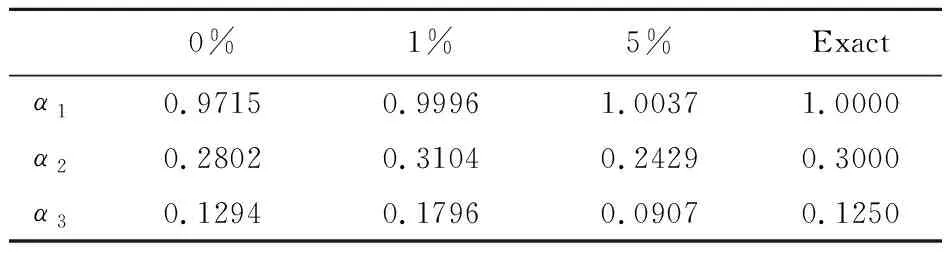
表2 不同測量誤差時參數的反演結果

表2表明，在不考慮測量誤差的情況下，反演結果與精確解非常接近。隨著測量誤差的增加，反演結果偏離精確解。從圖8和圖9可以看出，隨著測量誤差的增加，反演結果愈加偏離精確的邊界形狀，相對誤差變大。在測量誤差為5%時，仍然可以得到較為準確的反演結果。

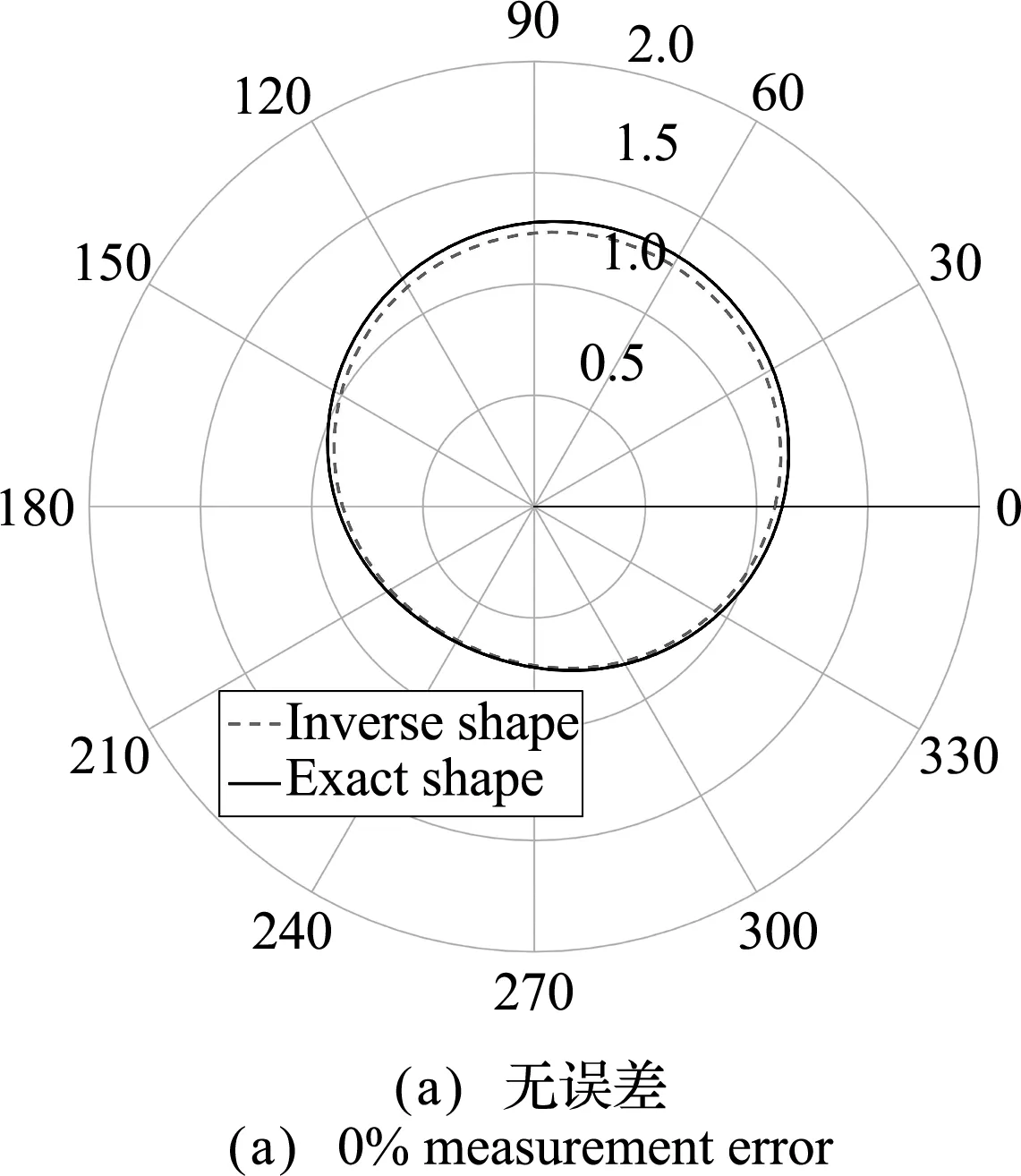
圖8 不同測量誤差的反演結果

圖9 不同測量誤差時，反演結果的相對誤差

3.1.2 測點數量對計算結果的影響

考慮一個橢圓管道內壁，橢圓的長軸和短軸分別為 1.5 m 和 1.0 m。真實的管道內邊界幾何形狀可以表示為

式中α1=1.5,α2=1.0,α3=0.25。討論不同測點數量對計算結果的影響。如圖10所示，分別采用10個、20個和40個測點。轉化后的有效導熱系數可以表示為

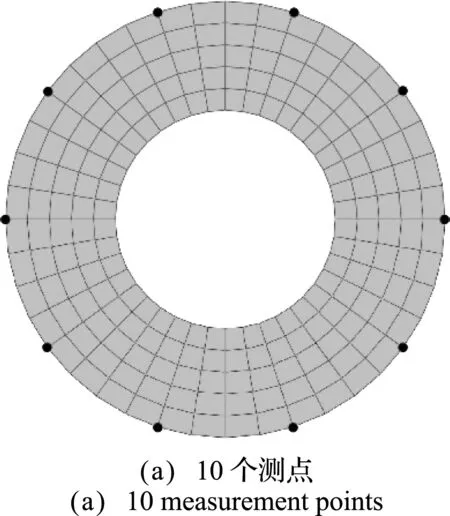
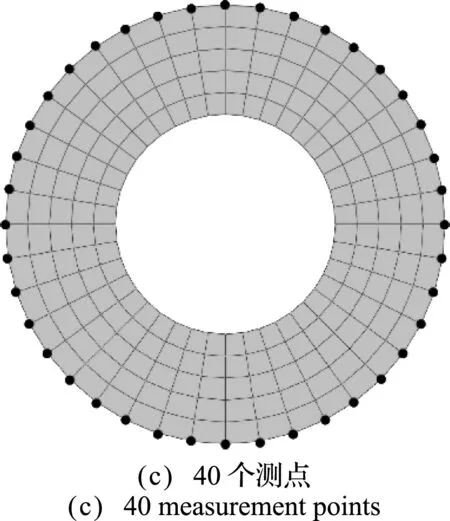
圖10 不同測點數量的有限元模型

(17)

反演結果列入表3，反演得到的管道內邊界形狀如圖11所示。圖12展示了反演結果的相對誤差。表3表明，計算結果與精確解較為吻合。從 圖11 和圖12可以看出，隨著測點數量的增加，反演結果更接近于準確的幾何形狀，反演結果的相對誤差變小。

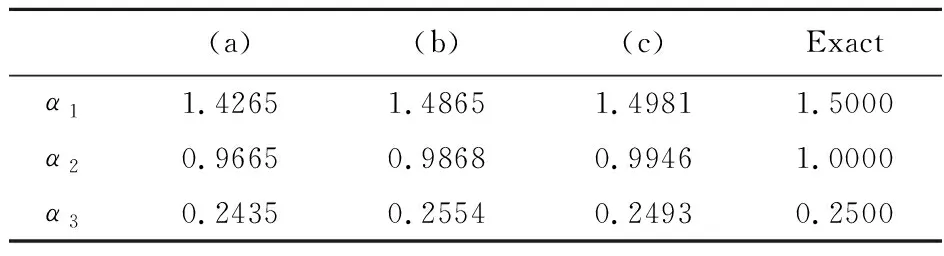
表3 不同測點數量的反演結果

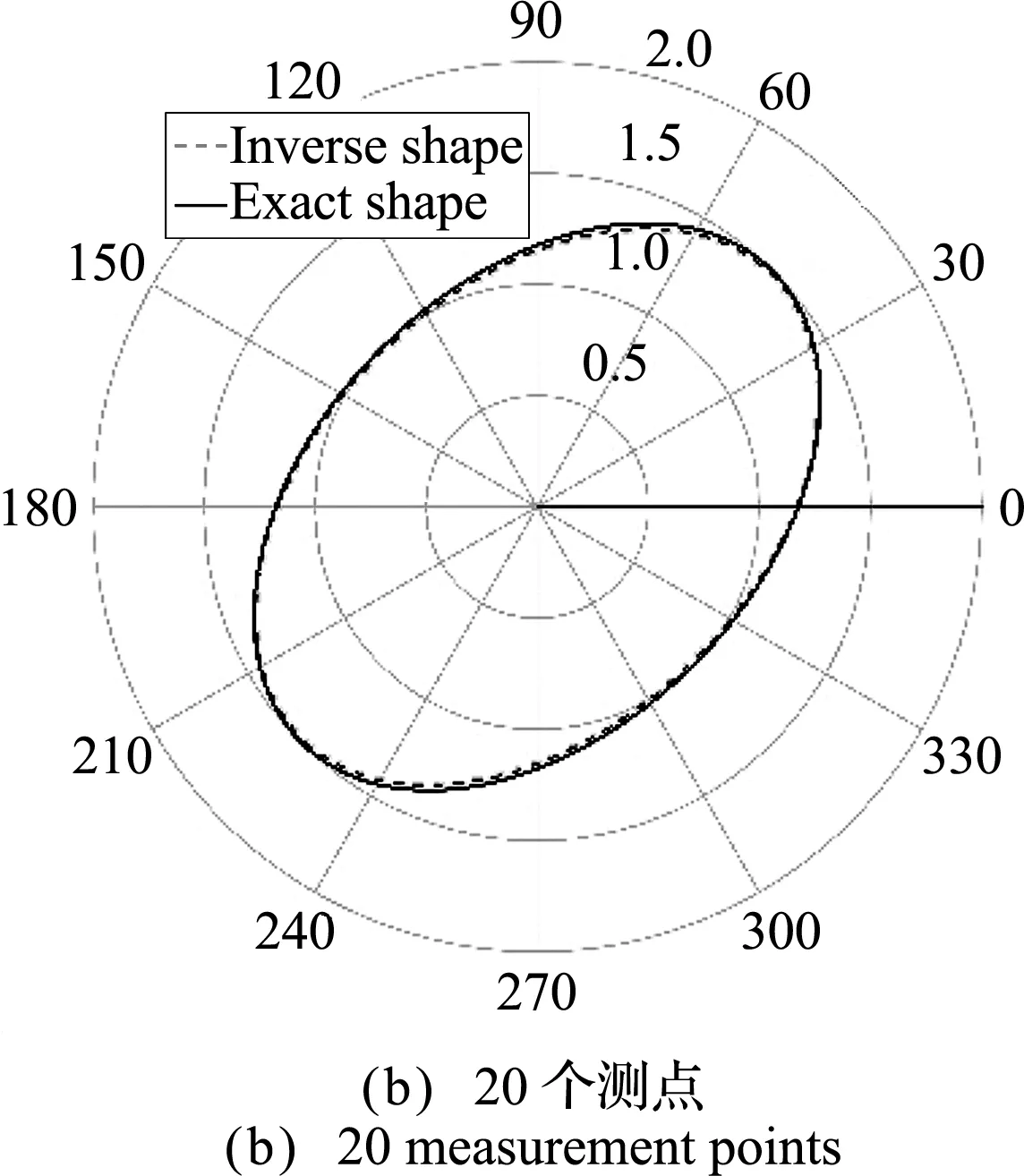
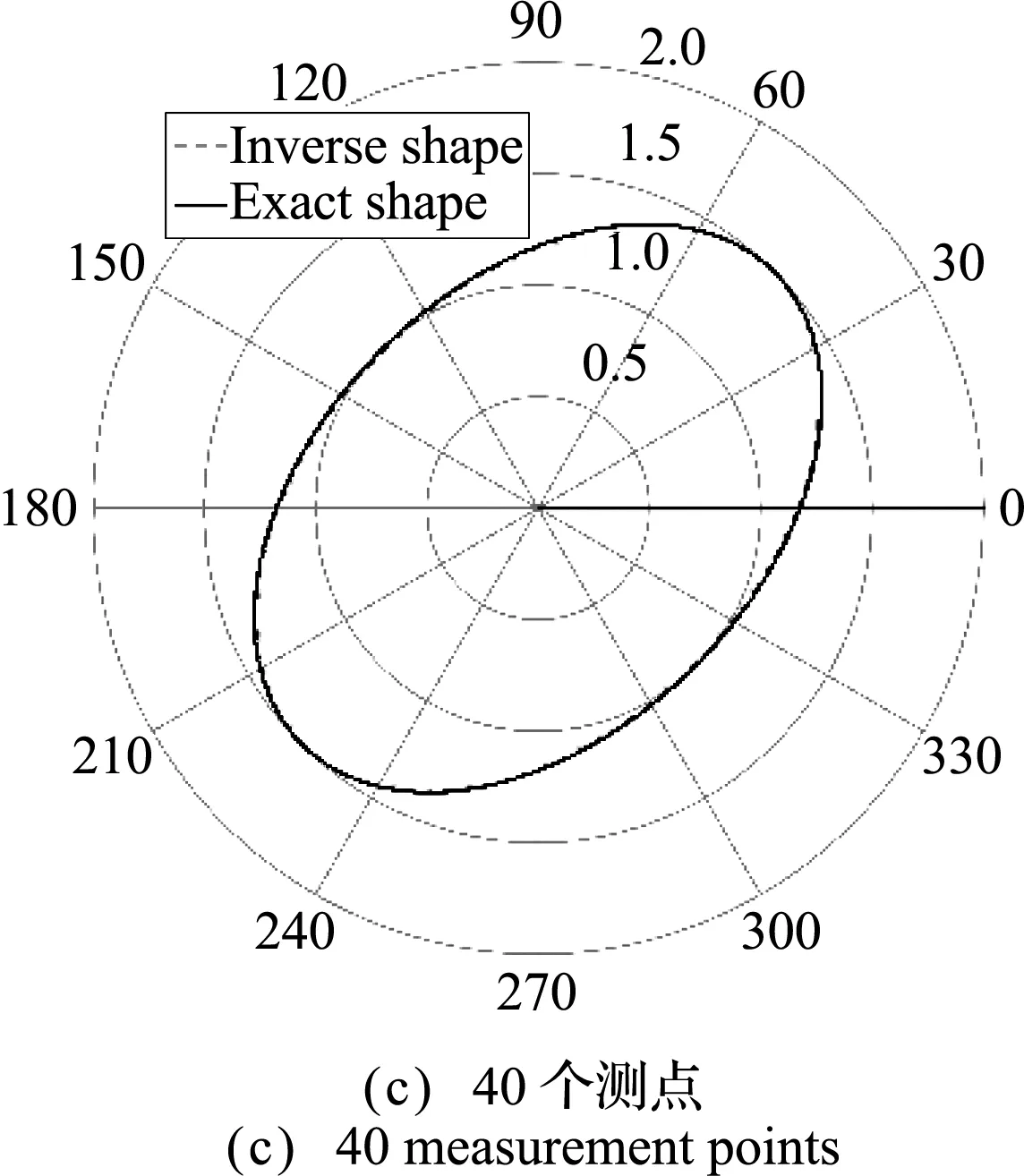
圖11 不同測點數量的反演結果

圖12 不同測點數量時反演結果的相對誤差

3.2 皮膚腫瘤生長參數識別問題

如圖13(a)所示，在笛卡爾坐標系下建立三維皮膚模型，考慮了五種主要的皮膚組織，分別為表皮、乳頭狀真皮、網狀真皮、脂肪和肌肉。假設每一層組織都是有限厚度dm的均勻介質。皮膚組織的有限元模型如圖13(b)所示。皮膚組織的生物熱傳導控制方程可以表示為

圖13 皮膚組織模型

(18)

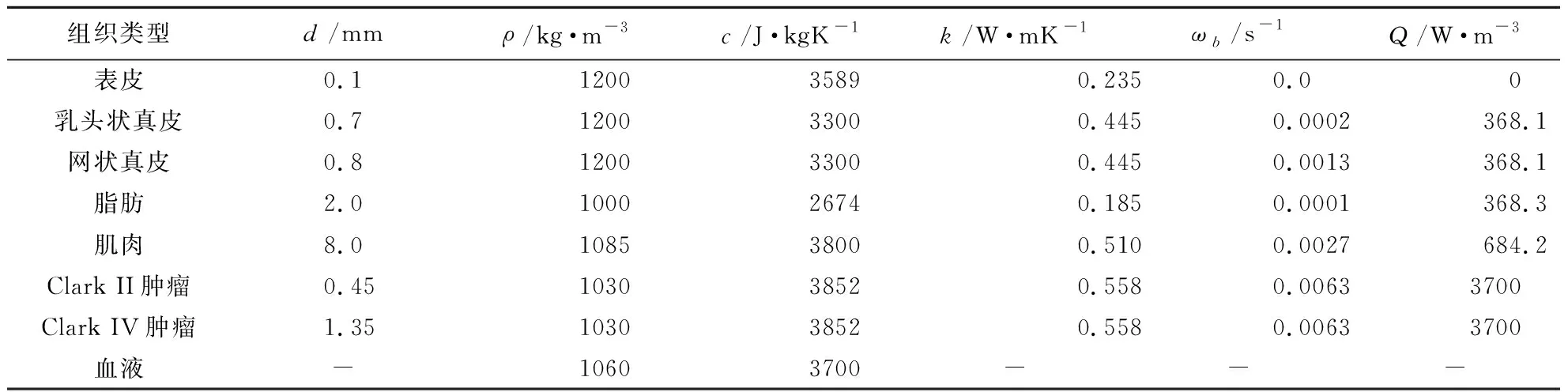
表4 皮膚組織的熱物性參數[5,12]Tab.4 Properties of the skin tissue[5,12]

皮膚腫瘤生長參數識別的深度學習模型如 圖14 所示。首先，將皮膚腫瘤的生長參數形成矩陣；然后利用AE的編碼器部分提取矩陣的抽象特征，利用AE的解碼器部分重構參數矩陣。

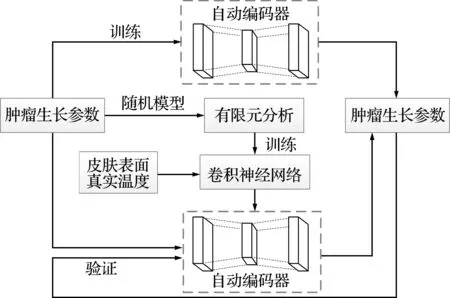
圖14 腫瘤生長參數識別流程

在此基礎上，利用隨機模型，對帶有不同生長參數的有限元模型進行分析，得到了皮膚表面隨時間變化的溫度數據。同時，利用數據訓練CNN，建立皮膚表面溫度與AE特征之間的抽象映射關系。之后，利用真實的皮膚表面溫度，使用已訓練的CNN獲得生長參數的抽象特征。最后，由AE的解碼器部分得到腫瘤的生長參數信息。

本文采用18900個隨機模型作為樣本，同時訓練AE和CNN，分別識別了Clark II和Clark IV腫瘤的生長參數。同時，考慮不同測量誤差對計算結果的影響。表5和表6分別給出了Clark II和Clark IV腫瘤在1%和2%測量誤差下，深度學習模型的識別結果。

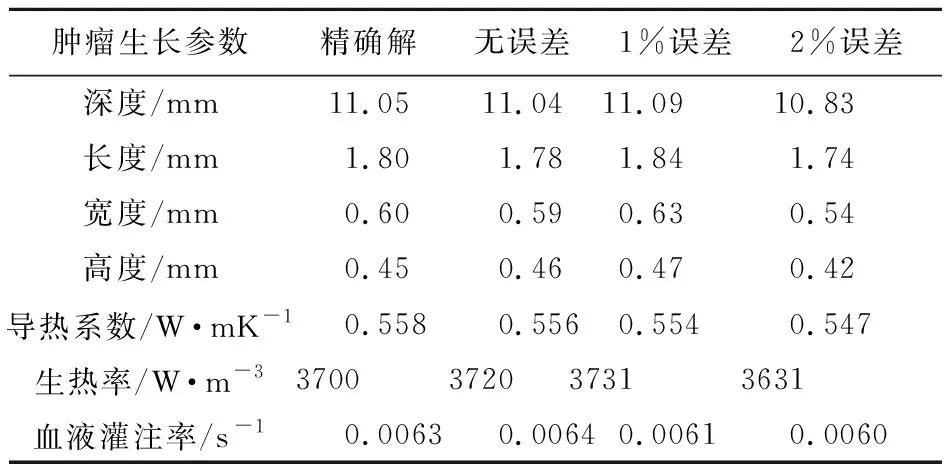
表5 不同測量誤差下的Clark II反演結果

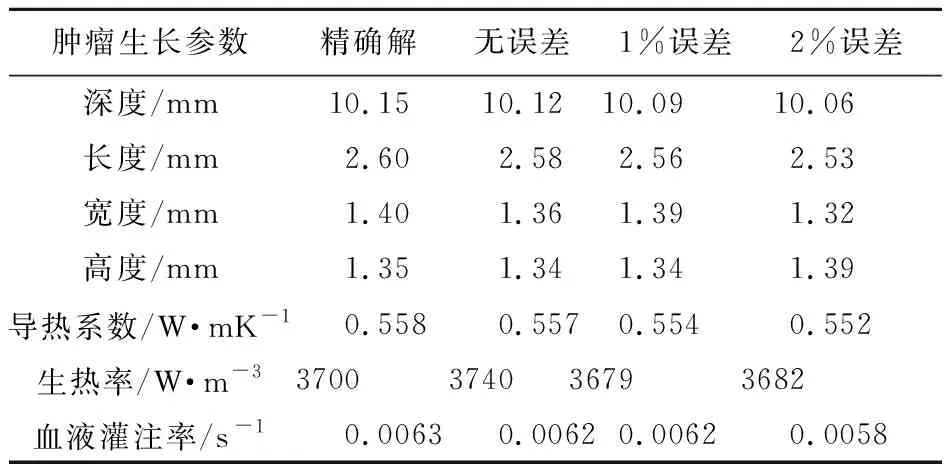
表6 不同測量誤差下的Clark IV反演結果

由表5和表6可知，深度學習模型能夠準確估計腫瘤的生長參數。數值結果表明，皮膚表面的溫度信息包含了腫瘤生長參數的特征。深度學習模型可以提取皮膚表面溫度的抽象特征，建立起生長參數與特征之間的抽象關系。隨著測量誤差的減小，反演結果更加精確。在2%的測量誤差時，仍可以得到較為準確的反演結果。值得注意的是，本文提出的方法能夠準確識別腫瘤的生熱率和血液灌注率，為腫瘤的醫療診斷提供參考。

4 結 論

本文提出了一種基于數據驅動模型求解熱傳導反問題的方法，實現了對導熱管道內壁幾何形狀和皮膚腫瘤生長參數的識別。通過數值算例，對提出的兩個模型進行了驗證，同時討論了不同測量誤差對反演結果的影響。計算結果表明，基于數據驅動模型，能夠有效求解熱傳導反問題。隨著測量誤差的減小，反演結果更加精確。

此外，本文提出的求解模型可以進一步擴展，用于求解其他類型的熱傳導反問題，如導熱系數識別、邊界條件重構以及熱源識別等問題。