組合測試用例生成的向量累加優化算法

宋曉秋，靳龍龍，彭樹敏

(中國航天科工集團第二研究院 七〇六所，北京 100854)

0 引 言

組合測試方法的研究與應用得到了長足的發展[1,2]。近些年，由于實際應用中會伴隨著各種各樣的約束條件，所以帶有約束條件的組合測試用例生成問題越來越受到關注[3-5]。

在武器裝備軟件的系統級測試中，許多測試充分性指標介于兩兩組合[6,7]和三三組合[8,9]之間，即在所有參數滿足兩兩組合覆蓋的基礎上，對其中的關鍵參數附加要求滿足三三組合覆蓋。這是一種特殊的約束條件要求，是在兩兩組合的基礎上附加三三組合的條件，工程中稱之為二三組合。針對這種特殊的混合組合要求，目前還沒有行之有效的成熟算法，需要構造特殊的算法予以解決[10]。

本文采用了一種將組合測試問題轉化為向量累加優化問題的方法，通過向量累加優化問題的求解，反過來得到組合測試問題的解。這種方法使得無論組合測試是何種組合要求，轉化為向量累加優化的問題后，其求解算法都是一樣的，有效地解決了實際工程中組合測試的特殊組合問題。

1 向量累加優化問題

定義1 設Ai=(ai,1,ai,2,…,ai,n)T∈Rn,i=1,2,…,m，滿足：

(1)?i∈{1,2,…,m}，Ai中存在k個1，其余均為0；

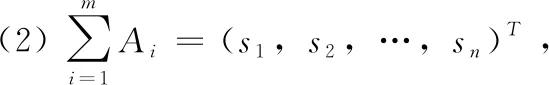
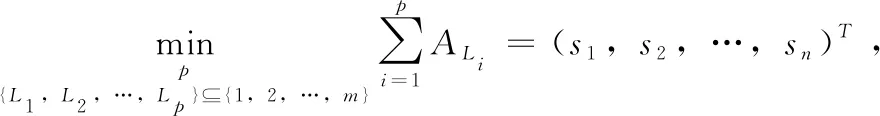
證畢。

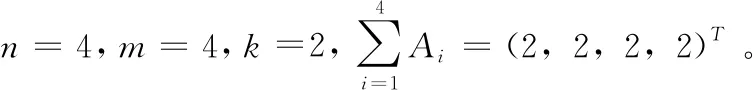
能求解出向量累加優化問題最優解的算法稱為精確算法，無法求解出最優解，但盡量接近最優解的算法稱為近似算法。

2 向量累加優化問題的求解算法

2.1 基本定義

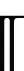
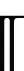
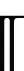
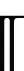
證明：無妨假設B、C和D的元素均是由小到大的排序。

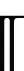
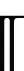
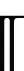
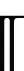
證畢。

2.2 剔除法算法

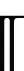
針對向量累加優化問題，初始化Ei=0，i=1,2,…,m(Ei=-1表示剔除Ai，Ei=1表示選中Ai，Ei=0表示Ai待處理)。

記J={j|Ej=0}，J*={j|Ej=-1}，J**={j|Ej=1}。

剔除法算法的步驟為：

步驟1 如果J=φ，則轉步驟4；

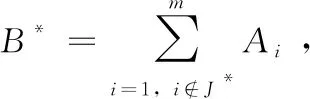
步驟4 輸出解Aj，j∈J**，結束。

該算法經歷一次步驟3，就會減少一個向量，由于是有限個向量，所以步驟4必然會執行到。

2.3 添加法算法

針對向量累加優化問題，初始化S=A1，E1=1，Ei=0，i=2,…,m(Ei=1表示選中Ai，Ei=0表示Ai待處理)。

記J={j|Ej=0}，J*={j|Ej=1}。

添加法算法的步驟為：

步驟1 計算Bj=S+Aj，j∈J；

步驟3 如果S中存在零元素，轉步驟1；

步驟4 輸出解Aj，j∈J*，結束。

該算法經歷一次步驟2，就會添加一個向量，由于是有限個向量，所以步驟4必然會執行到。

2.4 正交法算法

正交法算法是添加法算法的改進，其思路也是從某一個向量開始逐個添加向量，直到所有添加進的向量累積和滿足要求為止，最后所有添加進的向量集即為近似的最優解。為了使添加的向量盡量少，每次選擇與當前向量累加和向量盡可能正交的向量進行添加，這種正交包含了兩種含義，一種是向量的非零位置向量的正交，另一種是向量本身的正交。

定義4 設向量V=(v1,v2,…,vn)T∈Rn，則向量I(V)=(i(v1),i(v2),…,i(vn))T∈Rn稱為向量V的非零位置向量，其中

針對向量累加優化問題，初始化S=A1，E1=1，Ei=0，i=2,…,m(Ei=1表示選中Ai，Ei=0表示Ai待處理)。

記J={j|Ej=0}，J**={j|Ej=1}。

正交法算法的步驟為：

步驟1 計算αj=cos，j∈J；

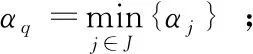
步驟3 記J*={j|αj=αq,j∈J}，計算βj=cos，j∈J*；

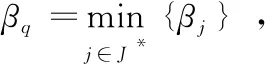
步驟5 如果S中存在零元素，轉步驟1；

步驟6 輸出解Aj，j∈J**，結束。

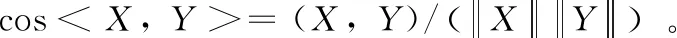
步驟1 計算內積αj=(I(S),I(Aj))，j∈J；

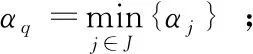
步驟3 記J*={j|αj=αq,j∈J}，計算內積βj=(S,Aj)，j∈J*；

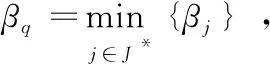
步驟5 如果S中存在零元素，轉步驟1；

步驟6 輸出解Aj，j∈J**，結束。

該算法經歷一次步驟4，就會添加一個向量，由于是有限個向量，所以步驟6必然會執行到。

3 向量累加優化問題在組合測試中的應用

典型的組合測試有：

(1)兩兩組合測試，覆蓋任意兩個參數的所有取值組合。

(2)三三組合測試，覆蓋任意3個參數的所有取值組合。

(3)二三組合測試，覆蓋所有參數的兩兩組合，以及部分參數的三三組合。

設有N個測試用例Ti，i=1,2,…,N，以規定的組合要求為元素，形成測試用例的標識向量Ai。在標識向量Ai中，如果指定的取值組合出現，則對應元素為1，否則為0。由此，組合測試問題轉化為了標識向量Ai的向量累加優化問題。

例3：測試問題2231的測試用例共12個，T1=(1,1,1)T,T2=(1,1,2)T,T3=(1,1,3)T,T4=(1,2,1)T,T5=(1,2,2)T,T6=(1,2,3)T,T7=(2,1,1)T，T8=(2,1,2)T，T9=(2,1,3)T,T10=(2,2,1)T,T11=(2,2,2)T,T12=(2,2,3)T,兩兩組合測試的標識向量設計為

A=(δ(t1:1,t2:1),δ(t1:1,t2:2),

δ(t1:2,t2:1),δ(t1:2,t2:2),

δ(t1:1,t3:1),δ(t1:1,t3:2),δ(t1:1,t3:3),

δ(t1:2,t3:1),δ(t1:2,t3:2),δ(t1:2,t3:3),

δ(t2:1,t3:1),δ(t2:1,t3:2),δ(t2:1,t3:3),

δ(t2:2,t3:1),δ(t2:2,t3:2),δ(t2:2,t3:3))T

∈R16

其中

對應的12個標識向量為

A1=(1,0,0,0,1,0,0,0,0,0,1,0,0,0,0,0)T

A2=(1,0,0,0,0,1,0,0,0,0,0,1,0,0,0,0)T

A3=(1,0,0,0,0,0,1,0,0,0,0,0,1,0,0,0)T

A4=(0,1,0,0,1,0,0,0,0,0,0,0,0,1,0,0)T

A5=(0,1,0,0,0,1,0,0,0,0,0,0,0,0,1,0)T

A6=(0,1,0,0,0,0,1,0,0,0,0,0,0,0,0,1)T

A7=(0,0,1,0,0,0,0,1,0,0,1,0,0,0,0,0)T

A8=(0,0,1,0,0,0,0,0,1,0,0,1,0,0,0,0)T

A9=(0,0,1,0,0,0,0,0,0,1,0,0,1,0,0,0)T

A10=(0,0,0,1,0,0,0,1,0,0,0,0,0,1,0,0)T

A11=(0,0,0,1,0,0,0,0,1,0,0,0,0,0,1,0)T

A12=(0,0,0,1,0,0,0,0,0,1,0,0,0,0,0,1)T

由此，2231的兩兩組合測試問題轉化為了12個標識向量Ai的向量累加優化問題。由剔除法算法求解出的解為{A2,A4,A6,A7,A9,A11}，即T2、T4、T6、T7、T9和T11可滿足兩兩組合覆蓋。

目前有許多兩兩組合算法和三三組合算法，但二三組合算法相對較少。由向量累加優化問題在組合測試中的應用可以看出，無論組合測試中的何種組合要求，一旦轉換為向量累加優化問題，其求解算法是一樣的。所以，向量累加優化問題在組合測試中應用的優勢在于，它能解決諸如二三組合測試這樣的特殊要求的組合測試，當然付出的代價是時間開銷和資源開銷的增加。

4 數值實驗

算法采用C語言編程，計算機主頻2.33 GHz，內存2 GB，操作系統Windows XP。

4.1 兩兩組合測試的數值實驗

為了驗證向量累加優化算法對兩兩組合覆蓋的測試用例優化能力，選取文獻[7]中的28個實驗方案進行實驗。實驗結果見表1，表中的“-”項表示因計算機資源開銷太大或計算時間太長而未得到計算結果。

表1的實驗結果表明：

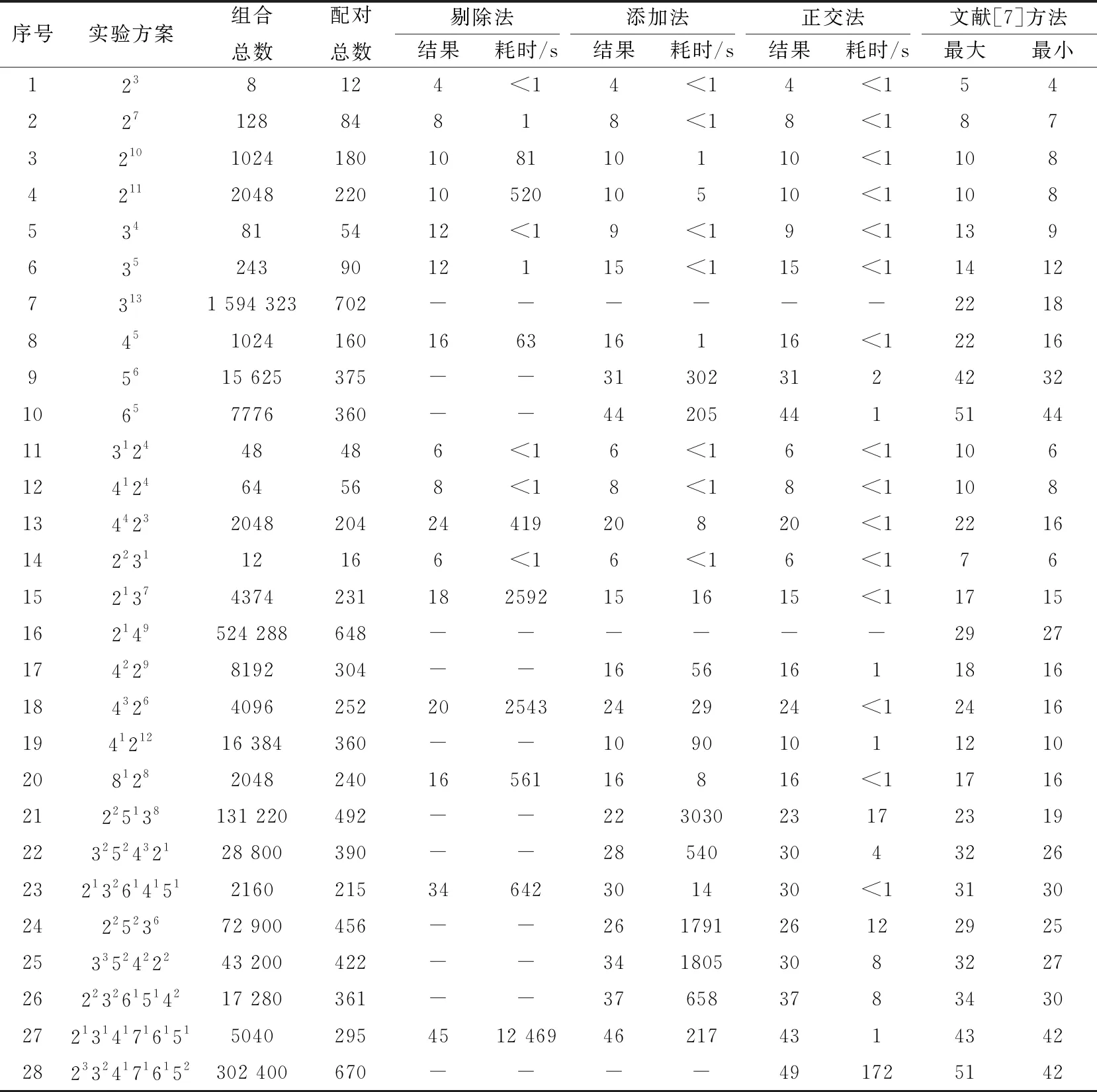
表1 與文獻[7]方法的對比實驗結果

(1)剔除法的計算機資源開銷大、計算時間長，在完成計算的16個實驗結果中，有4個結果比文獻[7]中最差的略差，有6個結果與文獻[7]中最好的一樣，沒有比文獻[7]中最好的更好的。

(2) 添加法的計算機資源和計算時間較剔除法有了很大的改善，在完成計算的25個實驗結果中，有4個結果比文獻[7]中最差的略差，有12個結果與文獻[7]中最好的一樣，有1個結果比文獻[7]中最好的更好。

(3)正交法的計算機資源和計算時間較添加法進一步有了很大的改善，在完成計算的26個實驗結果中，有2個結果比文獻[7]中最差的略差，有12個結果與文獻[7]中最好的一樣，有1個結果(序號9，測試用例集見表2)比文獻[7]中最好的更好。

表2 正交法針對表1中序號9生成的測試用例集

(4)總體上正交法優于添加法，添加法優于剔除法。但序號6和序號18體現了剔除法優于添加法和正交法的結果，序號21和序號22體現了添加法優于正交法的結果。

4.2 三三組合測試的數值實驗

為了驗證向量累加優化算法對三三組合覆蓋的測試用例優化能力，選取文獻[8]中的4個實驗方案進行實驗。實驗結果見表3。實驗結果表明，向量累加優化算法整體上明顯優于文獻[8]中的方法。在表3中，正交法優勢明顯，但針對方案4，剔出法得到了優于其它方法的較好結果。針對方案4，剔除法生成的測試用例集見表4。

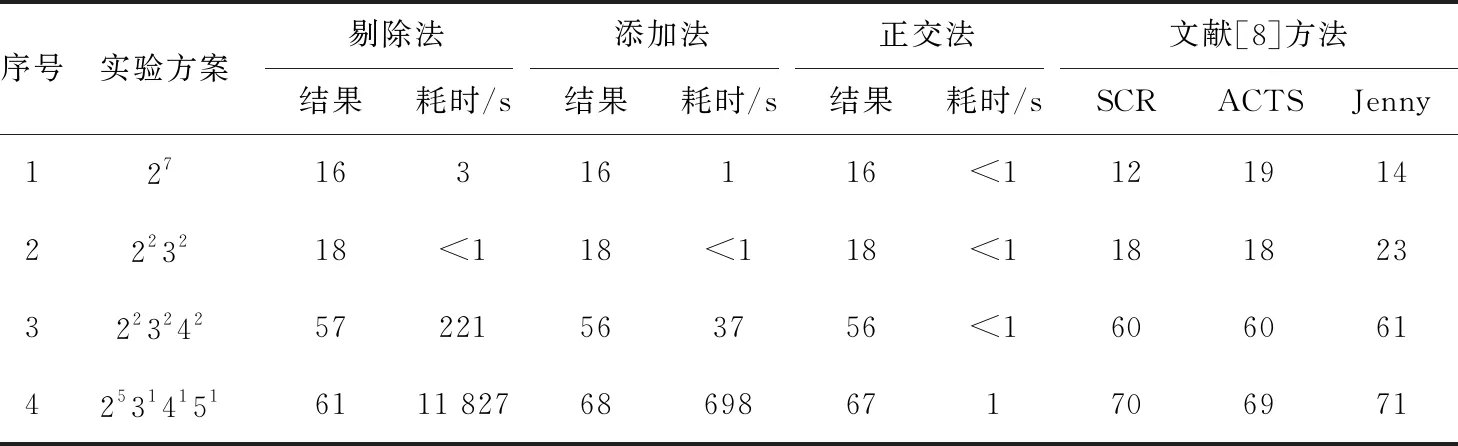
表3 與文獻[8]方法的對比實驗結果

表4 剔除法針對表3中序號4生成的測試用例集

4.3 二三組合測試的數值實驗

為了驗證向量累加優化算法對二三組合覆蓋的測試用例生成的有效性，選取了6個實驗方案進行實驗，實驗結果見表5。在表5中，正交法優勢明顯，但針對方案6，剔出法得到了優于其它方法的較好結果。針對方案1、方案2、方案3，正交法生成的測試用例集見表6。針對方案6，剔除法生成的測試用例集見表7。

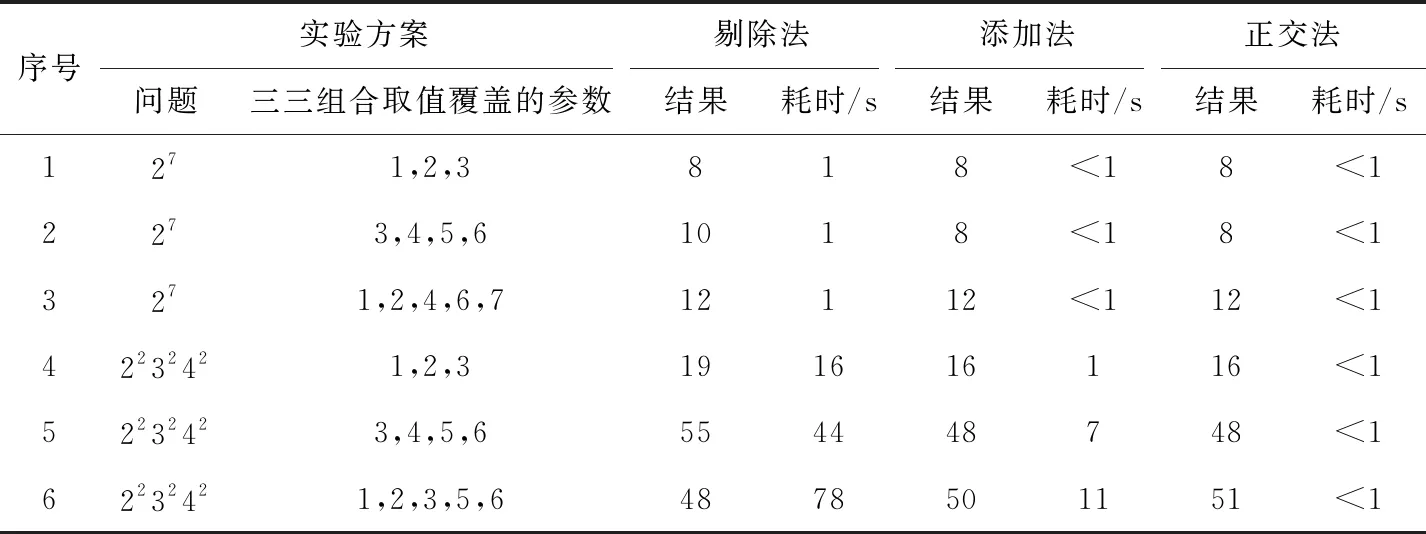
表5 二三組合測試的實驗結果

表6 正交法針對表5中序號1、2、3生成的測試用例集

表7 剔除法針對表5中序號6生成的測試用例集

表5、表6和表7的實驗結果表明：

向量累加優化算法能夠方便有效地生成滿足二三組合覆蓋的測試用例，且優化能力強。

5 結束語

利用向量累加優化算法求解組合測試用例生成問題，其優勢是無論求解何種組合要求的問題，求解算法是一樣的。因此，對于那些特殊組合要求的組合測試問題，向量累加優化算法提供了行之有效的統一的解決方法。向量累加優化算法的劣勢是時間和資源的開銷較大，對規模非常大的組合測試問題就顯得無能為力了。

本文給出的向量累加優化算法并未考慮向量中1值元素的分布特點，今后可以將向量中1值元素的分布特點引入求解算法之中，通過設計針對性的處理步驟，可能會使向量累加優化算法的優化能力得到進一步地提升。未來，通過對向量累加優化算法的進一步研究，有可能得到優化能力更強的新算法，甚至可能針對某類問題得到求解最優解的精確算法。