拉丁方秘密共享方案

李 國，殷俊鋒，李 靜

(中國民航大學 計算機科學與技術學院，天津 300300)

0 引 言

“秘密共享”[1,2]描述了將秘密信息S進行分割，分割后的部分信息稱為一個共享“share”。將share分發給具有保密權限的人員(稱為“參與者”)，每個參與者持有其中的一個share分片，即秘密信息的一部分。部分參與者將持有的share分片結合起來，就能恢復秘密信息S。

拉丁方的數學結構[3]也被用來探究建立秘密共享方案的模型，構建了基于拉丁方特性的秘密共享方案[4-6]。基于拉丁方“臨界集”[7]的秘密共享方案通過分發“臨界集”來實現秘密共享，但找到一個階數n較大的拉丁方臨界集是非常困難的，這使得基于拉丁方臨界集的秘密共享方案初始化和重構難以實現。此外用于秘密共享的拉丁方臨界集直接暴露也使得該類型的秘密共享方案存在缺陷。

針對早前一系列拉丁方秘密共享方案存在的問題，本文提出了一種拉丁方秘密共享方案。該方案利用拉丁方“輪廓與合適的自合痕”可唯一恢復該拉丁方的特性，將隨機生成的部分拉丁方與特殊自合痕構造的拉丁方經過合痕轉換后作為“秘密”，從該秘密拉丁方中隨機選擇“輪廓”，經過合痕轉換后構造門限方案進行秘密共享。對于秘密的重構則需收集一定數量的share分片來進行秘密拉丁方的恢復。本方案初始化階段簡單易操作，在秘密拉丁方的重構階段也簡化了不必要的步驟，同時引入了秘密分片的保護措施，提高了秘密共享的安全性。此外還在秘密共享方案的容錯性和秘密共享的多級方案等方面有所提高。

1 相關知識

1.1 拉丁方

(1)由正整數和0組成的n行n列的方陣，在這個方陣里，恰有n種不同的元素，每一種不同的元素在同一行或同一列里只出現一次。用i,j∈{0,1,2,…,n-1}且n>1分別表示元素k在第i行，第j列的索引。則方陣中任意一個元素k可以用三元組(i,j∶k)來表示。

如圖1所示，左側拉丁陣第2行第1列的元素2可以表示為(2,1∶2)。當i,j∈{1,2,…,n}且n>2時，右側拉丁陣第2行第2列的元素3可以使用(2,2∶3)來表示。

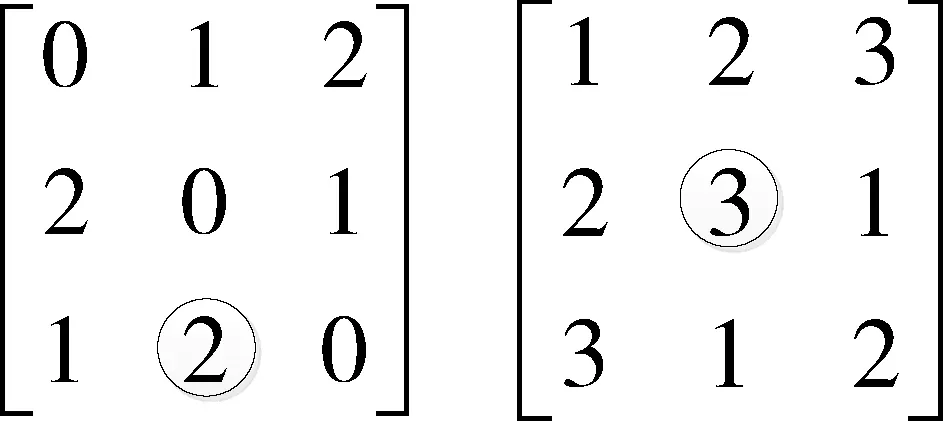
圖1 3階拉丁方

(2)部分拉丁方：設N是n個不同元素的集合，P是一個n階方陣，若N中的每一個元素在P中只出現一次，則稱P是定義在N上的一個部分n階拉丁方，P中有些位置可以為“空”[8]。圖2是在不同位置元素為空的部分3階拉丁方。

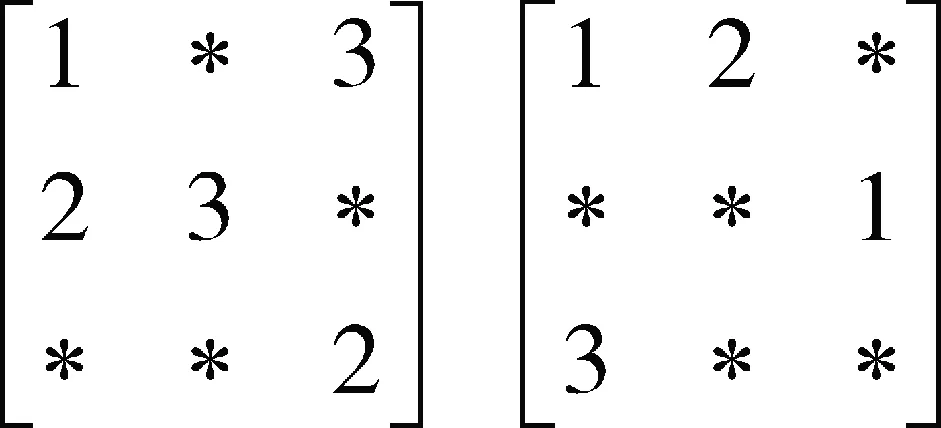
圖2 部分3階拉丁方

1.2 合痕與自合痕

含有n個元素的有限群A的全體置換做成的群，叫作n次對稱群，通常記為Sn。令In=Sn×Sn×Sn，其中Sn是作用于[n]的n次對稱群[9]。對于每一個映射θ=(α,β,γ)∈In。令三元組(i，j∶k)表示拉丁方L中i行，j列的元素k。當三元組通過α交換行的索引，β交換列的索引，γ交換元素符號后得到一個新的拉丁方θ(L)，即：θ(L)=θ((i’,j’∶k’))=(α(i),β(j)∶γ(k))，i，j∈Zn。

則這種映射θ被稱為合痕，經過合痕轉換后的拉丁方θ(L)與拉丁方L是合痕的。而拉丁方L經過映射θ轉換后得到的所有同階拉丁方稱為L的合痕類[10]。

如果θ=(α,β,γ)∈In滿足θ(L)=L，即拉丁方L經過合痕轉換得到該拉丁方L本身，則這種特殊的合痕θ是拉丁方L的一個自合痕，即：L(i，j∶k)=θ(L)=θ((i’，j’∶k’))=(α(i),β(j)∶γ(k))，i，j∈Zn。

1.3 輪 廓

在拉丁方L中挑選部分三元組集合構成一個部分拉丁方P，在一個合適的自合痕θ作用下經過循環置換可以重構拉丁方L，則稱這個部分拉丁方P為“輪廓”，使用“C”來表示[11]。

算法1： 輪廓C與合適的自合痕θ生成拉丁方L。

輸入： 輪廓C， 自合痕θ

輸出： 拉丁方L

(1)L ← n×n arrays

(2) for i← 0 to n-1

(3) for j← 0 to n-1

(4) if(C[i][j]≠null)

(5) for k∈{0,1,…,n-1}

(6) L[i][j]←θk(C[i][j])

(7) endfor

(8) endif

(9) endfor

(10) endfor

(11) return L

例如：當自合痕θ=((012),(012),(012))的時候，使用算法1從輪廓C經過循環置換可以得到拉丁方陣L。圖3是(C,θ)生成拉丁方L的具體過程[12]。

圖3 輪廓C與合適的自合痕θ生成拉丁方L

2 拉丁方秘密共享方案

2.1 方案初始化步驟

利用拉丁方“輪廓與合適的自合痕”可唯一恢復該拉丁方的特性，將隨機生成的部分拉丁方P與特殊自合痕ξ構造的先導拉丁方Lpre經過合痕轉換后生成的拉丁方L作為“秘密S”，從該秘密拉丁方L中選擇部分三元組得到輪廓C與合適的自合痕θ，隨后將經過合痕轉換后的C’中的三元組集合進行隨機分割，得到的碎片稱為“share”。由唯一具有分發授權的參與者將share分片隨機分發給其它N個參與者δ1,δ2,…,δN。 δ持有的部分信息作為秘密拉丁方的共享“share”。該拉丁方秘密共享方案主要有以下4步：

步驟1 在特殊自合痕ξ下生成先導拉丁方Lpre。隨機構造一個n階部分拉丁方P。令i∈{0，1，…，n/2-1}，隨機選擇ki∈{0，n/2}。得到P的三元組集合A[12]，即：A={(n/2-1-i,i∶ki)，(n-1-i，n/2+i∶ki)，(n-1-i,i∶n/2-ki)，(n/2-1-i，n/2+i∶n/2-ki).}以n=6為例，從三元組集合A中得到部分拉丁方P

令特殊自合痕ξ=(τ,τ,τ)，τ=(0,1,…,n/2-1)(n/2,n/2+1,…,n-1)。定理1和算法1保證了(P,ξ)生成拉丁方Lpre。當n=6時，ξ=((012)(345),(012)(345),(012)(345))，部分拉丁方P與特殊自合痕ξ可以得到秘密拉丁方L的先導拉丁方Lpre

定理1 令D=(di,j)是一個部分n階拉丁方陣，其中包含2n個已經定義的元素，每個元素都屬于{0，n/2}。當且僅當：

(1)每個塊M11、M12、M21和M22都精確地包含n/2個元素；

(2)如果(i,j,di,j)和(i’,j’,d’i,j)是一個塊中的兩個不同的項，那么j-j’≡i-i’(mod n/2)

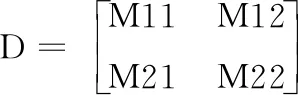
然后，(D,ξ)生成一個拉丁方。(特別注意的是定理1必須保證在n≡2(mod4)情況下成立。)

證明：這是一個定理的特殊情況[13]。

步驟2 隨機生成秘密拉丁方L與自合痕θ；

隨機生成一個合痕Φ，令L=Φ(Lpre)，將拉丁方L作為秘密S。根據引理1可知：由Lpre的特殊自合痕ξ=(τ,τ,τ)與合痕Φ進行運算，可以得到L=Φ(Lpre)的自合痕θ=ΦξΦ-1。例如：隨機生成Φ=((15234),(134),(1243))，則秘密拉丁方L

由引理1可知，Lpre的特殊自合痕ξ與合痕Φ和Φ-1經過循環置換得到L=Φ(Lpre)的自合痕θ=ΦξΦ-1=((053)(124),(032)(154),(024)(135))。

引理1令λ∈S3。令θ、Φ∈In，并且L是一個n階拉丁方。然后：

(1)當且僅當ΦξΦ-1∈Atp(Φ(L))時，θ∈Atp(L)；

(2)當且僅當θλ∈Atp(Lλ)時，θ∈Atp(L)。

引理1的證明在文獻[14]。

步驟3 利用秘密拉丁方L的輪廓C得到C’；

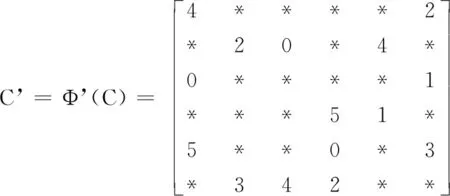
在拉丁方L中選擇m∈(n2/3≤m≤n2/2且N取整數)個三元組得到輪廓C，再隨機生成合痕Φ’，令C’=Φ’(C)。利用C’包含的三元組構造(K，N)門限秘密共享方案。

例如在L中挑選15個三元組組成輪廓C，隨機生成合痕Φ’=((145),(14352),(1423))

將輪廓C包含的三元組在合痕Φ’下進行合痕轉換得到C’

由于輪廓C是秘密拉丁方L的一部分，將C直接分發給參與者后每個參與者就得到了秘密拉丁方L的一部分信息，相當于直接暴露了秘密S的一部分，一個不懷好意的攻擊者極有可能利用這些裸露的share分片進行攻擊從而得到整個秘密拉丁方L。為了避免這一情況的發生，進行上述操作，經過合痕轉換后的C’不包含秘密拉丁方L的任何信息，避免了在之前的拉丁方秘密共享方案中share分片等重要信息的直接暴露，增加了秘密拉丁方L的安全性，防止部分秘密分片的泄露危害整個秘密的安全，進而保證了秘密S的足夠安全。

步驟4 將C’進行隨機分發；

根據(K,N)門限秘密共享方案[15]的要求由具有安全權限的分發者將C’隨機分發給N個參與者(K值可以根據實際情況的要求進行隨機選擇)，得到δ1-δN的三元組集合，每個參與者得到的share分片所包含的信息量是相同的。

例如在K=4，N=5時構造(4，5)門限秘密共享方案，將C’分為5份：δ1-δ5，每個δ中包含了3個三元組集合，每一份的詳細構造如下

δ1=((0，0∶5)，(3，0∶0)，(4，2∶2)), δ2=((1，0∶3)，(3，3∶4)，(2，5∶5)), δ3=((1，3∶1)，(4，5∶0)，(2，4∶2)), δ4=((1，4∶0)，(4，1∶5)，(2，2∶1)), δ5=((5，4∶3)，(0，3∶2)，(5，1∶4)).

在早期的拉丁方秘密共享方案中，含有秘密的share分片不能丟失，不能損毀，缺少任何一個share分片就不能進行秘密的恢復。基于此，本文中在秘密分發過程中利用門限秘密共享方案增加了早前拉丁方秘密共享方案所沒有的“容錯性”，K個或者多于K個share分片結合在一起就能夠恢復秘密拉丁方L。因此本方案可以容忍一定數量的share分片丟失或損毀，剩余的share分片同樣能夠恢復秘密拉丁方L。

對于前文構造的(4，5)門限秘密共享方案來說：任意得到δ1-δ5中的4個share分片，就可以利用本文中的拉丁方秘密共享方案的恢復過程解得秘密拉丁方L，進而得到秘密S。該拉丁方秘密共享方案的“容錯性”極大減少了秘密丟失的風險，有力提高了秘密保護的安全性。

經過拉丁方秘密共享方案的初始化步驟后，每個參與者可以得到C’的一部分信息share分片，自合痕θ與合痕Φ’是公開的。但這種公開是有條件的，為了秘密的足夠安全，不會把θ與Φ’公開給所有人，只會將它們公開給具有權限的參與者。換句話說，本方案選擇將θ、Φ’與C’一起分發給參與者。圖4描述了該拉丁方秘密共享方案的初始化流程。(PRNG是偽隨機數發生器)。

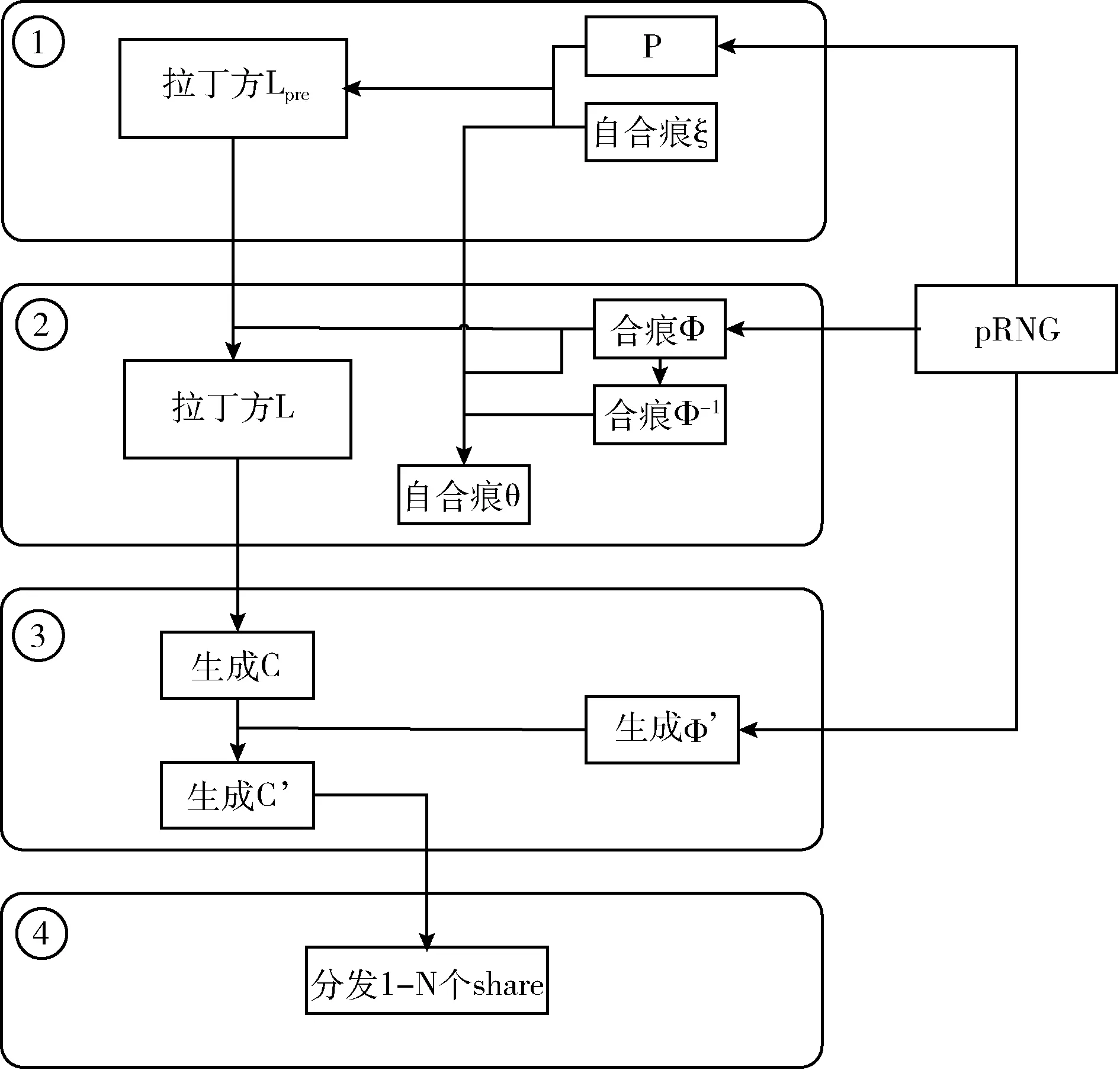
圖4 方案初始化流程

2.2 秘密拉丁方L的重構

秘密拉丁方L的重構是初始化的逆過程，首先收集部分參與者持有的“share”分片結合組成C’，由隨機合痕Φ’經過運算得到Φ’-1。C’與Φ’-1經過循環置換的逆過程得到輪廓C，C與自合痕θ利用算法1恢復秘密拉丁方L，進而得到秘密S。方案的主要過程有以下兩步：

步驟1 根據(K,N)門限秘密共享方案的要求，任意收集K到N個參與者持有的share分片組合起來得到C’，同時得到自合痕θ與合痕Φ’，將合痕Φ’求逆得到Φ’-1

θ=((053)(124),(032)(154),(024)(135))， Φ’-1=((541),(25341),(3241))；

C’與Φ’-1經過循環置換的逆過程得到輪廓C

步驟2 將輪廓C中的元素使用三元組表示，與自合痕θ結合，使用算法1根據拉丁方的定義經過循環置換后就能夠重構秘密拉丁方L，得到秘密S。以下是輪廓C中的三元組集合通過自合痕θ進行循環置換的詳細步驟

通過上述的運算可以得到秘密拉丁方L各個位置元素的三元組集合，因此就能重構秘密拉丁方L，得到秘密S

在之前的秘密共享方案中，一個很重要的問題就是無法保證收集share分片的正確性，由此恢復的秘密正確性受到質疑。在本文秘密拉丁方的重構過程中，如果得到的輪廓C與自合痕θ不能重構拉丁方L，證明收集的share分片出現了錯誤，需要重新收集正確的share分片。換句話說，拉丁方L具有“自檢測性”。這個特性避免了使用錯誤的share分片去重構拉丁方L，并且對于恢復秘密的正確性也有足夠的保證。圖5描述了秘密拉丁方L重構S的流程。

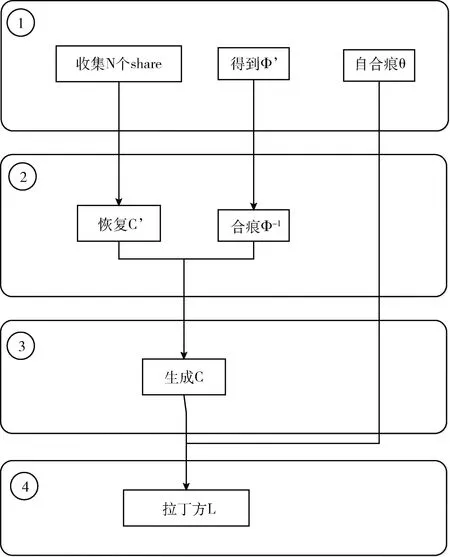
圖5 方案重構流程

2.3 分片泄露后的秘密保護措施

以往的拉丁方秘密共享方案中沒有考慮秘密分片泄露后如何進行秘密的恢復保護。例如一個參與者不小心把自己持有的share分片泄露出去，某些不懷好意的攻擊者極有可能利用這些泄露的share分片進行攻擊從而得到需要保護的秘密。為了秘密的安全，需要將這些有可能泄露的秘密進行替代或者使用新的方法再次進行加密，這個過程是非常耗費時間以及其它資源的。能否在share分片泄露后丟棄這些具有潛在泄密風險的share分片，同時進行share分片的更新，使用新的share分片來進行秘密共享，在不更換秘密的情況下盡最大可能進行秘密的保護是值得考慮的。

本文的拉丁方秘密共享方案可以有效解決這一問題，假如部分share分片由于某些未知原因丟失或者泄露，為了保護秘密的安全，可以實行以下“分片泄露后的秘密保護措施”，對本方案進行如下的改進：

(1)即對于泄露的分片，同樣將它們收集起來，運行秘密拉丁方L重構過程的第一步：利用門限秘密共享方案將δ1-δN收集起來組成C’，運行恢復過程C=Φ’-1(C’)得到輪廓C，將失去作用的C’和Φ’丟棄。

(2)重新生成一個隨機合痕Φ’，重復初始化過程的第3、4步，再將輪廓C使用Φ’進行合痕轉換生成新的C’，對C’構造門限秘密共享方案進行重新分發。

例如：假若由于某些原因載有秘密信息的share分片泄露，先采取措施(1)，通過拉丁方重構過程中的第一步得到輪廓C

再采取措施(2)，重新生成一個新的合痕Φ’=((2543),(13245),(254)，得到新的C’

得到C’后通過初始化階段的步驟4進行秘密分片的重新分發。對于秘密拉丁方L的恢復則通過拉丁方的重構過程。使用分片泄露后的秘密保護措施，無需修改輪廓C，也不用更新秘密拉丁方L就能得到新的share分片，避免了秘密分片泄露帶來的安全隱患。如果分片沒有泄露，也可以進行分片的定期更新，處于動態變化中的share分片有力提高了秘密共享方案的安全性。

本文中拉丁方秘密共享方案的一個潛在的重要應用是將秘密拉丁方L作為加密密鑰，share分片的更新措施可以用于加密密鑰的保護。通過該拉丁方秘密共享方案將密鑰分片進行分發，若部分密鑰分片泄露或者丟失，可以將泄露的密鑰分片進行丟棄、更新操作。通過該方案，可以在不改變加密密鑰的情況下進行密鑰分片的更新，避免了密鑰更新帶來的重新解碼加密數據、生成新的加密密鑰、再進行重新加密的巨大工作量，有力保護了密鑰與加密數據的安全，節約了大量的時間資源。

3 方案分析

3.1 安全性分析

(1)暴力攻擊

攻擊者可能會使用大量的計算資源通過系統的組合秘密的所有可能性，直到得到秘密。對于拉丁方秘密共享方案來說，為得到秘密拉丁方L，攻擊者會使用暴力攻擊手段對一個n階拉丁方的所有可能排列進行一一遍歷，直到得到所需要的秘密拉丁方L。盡管在理論上存在這種可能性，但是在實際情況下一個n階拉丁方的合痕類數量是非常巨大的。例如一個n階拉丁方陣，第1行有n!種填充方式，對于第2行第1列，有n-1個數字可以填充，第2行第2個數字有n-2種填充方式，以此類推：拉丁陣第2行一共有(n-1)!種填充方式。第3行有(n-2)!種,…,第n行有2!種。因此對于一個n階拉丁方陣，符合要求的拉丁方陣數量是：n!(n-1)!(n-2)!…2!。以下是階數n在8到12的拉丁方及其合痕類的數量

n=8:數量：108,776,032,459,082,956,800； n=9:數量：9!×8!×7!×6!×5!×4!×3!×2!； n=10:數量：10!×9!×8!×7!×6!×5!×…×2!；

n=11:數量：11!×10!×9!×8!×7!×6!×5!×…×2!；

n=12:數量：12!×11!×10!×9!×8!× 7!×6!×5!×…×2!；

根據現有的知識，得到階數n較大的拉丁方的全部可能排列是非常困難的，因此在數量如此巨大的拉丁方中通過使用暴力攻擊的方式對n階拉丁方的全部可能排列進行一一遍歷，進而來找到秘密拉丁方是幾乎“不可能”的。因此可以認為該拉丁方秘密共享方案是足夠安全的，可以有效抵御攻擊者的暴力破解攻擊。

(2)部分參與者的背叛

對于(K,N)門限秘密共享方案來說由K個或多于K個參與者所持有的share分片上的信息可以重構秘密S，而少于K個參與者持有的share分片就無法得到秘密S。

本文中的拉丁方秘密共享方案中使用了門限秘密共享方案進行share分片的分發，因此如果其中一部分參與者共同發生背叛行為，將自身持有的share分片結合起來，對秘密拉丁方L進行恢復，這在理論上是可行的，但必須要求有K個或者K個以上的參與者共同背叛才能達到這種效果，少于K個參與者持有的share分片上的信息無法進行秘密拉丁方L的重構，即不可能得到秘密拉丁方L。例如拉丁方秘密共享方案中在share分片分發階段構造的(4,5)門限方案中，只有4個及4個以上的參與者共同背叛，它們持有的share集合所包含的信息才能夠得到輪廓C，而少于4個的share組合并不能得到秘密拉丁方L。因此在拉丁方秘密共享方案中部分share分片信息的泄露不會影響秘密拉丁方L的安全，但為了避免這種潛在的風險，要求在選擇參與者的時候應盡量避免這種大規模參與者背叛情況的發生，從而保證秘密的絕對安全。

(3)C’丟失

在循環結構(n/2)(n/2)下，n次對成群Sn中的可能的置換數量是“n!(2!(n/2)2)=2(n-1)!/n”。因此，n階拉丁方L的合痕類數量可以表示為“(2(n-1)!/n)3”。n階拉丁方L的自合痕θ的集合用“Atp(L)”表示，通過“軌道-穩定集”定理，n階拉丁方L的合痕類數量也可以表示為“is(L)=n!3/Atp(L)”[16]。

在已知n的情況下，表1給出了n階拉丁方中合適的合痕、自合痕等數據。

表1 n階拉丁方合痕、自合痕的數量

假設在某種情況下，共享的share全部丟失，被不法的攻擊者獲得，攻擊者利用這些share分片得到了C’。為獲得秘密拉丁方L，攻擊者必須還要得到合痕Φ’與自合痕θ，從合痕類中猜測Φ’的正確則的概率是1/is(L)，由表1可知：即使是在n=10的情況下這種可能性也是非常小的。這樣就很難從C’中得到正確的輪廓C，因此通過暴力攻擊手段得到輪廓C是不可能的。即使在某種可能性很小的情況下攻擊者得到了Φ’，進而得到了輪廓C，但是沒有自合痕θ的參與恢復拉丁方L同樣是不可能的，這樣的秘密保護機制被稱為“雙重防護”。此外，還可以對自合痕θ和合痕Φ’進行切割后隨機的分發給參與者，沒有二者的參與同樣不能恢復秘密，進一步提升安全性。

3.2 秘密共享方案的多級方案

在信息系統中很多有重要價值的信息往往需要進行加密來保護信息的安全，信息的使用者需要在密鑰的配合下對密文進行解密操作才能獲得想要的信息。對于加密后的重要數據，不懷好意的攻擊者需要使用一切手段獲得加密密鑰，一旦密鑰丟失，密文就會有極大的概率丟失，因此對于加密密鑰的保護是信息系統的重中之重。為了保證密鑰的絕對安全，需要將密鑰分發給具有不同權限級別的參與者。只有不同權限級別的參與者共同分享自己持有的子密鑰時才能得到原始密鑰，換句話說，任何一個參與者僅僅通過自身持有的子密鑰并不能得到唯一的密鑰，因此秘密共享方案在密鑰保護方面也有潛在的應用。

使用本文中的拉丁方秘密共享方案，可以構造安全性更高的秘密保護的多級方案。如圖6所示，秘密拉丁方L作為一個密鑰K，恢復L需要3部分數據的協助，包括“C’，θ和Φ’”。拉丁方秘密共享方案將C’進行分發，對于θ，Φ’來說，是公開的(但這種公開是有條件的，僅僅向獲得權限的參與者公開，無權限人員并不能得到該數據)。在秘密共享的多級方案中，放棄這種公開，并且規定了兩種級別的權限：高級權限P1與普通權限P2。P1所持有的share分片重要性高于P2。隨后將自合痕θ與Φ’分發給P1級的參與者，C’分發給P2級別的參與者。只有P2級的參與者結合生成的C’與P1級的參與者持有的自合痕θ與Φ’相結合，才能恢復秘密拉丁方L，進而得到密鑰K。3個條件缺少其中的任何一個，均不能得到密鑰K，這極大提高了密鑰K的安全性，同時為拉丁方在秘密共享的多級方案應用提供了可能。

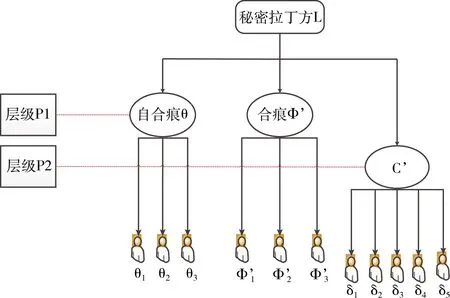
圖6 秘密共享的多級方案

4 結束語

本文提出了一種拉丁方秘密共享方案，利用拉丁方的輪廓與合適自合痕可唯一恢復該拉丁方的特性，將具有自合痕轉換性質的拉丁方作為“秘密”，將合痕轉換后的輪廓進行秘密共享。本方案使得拉丁方秘密共享方案的初始化和秘密重構簡單易行，同時減少了秘密共享過程中數據的規模，避免了秘密分片的直接暴露，增加了秘密的安全性。隨機選擇輪廓中三元組的數量構造(k,N)門限秘密共享方案，為秘密提供了足夠的冗余來提高方案的容錯性，解決了早前拉丁方秘密共享方案任何一個秘密分片丟失后秘密就會完全丟失的問題。同時該方案還在秘密共享的多級方案、秘密分片泄露保護等方面進行了推廣。

本文的拉丁方秘密共享方案僅僅考慮了在n=2(mod 4)的情況下，未來的一個研究方向是將n進一步推廣到任意的正整數值。另外秘密共享方案共同的不足在于返回過程中識別哪些share是不正確的，在該方案中，錯誤的share組成的輪廓在恢復階段是不能得到唯一拉丁方的，但這個驗證發生在了恢復的最后階段，能否在share收集階段驗證其正確性也是值得思考的。