具有指數(shù)衰減振蕩型概率密度變化規(guī)律的產品壽命分布模型

劉永明，趙帥帥，趙轉哲，陳 玉，趙宏偉

（1.安徽工程大學機械與汽車工程學院，蕪湖241000；2.安徽師范大學物理與電子信息學院，蕪湖241000）

壽命分布是描述機械產品和電子產品失效數(shù)據(jù)的分布規(guī)律和可靠性的重要方法，在壽命數(shù)據(jù)分析、可靠性設計、疲勞可靠性分析、維修決策、保修策略制定等方面得到了廣泛的應用[1?2]。壽命分布決策的準確性直接影響到產品可靠性分析、使用壽命評定、風險評估、維修決策制定等效果。

目前關于機械產品壽命分布的研究主要以Weibull等[3?4]開發(fā)的三參數(shù)威布爾分布模型為主，該模型可以描述早期故障、偶發(fā)故障和耗損性故障，適用于復雜設備故障分布，在可靠性領域得到廣泛的應用。多年來，國內外學者從不同角度對三參數(shù)威布爾模型進行了研究[5?12]。Cordeiro等[5]提出了一種新的指數(shù)威布爾分布模型，并研究了該模型的概率密度函數(shù)和失效率函數(shù)。Wang等[6]提出了一種基于核主成分分析和威布爾比例風險模型的滾動軸承可靠性評估方法，減小了可靠性評估中同一類型軸承在制造、安裝、工作條件等方面的差異。Freels等[7]提出兩參數(shù)威布爾分布的幾種修改方式，用于分析“浴盆”型壽命分布。Baloui[8]基于模糊威布爾和組件壽命，建立了模糊可靠性函數(shù)。南東雷等[9]提出使用蒙特卡洛方法結合極大似然估計法對三參數(shù)威布爾分布模型進行參數(shù)點估計數(shù)值求解。位林營等[10]提出了基于指數(shù)威布爾分布的復雜電子系統(tǒng)使用可靠度建模方法，可動態(tài)描述系統(tǒng)可靠度變化。

然而，并不是所有的機械產品壽命分布曲線都具有威布爾分布的形狀特征，工程實際中復雜產品的很多故障是具有周期性和振蕩型的，其壽命分布因會呈現(xiàn)出衰減振蕩的變化規(guī)律，即隨著使用時間的增加產品的壽命分布概率密度總體呈指數(shù)衰減，局部振蕩的變化趨勢。而目前國內外對威布爾模型的研究大多是忽略了機械產品的周期性故障引起的概率密度的振蕩問題，這往往與實際的工程數(shù)據(jù)存在一定的誤差，影響了模型應用的精度。

本文在傳統(tǒng)壽命分布模型的基礎上，構建具有指數(shù)衰減振蕩概率密度分布規(guī)律的壽命分布模型，給出相應的可靠度、失效率以及平均壽命計算模型。在此基礎上，研究衰減系數(shù)、振蕩幅值、振蕩角頻率等參數(shù)對概率分布特征的影響，最后以某型叉車搭載的液力自動變速箱故障時間數(shù)據(jù)為研究對象，運用建立的概率分布模型對該型液力自動變速箱故障時間數(shù)據(jù)進行擬合，并與指數(shù)分布模型、三參數(shù)威布爾模型和“浴盆曲線”模型擬合結果進行對比，驗證所建立的概率分布模型的有效性。

1 指數(shù)衰減振蕩型概率密度分布模型構建

當產品失效率曲線具有振蕩型特征的時候，其概率密度具有指數(shù)衰減振蕩的特征。可以構建如式（1）所示的三參數(shù)產品壽命概率分布模型，其概率密度函數(shù)為

式中：t為壽命度量指標，且t≥0；λ為衰減系數(shù)；A為振蕩幅值；ω為振蕩角頻率。

由式（1）所示的壽命概率密度函數(shù)可以推導出產品的壽命累積分布函數(shù)為

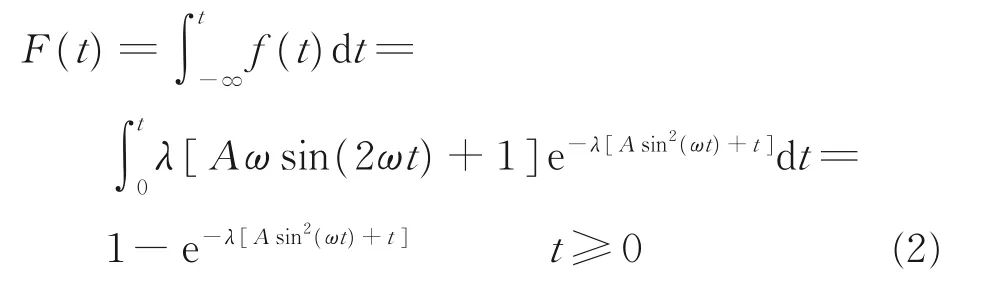
顯然式（1）滿足如下條件，即

同時，式（2）能夠滿足以下完備性要求，即

因此，式（1）可以作為壽命分布的概率密度函數(shù)，式（2）可以作為壽命分布的累積分布函數(shù)，式（1，2）可以作為指數(shù)衰減振蕩型壽命分布模型。

進一步，根據(jù)可靠度與壽命累積分布函數(shù)之間的關系，可以推導出可靠度的表達式為

失效率函數(shù)的表達式為

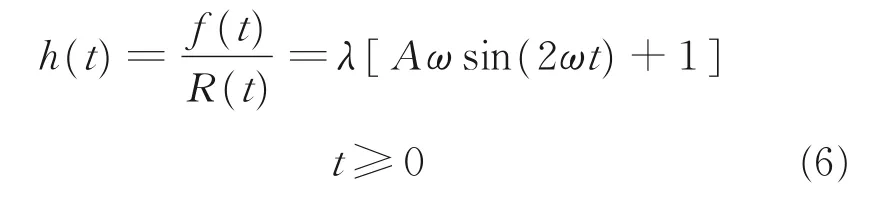
平均壽命計算模型的表達式為

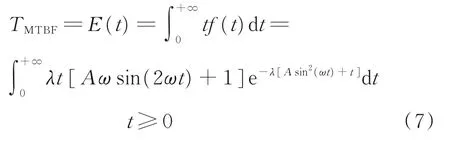
2 不同參數(shù)對壽命概率分布特征的影響

針對式（1）所示的概率分布模型，分別研究衰減系數(shù)λ，振蕩幅值A，振蕩角頻率ω等對壽命概率分布特征的影響規(guī)律。

2.1 衰減系數(shù)對壽命概率分布特征的影響

當A=100，ω=0.001，λ分 別 為0.000 2、0.000 5、0.000 8時，所對應的概率密度曲線、可靠度變化曲線和失效率變化曲線分別如圖1～3所示。

圖1 衰減系數(shù)對概率密度的影響Fig.1 Effect of attenuation coefficient on probability density

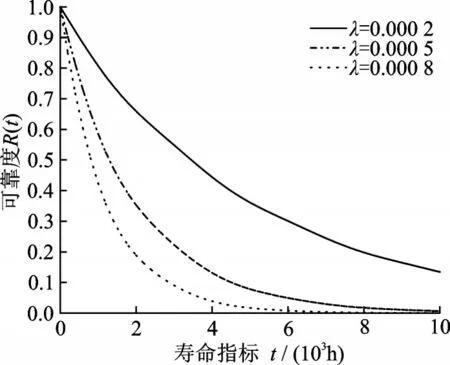
圖2 衰減系數(shù)對可靠度的影響Fig.2 Effect of attenuation coefficient on reliability

由圖1～3可以看出，衰減系數(shù)λ越小，失效率越低，可靠度越高，概率密度變化越平緩。同時，由圖1可以看出，概率密度呈指數(shù)衰減振蕩變化規(guī)律，由圖3可以看出，失效率不在是一恒定不變的常數(shù)，具有一定的周期性和波動性，且波動周期一樣。

圖3 衰減系數(shù)對失效率的影響Fig.3 Effect of attenuation coefficient on failure rate

2.2 振蕩幅值對壽命概率分布特征的影響

當λ=0.000 2，ω=0.001，A分別為200、500、800時，所對應的概率密度曲線、可靠度變化曲線和失效率變化曲線分別如圖4～6所示。

圖4 振蕩幅值對概率密度的影響Fig.4 Effect of oscillation amplitude on probability density

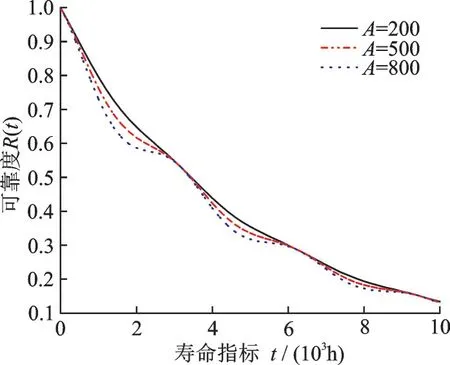
圖5 振蕩幅值對可靠度的影響Fig.5 Effect of oscillation amplitude on reliability

由圖4～6可以看出，振蕩幅值A越大，概率密度、可靠度及失效率振蕩越劇烈。同時，由圖4可以看出，概率密度呈指數(shù)衰減振蕩變化規(guī)律，由圖6可以看出，失效率不在是一恒定不變的常數(shù)，具有一定的周期性和波動性，且波動周期一樣。

圖6 振蕩幅值對失效率的影響Fig.6 Effect of oscillation amplitude on failure rate

2.3 振蕩角頻率對壽命概率分布特征的影響

當λ=0.000 2，A=500，ω分 別 為0.000 2、0.000 4、0.000 6時，所對應的概率密度曲線、可靠度變化曲線和失效率變化曲線分別如圖7～9所示。

圖7 振蕩角頻率對概率密度的影響Fig.7 Effect of oscillation angular frequency on probabili?ty density

圖8 振蕩角頻率對可靠度的影響Fig.8 Effect of oscillating angular frequency on reliability

由圖7～9可以看出，振蕩角頻率ω越大，概率密度、可靠度及失效率振蕩越快。同時，由圖7可以看出，概率密度呈指數(shù)衰減振蕩變化規(guī)律，由圖9可以看出，失效率不在是一恒定不變的常數(shù)，具有一定的周期性和波動性，且ω越大，波動周期越小。

圖9 振蕩角頻率對失效率的影響Fig.9 Effect of oscillation angular frequency on failure rate

3 指數(shù)衰減振蕩型壽命分布模型的應用

為驗證所建模型的實用性，以某型號叉車為例，該型號叉車2018年售出3萬輛，跟蹤一年售后維修記錄，其搭載的液力自動變速箱117臺發(fā)生故障，儀表盤記錄的部分故障時間按升序排列如表1所示。

表1 液力自動變速箱部分故障時間Table 1 Partial failure time of automatic transmission

采用經(jīng)驗分布的方法，計算該液力變速箱故障時間的概率密度分布曲線、可靠度曲線及失效率曲線，如圖10～12所示。

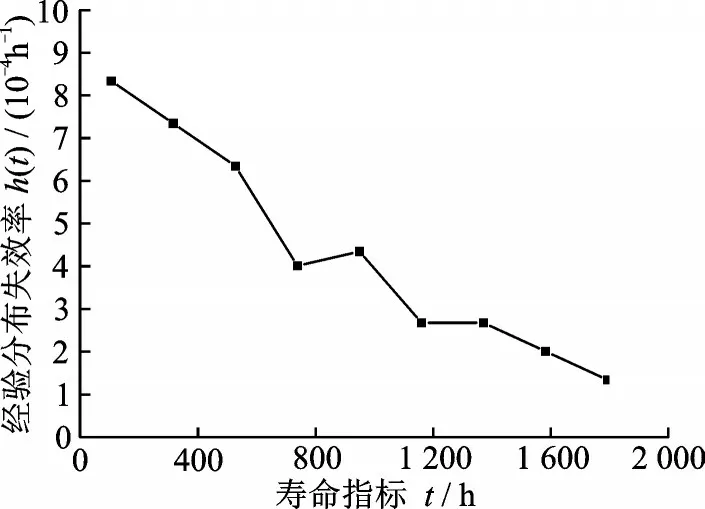
圖10 經(jīng)驗分布概率密度Fig.10 Probability density of empirical distribution

圖11 經(jīng)驗分布可靠度Fig.11 Reliability of empirical distribution

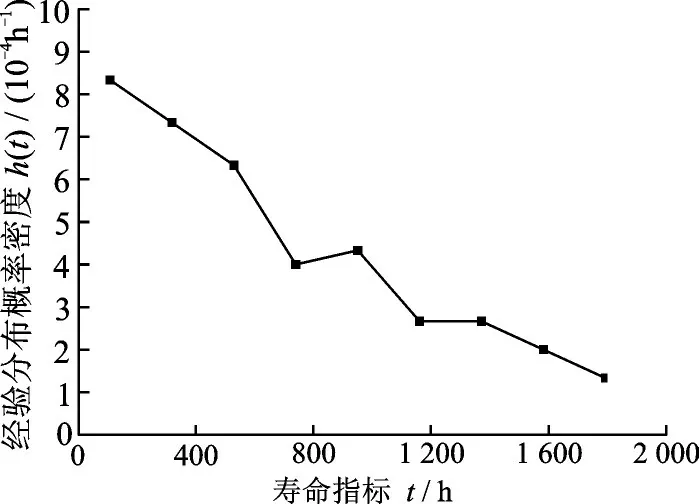
圖12 經(jīng)驗分布失效率Fig.12 Failure rate of empirical distribution

從圖10～12可以看出，該液力自動變速箱的壽命概率密度、可靠度及失效率隨時間增加呈現(xiàn)出衰減振蕩的變化特征。顯然，該液力自動變速箱的概率密度分布特征不易采用傳統(tǒng)的指數(shù)分布、正態(tài)分布、兩參數(shù)威布爾分布和三參數(shù)威布爾分布等概率密度模型描述。基于該液力自動變速箱在若干時刻點的故障數(shù)據(jù)（表1），計算壽命概率密度值，在此基礎上利用式（1）對其壽命概率密度特征進行參數(shù)擬合，并與采用指數(shù)分布、三參數(shù)威布爾及文獻[13]所提“浴盆曲線”模型擬合結果進行對比，結果如圖13所示，4種方法擬合結果的均方根誤差如表2所示。

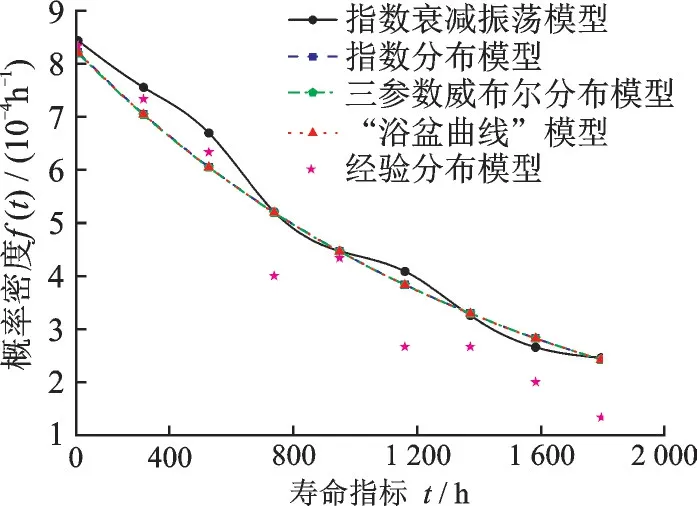
圖13 概率密度對比Fig.13 Comparison of probability density

表2 均方根誤差對比Table 2 Comparison of root mean square error

由圖13及表2可以看出，與指數(shù)分布、三參數(shù)威布爾分布和文獻[13]所提“浴盆曲線”模型相比，在擬合曲線形狀上，所建立的指數(shù)衰減振蕩模型能夠較好地模擬該液力自動變速箱無故障工作時間概率密度在t為528.28、739.32、950.35、1 161.38和1 372.42 h的衰減振蕩特征。這是因為，在衰減振蕩模型中指數(shù)部分通過引入周期函數(shù)，更好地描述了數(shù)據(jù)的振蕩特性，同時，從表2中可以看出，采用指數(shù)衰減振蕩模型可以獲得較小的擬合均方根誤差。

采用式（1）所示的概率密度模型，計算得到該液力自動變速箱的無故障工作時間概率密度擬合模型為

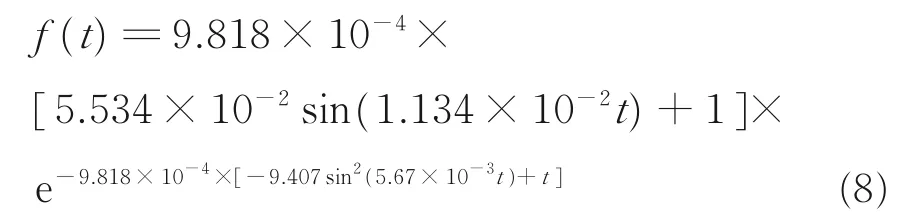
進一步可求得可靠度和失效率模型分別為

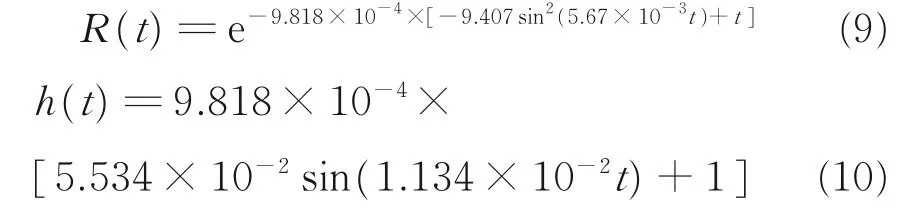
4 結 論

（1）在指數(shù)累計失效分布模型的基礎上，通過引入具有振蕩特征的周期函數(shù)Asin2(ωt)，構建指數(shù)衰減振蕩分布的可靠性模型，并推導了相應的概率密度、可靠度、失效率以及平均壽命計算模型。

（2）在此基礎上，研究衰減系數(shù)、振蕩幅值、振蕩角頻率等參數(shù)對概率分布特征的影響。總體上，概率密度呈指數(shù)衰減振蕩變化規(guī)律，失效率不再是一恒定不變的常數(shù)，具有一定的周期性和波動性。其中衰減系數(shù)λ越小，失效率越小，可靠度越高，概率密度變化越平緩；振蕩幅值A越大，概率密度，可靠度及失效率振蕩越劇烈；振蕩角頻率ω越大，概率密度，可靠度及失效率振蕩越快。

（3）對某型叉車搭載的液力自動變速箱的故障時間數(shù)據(jù)進行其壽命密度和失效率分析，其經(jīng)驗分布概率密度和失效率具有衰減振蕩的特征，運用建立的指數(shù)衰減振蕩概率密度模型對其壽命概率密度特征進行參數(shù)擬合，并與指數(shù)分布、三參數(shù)威布爾分布和文獻[13]所建立的“浴盆曲線”模型擬合結果進行對比。對比結果顯示，所建立的指數(shù)衰減振蕩模型能夠較好的模擬該液力自動變速箱無故障工作時間概率密度的衰減振蕩特征，采用指數(shù)衰減振蕩模型可以獲得較小的擬合均方根誤差，其擬合均方根誤差為3.677e-005。