吸氣式高超聲速飛行器預設反演魯棒控制

王鵬飛，羅 暢，劉承君，張 峰，章 華

(1 陸軍炮兵防空兵學院，合肥 230031；2 78092部隊，成都 610000)

0 引言

吸氣式高超聲速飛行器(air-breathing hypersonic vehicles，AHV)是一類以超燃沖壓發動機為動力，可在20～100 km空間范圍內以速度大于5Ma遠距離飛行的新型飛行器[1-3]。但是，由于AHV具備諸多與傳統低空慢速飛行器顯著不同的動力學特征，使得其控制系統的設計十分困難。美國研制的X-43A高超聲速驗證機首次試驗就因控制系統無法滿足預設軌跡跟蹤要求而失敗。因此，設計滿足性能要求的控制系統對我國AHV的發展十分關鍵。

目前，已有多種控制方法應用于高超聲速飛行器的控制器設計，如增益調度控制[4]、反饋線性化控制[5]、滑模控制[6]和反演控制[7-9]等。其中，反演控制方法由于對嚴格反饋非線性系統具有良好的處理能力，因而已成為AHV主流的控制設計方法。文獻[10]在反演控制的框架下，引入自適應滑模控制提升魯棒性；文獻[11]基于微分器設計干擾觀測器來補償模型中的不確定項；文獻[8]和[12]分別將模糊控制、神經網絡控制與反演控制相結合，有效提高了魯棒性。

上述研究基本只考慮閉環系統的穩定性，而對控制器的瞬態性能如超調量和調節時間等指標未做約束。基于文獻[13]和[14]提出的預設性能控制方法，文中提出一種預設性能反演魯棒控制方法，實現對飛行器控制系統的瞬態性能約束。通過引入預設性能函數對速度和高度系統的跟蹤誤差進行轉換，從而實現對誤差瞬態性能的約束和調整。為提升反演控制的魯棒性，基于改進的反正切微分器[15]構造一種新型干擾觀測器對飛行器模型中的不確定項進行估計。同時，為避免“計算膨脹”問題，引入滑模微分器獲取高度子系統中各虛擬導數的估計。最后，通過仿真實驗，驗證所設計的控制系統能夠實現對其瞬態性能的約束。

1 問題描述

1.1 動力學建模

AHV的彈性動力學模型[16]為：

(1)

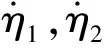
1.2 預設性能

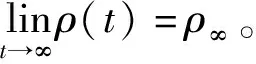
根據文獻[17]，預設性能函數可選取為:

ρ(t)=(ρ0-ρ∞)e-lt+ρ∞

(2)

式中：ρ0和ρ∞分別是ρ(t)的初值和終值；l為待設計的正參數。

根據預設性能的定義，系統誤差e(t)應滿足:

(3)

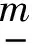
(4)

其中ε(t)為S[ε(t)]的逆函數。則系統誤差可表示為:

e(t)=ρ(t)S[ε(t)]

(5)

反解式(4)可得ε(t)為：

(6)

對式(6)求導得：

(7)

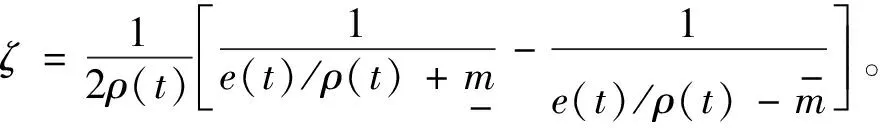
2 控制器設計

根據時間刻度原理[18]，可將AHV動力學模型拆分為速度系統與高度系統分別設計控制器。

2.1 速度控制器

根據式(1)可將速度子系統轉換為:

(8)

式中：fV和gV是包含氣動力和氣動參數的函數；dV為包含彈性擾動的未知項。

(9)

由式(6)設計速度的轉換誤差εV(t)為

(10)

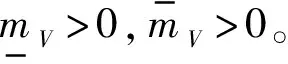
對式(10)求導得：

(11)

基于動態逆理論，設計速度控制系統的輸入Φ為:

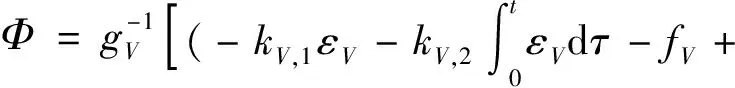
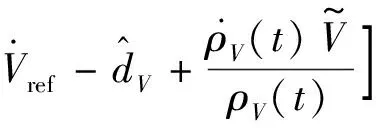
(12)

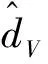
2.2 高度控制器

根據式(1)將高度子系統轉換為:

(13)

式中：fγ，gγ，fQ及gQ均是包含氣動力和氣動參數的函數，dγ與dQ為包含彈性擾動的未知項。

(14)

高度的轉換誤差εh(t)可表示為：

(15)

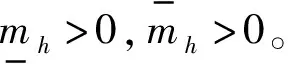
對式(15)求導得:

(16)

選取虛擬控制律γc為:

(17)

式中，kh,1>0和kh,2>0,均為設計參數。

為避免“計算膨脹”，這里引入滑模微分器[19]對γc估計：

(18)

式中，λ11和λ12為待設計參數。

(19)

令虛擬控制量θc為:

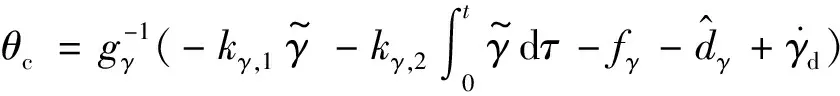
(20)

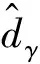
類似的，對θc的一階導數估計可得:

(21)

式中，λ21和λ22為待設計參數。

(22)

定義虛擬控制量Qc為:

(23)

式中，kθ,1與kθ,2均為大于0的參數。

同樣，對Qc的導數估計可得:

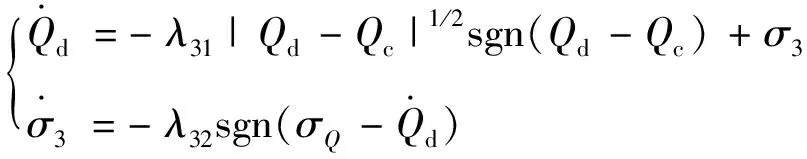
(24)

式中，λ31與λ32為待設計的正參數。定義高度子系統中3個虛擬控制量一階導數的估計誤差為ex=xd-xc,(x=γ,θ,Q)，根據文獻[19]可知選擇合適參數能保證ex有界，即一定存在大于零的常數ei,M,能夠使|ex|≤ex,M,(x=γ,θ,Q)。

(25)

選取高度子系統的實際輸入δec為:

(26)

式中，kQ,1和kQ,2為控制器參數。

2.3 干擾觀測器設計

為降低模型中不確定項對控制效果的影響，提升反演控制的魯棒性，基于MATDs[15]構造一種新的非線性干擾觀測器對不確定項估計：

(27)

式中:x=V,γ,Q；Rx、bx、lx,1和lx,2均為待設計的正參數。

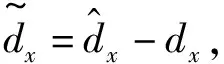
2.4 穩定性分析

選擇Lyapunov函數為:

W=WV+Wh+Wγ+Wθ+WQ

(28)

其中

對式(28)求導得:

(29)

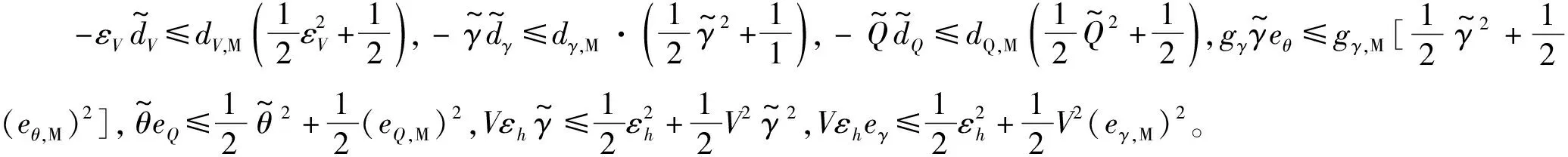
因此可得：

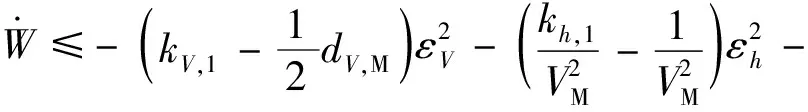
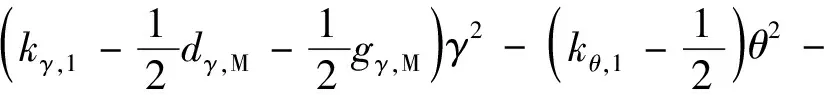
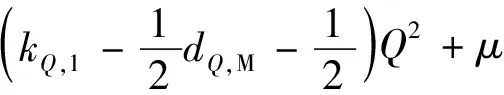
(30)

其中

(31)

(32)

(33)

(34)

(35)

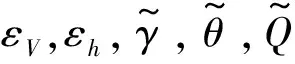
3 仿真實驗

基于設計的控制器進行速度和高度參考指令的跟蹤仿真，飛行器模型中的所有數據參見文獻[16]。控制器參數取kV,1=2,kV,2=15,kh,1=12,kh,2=1,kγ,1=0.3,kγ,2=0.2,kθ,1=0.9,kθ,2=0.2,kQ,1=0.6,kQ,2=0.1;滑模微分器的取值：λ11=λ21=λ31=0.0949,λ12=λ22=λ32=0.0015; 干擾觀測器的取值：Rx=5，bx=0.9，lx,1=14和lx,2=15，其中x=V,γ,Q。選取預設性能函數的形式為：

(36)

設定AHV的初始速度V=2346.96 m/s,初始高度h=25908 m。速度參考的階躍信號為ΔV=500 m/s，高度跟蹤的信號為Δh=1000 m。為了驗證控制器的魯棒性，在仿真100～200 s之間，令模型中所有氣動參數在±20%之間按正弦規律攝動。此外，在同等條件下將文中算法與文獻[11]的方法進行對比，驗證所設計控制器的優越性。

仿真結果如圖1～圖5所示。從圖1和圖2可以看出，速度和高度的跟蹤誤差很好地被限制在了預先設定的范圍之內。當氣動參數發生攝動時，跟蹤誤差的微小變化不會對飛行器的飛行姿態造成影響。此外，相比文獻[11]的結果，文中設計的控制器無論是在控制性能還是魯棒性方面均有一定的優勢。圖3為控制輸入，可以看到除了在仿真初期有短暫的抖振，整體較為平滑。圖4和圖5顯示飛行器所有的剛體和彈性體狀態量能夠迅速達到穩定，在存在參數攝動時也能保持在較小范圍內變化。

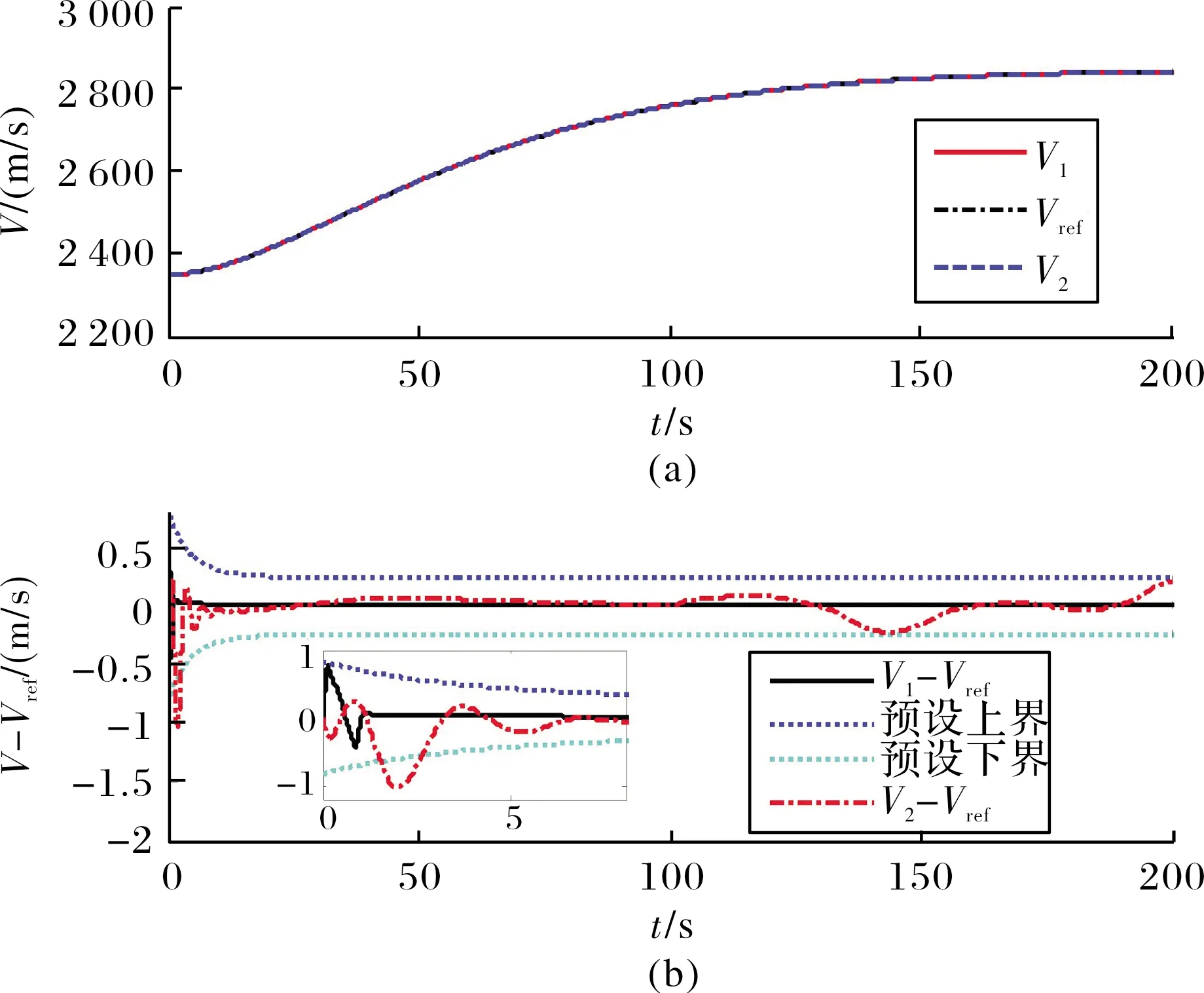
圖1 速度及其跟蹤誤差

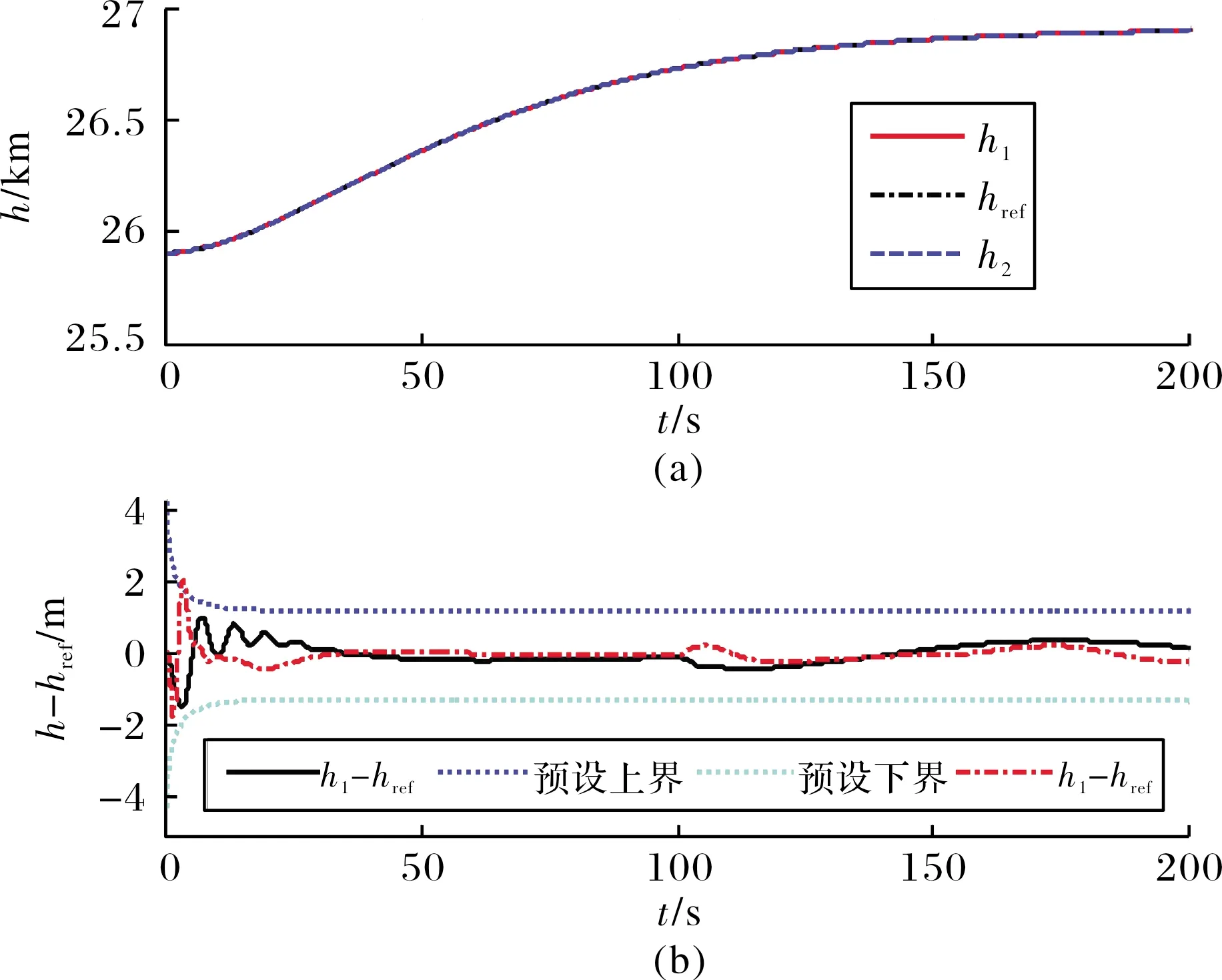
圖2 高度及其跟蹤誤差

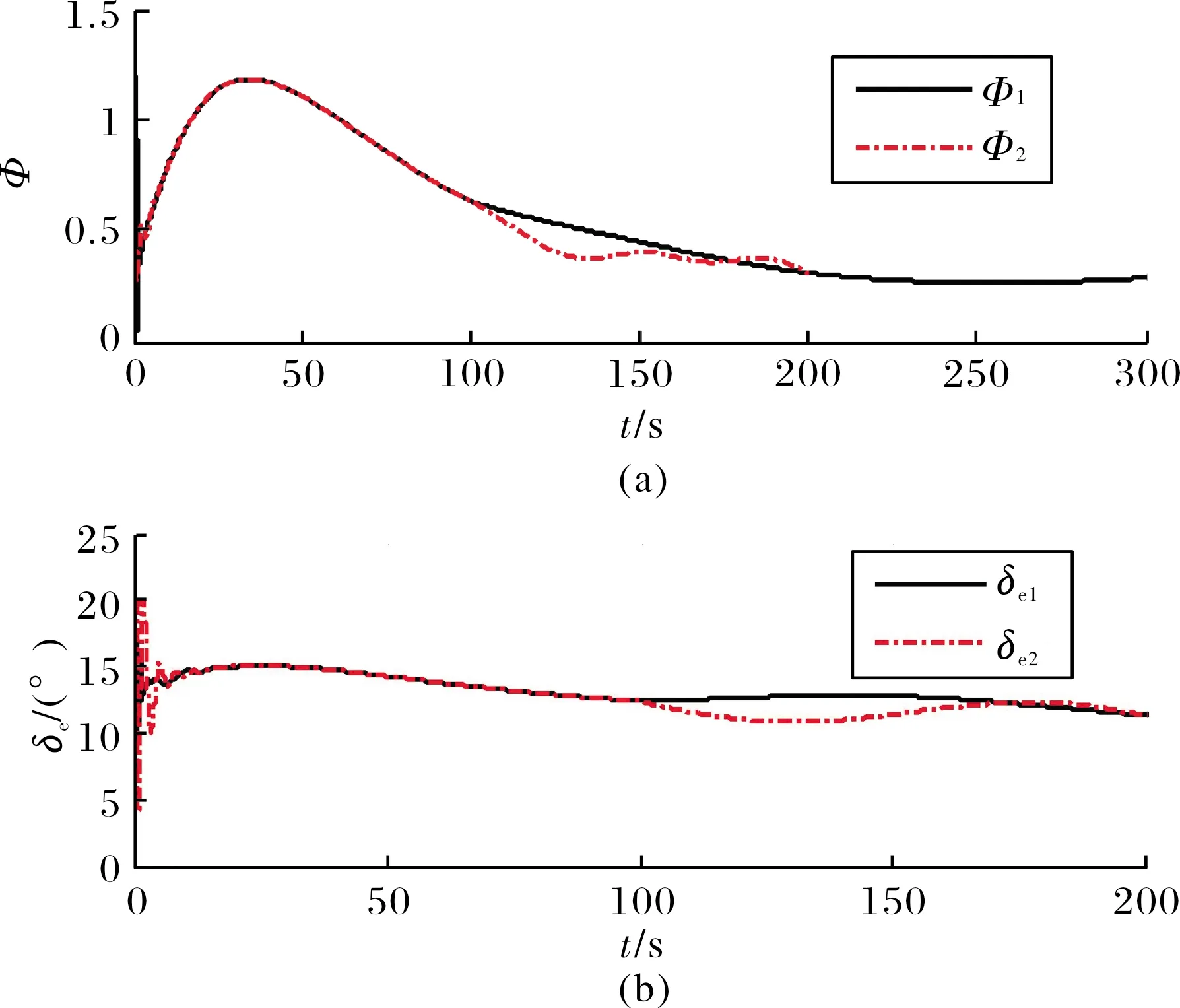
圖3 控制輸入

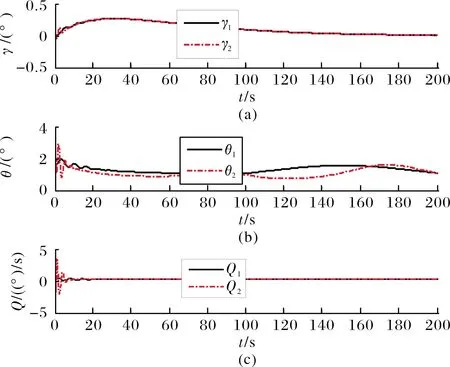
圖4 航跡角，俯仰角及俯仰角速率

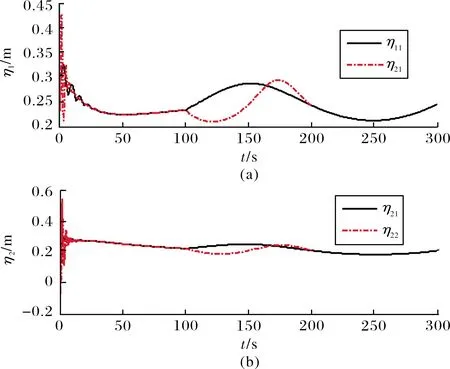
圖5 彈性狀態

4 結論

設計了一種預設反演魯棒控制器，能夠實現對控制系統跟蹤誤差瞬態性能的約束。為改善單純反演控制魯棒性不高的問題，引入了基于MATDs構造的干擾觀測器。通過跟蹤軌跡的對比仿真實驗可以發現，該控制器具有良好的控制性能，且對氣動參數的攝動表現出了較強的魯棒性。