基于數值虛擬飛行的自旋尾翼鴨式布局彈箭動態氣動特性研究
龐川博,蔣勝矩,趙 超
(1 西安現代控制技術研究所,西安 710065;2 中國航空工業集團公司西安飛行自動控制研究所,西安 710065)
0 引言
鴨式布局是戰術導彈以及小型制導火箭彈最常用的氣動布局形式之一,由于舵面面積小、控制力臂長,因此具有響應快、操控效率高、鉸鏈力矩小等優點;舵機常布置于彈體頭部附近,有利于艙內組件的排布。當鴨舵舵面作滾轉控制時,其產生的不對稱洗流作用于尾翼上將誘導出反向滾轉力矩,使得舵面產生的滾轉控制力矩顯著降低,在工程應用上通常被認為不能有效進行滾轉控制。為了探索鴨舵控制時洗流的作用規律,國內外學者采用風洞試驗或數值模擬的方法開展了大量的工作,提出了一系列有效的措施來改善鴨式布局的滾轉控制效率[1-3],其中自旋尾翼是一種有效的途徑,通過將尾翼套筒用軸承連接于彈身上,使得尾翼上誘導產生的滾轉力矩與彈身解耦,從而達到滾轉可控的目的。國外學者早在20世紀70年代起就開展了一系列針對自旋尾翼的風洞試驗,對其控制效率和超聲速氣動特性進行了研究[4-5];國內雷娟棉[6]、張曉旻[7]等也通過風洞試驗證實了自旋尾翼作為滾轉控制改善措施的有效性。在數值計算方面,Blades[8]采用非結構網格對自旋尾翼流場進行了模擬;余奇華[9]等采用滑移網格研究了自旋尾翼在固定轉速下對導彈氣動特性的影響;Chen[10]等人研究了舵片固定偏轉條件下自旋尾翼的運動狀態以及繞流場分布;Liu[11]等人給出了自旋尾翼鴨式彈箭滾轉操控力矩的估算方法,并通過風洞試驗進行驗證。目前圍繞當鴨舵作實時滾轉控制時,含自旋尾翼的鴨式布局彈箭的動態氣動特性與控制特性所開展的研究還較少。
考慮到鴨式布局彈箭作滾轉機動時具有舵片偏轉頻率高、彈體姿態響應快的特點,同時彈身與自旋尾翼還具有雙旋運動的特征,采用數值虛擬飛行技術實現上述復雜運動的流場模擬是一種相對較好的手段。有別于靜態常規測力風洞試驗或定常氣動數值計算僅能獲取某固定狀態下局部線化的氣動力系數和導數,數值虛擬飛行技術通過實時耦合求解彈體氣動載荷/運動狀態/操縱面指令,能夠最大化還原機動飛行過程中非定常、非線性的流動現象。經過近20年CFD理論與計算機硬件的快速發展,西方先進國家在虛擬飛行動態數值模擬技術上已取得了較大的進展[12-14],國內相關單位和學者也開展了大量的研究[15-19],但更多是針對無控運動或開環控制過程。近年陶洋[20]等對方形截面導彈縱向運動進行了研究,在雙時間步內采用配平算法進行反饋控制,實現了導彈縱向姿態保持與變攻角機動過程的模擬;席柯、黃宇[21-22]等人在非定常求解器基礎上加入了六自由度運動模塊與PID閉環控制率模塊,使機動過程的模擬更接近于真實飛行過程;常興華、Zhang[23-24]等人對導彈姿態角控制過程、過載控制過程以及變馬赫數條件下的控制過程進行了數值模擬,得到的結果與試驗一致性較好,并在此基礎上開展了高機動導彈的控制率設計研究。文中基于動態嵌套網格流場求解器,發展了耦合求解動力、運動、閉環舵偏控制的一體化數值模擬手段,對鴨式布局彈箭尾翼自旋/固定時滾轉機動特性進行數值模擬,并對其彈體動態氣動特性與控制特性展開討論。
1 一體化數值模擬方法
1.1 流動控制方程
將三維非定常可壓縮NS方程寫為如下形式:
(1)
式中:Ω為控制體;?Ω為單位控制體邊界表面積;n為積分面的單位法向矢量;Q為守恒形式的狀態變量;F(Q)與G(Q)分別為對流項通量、粘性項通量。采用適用于非結構網格的二階有限體積法求解流場,時間推進采用隱式雙時間步方法。采用Menterk-ωSST湍流模型,其具體構造與特性見文獻[25]。為了提高計算效率,采用基于MPI的分塊網格并行技術。
1.2 6DOF運動求解
運動過程中計算模型的姿態、位置的變化通過求解其動力學方程組與運動學方程組得到,在慣性系下,計算模型質心的平動動力學方程組可寫成
(2)
式中:m為質量;V為模型質心的速度矢量;Pe為模型受到的合外力,無動力條件下通常為氣動力和重力。在跟隨模型運動的動坐標系下,其轉動動力學方程為:
(3)
式中:模型所受合力矩為M;其慣性矩張量矩陣為L;轉動角速度為ω。在已有當前時刻氣動載荷的前提下,求解式(2)~式(3)得到當前的加速度與角加速度,再通過以下運動方程組求解得到計算模型的線位移與歐拉角。
(4)
式(4)中線速度與線位移均在慣性坐標系中進行描述,而角速度在當前計算模型運動坐標系中進行描述。歐拉角則用于在慣性系下描述當前時刻計算模型的姿態,滿足x-y-z順規。在進行無控自由飛模擬時,隨時間推進依次交替求解式(1)與式(2)、式(3)、式(4)即可得到當前時刻計算模型的氣動載荷、繞流場分布以及運動狀態。當計算模型同時包含彈身與可動操縱面時,操縱面與彈身還具有相對角運動,需當作相互獨立的部件進行運動學計算,不同的部件保留各自的運動中心以及各自當地的隨體動坐標系,在跟隨彈身運動時,還需要依次單獨求解操縱面的運動。以鴨舵舵面為例,為便于描述其偏轉狀態,其轉動中心被設置在舵根部轉軸處,舵隨體坐標系原點與轉動中心重合,在初始時刻3個坐標軸方向與慣性系一致,首先在舵坐標系下寫出彈體當前時刻的角速度,可得到:
(5)
式中:Rx,Ry,Rz為基于當前時刻彈體歐拉角的旋轉矩陣;Rx′,Ry′,Rz′為基于當前時刻舵面歐拉角的旋轉矩陣,上標b與f分別表示矢量在彈體動坐標系或舵動坐標系下進行描述。考慮到通過旋轉矩陣與歐拉角來描述參考系旋轉需要進行多次矩陣運算與三角函數運算,計算效率較低且內存占用較大,此處采用四元數來描述不同坐標系間的相對位置關系,式(5)可重新寫為:
(6)
式中:qb與qf分別為描述當前時刻彈體姿態和舵片姿態的四元數,符號*表示四元數的矢量乘法,式(6)可得到在舵坐標系下因彈身轉動而牽連產生的角速度,在啟控過程中,舵片的合角速度可寫作:
(7)
(8)

(9)
同時也可以得到下一時刻描述舵片姿態的四元數:
qf_next=qf*dq
(10)
式(6)~式(10)可用于計算在考慮彈身運動時舵片姿態的變化。由于舵片啟控時僅進行轉動運動,其位置的變化完全由彈身的牽連運動產生,在慣性系下,時間步推進一步時彈體因角運動產生的角位移為:
(11)
其中ωi表示在慣性系下描述彈體角速度,采用類似式(6)的方式將彈體系下角速度轉換至慣性系下即可。同理,將慣性系下角位移增量dAi寫成四元數的表達形式qr后,存在如下關系:
(12)
lg與lg_pre分別表示當前時刻與上一時刻彈體質心到舵軸中心的矢徑,彈體平動產生的牽連線速度和線位移分別為vi和li,舵片由彈身轉動引起的總線位移ltotal和總線速度vtotal可寫為:
(13)
1.3 控制系統求解
(14)
令KI=KP/TI,KD=KP·TD,則KP、KI、KD分別為PID控制器中的比例系數、積分系數與微分系數。以單通道姿態控制為例,e(t)為當前姿態角與目標姿態角的偏差量,c(t)為控制器輸出的控制量,對于小尺寸制導火箭彈的滾轉控制,控制量與目標舵偏角r(t)可以寫成如式(15)所示關系。
(15)
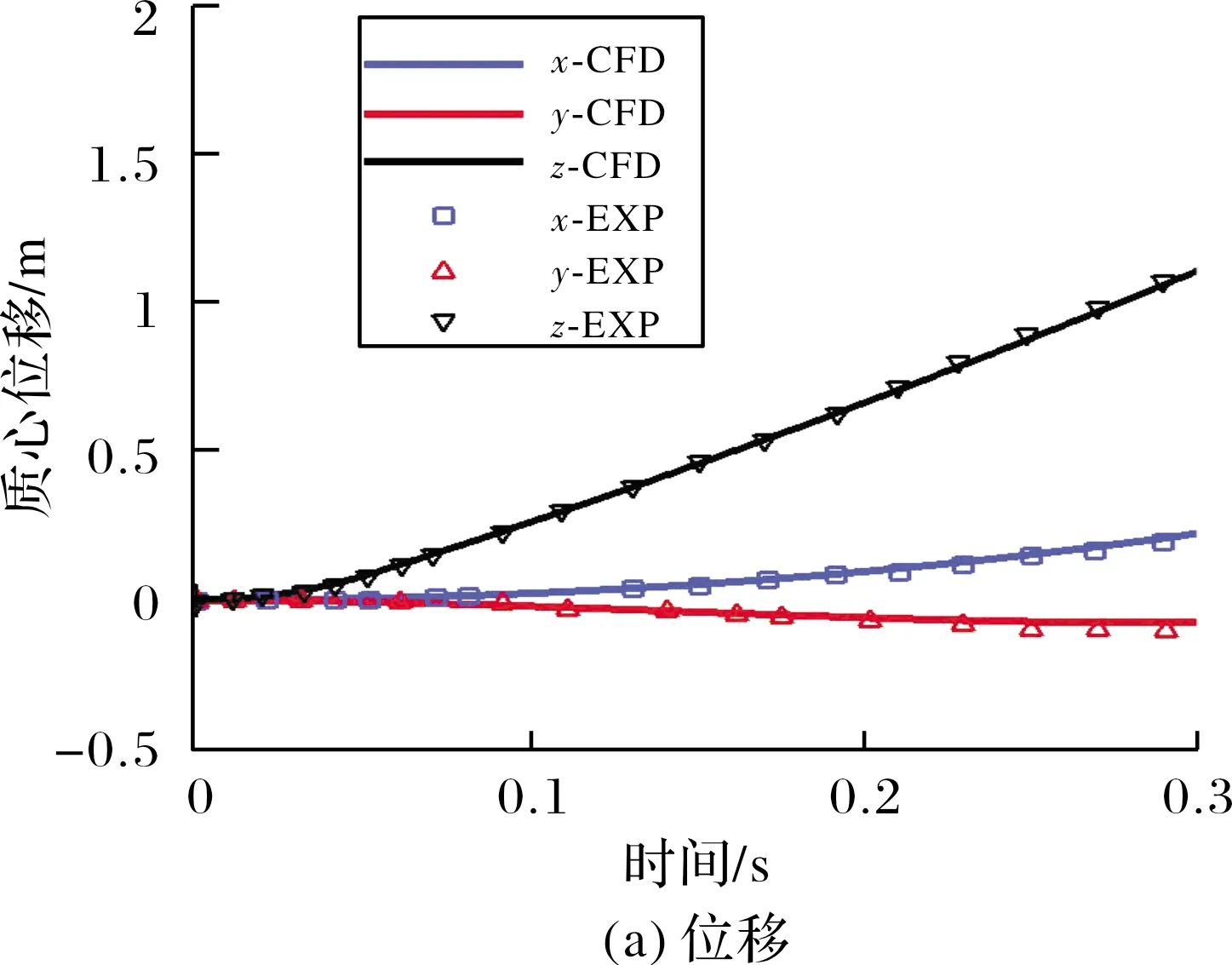
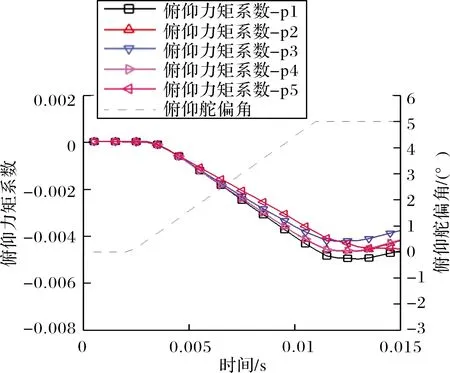
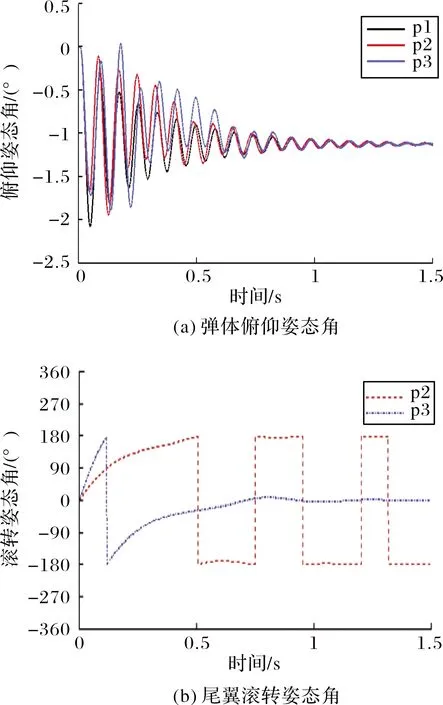
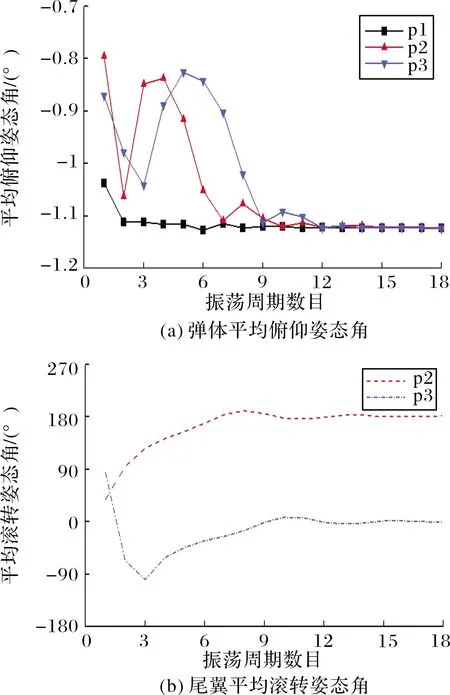
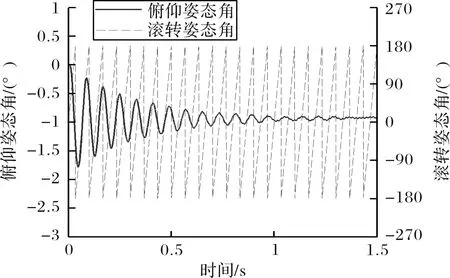
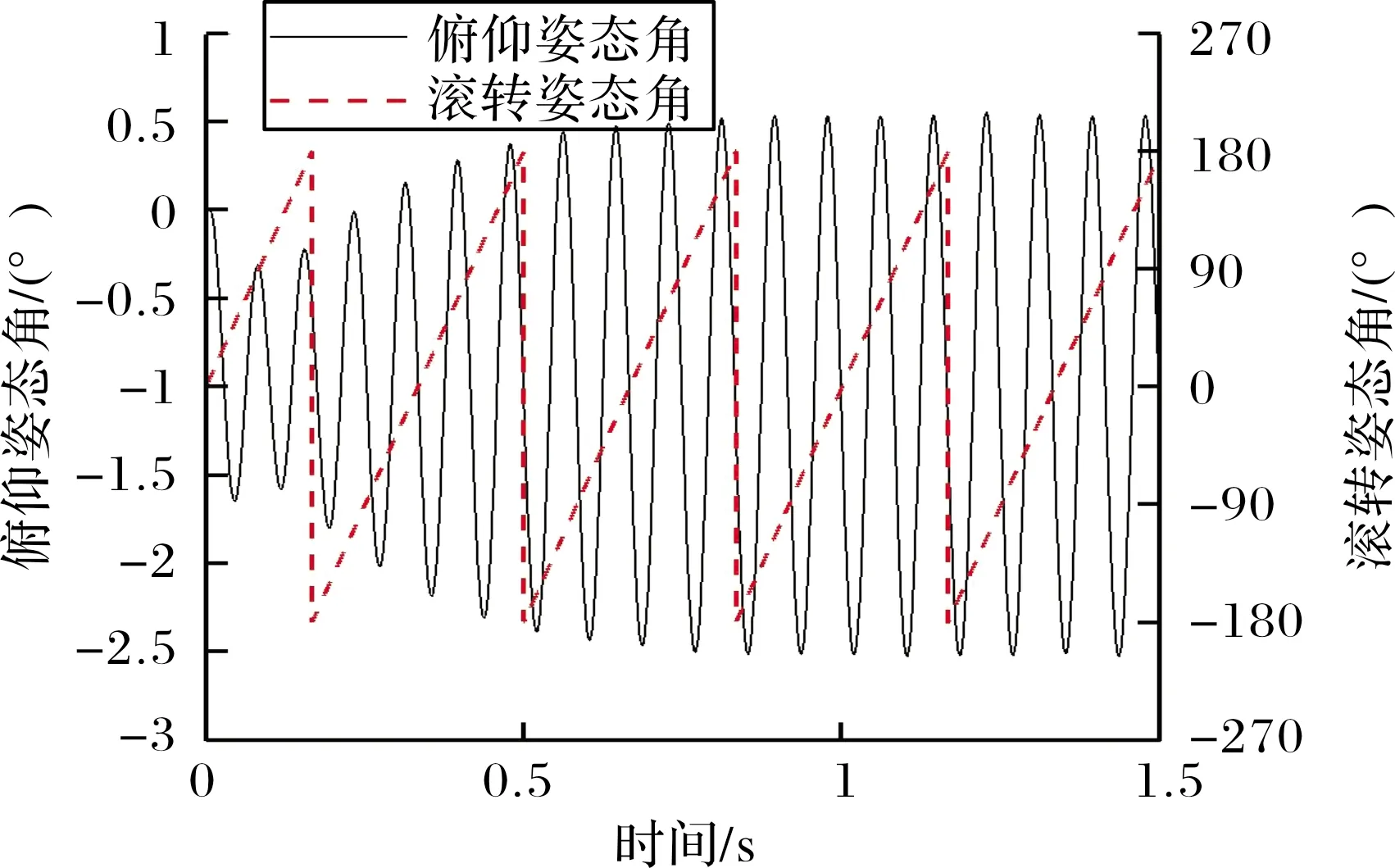
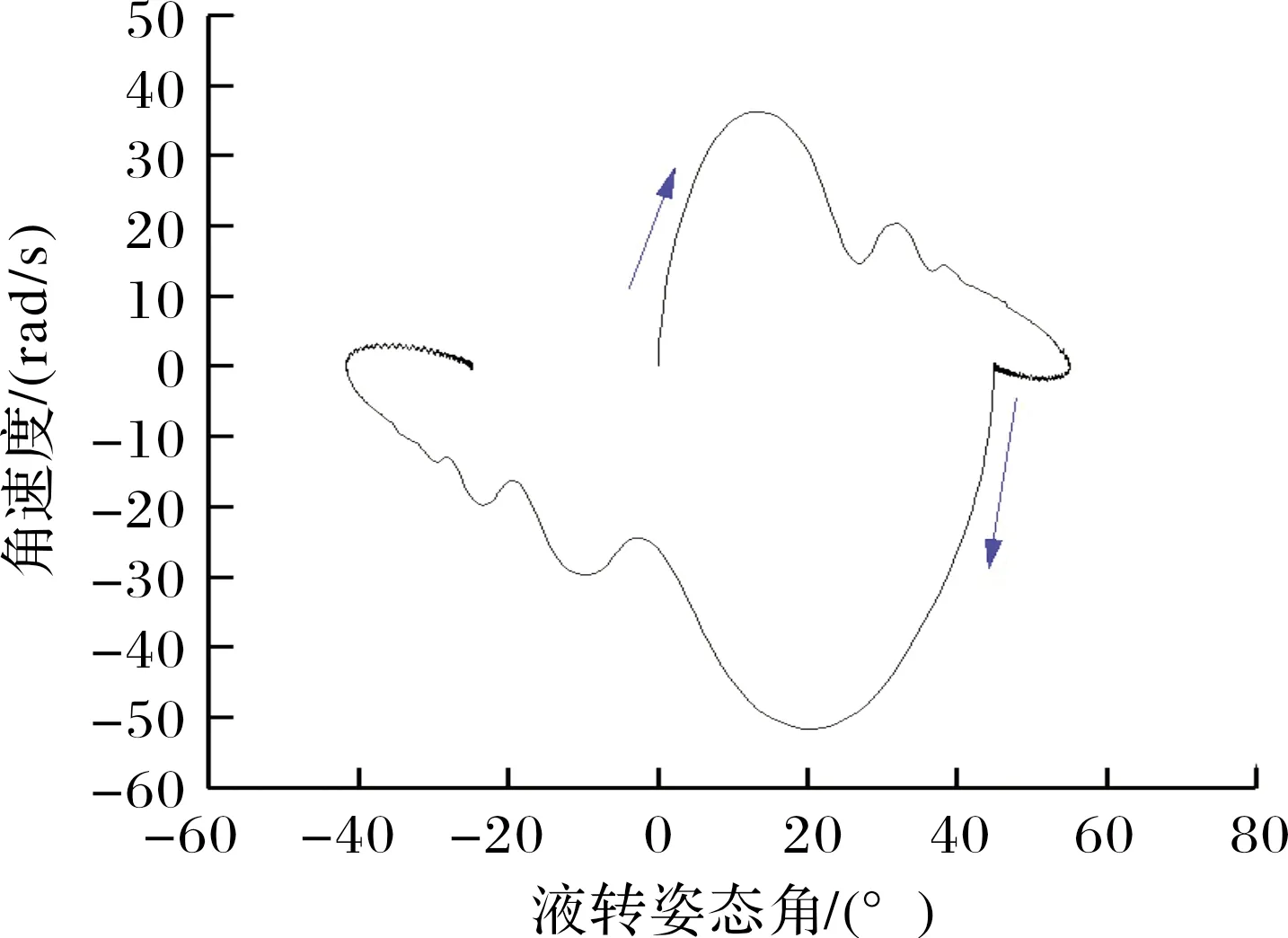
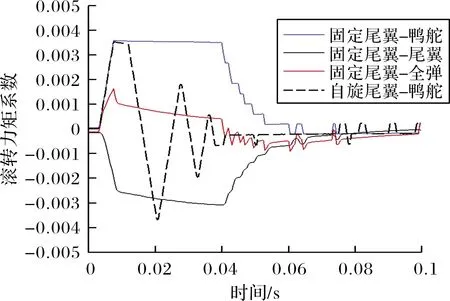
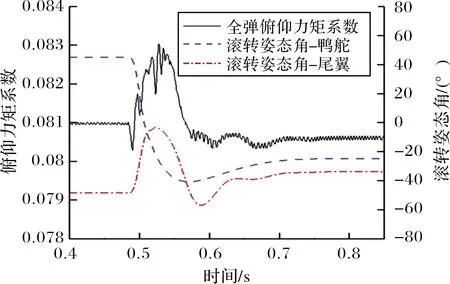
Fmax為通道舵偏角最大限幅。小尺寸制導火箭彈極轉動慣量往往很小,彈體滾轉響應速度快,加之滾轉控制系統屬于中立穩定系統,通過限幅可以有效避免滾轉角變化率超過舵片的轉動速率,有利于增強控制系統穩定性。由于舵片偏轉角速度由舵機自身能力決定,且舵機響應時間通常大于流動求解非定常時間步長,舵機在兩次接收控制信號之間依然沿用上一次的控制指令,在一次舵機響應時間間隔內,舵片偏轉運動角位移始終保持連續且角速率保持一致,更加符合真實運動過程。當計算時刻t滿足tst+nT≤t (16) 當目標舵偏角為零或達到設定的限幅時,式(16)右側為零。耦合閉環控制系統的六自由度運動非定常流場求解過程分為以下步驟:1)通過定常方法求解初始狀態下的流場;2)以定常流場為初始條件開展非定常計算,得到時間步推進一步時彈體所受非定常氣動載荷;3)控制系統根據當前彈體姿態解算目標舵偏角,得到當前時刻舵片的控制偏轉角速度;4)根據當前氣動載荷計算得到彈體的線加速度與角加速度;5)根據步驟3~步驟4計算得到當前時刻彈體與舵片的姿態與線位移,更新全彈的姿態和位置,更新計算網格;6)推進時間步,求解更新后網格的非定常流場。重復步驟3~步驟6,直至計算結束。 通過模擬典型外掛物投放的運動過程來驗證文中非定常流場計算模塊與運動模塊耦合求解的正確性。計算模型由機翼、掛架與外掛物組成,其外形如圖1所示。 圖1 機翼-外掛物模型 該外形多次用于嵌套網格與動態運動過程的驗證[18,23],模型尺寸、來流條件參考文獻[26]。采用非結構網格對計算域進行空間離散,在外掛物掉落途經區域加密背景體網格,在機翼、外掛物的前后緣同樣進行加密,物面邊界層網格以棱柱網格為主,底層高度為1×10-5m。通過計算,得到外掛物分離掉落后質心位置改變隨時間變化的曲線如圖2(a)所示,歐拉角曲線如圖2(b)所示,線速度與角速度隨時間變化的曲線如圖2(c)與圖2(d)所示。對比計算結果與試驗值可知,文中采用的耦合計算方法在求解物體運動過程中非定常流場時能夠取得較好的效果。 圖2 CFD結果與試驗結果對比 采用的研究模型為典型鴨式布局導彈,外形如圖3所示。彈身由頭部錐段與圓柱段組成,長徑比L/D=11.2,在頭錐后布置有4片鴨舵,彈尾處布置有4片尾翼,在初始狀態時舵、翼方位呈“++”狀態,舵尾間距為7.75D。計算模型忽略舵軸的影響,鴨舵底部與彈身之間縫隙距離為0.059D,旋轉尾翼所在的圓柱形套筒的軸向長度為1.2D,為保證計算過程中物面邊界間互不干涉,套筒與彈身圓柱段留有微小的縫隙,縫隙距離為0.000 3D。 圖3 鴨式布局導彈示意圖 流場空間采用非結構嵌套網格進行離散,具體如圖4所示,彈身、4片鴨舵以及旋轉尾翼獨立生成計算網格,同時彈身網格也當作背景網格。不同部件間網格存在重疊或嵌套的關系,流場信息在部件網格重疊區域通過插值進行傳遞,部件之間存在相對運動時網格不進行變形,具有魯棒性好、使用方便的優點。計算域呈圓柱形,上游到彈頭距離為12L,下游距離彈尾14L,遠場邊界距彈軸11L,邊界層第一層高度為3×10-5L。 圖4 鴨式布局導彈嵌套網格示意圖 含自旋尾翼的鴨式布局火箭彈在飛行過程中尾翼處于自由旋轉狀態,當受到不對稱來流擾動時,自旋尾翼處于轉動狀態,此時作俯仰機動控制,旋轉尾翼將受到鴨舵洗流的作用。取來流馬赫數Ma=3.0,雷諾數Re=6.98×107,溫度Tref=288.15 K,將鴨舵呈俯仰5°舵偏角放置,尾翼自旋角速度固定為3 r/s與6 r/s,彈體相對來流呈0°攻角且姿態保持固定,取非定常時間步長Δt=5×10-4s。在[-180°,180°]區間內表示彈體滾轉姿態角,給出旋轉尾翼的姿態與受力變化,如圖5所示,在洗流的作用下,尾翼受到向下的法向力且隨尾翼自旋呈周期性變化,初始時刻法向力的值最大,洗流作用最顯著,此時尾翼姿態為“十”型;當其轉過45°后變為“X”型后,法向力值達到最小,說明此時洗流強度最小。尾翼以較低的角速度旋轉時,自旋一周對應其俯仰方向洗流強弱交替周期變化4次,且法向力的變化僅與當前尾翼所處相位角相關,自旋角速度的大小對其受洗流強度幾乎無影響。 圖5 旋轉尾翼姿態與所受法向力 繼續研究在尾翼自由旋轉的狀態下,彈體作俯仰操控時全彈的俯仰姿態響應變化。舵片偏轉速度設為10 rad/s,預設的俯仰舵偏規律如下: 其中首次啟控時刻tst=0.002 s,當非定常計算時間大于啟控時刻時,舵片開始按預設規律偏轉,直至達到目標舵偏角。由于舵片偏轉速度很大,舵偏角變化規律近似于階躍型函數。尾翼運動狀態分為固定不旋轉、賦初始轉速自由旋轉與固定轉速旋轉3類,如表1所示。 表1 計算工況 w0為非定常計算開始時刻尾翼初始轉速,旋轉尾翼無幾何賦旋特征時,其旋轉狀態受控制引起的洗流影響以及飛行中擾動的作用呈低速微旋狀態,3 r/s符合多數小型傾斜穩定火箭彈受到較大擾動時彈體的轉速,以此轉速為尾翼旋轉的角速度具有一定實際意義;當尾翼具有斜切或斜置等賦旋特征時,在一定飛行速度下其以較固定的轉速旋轉,此處以尾翼定轉速旋轉來進行模擬。來流狀態與上文保持一致,首先求解定常流場直至流動穩定,并以此為初場進行非定常計算,t=0 s時刻尾翼按文中設定條件開始運動。舵翼作俯仰偏轉運動時彈體俯仰力矩變化如圖6所示,在剛開始啟控后2~3 ms內,舵片上立即產生正向的法向力,由于尾翼上的洗流效應不明顯,不同工況下全彈俯仰力矩變化也較為一致。隨時間推進,鴨舵產生的下洗流動逐漸作用于彈身及尾翼上,彈體與舵翼、尾翼翼面產生的合力矩即為當前時刻操控力矩與恢復力矩之和,在計算初期,彈體俯仰姿態變化極小,可忽略彈體產生的恢復力矩,此時給出的彈體俯仰力矩可認為是該段時間內的操控力矩。t=0.012 s時刻,舵片已達到預設偏轉角,由于工況p1尾翼始終固定為“十”型姿態,受洗流影響最大,全彈俯仰操控力矩最大;工況p2和工況p4此時尾翼所處相位接近,所受操控力矩也接近;工況p3尾翼自旋角速度較大,尾翼相位姿態更加接近于“X”型姿態,所受俯仰操控力矩最小;工況p5的尾翼自旋角速度最大,首次操控力矩最大值出現在t=0.0145 s附近,受洗流作用影響的時間明顯滯后于其他工況,說明轉速越高,旋轉尾翼對洗流作用的響應時間越長。 圖6 彈體俯仰力矩與舵偏角變化 尾翼固定與自由旋轉時全彈姿態角變化曲線如圖7所示,在空氣阻尼的影響下,尾翼自由旋轉最終轉過的角度大約為180°與360°(對應初始轉速3 r/s與6 r/s)。從工況p1可知,當前馬赫數下彈體的俯仰振蕩周期約為82.2 ms,當尾翼以低轉速旋轉時,3種工況俯仰振蕩周期差別不大,且隨尾翼旋轉角速度降低而趨于一致;并且工況p2與p3每次俯仰振蕩的中值(平均俯仰姿態角)更小,將工況p1,p2,p3的姿態角按俯仰振蕩周期進行平均后得到如圖8所示的曲線。 圖7 固定尾翼與自旋尾翼條件下彈體姿態角 圖8 每個俯仰運動周期的平均姿態角 圖8中橫軸表示俯仰振蕩周期數目,其中工況p1尾翼固定,其滾轉姿態角始終為0°,此時洗流影響最大,相應俯仰操控力矩也最大,故其俯仰姿態角的周期均值基本保持一致;工況p2與p3在一個振蕩周期內的俯仰姿態角均值與當前周期的平均滾轉角相關,當該周期的平均滾轉角越接近0°,90°,180°,即尾翼姿態越接近“十”型時,對應操控力矩越大,俯仰姿態角均值也越大。隨著時間進一步推進,受阻尼影響俯仰振蕩振幅逐步減小,自旋尾翼的角速度也降低至零,此時3種工況的尾翼相位姿態基本一致,俯仰姿態角也逐漸趨于一致。 在工況p5中,尾翼以較高轉速定速旋轉,其姿態角隨時間的曲線如圖9所示,全彈俯仰角依然呈振蕩收斂趨勢,其振蕩周期約為80.8 ms,最終收斂的俯仰平衡狀態約為-0.93°,與工況p1對比可知,尾翼以較高角速度定速自旋對俯仰振蕩周期或頻率影響很小,但由于尾翼姿態在“十”型、“X”型之間反復變化,受洗流的作用強度降低,綜合俯仰控制能力更弱,最終能達到的平衡俯仰角更小。通過分析,尾翼作定速旋轉運動時,其俯仰方向受力與力矩隨轉動呈周期性變化,且在當前來流速度下,尾翼自旋一周,其受到的法向力周期變化4次,當洗流強度變化周期與俯仰振蕩周期接近,即尾翼自旋周期為彈體俯仰振蕩周期的4倍左右時,會產生類似共振的現象,此時彈體姿態受定速旋轉尾翼上的交變氣動載荷的影響,全彈俯仰角將在平衡位置附近來回振蕩。工況p4下全彈滾轉姿態角與俯仰姿態角的變化曲線如圖10所示,可知在尾翼自旋經過3個周期后全彈俯仰振蕩最大幅值與振蕩頻率值趨于穩定,此時彈體在俯仰角-1.013°附近、以振幅約1.5°進行俯仰振蕩。 圖9 工況p5條件下的姿態角 圖10 工況p4條件下的姿態角 討論了自旋尾翼對火箭彈俯仰動態特性的影響,下面對其滾轉控制特性以及滾轉操控過程中對縱向氣動特性的影響進行分析。預先設定的彈體滾轉姿態角變化要求為:非定常計算開始后經過2 ms啟動控制,要求彈體沿x軸正向轉動45°后并保持該姿態角,姿態穩定一段時間后,將彈體滾轉姿態角控制至-25°,保持該姿態直至計算結束。 不同于俯仰機動,在作滾轉控制時4片鴨舵都將進行偏轉,非定常模擬時僅釋放彈體滾轉方向的自由度,鴨舵與尾翼在計算初始時刻相對攻角平面均處于“++”方位,旋轉尾翼初始角速度為零,來流條件保持與第3節中一致。首先模擬零攻角狀態下含自旋尾翼的鴨式布局火箭彈滾轉控制過程,給出了彈體滾轉姿態角的響應曲線以及滾轉角速度相對滾轉姿態角的相圖,如圖11(a)所示,2次滾轉姿態控制過程均較快速且穩定,控制超調量約為22%,姿態過渡時間約為0.3 s,姿態振蕩次數小于1次,計算滾轉通道舵偏角限幅Fmax=2.5°。如圖11(b)與圖12所示,當前限幅條件下彈體響應速度仍相當快,2次姿態控制過程中彈體的轉動角速度均遠遠超過了舵片的偏轉角速度,機動過程中控制模塊需要反復給出反向舵偏指令來對彈體滾轉角速度進行控制,使超調量不至于過大從而避免控制發散,也反映出采用旋轉尾翼后鴨舵控制能力較強的特點。達到控制目標后,彈體處于姿態保持階段,由于彈體在滾轉方向為中立穩定系統,為了抵消由空間離散與數值方法引起的擾動對姿態的影響,控制模塊依據彈體受力的變化仍不斷給出控制指令,舵片按要求進行反復小幅度的偏轉來保持所要求的姿態。 圖11 自旋尾翼條件下舵偏角及彈體姿態 圖12 自旋尾翼條件下角速度隨滾轉姿態角變化曲線 為了直觀對比自由旋轉尾翼對提高控制效率的作用,將模型的旋轉尾翼改為“十”型布置的固定尾翼,在相同來流條件下,保持控制參數一致,進行從滾轉姿態角0°至45°的姿態控制,滾轉舵偏限幅仍設為Fmax=2.5°,得到滾轉姿態角、舵偏角隨時間的變化曲線以及彈體滾轉角速度隨滾轉姿態角變化的曲線。 如圖13所示,固定尾翼條件下實現鴨舵滾轉控制的姿態過渡時間與旋轉尾翼工況接近,但在姿態變化啟動過程中所使用到的平均滾轉舵偏角顯然更大,舵控時間也更長,在t為0~0.05 s時滾轉舵偏角始終處于最大限幅狀態,超調量約為33%,大于文中旋轉尾翼工況的超調量,且在姿態保持階段(t>0.3 s)用到的滾轉舵偏角也更大。以圖14可知,在舵控時間增長、平均舵偏角更大的前提下,彈體最大角速度僅約為22 rad/s,小于旋轉尾翼工況時的36 rad/s。以上現象均說明在尾翼固定情況下鴨舵的滾轉控制能力大幅減弱,給出滾轉控制前期鴨舵與尾翼的滾轉力矩系數變化曲線如圖15所示,圖中分別給出尾翼固定和尾翼自由旋轉兩種條件下彈體各部件的滾轉力矩,可知二者在鴨舵上能夠產生的最大滾轉力矩一致,但尾翼固定時在尾翼上會產生顯著的反向誘導力矩,t=0.01 s時自旋尾翼工況的滾轉控制能力約為固定尾翼工況的3.5倍,隨著彈體轉速加快,固定尾翼上的反向誘導力矩逐步增大,在t=0.04 s時誘導力矩大小可達到鴨舵控制力矩的88%,合滾轉力矩僅為鴨舵控制力矩的12%,此時滾轉控制能力僅是自旋尾翼工況的1/9。 圖13 固定尾翼條件下舵偏角及彈體姿態隨時間變化曲線 圖14 固定尾翼條件下角速度隨滾轉姿態角變化曲線 圖15 不同部件的滾轉力矩隨時間變化 由此可知,當采用固定尾翼時,盡管在當前來流狀態下能夠實現鴨舵滾轉控制,但實際控制能力已經遠小于同樣外形自由旋轉尾翼的工況,當舵翼尺寸進一步減小、彈體轉動慣量增大或降低滾轉舵偏限幅時,彈體滾轉控制能力進一步減弱,尾翼固定與自旋尾翼所引起的滾轉控制效率的差異將會更大。 在小攻角狀態下,討論自旋尾翼彈箭滾轉機動過程中俯仰方向氣動特性變化。計算來流攻角取α=4°,其余來流狀態、計算條件以及姿態控制條件均保持與文中含自旋尾翼工況所描述一致,取非定常計算的前0.06 s(對應第一次滾轉姿態控制的舵控時間段),給出來流有/無攻角時彈體的滾轉舵偏角曲線與滾轉力矩曲線。 如圖16所示,小攻角條件下,來流攻角對滾轉操控特性影響較小,在采用相同控制參數時,兩種工況均先給出限幅條件下最大舵偏指令,持續30 ms后又同時給出了反向舵偏指令來抑制彈體轉動速度,由圖中力矩曲線可知,在相同舵偏角條件下來流有攻角時將產生略微更大的滾轉操控力矩,從而在t=0.02 s附近給出抑制彈體滾轉角速度的反向舵偏指令持續時間更長,也使得后續時間里舵片的大幅偏轉次數更多。 圖16 滾轉舵偏角與滾轉力矩隨時間變化 圖17中給出了小攻角下第二次滾轉姿態控制階段(滾轉角從45°變化至-25°)全彈的俯仰力矩變化曲線,同時也給出了尾翼和鴨舵的滾轉姿態角,此時鴨舵僅進行滾轉控制,彈體的俯仰力矩可認為是驅使姿態恢復至平衡狀態的恢復力矩。如圖17所示,盡管控制過程中尾翼與鴨舵的相位姿態、轉動角速度、以及鴨舵舵偏角均出現較大的變化,全彈俯仰力矩改變量仍然較小(不超過3%),且在控制前后的姿態維持階段(圖中t>0.8 s以及t<0.48 s)全彈的俯仰力矩改變量小于1%,說明自旋尾翼在滾轉控制過程中,其相位、角速度所發生的變化對全彈縱向氣動特性影響十分有限。 圖17 全彈俯仰力矩與舵、翼滾轉姿態角隨時間變化 通過耦合求解流動控制方程、動力學方程與飛行控制率,對含自旋尾翼的鴨式布局彈箭進行了數值模擬,重點關注其俯仰動態特性與滾轉姿態操控特性,通過對氣動載荷、運動姿態進行分析,得出以下結論: 1)尾翼旋轉時,鴨舵誘發的洗流作用效果呈周期性變化,對于中等長細比彈箭在小攻角條件下,洗流作用效果僅與當前尾翼的相位姿態相關,當尾翼姿態呈“十”型時洗流效果最明顯,尾翼自旋角速度大小對其受洗流作用強度基本無影響。 2)彈體俯仰機動過程中,自旋尾翼旋轉角速度越大,鴨舵產生洗流作用于尾翼的時刻更加滯后;尾翼以不同初始轉速自由旋轉時,不影響彈體作俯仰機動后俯仰振蕩收斂所需的時間與最終達到的平衡角度,僅在振蕩過程中因尾翼相位姿態角不同而引起瞬時操縱力矩不同,進而俯仰振蕩幅值與均值出現差異。尾翼定速旋轉時,較高的轉速使得縱向洗流效果減弱,俯仰控制能力降低,當定速旋轉周期接近振蕩周期的4倍時,會產生類似共振的現象,此時彈體會在平衡位置附近進行俯仰振蕩。 3)所采用的數值虛擬飛行技術能夠較好模擬彈箭滾轉姿態閉環控制過程。通過比較尾翼固定與自由旋轉彈體作滾轉機動時的力矩變化,尾翼固定時的滾轉操控能力大幅降低;在小攻角條件下,攻角變化對自旋尾翼彈箭滾轉操控能力影響不明顯,在滾轉控制過程中,自旋尾翼姿態的變化對全彈縱向氣動特性影響較小。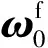
2 數值方法驗證

3 縱向氣動特性研究




4 滾轉控制動態特性研究




5 結論

