基于深度神經網絡的電力變壓器故障診斷
鄧燕山, 趙凱利, 呂文超, 白杰, 董杰, 高嶺
(國網冀北電力有限公司唐山供電公司, 河北 唐山 063000)
0 引言
溶解氣體分析法(DGA)是診斷電力變壓器故障的常見方法[1]。DGA的原理是故障電力變壓器在熱應力和電應力作用下,其油紙絕緣層會分解出可溶解的氣體,通過氣體分析可以診斷變壓器的故障類型[2]。本文將使用深度神經網絡算法(DNN)對溶解氣體數據進行挖掘分析,以實現變壓器故障的自動分類。
DNN需要大量數據進行監督學習。為了降低對高可用性數據的依賴,本研究將使用杜瓦爾三角法生成模擬DGA數據,并將其應用于DNN訓練中。為了證明DNN在電力變壓器故障診斷應用中的有效性和性能,本文針對分類準確性將DNN與隨機森林分類算法(RFC)、K最近鄰分類算法(KNN)進行了對比測試。
1 機器學習算法
1.1 KNN算法
KNN算法是簡單的且廣泛使用的監督聚類算法之一。其主要思想是通過數據點之間距離的計算,實現對未分類的數據進行分類。k是最近數據點的數量。對于每個未分類的點,該算法將計算其與k個最近的數據點之間的距離,如圖1所示。
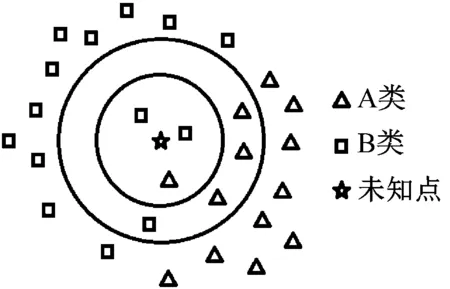
圖1 KNN算法
如果k設置為3,則未知點將歸為B類,因為三個最近點中的兩個屬于B類;如果k設置為7,則未知點將屬于A類,因為屬于A類的點最近。
KNN算法通常會產生一致的結果,并且計算過程較簡單[3]。但是,該算法的效率會隨著數據量的增大而大幅下降[4]。
1.2 隨機森林分類算法(RFC)
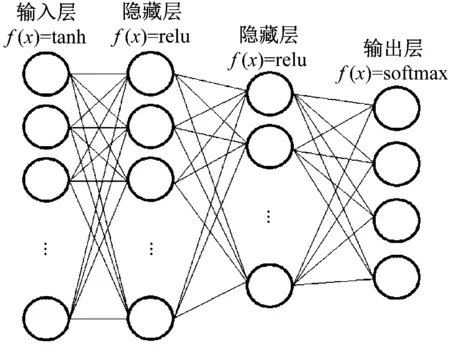
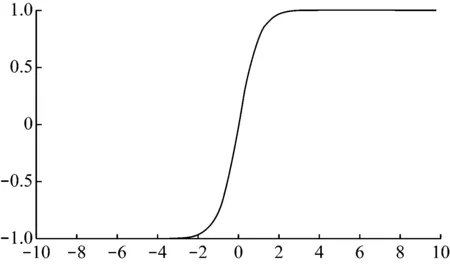
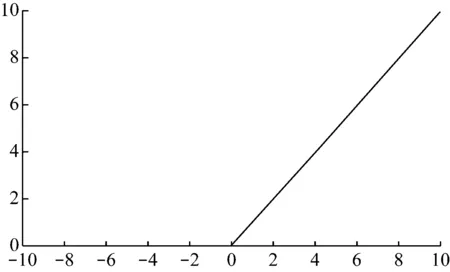
RFC是一種監督聚類算法。該分類算法由多個決策樹組成,這些決策樹用于對未分類的數據集進行分類。每個決策樹都是一個分類器。如果有N個訓練數據,則在訓練過程中,隨機替換M個訓練數據(M 神經網絡是從生物神經元結構衍生而來的抽象和簡化模型。通常,神經網絡模型由輸入層、隱藏層和輸出層組成。每層中的節點都模仿神經元,節點之間使用不同的權重進行連接[7]。 神經網絡算法的過程包括輸入數據正向傳播和誤差反向傳播。在正向傳播中,原始數據從輸入層傳輸到隱藏層,隱藏層使用激活函數提取數據的特征。激活函數的目的是通過加權輸入的非線性組合產生非線性決策邊界。輸出層完成分類過程[8]。在誤差反向傳播中,該算法利用監督的分類結果并修改神經元連接的權重[9]。 DNN由多個隱藏層組成,如圖2所示。 圖2 神經網絡 每個層都應提取不同級別的數據特征。分類器包含兩個隱藏層。輸入層的激活函數為tanh,兩個隱藏層的激活函數為ReLU,輸出層的激活功能為SoftMax。 tanh函數將實數值映射到[-1,1]范圍,如圖3所示。 圖3 tanh函數圖形 ReLU函數的計算式為f(x)=max(0,x),如圖4所示。 圖4 ReLU函數圖形 與tanh函數相比,ReLU函數的優點之一是極大地加快了隨機梯度下降的收斂速度[10]。因此,將兩個隱藏層的激活函數選擇為ReLU。Softmax(歸一化指數函數)函數[11]的計算式為式(1)。 (1) σ(z)是輸出向量,zj是輸入向量z的元素,如圖5所示。 圖5 Softmax函數圖形 在反向傳播過程中,本研究使用Adam優化方法更新網絡權重。相對于隨機梯度下降優化方法,Adam優化方法可以根據梯度的第一和第二矩的估計來計算不同參數的單獨學習率。經驗結果表明,Adam優化方法在實踐中比隨機梯度下降方法效果更好[12]。 常見的分析變壓器油中所溶解氣體的方法有關鍵氣體法、Rogers比率法、Doernenburg比率法和杜瓦爾三角法[13-14]。通過338個油樣的對比試驗表明,與其他溶解氣體分析方法相比,杜瓦爾三角方法具有最高的一致性。 因此,在本研究中隨機生成大量的氣體化合物百分比數據,并使用杜瓦爾三角法生成相應的故障類型。這些模擬數據分為用于深度神經網絡模型的訓練數據集和測試數據集。杜瓦爾三角分析法如圖6所示。 圖6 杜瓦爾三角 杜瓦爾三角故障區域如表1所示。 表1 杜瓦爾三角故障區 實驗首先是隨機生成包含三種氣體的數量的1 000個數據點的數據集,并使用杜瓦爾三角方法確定相應的故障類型。從故障變壓器歷史數據得出的最小值和最大值邊界,以確保所生成的數據樣本落在經驗值邊界之內。三種溶解氣體為CH4、C2H2和C2H4,它們各自的百分比為三種氣體占氣體總量的比例。由于某些故障類型的發生概率較低,本實驗將七種故障類型組合為五種:低能放電(D1和PD)、高能放電(D2)、最高700℃的發熱故障(T1、T2)、高于700℃發熱故障(T3)以及熱電故障(DT)。每個樣本的故障類型編碼都為0到4之間的整數,如表2所示。 表2 故障編碼 為了測試數據大小的影響,實驗采用生成的數據集的子集的方式來形成其他數據集。具體而言,創建分別具有350、700和1000個數據點的三個數據集。對于這三個數據集的每一個,將80%的數據點用作訓練數據集,并將其余的數據點(20%)用作測試數據集。實施的DNN模型的每一層中的節點數分別為256、126、32和5。實驗首先以10-3的學習率訓練網絡,然后將其更改為10-5進行測試。深度神經網絡的參數如表3所示。 表3 DNN參數 基于表3指定參數,深度神經網絡模型(DNN)在具有1 000個數據點的數據集上實現了99.68%的精度。實驗還使用相同的數據集測試了KNN和RFC。KNN算法的準確率為97%,而RFC為97.65%。 為了檢查數據大小對準確性的影響,實驗采用了三種不同大小的數據集,這三個實驗過程的準確性如表4所示。 表4 每種故障類型與整體精度的準確性比較 從表4可以看出,隨著數據點數量的增加,實驗的準確性都會提高。實驗結果可以總結如下:(1) 數據集越大,每種方法在電力變壓器故障識別應用中的總體精度就越高;(2) 測試結果表明,與KNN和RFC方法相比,DNN具有更高的識別準確性。 本文使用DNN來識別變壓器的故障類型。在本研究的實驗中隨機生成數據點,并使用杜瓦爾三角法確定用于監督學習的故障類型。DNN被設計為具有四層的網絡結構,其激活函數分別是Tanh、ReLU和SoftMax。權重更新使用Adam優化器。試驗結果表明,與KNN和RFC相比,DNN在識別變壓器故障類型方面具有更高的準確性。1.3 深度學習網絡
2 采用杜瓦爾三角生成仿真數據


3 實驗驗證

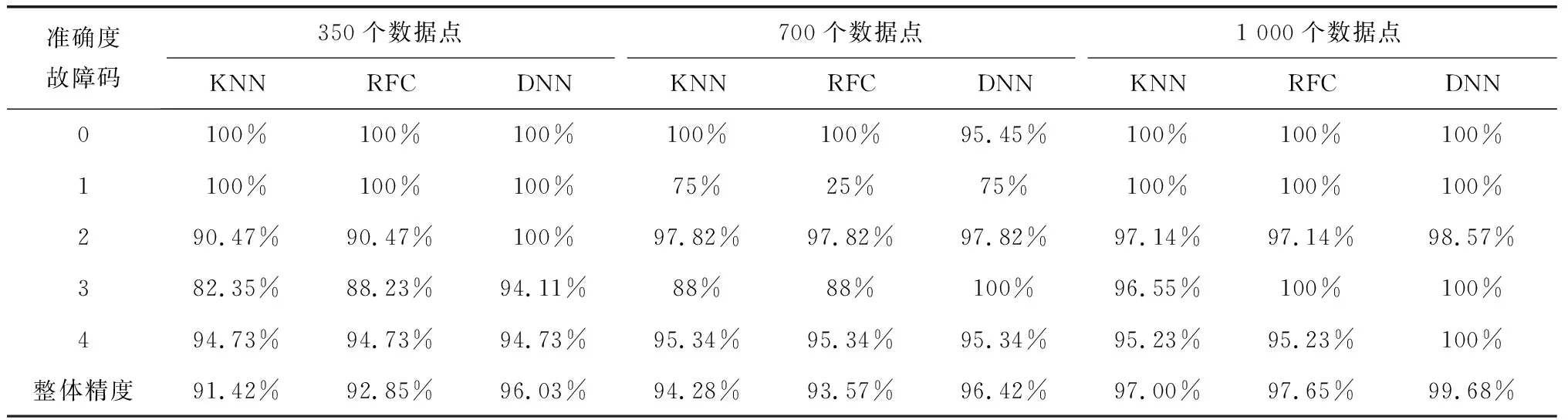
4 總結

